An official website of the United States government
 United States Department of Labor
United States Department of Labor

Crossref 0
Pragmatic clinical trials: Emerging challenges and new roles for statisticians, Clinical Trials, 2016.
Opportunities and barriers for pragmatic embedded trials: Triumphs and tribulations, Learning Health Systems, 2018.
A study using a large sample of agreements between sponsors of clinical trials and clinical investigators produces estimated hedonic price indexes for clinical trial research, an important component of biomedical research and development. Measured as total grant cost per patient, nominal prices grew by a factor of 4.5 between 1989 and 2011, while the U.S. National Institutes of Health Biomedical R&D Price Index, the only published source of information on trends in pricing in the biomedical research-and-development sector, rose only slightly more than twofold. After controlling for changes in the characteristics of clinical trials (e.g., average number of patients per site and “site work effort”), however, the estimated rate of inflation in clinical trials costs was found to track the Biomedical R&D Price Index quite closely, suggesting that it should be feasible for statistical agencies to develop a producer price index for biomedical research-and-development activities.
Expenditures for research and development (R&D) are widely acknowledged to a play a key role in economic growth and competitiveness, and statistics on R&D are closely watched as indicators of technological change and the nation’s economic performance.1 Yet R&D has historically been treated in the national accounts as a business expense, rather than as an investment in knowledge, a convention that has important implications for estimating GDP and its growth. As a first step in treating R&D as an investment component of GDP, the Bureau of Economic Analysis (BEA) has created an R&D satellite account, which reports that R&D contributed 20 basis points to the reestimated 2.9-percent average rate of U.S. real GDP growth from 1957 to 2007.2 But such calculations can be quite sensitive to the use of deflators, and the nature of R&D activities presents substantial price measurement challenges to statistical agencies. Although the Bureau of Labor Statistics (BLS) has steadily expanded the scope of its collection of price statistics on the service sector, it does not currently publish a producer price index (PPI) for business R&D services, a major component of total R&D activity in the United States.3 In experimenting with the satellite R&D accounts, BEA has utilized various proxy deflators to construct measures of real business R&D output, including cost-based aggregate indexes for inputs to R&D (that implicitly assume no productivity growth in R&D activities), weighted combinations of gross output prices of industries investing in R&D, and a variety of other next-best alternatives in lieu of actual R&D output prices.4 Were a broad-based PPI for contracted business R&D available, it could be used to develop estimates of real private sector R&D output by deflating a portion of the Census Bureau’s nominal expenditure estimates for NAICS 5417, “Scientific Research and Development Services.” As noted by BLS Assistant Commissioner David Friedman, however, what is desired is an ideal PPI “that directly measures actual market transactions for R&D output.”5
This article contributes to that broader effort by studying the measurement of R&D transactions prices for the specific area of biomedical clinical research. Biomedical research is the single biggest component of the R&D sector’s estimated contribution to growth: in the BEA’s initial estimates in the satellite account, biotechnology-related industries contributed 44 percent of the total business R&D contribution to real GDP growth between 1998 and 2007. Following biotechnology’s lead were information-, communications-, and technology-producing industries, with a 36-percent contribution; transportation equipment industries, with 11 percent; and all other industries, with 9 percent.6 Within biomedical research, clinical trials account for a large fraction of commercial R&D expenditures: of the $46.4 billion spent by Pharmaceutical Research and Manufacturers of America (PhRMA) member companies on R&D in 2010, $32.5 billion (70 percent) went toward clinical trials involving human subjects, with a much smaller proportion devoted to preclinical and basic research.7 In recent years, clinical research has accounted for about one-third of the total budget of the National Institutes of Health (NIH; e.g., $10.7 billion out of $30 billion in fiscal-year 2010), of which a substantial fraction ($3.2 billion that same year) went toward clinical trials.8
Clinical research is also an activity that has undergone considerable organizational, technological, and economic changes, with potentially important implications for productivity. Over the past three decades, the design and management of clinical trials has become increasingly sophisticated, and at the same time, the types of organizations conducting clinical trials have changed. Much of the effort expended by biopharmaceutical firms in running clinical trials is increasingly being outsourced to specialist entities called contract research organizations (CROs), rather than being carried out in-house or in direct collaborations with external academic medical center investigators.9 Moreover, within the United States, sponsors are moving trials away from academic medical centers toward physician practices, many of them for-profit practices.10 For example, although the number of clinical research contracts carried out annually by academic investigators remained relatively constant at about 3,000 between 1991 and 1999, over the same period the number of trial research contracts with nonacademic investigators increased from about 1,700 to 5,000.
Importantly, multisite clinical trials have also become increasingly global in nature, recruiting patients in many countries simultaneously. For a large Phase III trial evaluating cardiovascular or central nervous system drugs, more than 10,000 patients will typically be recruited at 100 to 200 sites in 10 or more countries worldwide.11 The size of dossiers filed by biopharmaceutical firms in support of new drug applications at the U.S. Food and Drug Administration has increased over time, reflecting increased complexity and detailed site-specific information: the mean number of pages per new drug application increased from 38,000 in 1977–1980 to 56,000 in 1985–1988 and 91,000 in 1989–1992.12
To date, very little information has been available on trends in the pricing of the R&D services that are the inputs to clinical trials. In 1985, BLS began publishing PPIs for various service sector industries, an effort that has expanded to include PPIs for aspects of health care delivery such as hospitals and physician services.13 However, these indexes do not cover business R&D that is contracted out. To date, the only published source of information on trends in pricing in the biomedical R&D sector is the Biomedical R&D Price Index, published by NIH under contract to BEA. This index is based on a chained Laspeyres methodology that uses budget microdata from individual NIH investigator grants. The Biomedical R&D Price Index measures changes in the weighted average of the prices of all the inputs (e.g., personnel services, various supplies, and equipment) that are purchased or leased with the NIH budget to support research. Input weights reflect the changing actual shares of total NIH expenditures on each of the types of inputs purchased.14 According to NIH,
Theoretically, the annual change in the [Biomedical R&D Price Index] indicates how much NIH expenditures would need to increase, without regard to efficiency gains or changes in government priorities, to compensate for the average increase in prices due to inflation and to maintain NIH-funded research activity at the previous year’s level.15
The index is published annually on a federal government fiscal-year (October 1–September 30) basis and reaches back to 1950.
In addition to contributing to the broader effort to construct measures of real R&D output, the development of a constant-quality PPI for clinical R&D would provide insights into important policy issues specific to that sector. For example, although total R&D spending by PhRMA member companies has almost doubled over the last decade 16 (as has the overall NIH budget),17 the number of new drugs and biologics approved by the U.S. Food and Drug Administration each year in the last decade has not yet returned to its mid-1990s peak levels. One prominent study reports that the capitalized cost of bringing a new drug to market, adjusted for general inflation in year-2000 dollars, more than doubled, from $318 million to $802 million, between 1991 and 2003.18
This increasing cost of bringing a new drug to market raises some very basic—and as yet unanswered—questions. Increases in the cost per approved drug are often equated with “the price of innovation,” but in fact, little is known about how much of the increase in expenditure reflects changes in the prices of inputs to biomedical research and how much reflects changes in the quantity and complexity of the research being performed. Have the prices of inputs to clinical research increased more rapidly than overall inflation, or are these inputs being used more intensively, or are both occurring? Moreover, to what extent has the “quality” of inputs changed? The growing complexity of clinical trials and of the underlying science suggests that more time, more highly trained personnel, and more sophisticated equipment may be required to conduct a typical study.19
Currently, there is a paucity of data that would inform a discussion of such issues. Although data do exist on some inputs to clinical research, such as salaries of postdoctoral fellows, relatively little is known about other important inputs to clinical research, such as site administration costs, computational time, the cost of materials, and the salaries of investigators. Critically, even where good data are available on input prices, it is important to take into account how inputs are combined. In this regard, it is crucial to focus on an appropriate unit of analysis.20
More generally, in the language of the economics of price measurement, what is needed are measures of “constant-quality” changes in prices and quantities—that is, measures that hold the characteristics of the input and output activities constant in looking at changes in expenditures over time or cross-sectionally. The failure to do so can result in quite misleading interpretations and policy recommendations. Analyses of expenditures on personal computers, for example, recognize that there have been large increases in the performance or capabilities of the products sold, but very small changes in their nominal prices. “Constant-quality” prices have thus fallen substantially over time: estimates suggest sustained real price declines of more than 25 percent per year over several decades.21 Various governmental statistical agencies now routinely take this phenomenon into account for many types of information technology and other electronic goods in developing estimates of GDP, with quite marked impacts on measures of economic growth and productivity.22
While it is important, therefore, to quantify the “price” versus “quantity” component changes in R&D and to adjust both for “quality” (in the sense of heterogeneity in characteristics of the activity), characterizing scientific research presents some substantial measurement problems. Research activities are typically highly heterogeneous and idiosyncratic in nature, drawing on quite different inputs and resources to produce an output that is difficult to measure consistently. In one respect, however, clinical trials may be unusually tractable: clinical development is a highly structured activity in which individual “experiments” are relatively well defined and activities are closely tracked. Industry trends also are creating an unusual opportunity to investigate the questions posed several paragraphs ago. Although biopharmaceutical companies and nonprofit entities continue to be the lead sponsors of clinical trials, much of the effort in conducting such trials is increasingly being outsourced to CROs rather than being expended in-house. At least within the United States, the investigators who recruit, treat, and observe subjects are being drawn less from academic medical centers and more and more from independent physician practices.23 This development has meant that data on contractual terms among all these parties are now ever more important and increasingly visible.
The sections that follow report results from a study directed at assessing the feasibility of constructing a PPI for clinical trial research from actual transactions data for contracted research services. Specifically, we analyze a sample of more than 215,000 contracts specifying payments made by trial sponsors (directly or through CRO intermediaries) to clinical investigators and study sites. The sample is from the PICAS® database maintained by Medidata Solutions, Inc. (hereafter, Medidata), and covers over 24,000 distinct Phase I through Phase IV clinical study protocols in 15 different therapeutic classes conducted between 1989 and 2011 in 52 different countries. Using information on the characteristics of the protocols, we estimate parameters in multiple regression equations and compute hedonic price indexes that allow us to estimate the rate of inflation in this particular aspect of clinical research, controlling for changes in the characteristics of clinical trials over the sample period. Because hedonic price indexes based on regression equations estimated with the use of data pooled over time would entail revising the historical price index time series each time another period of data was added to the sample, we also investigate (1) the use of chained indexes based on sequential “adjacent year” regressions; (2) the use of Paasche, Laspeyres, and Fisher Ideal indexes based on single-year regression equations; and (3) the use of Paasche, Laspeyres, and Fisher Ideal indexes under a “pure hedonic” approach in which year-on-year changes in the estimated price of characteristics are weighted by once-lagged (Laspeyres) or current-period (Paasche) quantities.24
We find that although, over the two decades covered by the sample, our measure of unit costs of this aspect of conducting clinical trials rose by about 8 percent per year (roughly twice the rate of inflation in the NIH Biomedical R&D Price Index), these changes in nominal costs appear to be driven by a variety of factors other than input costs. At least in this sample, there has been a substantial increase in the level of effort required by investigators, as well as notable changes in the composition of the sample across therapeutic classes, in the stages of clinical development, and in the organization of trials, with a trend toward smaller numbers of patients per site and considerable variation over time in the geographic distribution of foreign (hereafter, ex-U.S.) sites. After controlling for these factors by using a variety of hedonic regression methods, we find much lower growth rates in costs, with adjusted rates of inflation one-third to two-thirds less than those seen in the unadjusted data. Interestingly, we find that, for U.S. data between 1989 and 2011, growth in the price index that is based on our preferred hedonic price regression specification is virtually identical to that in the Biomedical R&D Price Index.
With the cooperation of Medidata, we assembled a dataset of 216,076 observations on investigator grants, which are contractually arranged payments made by a trial sponsor to the individual investigators, or “sites,” that enroll subjects.25 The payments cover the investigators’ costs of recruiting subjects, administering treatments, measuring clinical endpoints, etc., plus overhead allowances reflecting payments for the use of the site’s facilities. We focus on the total grant cost per patient as the economically meaningful unit of analysis for understanding price trends. The total grant cost per patient is the total amount paid by the sponsor under its contract with the site, divided by the number of patients planned to be enrolled at that site. For about 12 percent of the records contained in the PICAS database, the contract specifies only a per-patient amount, not the anticipated number of patients, and these contracts are excluded from the analysis, because we are unable to control for the scale of the site’s effort. For ex-U.S. sites where the contract is in a foreign currency, we convert to U.S. dollars by using the spot exchange rate prevailing on the date the contract was signed. Typically, these payments make up about half of the total cost of a trial, the remainder being headquarters’ overhead in the form of trial design, data management and analysis, site selection and monitoring, etc., by the sponsors.
Table 1 gives a summary of the number of records in the dataset by the year each investigator contract was signed, along with summary statistics for the total grant cost per patient. The dataset used covers the period from 1989 to 2011, almost a quarter of a century. The number of records per year varies over time, with the period 1992–2002 accounting for almost 75 percent of the total number of records. The number of records per year reached a peak in 2000 and declined steadily thereafter, reflecting two factors. First, the PICAS database was originally compiled from an archive of paper records and has since transitioned to electronic source documents. The transition led to a temporary decline in the number of contributions from the participating organizations in 2004–2005. Second, the fraction of contracts that do not specify the number of patients expected to be enrolled at the site (and hence that are excluded from the sample) has increased over the past decade. This trend likely reflects sponsors’ tighter “real-time” tracking and control of patient enrollment, as well as challenges in sites being equally able to enroll their planned number of patients in a timely manner.
| Year | Mean | Median | Standard deviation | N |
|---|---|---|---|---|
| All years (1) | $6,191.80 | $4,195.07 | $6,860.91 | 216,076 |
| 1989 | 3,772.59 | 2,779.43 | 2,921.34 | 1,370 |
| 1990 | 4,385.77 | 3,147.77 | 4,016.57 | 3,443 |
| 1991 | 3,774.43 | 2,774.83 | 4,186.06 | 92,88 |
| 1992 | 3,493.63 | 2,399.00 | 6,129.31 | 14,126 |
| 1993 | 3,664.58 | 2,325.45 | 4,254.28 | 15,733 |
| 1994 | 3,911.39 | 2,882.35 | 3,925.46 | 16,625 |
| 1995 | 4,183.00 | 3,203.85 | 3,941.90 | 15,670 |
| 1996 | 4,884.89 | 3,748.77 | 4,708.14 | 14,442 |
| 1997 | 4,549.12 | 3,200.00 | 4,422.39 | 13,321 |
| 1998 | 5,393.70 | 3,948.38 | 5,445.89 | 14,370 |
| 1999 | 5,501.08 | 4,361.94 | 4,874.07 | 13,943 |
| 2000 | 6,220.42 | 4,682.79 | 6,243.02 | 18,671 |
| 2001 | 6,078.96 | 4,777.00 | 5,150.11 | 16,864 |
| 2002 | 6,567.58 | 4,744.10 | 5,984.32 | 12,201 |
| 2003 | 8,147.90 | 6,765.00 | 6,866.55 | 6,515 |
| 2004 | 10,264.00 | 8,582.72 | 7,758.22 | 3,216 |
| 2005 | 11,412.77 | 9,682.02 | 7,828.89 | 2,693 |
| 2006 | 12,364.68 | 10,900.00 | 7,460.17 | 4,012 |
| 2007 | 13,001.19 | 10,738.47 | 8,863.90 | 4,764 |
| 2008 | 14,834.64 | 12,720.94 | 10,328.42 | 3,216 |
| 2009 | 16,518.28 | 13,965.42 | 12,550.80 | 4,591 |
| 2010 | 15,099.19 | 12,581.93 | 10,860.27 | 4,814 |
| 2011 | 16,566.55 | 13,222.14 | 13,556.92 | 2,188 |
| Notes: (1) Computed from the pooled 1989–2011 sample. Note: Based on 216,076 observations for which total grant cost and PATIENTS were not missing. Total grant cost is measured in nominal U.S. dollars for each site. PATIENTS is the number of patients anticipated to be enrolled at each site. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | ||||
As can be seen from the table, over the period from 1989 to 2011 the mean total grant cost per patient rose quite rapidly in nominal terms, slightly more than fourfold, from $3,773 to $16,567, with an average annual growth rate of 7.5 percent;26 the median value for each year increased slightly more rapidly, from $2,779 to $13,222, an average annual growth rate of 8.2 percent.27 By contrast, between fiscal years 1989 and 2011 the Biomedical R&D Price Index increased much more slowly, barely doubling, with an average annual growth rate only half as large, at 3.7 percent.28 The distribution of total grant cost per patient is quite skewed, with the median somewhat below the mean value; a visual plot suggests that this variable can be reasonably approximated with a lognormal distribution. Notably, the within-year coefficient of variation is relatively large but stable, at around 0.80, at both the beginning and end of the sample period. Although we attempt to account for this variation in total grant cost per patient with measured site and protocol characteristics, some part is likely attributable to factors such as the conversion of foreign transactions to U.S. dollars, using the spot exchange rate at the time of the transaction.
| Year | Mean site work effort | Median site work effort |
|---|---|---|
1989 | 16.96 | 13.10 |
1990 | 16.58 | 13.56 |
1991 | 15.23 | 11.27 |
1992 | 17.55 | 13.24 |
1993 | 18.96 | 13.70 |
1994 | 21.64 | 16.40 |
1995 | 23.53 | 18.11 |
1996 | 23.49 | 18.71 |
1997 | 24.82 | 19.11 |
1998 | 26.02 | 19.69 |
1999 | 27.28 | 20.62 |
2000 | 27.99 | 22.26 |
2001 | 29.56 | 22.78 |
2002 | 29.12 | 21.89 |
2003 | 35.92 | 29.94 |
2004 | 43.28 | 34.23 |
2005 | 47.28 | 39.06 |
2006 | 46.51 | 36.92 |
2007 | 38.01 | 31.20 |
2008 | 48.91 | 42.47 |
2009 | 48.43 | 40.35 |
2010 | 46.20 | 38.89 |
2011 | 47.51 | 41.10 |
Notes: Source: Author's calculations based on Medidata Solutions, Inc.'s, PICAS® database. | ||
| Year | Mean number of patients per site | Median number of patients per site |
|---|---|---|
1989 | 25.48 | 20 |
1990 | 21.26 | 15 |
1991 | 20.64 | 15 |
1992 | 18.50 | 12 |
1993 | 17.04 | 12 |
1994 | 16.37 | 12 |
1995 | 14.39 | 10 |
1996 | 14.83 | 10 |
1997 | 14.14 | 10 |
1998 | 14.60 | 10 |
1999 | 13.85 | 10 |
2000 | 11.27 | 9 |
2001 | 12.11 | 10 |
2002 | 12.07 | 10 |
2003 | 13.30 | 10 |
2004 | 12.18 | 9 |
2005 | 10.73 | 10 |
2006 | 11.80 | 10 |
2007 | 10.30 | 9 |
2008 | 11.10 | 7 |
2009 | 11.81 | 8 |
2010 | 11.79 | 8 |
2011 | 11.83 | 8 |
Source: Author's calculations based on Medidata Solutions, Inc.'s, PICAS® database. | ||
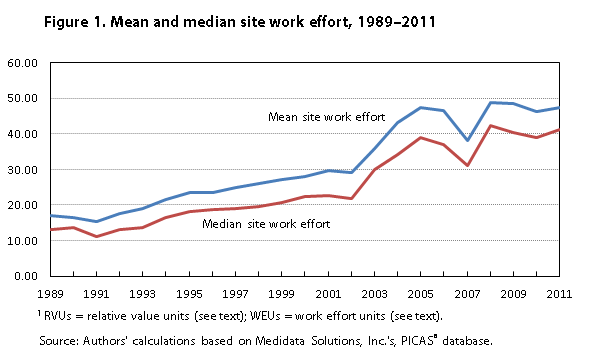
Table 2 and figures 1 and 2 show two important aspects of trials that affect the costs incurred by an investigator: site work effort and number of patients. Site work effort is a patent-pending measure of clinical trial complexity and burden. Developed by Medidata, the measure was constructed as follows: On the basis of an examination of detailed study protocols, the number and intensity of use of various procedures and the use of certain diagnostic technologies were assigned to each procedure in a trial protocol. Among the procedures assigned were laboratory tests, bloodwork, questionnaires and subjective assessments, and office consultations and examinations; among the diagnostic technologies assigned were x rays, imaging or heart activity assessments, relative value units (RVUs),29 or, where the latter were unavailable or inapplicable, comparable work effort units (WEUs) created by Medidata in conjunction with researchers at the Tufts Center for Study of Drug Development. A complexity measure was computed simply as the number of distinct procedures in the trial protocol. An aggregate investigative site work effort measure was then computed as the cumulated product of the number and intensity in use of these procedures, in RVU/WEU units, conducted over the course of the entire protocol for each of the trials.30 It is important to note that site work effort is therefore a trial-level measure of the work effort required to implement the study protocol and that the actual resources used by each site in implementing the protocol may differ to some degree.31 Figure 1 and panel (a) of table 2 report descriptive statistics for site work effort for the 24,172 distinct protocols in the sample for which such effort was observed. As these data show, the mean and median values of site work effort increased substantially over time, with the mean value per protocol rising almost threefold between 1989 and 2011, at average annual growth rates of 5.2 percent (mean) and 6.1 percent (median).32
| Year | (a) Site work effort (SWE) (trial level) | (b) Patients (site level) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Median | Standard deviation | N | Mean | Median | Standard deviation | N | |
| All years (1) | 25.93 | 19.20 | 23.28 | 24,172 | 14.42 | 10 | 22.58 | 216,076 |
| 1989 | 16.96 | 13.10 | 13.05 | 242 | 25.48 | 20 | 33.25 | 1,370 |
| 1990 | 16.58 | 13.56 | 12.96 | 500 | 21.26 | 15 | 27.32 | 3,443 |
| 1991 | 15.23 | 11.27 | 12.58 | 1,287 | 20.64 | 15 | 32.42 | 9,288 |
| 1992 | 17.55 | 13.24 | 15.24 | 1,845 | 18.50 | 12 | 25.25 | 14,126 |
| 1993 | 18.96 | 13.70 | 17.83 | 2,027 | 17.04 | 12 | 24.58 | 15,733 |
| 1994 | 21.64 | 16.40 | 18.17 | 1,950 | 16.37 | 12 | 24.63 | 16,625 |
| 1995 | 23.53 | 18.11 | 21.49 | 1,822 | 14.38 | 10 | 26.52 | 15,670 |
| 1996 | 23.49 | 18.71 | 18.66 | 1,790 | 14.83 | 10 | 36.30 | 14,442 |
| 1997 | 24.82 | 19.11 | 20.28 | 1,539 | 14.14 | 10 | 17.68 | 13,321 |
| 1998 | 26.02 | 19.69 | 20.14 | 1,496 | 14.60 | 10 | 25.00 | 14,370 |
| 1999 | 27.28 | 20.62 | 24.88 | 1,391 | 13.85 | 10 | 17.02 | 13,943 |
| 2000 | 27.99 | 22.26 | 22.28 | 1,891 | 11.26 | 9 | 14.71 | 18,671 |
| 2001 | 29.56 | 22.78 | 23.21 | 1,883 | 12.10 | 10 | 13.86 | 16,864 |
| 2002 | 29.12 | 21.89 | 24.48 | 1,393 | 12.06 | 10 | 12.15 | 12,201 |
| 2003 | 35.92 | 29.94 | 27.47 | 909 | 13.09 | 10 | 18.26 | 6,515 |
| 2004 | 43.28 | 34.23 | 34.27 | 563 | 11.89 | 9 | 12.48 | 3,216 |
| 2005 | 47.28 | 39.06 | 37.79 | 307 | 10.78 | 10 | 14.10 | 2,693 |
| 2006 | 46.51 | 36.92 | 36.11 | 265 | 11.78 | 10 | 9.57 | 4,012 |
| 2007 | 38.01 | 31.20 | 23.24 | 230 | 10.30 | 9 | 8.48 | 4,764 |
| 2008 | 48.91 | 42.47 | 35.52 | 174 | 11.16 | 6 | 20.17 | 3,216 |
| 2009 | 48.43 | 40.35 | 34.92 | 272 | 11.96 | 8 | 15.66 | 4,591 |
| 2010 | 46.20 | 38.89 | 31.30 | 271 | 11.89 | 8 | 23.87 | 4,814 |
| 2011 | 47.51 | 41.10 | 34.97 | 125 | 11.83 | 8 | 17.11 | 2,188 |
| Notes: (1) Computed from the pooled 1989–2011 sample.Note: Panel (a) is based on 24,172 distinct trials (clinical studies) for which TGPP and SWE were not missing. Panel (b) is based on the 216,076 investigator contracts within these trials for which TGPP and PATIENTS were not missing and includes 8,126 for which SWE was not coded. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | ||||||||
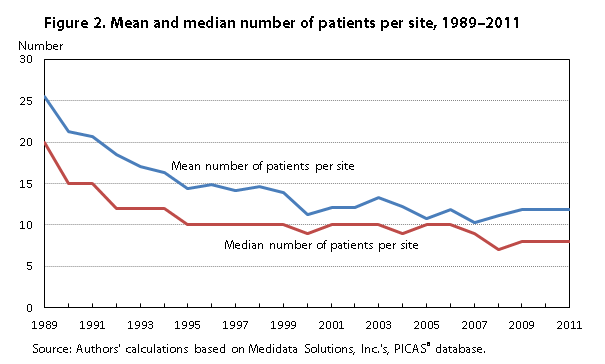
By contrast, as seen in panel (b) of table 2 and in figure 2, the mean number of patients per site fell considerably over the same period, from 25.48 to 11.83, a diminution by a factor of about 2, and the median fell even more dramatically, from 20 to 8. The relative volatility (coefficient of variation) of the number of patients per site increased steadily, from about 1.3 in 1989 to about 1.7 in 1999–2000 and to 2.0 in 2010, while that for site work effort was relatively stable, at about 0.7.
| Year | Phase I | Phase II | Phase IIa | Phase IIIb | Phase IV |
|---|---|---|---|---|---|
| All years (1) | 3.67 | 19.25 | 53.03 | 11.19 | 12.85 |
| 1989 | 2.12 | 9.12 | 72.55 | 6.35 | 9.85 |
| 1990 | 3.08 | 13.94 | 69.53 | 5.84 | 7.61 |
| 1991 | 3.45 | 15.13 | 50.67 | 12.75 | 18.01 |
| 1992 | 3.58 | 14.14 | 58.47 | 6.98 | 16.82 |
| 1993 | 3.96 | 18.34 | 56.79 | 4.74 | 16.16 |
| 1994 | 3.70 | 18.80 | 58.69 | 7.65 | 11.16 |
| 1995 | 4.20 | 20.53 | 54.22 | 6.64 | 14.42 |
| 1996 | 4.84 | 23.09 | 52.94 | 8.55 | 10.58 |
| 1997 | 4.14 | 18.08 | 56.53 | 8.85 | 12.40 |
| 1998 | 3.63 | 19.08 | 49.45 | 13.84 | 13.99 |
| 1999 | 4.05 | 20.35 | 49.26 | 14.08 | 12.26 |
| 2000 | 3.38 | 17.52 | 49.91 | 17.74 | 11.43 |
| 2001 | 3.65 | 16.59 | 50.15 | 14.98 | 14.63 |
| 2002 | 2.98 | 21.02 | 46.87 | 16.56 | 12.56 |
| 2003 | 4.11 | 17.93 | 44.94 | 16.64 | 16.38 |
| 2004 | 4.66 | 23.48 | 42.01 | 18.10 | 11.75 |
| 2005 | 2.41 | 25.66 | 51.06 | 9.32 | 11.55 |
| 2006 | 3.24 | 15.33 | 69.42 | 3.34 | 8.67 |
| 2007 | 2.18 | 25.90 | 49.75 | 15.55 | 6.61 |
| 2008 | 3.05 | 23.38 | 47.42 | 16.76 | 9.39 |
| 2009 | 3.55 | 23.74 | 57.87 | 7.91 | 6.93 |
| 2010 | 2.47 | 31.91 | 45.74 | 12.21 | 7.67 |
| 2011 | 1.60 | 25.82 | 55.44 | 6.76 | 10.37 |
| Notes: (1) Computed from the pooled 1989–2011 sample. Note: Table entries are the fraction of investigator contracts in the year shown for trials at the indicated phase of clinical development. Based on 216,076 total observations of investigator contracts for which TGPP and PATIENTS were not missing. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | |||||
These changes in nominal total grant cost per patient, site work effort, and number of patients per site suggest that important changes are occurring in the cost and nature of outsourced clinical research. Of course, some of the trends may reflect a changing composition of the sample in the mix of therapeutic areas and phases of research and in the location of sites in the United States versus those in other countries. Tables 3 through 5 provide descriptive statistics on the composition of the sample by various trial characteristics. Table 3 breaks out the fraction of observations annually by the stage of development of the study protocol. Clinical trials are conventionally categorized by stage of development. Phase I trials typically enroll a small number of healthy volunteers and are focused on safety, tolerability, pharmacokinetics, range of dose, and more. Phase II trials enroll larger numbers of patients (not healthy volunteers) and investigate the potential for efficacy by assessing biological activity or effect of the treatment at alternative putatively safe doses. Phase III trials focus on efficacy of the treatment in therapeutic use, enrolling large numbers of patients. Phase IIIa trials are those conducted before making a submission for regulatory approval, while Phase IIIb trials are those initiated after the submission for approval but prior to commercial launch of the product. Phase IV trials are conducted after a drug has been approved; often, the trials are part of a continuing investigation of safety. Although the fraction of the sample made up by sites involved in Phase I, Phase IIIb, and Phase IV studies was approximately stable, there has been a significant swing in the shares of Phase II and Phase IIIa. In 1989, Phase II trials made up less than 10 percent of the sample, Phase IIIa trials almost 75 percent. By the end of the sample period in 2011, Phase II studies accounted for almost 30 percent of trials and Phase IIIa studies dropped to under 60 percent. If early-stage trials are more costly to conduct on a per-patient basis, then this shift among trial phases may account for some of the increase in mean total grant cost per patient over time.
Table 4 presents the allocation of investigator grants over 15 different therapeutic areas. Reflecting the burden of disease, trials involving the six therapeutic areas most commonly studied in our sample (central nervous system, cardiovascular, respiratory system, endocrine, oncology, and anti-infectives) make up 70 percent of the sample, on average. Although the increases were neither uniform nor steady, in general, shares of central nervous system and oncology trials grew somewhat over time until 2005–2006, while shares of cardiovascular trials shrank, suggesting that, to the extent that central nervous system and oncology trials are relatively more costly to conduct, these compositional changes may have some effect on increases in average total grant cost per patient up to 2005–2006.
| Year | Anti-Infective | Cardiovascular | Central nervous system | Dermatology | Devices and diagnostics | Endocrine | Gastrointestinal |
|---|---|---|---|---|---|---|---|
| All years (1) | 7.89 | 14.76 | 16.20 | 2.56 | 0.47 | 11.44 | 5.31 |
| 1989 | 7.66 | 14.82 | 14.38 | 4.09 | .00 | 3.28 | 10.07 |
| 1990 | 9.09 | 21.64 | 9.70 | 2.27 | .20 | 7.29 | 9.00 |
| 1991 | 8.81 | 18.62 | 14.69 | 2.45 | .12 | 6.01 | 13.18 |
| 1992 | 8.10 | 16.69 | 15.33 | 2.63 | .27 | 5.88 | 9.80 |
| 1993 | 10.13 | 19.70 | 14.37 | 2.58 | .35 | 7.29 | 9.92 |
| 1994 | 11.56 | 20.82 | 16.72 | 2.15 | .48 | 6.42 | 6.35 |
| 1995 | 8.07 | 18.66 | 16.66 | 2.07 | .05 | 6.46 | 4.43 |
| 1996 | 8.42 | 16.45 | 17.50 | 1.88 | .18 | 7.57 | 3.82 |
| 1997 | 6.58 | 15.54 | 19.06 | 1.73 | .29 | 9.10 | 4.51 |
| 1998 | 7.24 | 15.85 | 15.49 | 2.75 | .15 | 11.69 | 1.88 |
| 1999 | 5.49 | 18.89 | 14.08 | 2.36 | .32 | 11.93 | 2.76 |
| 2000 | 6.94 | 15.30 | 14.85 | 2.40 | .52 | 13.63 | 3.37 |
| 2001 | 10.58 | 9.36 | 13.94 | 2.83 | .15 | 14.85 | 5.22 |
| 2002 | 6.41 | 8.42 | 13.83 | 2.03 | .17 | 17.32 | 3.85 |
| 2003 | 8.73 | 9.41 | 23.22 | 6.17 | .87 | 12.28 | 2.09 |
| 2004 | 5.78 | 10.91 | 28.64 | 1.90 | 1.09 | 13.09 | .40 |
| 2005 | 4.90 | 20.61 | 21.83 | 3.97 | 1.15 | 4.23 | 2.15 |
| 2006 | 2.32 | 12.09 | 27.14 | 2.47 | .15 | 19.52 | 3.32 |
| 2007 | 4.79 | 4.45 | 17.59 | 1.18 | .31 | 18.49 | 7.49 |
| 2008 | 3.86 | 6.13 | 16.48 | 3.89 | .65 | 21.77 | 5.75 |
| 2009 | 9.74 | 1.66 | 17.86 | 1.81 | 2.31 | 24.29 | 5.10 |
| 2010 | 6.77 | .98 | 12.34 | 5.11 | 2.74 | 32.05 | 4.26 |
| 2011 | 1.37 | .46 | 14.76 | 6.17 | 6.08 | 28.93 | .05 |
| Notes: (1) Computed from the pooled 1989–2011 sample. Note: Table entries are the fraction of investigator contracts in the year shown for studies in the indicated therapeutic area. Based on 216,076 total observations for which TGPP and PATIENTS were not missing. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | |||||||
| Year | Genitourinary System | Hematology | Immuno-modulation | Oncology | Ophthalmology | Pain and Anesthesia | Pharmaco-kinetics | Respiratory System |
|---|---|---|---|---|---|---|---|---|
| All years (1) | 6.98 | 1.62 | 7.45 | 8.99 | 1.39 | 2.36 | 1.99 | 10.60 |
| 1989 | 10.51 | 0.58 | 18.76 | 5.84 | 1.68 | 1.61 | 1.68 | 5.04 |
| 1990 | 5.14 | 1.95 | 7.75 | 8.51 | 8.19 | .46 | 1.54 | 7.26 |
| 1991 | 5.33 | .39 | 8.57 | 4.94 | 2.57 | 1.07 | 2.02 | 11.24 |
| 1992 | 8.58 | .42 | 6.26 | 5.12 | .68 | 3.27 | 2.10 | 14.87 |
| 1993 | 9.76 | .70 | 6.06 | 3.37 | .66 | .90 | 2.07 | 12.15 |
| 1994 | 5.73 | .94 | 6.09 | 4.84 | 1.41 | .87 | 2.36 | 13.27 |
| 1995 | 7.45 | .54 | 5.34 | 8.22 | 1.07 | 1.33 | 2.29 | 17.35 |
| 1996 | 4.94 | 1.70 | 7.55 | 9.60 | .80 | 2.85 | 2.51 | 14.21 |
| 1997 | 6.51 | .62 | 5.33 | 10.81 | 1.70 | 1.37 | 2.67 | 14.17 |
| 1998 | 8.20 | 1.75 | 5.82 | 10.51 | 1.34 | 1.51 | 2.39 | 13.43 |
| 1999 | 6.66 | 3.13 | 10.23 | 10.44 | 1.78 | 2.20 | 2.57 | 7.16 |
| 2000 | 5.58 | 3.29 | 7.06 | 11.20 | .59 | 2.13 | 1.86 | 11.28 |
| 2001 | 7.60 | 1.41 | 9.28 | 10.45 | 1.20 | 2.99 | 1.87 | 8.25 |
| 2002 | 9.86 | 1.89 | 9.65 | 10.22 | 1.52 | 4.60 | 1.54 | 8.68 |
| 2003 | 4.87 | 2.10 | 6.54 | 10.64 | 1.30 | 4.24 | 1.92 | 5.62 |
| 2004 | 8.05 | 4.01 | 9.89 | 10.26 | .56 | .28 | 2.30 | 2.83 |
| 2005 | 2.34 | 6.24 | 7.91 | 18.86 | .37 | 1.56 | 1.04 | 2.82 |
| 2006 | 3.39 | .30 | 8.03 | 11.17 | 1.02 | 6.51 | .60 | 1.99 |
| 2007 | 11.52 | .65 | 9.53 | 8.42 | .76 | 7.37 | .11 | 7.35 |
| 2008 | 5.26 | .59 | 15.52 | 15.14 | 1.96 | 2.27 | .22 | .53 |
| 2009 | 7.78 | 1.63 | 7.93 | 14.22 | 1.50 | 2.03 | .63 | 1.52 |
| 2010 | 5.42 | 1.89 | 5.23 | 11.67 | 2.68 | 6.19 | .77 | 1.89 |
| 2011 | 3.06 | 10.10 | 5.44 | 12.34 | 6.12 | 1.10 | 2.47 | 1.55 |
| Notes: (1) Computed from the pooled 1989–2011 sample. Note: Table entries are the fraction of investigator contracts in the year shown for studies in the indicated therapeutic area. Based on 216,076 total observations for which TGPP and PATIENTS were not missing. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | ||||||||
Table 5 presents the geographic breakdown of the sites in the sample. Over the entire sample period, 56 percent of sites were in the United States, with most of the remainder in other member countries of the Organisation for Economic Co-operation and Development (OECD) and only 5.4 percent in the rest of the world. Note that, although the U.S. share is about 80 percent in both the earliest and latest years, there is substantial year-to-year and trend variability. However, as shown in Table 1, there are considerably smaller numbers of observations in 1989–1991 and 2003–2011 relative to the 1992–2002 period; any trend analysis is therefore tentative.
| Year | (a) U.S. sites vs. Ex-U.S. sites | (b) Ex-U.S. sites | ||
|---|---|---|---|---|
| U.S. sites | Sites in rest of world | OECD member sites | Other sites | |
| All years (1) | 55.87 | 44.13 | 94.61 | 5.39 |
| 1989 | 81.82 | 18.18 | 100.00 | .00 |
| 1990 | 77.17 | 22.83 | 99.11 | .89 |
| 1991 | 67.51 | 32.49 | 99.83 | .17 |
| 1992 | 49.19 | 50.81 | 99.79 | .21 |
| 1993 | 47.31 | 52.69 | 99.59 | .41 |
| 1994 | 46.57 | 53.43 | 99.64 | .36 |
| 1995 | 47.51 | 52.49 | 99.60 | .40 |
| 1996 | 55.24 | 44.76 | 99.75 | .25 |
| 1997 | 48.18 | 51.82 | 98.87 | 1.13 |
| 1998 | 46.09 | 53.91 | 98.06 | 1.94 |
| 1999 | 53.49 | 46.51 | 96.64 | 3.36 |
| 2000 | 56.40 | 43.60 | 92.21 | 7.79 |
| 2001 | 56.69 | 43.31 | 89.42 | 10.58 |
| 2002 | 54.30 | 45.70 | 90.62 | 9.38 |
| 2003 | 53.61 | 46.39 | 92.26 | 7.74 |
| 2004 | 56.93 | 43.07 | 91.99 | 8.01 |
| 2005 | 64.87 | 35.13 | 88.79 | 11.21 |
| 2006 | 85.42 | 14.58 | 85.30 | 14.70 |
| 2007 | 87.91 | 12.09 | 60.59 | 39.41 |
| 2008 | 70.43 | 29.57 | 59.52 | 40.48 |
| 2009 | 79.98 | 20.02 | 70.73 | 29.27 |
| 2010 | 78.04 | 21.96 | 74.17 | 25.83 |
| 2011 | 69.15 | 30.85 | 56.00 | 44.00 |
| Notes: (1) Computed from the pooled 1989–2011 sample. Note: Panel (a) is based on 24,172 distinct trials (clinical studies) for which TGPP and SWE were not missing. Panel (b) is based on the 216,076 investigator contracts within these trials for which TGPP and PATIENTS were not missing and includes 8,126 for which SWE was not coded. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | ||||
The hedonic pricing approach has a long tradition in economic measurement, going back almost a century.33 In essence, the approach treats the item being priced as a bundle of observed characteristics and uses multivariate regression methods to estimate “shadow prices” of each of those characteristics and to estimate the aggregate price index as a composite of the characteristics, each multiplied by its shadow price. In practice, given observations of the prices Pit of a set of items i with characteristics Xit in each period t, the hedonic approach estimates a regression model on pooled data of the form ln(Pit) = Xitß + Ztγ + εit, where Zt is a set of dummy variables for each period, εit is a random-error term, and the other variables and parameters are as defined in the next paragraph. This semilogarithmic functional form is widely used in hedonic price analysis.34 Predicted values from the regression provide the basis for computing changes in a “quality-adjusted” composite price index Pt: with a set of time dummies in the regression, the change in the composite index relative to the base period is given by exponentiation of the values of their estimated coefficients (![]() ). Although E[exp(P)] ≠ exp(E[P]) and εit may not be homoskedastic, suggesting a “smearing” adjustment of the type discussed in the medical costs literature,35 with time dummies in the regression these adjustment factors will typically be small.36 (In the case where residuals are homoskedastic within periods but heteroskedastic across time, adjusted values such as those produced by the nonparametric method proposed by Duan will give estimates that are numerically identical to unadjusted values produced by other methods.37 We found similar adjusted and unadjusted estimated index values, so in this article we report only estimates with no further adjustment for cross-year heteroskedasticity.)
). Although E[exp(P)] ≠ exp(E[P]) and εit may not be homoskedastic, suggesting a “smearing” adjustment of the type discussed in the medical costs literature,35 with time dummies in the regression these adjustment factors will typically be small.36 (In the case where residuals are homoskedastic within periods but heteroskedastic across time, adjusted values such as those produced by the nonparametric method proposed by Duan will give estimates that are numerically identical to unadjusted values produced by other methods.37 We found similar adjusted and unadjusted estimated index values, so in this article we report only estimates with no further adjustment for cross-year heteroskedasticity.)
In this application of hedonic pricing, the item being priced is the investigator total grant cost per patient and our hedonic regression takes the form ln(TGPPit) = Xitß + Ztγ + εit, where TGPPit is the total grant cost per patient for item i during period t; Xit denotes site and trial characteristics, including the planned number of patients at the investigator’s site, the location and number of sites and countries participating in the trial, the phase of development, the therapeutic area, and the site work effort measure of trial burden and complexity; Zt are annual indicator variables; and ß, γ, and εit are as before. We treat the planned number of patients at the investigator’s site as an exogenous, or predetermined, variable. Because the dependent variable is the logarithm of investigator TGPP, which incorporates the logarithm of the number of patients in its calculation, and because the logarithm of PATIENTS is included as a regressor in order to investigate whether there are scale economies in the specification of our multivariate regression, LPATIENTS appears on both the left- and right-hand side of the equation. In this case, the absence of any scale economies, the presence of positive scale economies, and the presence of negative scale economies correspond, respectively, to a zero, negative, and positive estimated coefficient of the LPATIENTS regressor.38 Estimated standard errors are Huber–White robust, clustered by trial protocol; computations were carried out in STATA.
In this section, we report results based on various regressions and calculate corresponding average annual growth rates of implied hedonic price indexes. Although all regressions have as regressors indicator variables for therapeutic class and year, we pool over and then run separate regressions by trial phase; we also pool over the entire 1989–2011 period and then run separate regressions for the 1989–1999 and 2000–2011 subperiods.39 In all cases, the dependent variable is the logarithm of total grant cost per patient, ln(TGPP).40
Of particular interest are the coefficient estimates for two clinical trial characteristics variables: the site work effort (hereafter, SWE, for purposes of the regression)41 and the logarithm of the number of patients at the site (LPATIENTS). Note that we have no expectation regarding the sign of the coefficient of LPATIENTS; a negative estimate implies economies of scale at the site level, a positive estimate diseconomies of scale. By contrast, because SWE measures the cumulative burden of various clinical trial protocol procedures, we expect it to have a positive coefficient. Parameter estimates for these two variables under alternative models and periods are presented in table 6. With two exceptions (both involving LPATIENTS in Phase II trials), all of the estimated coefficients are statistically significant at the 1-percent level, based on robust standard errors.
| Parameter and phase | Pooled 1989–2011 | 1989–1999 | 2000–2011 | |||
|---|---|---|---|---|---|---|
| LPATIENTS | SWE | LPATIENTS | SWE | LPATIENTS | SWE | |
| Phases pooled: | ||||||
| All | 0.148 | 0.021 | 0.183 | 0.028 | 0.042 | 0.015 |
| U.S. only | –.122 | .017 | –.120 | .022 | –.117 | .014 |
| Rest of world | .124 | .023 | .128 | .030 | .054 | .016 |
| By phase: | ||||||
| All | ||||||
| Phase I | –.145 | .013 | –.168 | .016 | –.097 | .010 |
| Phase II | –.017 | .018 | –.011 (1) | .022 | –.032 | .015 |
| Phase IIIa | .120 | .020 | .173 | .029 | –.024 | .014 |
| Phase IIIb | .155 | .028 | .226 | .034 | .030 | .024 |
| Phase IV | .320 | .034 | .305 | .049 | .272 | .025 |
| By phase: | ||||||
| U.S. only | ||||||
| Phase I | –.176 | .014 | –.219 | .019 | –.104 | .010 |
| Phase II | –.164 | .016 | –.197 | .017 | –.125 | .014 |
| Phase IIIa | –.102 | .016 | –.099 | .024 | –.094 | .013 |
| Phase IIIb | –.063 | .026 | –.054 | .024 | –.051 | .026 |
| Phase IV | –.170 | .025 | –.153 | .027 | –.190 | .022 |
| By phase: | ||||||
| Rest of world | ||||||
| Phase I | –.120 | .011 | –.131 | .013 | –.080 | .008 |
| Phase II | –.010 | .019 | –.031 | .026 | –.008 (1) | .014 |
| Phase IIIa | .826 | .022 | .121 | .028 | –.059 | .016 |
| Phase IIIb | .101 | .028 | .115 | .037 | .041 | .021 |
| Phase IV | .217 | .048 | .171 | .062 | .225 | .032 |
| Note: Table entries are the estimated coefficients of LPATIENTS and SWE in a regression of ln(TGPP) on these and other explanatory variables. With the exception of the coefficients marked (1), all coefficients in the table were statistically distinguishable from zero at the p < .01 level using robust standard errors clustered by trial protocol. The phases-pooled regression includes a constant and indicator variables for therapeutic class, trial phase, and year. The by-phase regressions include a constant and indicator variables for therapeutic class and year. Based on 207,950 records with total grant cost per patient, PATIENTS, and SWE not missing. The number of observations was 207,950 in the “All” regressions, 118,477 in the “U.S. only” regressions, and 89,473 in the” Rest of world” regressions. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | ||||||
A number of results are striking. As shown in the top panel of table 6, when pooled over all phases (but including the trial phase as an indicator variable), globally and outside of the United States (the rest of the world, including OECD member countries), the estimated coefficient of LPATIENTS is positive and highly significant in all three period regressions; however, for the U.S.-only model, the coefficient estimate is negative and significant. The implied estimated elasticities of TGPP with respect to patients range from –0.122 to 0.183.
The pattern of estimates of LPATIENTS becomes a bit more nuanced when separate regressions are run by trial phase. A general pattern that prevails is that negative estimates occur for the Phase I and Phase II regressions for both all countries and the rest of the world excluding the United States, but these estimates become positive and ever larger as one moves to the increasingly larger patient-size trials. In Phase IIIa, Phase IIIb, and Phase IV trials, almost all the estimates are positive and significant, even at p < 0.01. Also notable is the substantial range in estimates of the elasticity of TGPP with respect to patients, from –0.176 to 0.320 in the pooled 1989–2011 regressions; even larger, from –0.219 to 0.305 in the 1989–1999 regressions; and from –0.190 to 0.272 in the 2000–2011 regressions. The pooled phases and the regressions by phase based on U.S.-only data reveal considerably greater stability, both across the various period regressions and across trial phases.
A second set of striking findings shown in table 6 is that every one of the estimates of the SWE variable is positive and statistically significant at p < .01, with the general (but not quite universal) pattern being that the positive estimates increase monotonically as one moves from the small Phase I to the larger Phase IIIb and Phase IV trials.42 The steepness of the positive slope with larger trial phase is flatter for the U.S.-only regressions, however, than for the regressions for all nations and for the rest of the world, with estimates for the latter two variables and for Phase IV being particularly large; the vast majority of estimates of the SWE variable are in the range from 0.01 to 0.03. Using a mean value of about 25 for SWE (see table 2), we find that a one-unit increase in this variable changes it by about 4 percent (1/25), leading to about a 2-percent increase, on average, in TGPP, suggesting an elasticity of about 0.50 (= 0.02/0.04) for TGPP with respect to SWE when evaluated at the sample means. That is a substantial effect.
A third implication of the findings listed in table 6 is that they help explain factors affecting increases in trial costs, particularly as regards the United States. The regression results suggest that increases in TGPP over time have been driven by increases in SWE and decreases in the number of patients at each site (particularly in the United States, where, for each phase coefficient, estimates of LPATIENTS are mostly negative). The extent to which these changes in SWE and patients per site observed in the data are driven by the changing composition of the sample among trial phases (toward Phase II and away from Phase IIIa—see table 3), as opposed to trends in these trial characteristics within phases, merits further examination.
We now move on to consider implications of the various regression models for the growth rate of our putative price indexes. As discussed earlier, annual values of a hedonic price index can be constructed from estimated coefficients of indicator variables by year. We summarize the growth rate of this index by computing the annual average growth rate, which is the mean of year-on-year percent changes in the index values.43 The top panel of table 7 reports estimates of annual average growth rates in a “base” hedonic model that excludes our two prominent “quality” measures, namely, LPATIENTS and SWE, which, from table 6, we have observed as being highly statistically significant. To quantify the importance of including these trial site “quality” characteristics in our hedonic regression equation, we compare annual average growth rates of predicted ln(TGPP) with and without the LPATIENTS and SWE variables by examining the relative growth of coefficients of the yearly indicator variables. The results are striking. With the pooled 1989–2011 regression (first column of table 7), TGPP grows much more slowly relative to the base model when the trial site characteristics are included: 4.31 percent versus 6.96 percent for the regressions for all nations (a 38-percent lower annual average growth rate), 3.62 percent versus 7.01 percent for the U.S.-only regressions (a 48-percent lower annual average growth rate), and 6.05 percent versus 8.70 percent for the regressions for the rest of the world (a 30-percent lower annual average growth rate). For the 1989–1999 regressions (next-to-last column of the table), the corresponding percent reductions in annual average growth rates are more modest: 6 percent for the regressions for all nations, 31 percent for the U.S.-only regressions, and 19 percent for the regressions for the rest of the world. By contrast, for the most recent (2000–2011) regressions (last column), the annual average growth rates are not only large proportionately—a 40-percent lower annual average growth rate for the regressions for all nations, 56 percent lower for the U.S.-only regressions, and 28 percent lower for the regressions for the rest of the world—but the absolute differences in annual average growth rate are substantial as well: 3.95 percent (9.93 percent – 5.98 percent) for the regressions for all nations, 3.52 percent (12.36 percent – 8.84 percent) for the regressions for the rest of the world, and 4.10 percent (7.38 percent – 3.28 percent) for the U.S.-only regressions. We conclude, therefore, that controlling for the clinical trial “quality” characteristics LPATIENTS and SWE results in much lower annual average growth rates and helps explain in part why it is that total grant cost per patient has been increasing steadily over the last two decades.
| Model and phase | Pooled 1989–2011 | 1989–1999 | 2000–2011 | ||
|---|---|---|---|---|---|
| 1989–2011 | 1989–1999 | 2000–2011 | |||
| Base model (1) | |||||
| All | 6.96 | 3.98 | 9.45 | 3.79 | 9.93 |
| U.S. only | 7.01 | 5.80 | 8.01 | 5.70 | 7.38 |
| Rest of world | 8.70 | 6.66 | 10.39 | 6.54 | 12.36 |
| Add SWE and LPATIENTS (1) | |||||
| All | 4.31 | 3.96 | 4.59 | 3.54 | 5.98 |
| U.S. only | 3.62 | 4.28 | 3.07 | 3.92 | 3.28 |
| Rest of world | 6.05 | 6.02 | 6.08 | 5.29 | 8.84 |
| With SWE and LPATIENTS by phase (2) | |||||
| All | |||||
| Phase I | 7.48 | 5.67 | 8.98 | 5.19 | 9.08 |
| Phase II | 6.01 | 6.58 | 5.54 | 6.91 | 5.98 |
| Phase IIIa | 4.04 | 3.88 | 4.18 | 3.25 | 5.16 |
| Phase IIIb | 3.78 | 2.32 | 5.00 | 1.79 | 5.65 |
| Phase IV | 11.91 | 9.25 | 14.13 | 8.17 | 15.75 |
| U.S. only | |||||
| Phase I | 6.78 | 5.72 | 7.66 | 5.07 | 8.58 |
| Phase II | 6.00 | 7.77 | 4.52 | 7.61 | 4.32 |
| Phase IIIa | 3.78 | 4.33 | 3.32 | 3.68 | 2.93 |
| Phase IIIb | 3.48 | 3.92 | 3.11 | 4.24 | 3.34 |
| Phase IV | 6.43 | 8.02 | 5.11 | 7.80 | 4.03 |
| Rest of world | |||||
| Phase I | 15.51 | 11.69 | 18.70 | 10.62 | 23.96 |
| Phase II | 7.64 | 8.48 | 6.95 | 8.65 | 9.52 |
| Phase IIIa | 6.29 | 6.87 | 5.81 | 6.30 | 7.87 |
| Phase IIIb | 12.29 | 15.54 | 9.59 | 13.72 | 11.55 |
| Notes: (1) Underlying regressions also include a constant and indicator variables for therapeutic class and trial phase. (2) Underlying regressions also include a constant and indicator variables for therapeutic class. Based on 207,950 records with total grant cost per patient, PATIENTS, and SWE not missing. The number of observations was 207,950 in the “All” regressions, 118,477 in the “U.S.-only” regressions, and 89,473 in the” Rest of world” regressions. Note: Table entries are the average annual growth rate, over each period, of an hedonic price index constructed from the estimated coefficients on indicator variables for the year in each regression model. (See text.) Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | |||||
The bottom three panels of table 7 report annual average growth rates that come out of separate regressions by trial phase. For pooled 1989–2011 regressions (first column), U.S.-only annual average growth rates are smaller than those resulting from the regressions for all nations over all trial phases and annual average growth rates yielded by the regressions for the rest of the world are greater than those produced by the regressions for all nations for Phases I, II, IIIA, and IIIB, but less than annual average growth rates generated by the regressions for all nations for Phase IV. The variation in growth rates within two sets of regressions is quite large: from 3.78 percent to 11.91 percent in the regressions for all nations and from 6.29 percent to 15.51 percent in the regressions for the rest of the world. A smaller variation—from 3.48 percent to 6.78 percent is seen in the U.S.-only regressions. For all three sets of regressions, annual average growth rates are generally lowest in Phases IIIA and IIIB and mostly highest in Phases II and IV. Even though the regressions involve pooled 1989–2011 data, there is considerable variation across the two subperiods (second and third columns of the table), though less in the U.S.-only regressions than in those for all nations and the rest of the world.
Comparing 1989–1999 annual average growth rates from the pooled regression (second column) with those from the separate 1989–1999 regression (fourth column), and comparing 2000–2011 annual average growth rates from the pooled regression (third column) with those from the separate 2000–2011 regression (last column) provides some evidence regarding the stability of the parameters. The 1989–1999 relative rankings of the annual average growth rates across trial phases (see second and fourth columns for these growth rates) is quite robust, but slightly less so compared with relative rankings obtained from the growth rates listed in the third and fifth columns of the table. Especially notable is the uniformly greatest growth rate from 2000 to 2011 in Phase IV trials, with substantial, but less uniformly large, annual average growth rates in Phase I studies.
| Year | Mean Total Grant Cost per Patient Index | Biomedical R&D Price Index | Pooled hedonic index with trial phase, therapeutic area, and year as indicator variables | Pooled hedonic index with trial phase, therapeutic area, and year as indicator variables and with SWE and LPATIENTS added to base model as regressors |
|---|---|---|---|---|
1989 | 1.000 | 1.000 | 1.000 | 1.000 |
1990 | 1.163 | 1.054 | 1.053 | 1.005 |
1991 | 1.127 | 1.105 | 1.129 | 1.085 |
1992 | 1.202 | 1.154 | 1.141 | 1.063 |
1993 | 1.310 | 1.193 | 1.238 | 1.084 |
1994 | 1.331 | 1.240 | 1.256 | 1.101 |
1995 | 1.363 | 1.282 | 1.291 | 1.144 |
1996 | 1.449 | 1.315 | 1.350 | 1.215 |
1997 | 1.546 | 1.352 | 1.490 | 1.361 |
1998 | 1.844 | 1.398 | 1.869 | 1.636 |
1999 | 1.647 | 1.442 | 1.707 | 1.481 |
2000 | 1.971 | 1.496 | 1.953 | 1.582 |
2001 | 1.836 | 1.545 | 2.020 | 1.623 |
2002 | 1.987 | 1.597 | 2.004 | 1.653 |
2003 | 2.446 | 1.653 | 2.471 | 1.816 |
2004 | 2.930 | 1.714 | 2.801 | 1.783 |
2005 | 2.912 | 1.781 | 2.715 | 1.763 |
2006 | 3.011 | 1.863 | 2.922 | 1.758 |
2007 | 3.097 | 1.934 | 3.338 | 2.187 |
2008 | 3.776 | 2.025 | 3.695 | 1.973 |
2009 | 4.136 | 2.084 | 3.803 | 2.190 |
2010 | 3.757 | 2.144 | 3.752 | 2.122 |
2011 | 4.474 | 2.205 | 4.178 | 2.046 |
Source: Author's calculations based on Medidata Solutions, Inc.'s, PICAS® database. | ||||
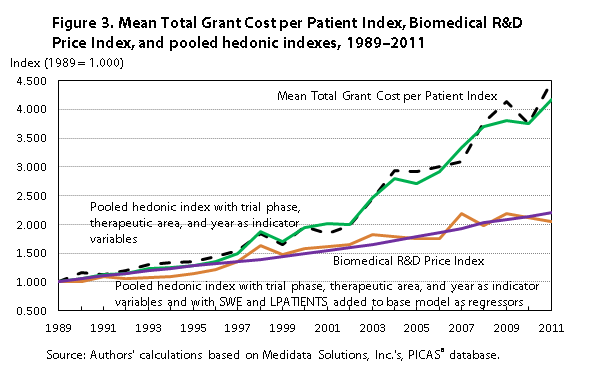
Of particular interest is a comparison of growth rates of (1) price indexes derived from parameters of the base hedonic model including indicator variables for trial phase, therapeutic area, and year; (2) price indexes derived from the augmented hedonic model with SWE and LPATIENTS added to the base hedonic model as regressors; and (3) the Biomedical R&D Price Index published by NIH under contract to BEA (the last based on only NIH-funded research and performed primarily, but not exclusively, at academic medical centers). Figure 3 plots the annual time series of the three price indexes, based on U.S.-only regression estimates for the two hedonic equations, with the normalized series for mean total grant cost per patient included for reference. The results are noteworthy. Indexed to 1.000 in 1989, the Biomedical R&D Price Index is 2.205 in 2011, very close to the augmented hedonic price index value of 2.138, implying similar annual average growth rates and compound annual growth rates over the period: 3.66 percent for both the annual average growth rate and the compound annual growth rate for the Biomedical R&D Price Index, and a 3.63-percent annual average growth rate and a 3.31-percent compound annual growth rate for the augmented hedonic index. By contrast, the 2011 price index derived from the base hedonic model (omitting the SWE and LPATIENTS quality variables) has a value of 4.178, an annual average growth rate of 7.01 percent, and a compound annual growth rate of 6.71 percent. Thus, both the input cost-based Biomedical R&D Price Index and the augmented hedonic model price indexes grow much more slowly—at about one-half the rate of their counterpart indexes derived from the base hedonic model, which controls only for changes in the “mix” of the sample over trial phases and over therapeutic classes.
Tables 8 and 9 present two sets of exploratory findings. Although issues of sample size are likely to become important, we estimate ln(TGPP) equations at the level of the therapeutic class, pooled for 1989–2011 and separately for 1989–1999 and 2000–2011; as before, we estimate regressions on three different geography-based samples: all nations, the United States only, and the rest of the world. The clinical trials in these data involved testing biopharmaceutical treatments for diseases in 14 therapeutic classes, plus a devices-and-diagnostics category. Table 8 reports annual average growth rates by therapeutic class for the U.S.-only and rest-of-the-world regressions; note that, because of the absence of any observations in some years, there is some variability from the 1989–2011, 1989–1999, and 2000–2011 ranges of years, as is described in a footnote to the table. The most striking feature of the table is the substantial variability in the annual average growth rates; not shown is the even greater variability in the estimates for the year indicator variables within each therapeutic class. Although is it likely that there is, in fact, substantial variation in the rate of change of trial costs across therapeutic classes, at least some of the variation is probably attributable to the smaller sample sizes in certain years, resulting from disaggregating into 15 therapeutic classes. In any event, the large variation makes it difficult to estimate the hedonic index values precisely, and, particularly outside the United States, for some therapeutic classes there are only enough observations to estimate the index values in a limited number of years. We conclude that constructing price indexes for clinical trials at the level of therapeutic classes (numbering 15 here) is likely to be infeasible because of sample-size issues, especially for ex-U.S. sites.
| Model and therapeutic class | 1989–2011 | 1989–1999 | 2000–2011 |
|---|---|---|---|
| U.S. only: | |||
| Anti-infective | 4.73 | 0.81 | 7.65 |
| Cardiovascular | 18.64 | 4.95 | 14.10 |
| Central nervous system | 5.05 | 5.00 | 5.35 |
| Dermatology | 6.56 | 9.18 | 2.10 |
| Devices and diagnostics | 17.62 (1) | 18.32 (2) | 22.08 |
| Endocrine | 4.94 | 5.60 | 4.20 |
| Gastrointestinal | 7.11 | 5.77 | 3.14 |
| Genitourinary system | 9.02 | 9.96 | 8.87 |
| Hematology | 11.17 | 25.24 | 2.71 |
| Immunomodulation | 6.08 | 6.77 | 5.82 |
| Oncology | 6.70 | 3.81 | 6.51 |
| Ophthalmology | 9.67 | 8.96 | 21.97 |
| Pain and anesthesia | 10.07 | 9.59 | 11.25 |
| Pharmacokinetics | 6.84 | 5.27 | 8.98 |
| Respiratory system | 8.56 | 5.84 | 12.13 |
| Rest of world: | |||
| Anti-infective | 10.19 | 12.66 | 14.13 |
| Cardiovascular | 15.88 | 13.24 | 13.95 |
| Central nervous system | 9.68 | 6.18 | 13.32 |
| Dermatology | 15.99 (3) | 15.06 | –1.41 |
| Devices and diagnostics | 17.50 (4) | -9.97 (5) | 30.61 (6) |
| Endocrine | 6.10 | 7.66 | 5.83 |
| Gastrointestinal | 20.14 | 3.27 | 23.55 |
| Genitourinary system | 6.58 | 4.75 | 9.01 |
| Hematology | 11.40 (7) | 19.24 | 2.38 (8) |
| Immunomodulation | 13.17 | 18.07 | 12.01 |
| Oncology | 9.60 | 6.39 | 14.40 |
| Ophthalmology | 29.60 | 42.85 | 17.69 |
| Pain and anesthesia | 43.98 (9) | 47.61 | 45.37 |
| Pharmacokinetics | 7.99 (9) | 1.65 | 12.93 (10) |
| Respiratory system | 11.52 | 10.25 | 20.09 (10) |
| Note: Table entries are the average annual growth rate, over each period, of an hedonic price index constructed from the estimated coefficients on indicator variables for the year in each regression model. (See text and notes to table 6.) The number of observations was 118,477 in the “U.S. only” regressions and 89,473 in the “Rest of world” regressions. Because of empty cells, in some cases average annual growth rates are computed over slightly different periods as follows: (1) 1999–2011; (2) 1990–1994; (3) 1990–2003; (4) 1992–1998; (5) 1993–1999; (6) 2009–2011; (7) 1989–2005; (8) 2000–2005; (9) 1989–2006; (10) 2000–2006. Source: Authors’ calculations based on Medidata Solutions, Inc.’s, PICAS® database. | |||
Our final exploratory price index analysis involves aggregating up from individual sites within a given trial to the level at which there is a common protocol. Such aggregation allows us to examine whether the number of sites and the geographical scope of the sites affect the dependent variable, ln(TGPP). The aggregation reduces the number of observations from the 207,950 sites on which the estimates in table 6 are based to 24,172 distinct trials. In pursuit of learning whether the number of sites and the geographical scope of the sites affect ln(TGPP), we construct two new variables that vary at the level of the individual trial protocol (number of sites and number of sites per country) and recalculate the dependent variable and LPATIENTS at the trial level by aggregating the number of patients per site and the total grant cost per site over all sites within each trial before computing TGPP. We have no prior expectation regarding the sign of the coefficient of total number of sites per trial. This coefficient will capture whether or not there are cost impacts of allocating a given number of patients across different numbers of sites. On the one hand, to the extent that fixed costs are incurred at each site for setting up patient recruitment, independently of the number of patients enrolled at a given site, the aggregate TGPP would be expected to increase with the number of sites (in particular, with the number of patients held constant), all other things being equal. On the other hand, if fixed costs are largely trial specific rather than site specific, and if they are carried in the overhead part of trial costs (a condition we do not observe in these data), then they either will not affect site-level costs (i.e., the number of sites will have no observable impact on aggregate TGPP) or, to the extent that they reduce site-specific costs otherwise borne by investigators, will result in a negative relationship between aggregate TGPP and number of sites.
Some of these trial-level fixed costs are likely to be country specific, reflecting factors such as national institutional review boards, import duties and tariffs, medical licensing conventions, or other costs of conforming to a given country’s regulatory framework and medical infrastructure. If these costs are “pushed down” to individual sites, rather than absorbed in the overall overhead cost of the trial, then aggregate TGPP may be affected by the number of sites per country. We therefore also control for each trial’s number of sites per country.
Table 9 reports coefficient estimates for the number of sites and the number of sites per country, for regressions using data pooled over phases (but with phase indicator variables included as regressors) and then for regressions using subsets of the data by each trial phase.44 Pooled over phases, the estimate for number of sites is positive and strongly significant while that for number of sites per country is negative but not significant. Estimated separately by phase, the variable for number of sites is of mixed sign but declines monotonically from early to late phases, although none of the estimates is statistically significant. However, all but one of the estimates for the number of sites per country are positive and, in the case of Phase II and IIIA trials, are statistically significant. Still, in almost all cases the absolute magnitudes of the coefficient estimates are very small—an order of magnitude or smaller than those on the LPATIENTS and SWE variables reported in table 6. We conclude that, at the level of a clinical trial protocol, the number of sites and number of sites per country do not appear to have a material effect on the total grant cost per patient. These trial characteristics might, however, have varying effects on the sponsors’ overall “headquarters” overhead costs, but if so, they are effects we do not observe.
| Variable | Number of sites | Number of sites per country | Observations |
|---|---|---|---|
| Pooled over phases | 0.0016 (1) | –0.0010 | 24,172 |
| By phase: | |||
| Phase I | 0.0223 | 0.0102 | 5,557 |
| Phase II | 0.0012 | .0051 (1) | 5,775 |
| Phase IIIa | 0.0004 | .0016 (2) | 8,953 |
| Phase IIIb | –.0008 | 0.0005 | 1,735 |
| Phase IV | –.0021 | –.0013 | 2,152 |
| Notes: (1) Statistically significant at p < .01. (2) Statistically significant at p < .10. Note: Based on 24,172 trials for which site work effort and total grant cost were not missing. The trial level was computed on the basis of total grant cost per site, aggregated over all sites in the trial, divided by the total number of patients aggregated over all sites. Table entries are estimated regression coefficients of the explanatory variables “Number of sites” and “Number of sites per country” observed for each trial. In addition to these variables, the “Pooled over phases” regression includes (1) a constant, (2) the natural logarithm of the total number of patients over all sites, (3) site work effort, and (4) indicator variables for therapeutic class, trial phase, and year, while the “By phase” regressions also include (1) a constant, (2) the natural logarithm of the total number of patients over all sites, (3) site work effort, and (4) indicator variables for therapeutic class and year. | |||
One important practical issue with hedonic indexes such as those estimated in the previous section is that of updating and revising the indexes: over time, as new data are acquired, statistical agencies that are reestimating the pooled regression model for the expanded and updated dataset will likely find changes in the estimated time dummy coefficients and thus in the historical hedonic price index values derived from them. Revising historical time series of price indexes each time a new period is added is an unattractive feature of the pooled hedonic price index methodology. One way to avoid this problem is to construct an index that is based on results from a set of sequentially estimated “adjacent year” regressions: for any year t, use data only for years t and t – 1 to estimate the model, with the coefficient of a dummy variable for year t providing an estimate of the change in a “quality-adjusted” (i.e., characteristics-adjusted) index over the two periods. Year-on-year changes can be then be chained to create an index for the whole period.
Focusing on the U.S.-only sample, we find that indexes constructed with this method track the hedonic index estimated from the pooled sample quite closely. For the “base” model that controls only for phase and therapeutic class, the annual average growth rate of the adjacent-years index is 7.47 percent, compared with the 7.01 percent for the pooled hedonic index (and 7.52 percent for the mean nominal total grant cost per patient). For the hedonic models that include SWE and LPATIENTS, the annual average growth rate for the adjacent-year index is 3.73 percent, compared with 3.62 percent for the pooled hedonic index. (Recall that the annual average growth rate for the Biomedical R&D Price Index is 3.66 percent.) These results reflect remarkably similar growth rates based on alternative price index methodologies over almost a quarter of a century. Although a formal statistical test rejects equality of the coefficients of all the variables across all pairs of adjacent years, visual examination of the coefficients in each of the adjacent-year regressions (not presented here) shows them to be quite stable over time.
An even more general alternative approach to estimating the constant-characteristics change in price 45 is to estimate regression coefficients separately for each year and then use alternative fixed-quantity (characteristic) weights to compute Paasche-style or Laspeyres-style index ratios. For example, if Xi0 are the characteristics for each observation in year 0, ß0 are hedonic coefficients estimated from the year-0 regression, and Xi1 and ß1 are, respectively, the characteristics for each observation and the hedonic coefficients estimated for year 1, then a Laspeyres-type measure of the constant-characteristics change in prices can be calculated as L1 = (Σi Xi0 ß1)/(Σi Xi0ß0) and the corresponding Paasche-type index as P1 = (Σi Xi1ß1)/(Σi Xi1ß0), with the Fisher Ideal index given by F1 = (L1P1)½.
The advantage of this method over the adjacent-years dummy-variable method is that in the adjacent-year regressions the only parameters that is allowed to vary between the two adjacent years is the year dummy variable, whereas in the pure hedonic method all coefficient estimates (interpreted as shadow prices of the characteristics) can change between years. In the pure hedonic method, these yearly shadow prices are weighted by fixed weights—either the base-period (Laspeyres) or the current-period (Paasche) characteristics.
A potential problem with the chained indexes L1 and P1 is “drift.” If relative prices “bounce” (repeatedly move upward and downward) over a multiyear period, then negative autocorrelations in prices, combined with negative correlations between changes in price and changes in quantity, can generate an upward “drift” in the chained L1 index and a downward “drift” in the chained P1 index.46 Although the theoretical foundations have, to the best of our knowledge, not been established, it is possible that a superlative chained Fisher Ideal index that is the geometric mean of a chained Laspeyres and chained Paasche index would embody offsetting drifts, thereby resulting in a more reliable chained index than either the Laspeyres or Paasche index alone.
| Year | Adjacent-years hedonic | Pooled time-dummy hedonic | Biomedical R&D Price Index | Pure hedonic: Laspeyres | Pure hedonic: Paasche | Pure hedonic: Fisher Ideal |
|---|---|---|---|---|---|---|
1989 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
1990 | .931 | 1.053 | 1.054 | .944 | .949 | .946 |
1991 | 1.030 | 1.129 | 1.105 | 1.042 | 1.054 | 1.048 |
1992 | 1.032 | 1.141 | 1.154 | 1.013 | .998 | 1.005 |
1993 | 1.033 | 1.238 | 1.193 | 1.038 | 1.008 | 1.023 |
1994 | 1.050 | 1.256 | 1.240 | 1.113 | 1.054 | 1.083 |
1995 | 1.103 | 1.291 | 1.282 | 1.132 | 1.070 | 1.101 |
1996 | 1.198 | 1.350 | 1.315 | 1.208 | 1.129 | 1.168 |
1997 | 1.349 | 1.490 | 1.352 | 1.377 | 1.278 | 1.327 |
1998 | 1.578 | 1.869 | 1.398 | 1.641 | 1.539 | 1.590 |
1999 | 1.430 | 1.707 | 1.442 | 1.503 | 1.380 | 1.440 |
2000 | 1.491 | 1.953 | 1.496 | 1.568 | 1.435 | 1.500 |
2001 | 1.488 | 2.020 | 1.545 | 1.570 | 1.435 | 1.501 |
2002 | 1.539 | 2.004 | 1.597 | 1.652 | 1.472 | 1.559 |
2003 | 1.591 | 2.471 | 1.653 | 1.830 | 1.496 | 1.655 |
2004 | 1.635 | 2.801 | 1.714 | 2.033 | 1.492 | 1.742 |
2005 | 1.589 | 2.715 | 1.781 | 2.102 | 1.507 | 1.780 |
2006 | 1.632 | 2.922 | 1.863 | 2.150 | 1.525 | 1.811 |
2007 | 1.786 | 3.338 | 1.934 | 2.418 | 1.625 | 1.982 |
2008 | 1.865 | 3.695 | 2.025 | 2.604 | 1.639 | 2.066 |
2009 | 2.182 | 3.803 | 2.084 | 2.921 | 1.754 | 2.263 |
2010 | 2.072 | 3.752 | 2.144 | 2.759 | 1.703 | 2.168 |
2011 | 2.138 | 4.178 | 2.205 | 3.033 | 1.627 | 2.221 |
Source: Author's calculations based on Medidata Solutions, Inc.'s, PICAS® database. | ||||||
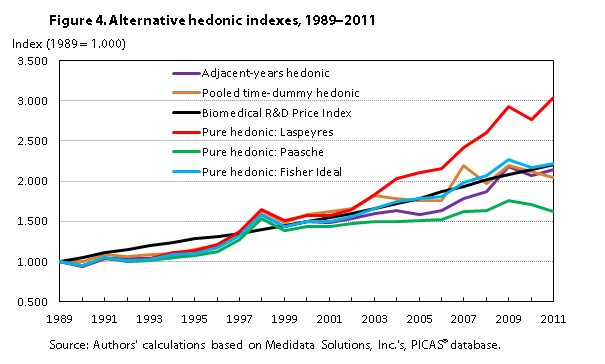
Results obtained from calculating these indexes and chaining for all years in the U.S.-only sample are broadly consistent with the results obtained from the adjacent-years method. For the regression specification that includes SWE and LPATIENTS, the annual average growth rates were 5.40 percent for a Laspeyres-type pure hedonic index, 2.44 percent for a Paasche-type pure hedonic index, and 3.89 percent for the Fisher Ideal pure hedonic index. Figure 4 plots the various hedonic indexes (based on the augmented regression) examined. The figure shows that the pooled hedonic, adjacent-years hedonic, and pure hedonic Fisher Ideal indexes track each other (and the Biomedical R&D Price Index). Values of these four indexes are remarkably close to one another for 2011: 2.046 for the pooled hedonic index, 2.138 for the adjacent-years hedonic index, 2.221 for the pure hedonic Fisher Ideal index, and 2.205 for the Biomedical R&D Price Index. Also, the four indexes have similar annual average growth rates (3.62 percent, 3.73 percent, 3.89 percent, and 3.66 percent, respectively) and similar compound annual growth rates (3.31 percent, 3.52 percent, 3.69 percent, and 3.66 percent, respectively). In contrast, the chained pure hedonic Paasche index (with potential downward drift) has 2011 values well below those of the other four indexes (just 1.627, with an annual average growth rate of 2.40 percent and a compound annual growth rate of 2.24 percent), and the chained pure hedonic Laspeyres index (with possible upward drift) has 2011 values well above those of the other four indexes (3.033, with an annual average growth rate of 5.40 percent and a compound annual growth rate of 5.17 percent).
The close correspondence among the results obtained for all three hedonic index methods (pooled time dummy, adjacent-years time dummy, and pure hedonic) suggest that the underlying relationship between the observed nominal transaction prices and the key characteristics of each contract (SWE, LPATIENTS, phase, and therapeutic class) is quite robust, at least within the U.S.-only sample. It would therefore appear to be reasonable to use either the pure hedonic Fisher Ideal or the adjacent-year time dummy method with U.S. data to develop a periodically updated index.
Expenditures on clinical trials undertaken to develop new drugs have increased dramatically over the past 30 years. To better understand the underlying causes, it is critical to be able to decompose increases in total spending into a price effect, a quantity effect, and a “quality” effect. Are biopharmaceutical companies doing more clinical research, has the cost of doing a given amount of research increased, or are both phenomena occurring? This article has focused on the unit costs of certain aspects of conducting clinical trials. These costs have risen substantially in recent decades, outpacing general inflation and other measures of changes in the costs of other inputs to biomedical R&D. Our results suggest that the increases seen in trial costs are attributable not solely to changes in input costs such as wages and the cost of equipment and facilities; they also appear to have been driven to a substantial extent by two other phenomena: smaller numbers of patients per site and increases in the level of effort required by investigators with the establishment of study protocols that now require more costly and complex monitoring and testing of subjects. Evaluated at the sample means, our estimated elasticity of total grant cost per patient with respect to site work effort is about 0.5. Over the 1989–2011 period, mean values of site work effort have varied by as much as a factor of 3, generally rising, but not quite monotonically, over time. (See table 1.) This behavior suggests that the increased intensity of effort required of investigators in implementing trial protocols (in the form of more demanding medical procedures and, potentially, greater complexity of trial designs) has been a major driver of the increase in nominal total grant cost per patient, over and above changes in input costs. By comparison, our estimates of the elasticity of total grant cost per patient with respect to the number of patients per site is much smaller in absolute magnitude (about –0.120 for the U.S.-only sample; see table 6), and because the relative decrease in patients over time is smaller than the relative increase in site work effort, declining site size is not as large a driver of increases in total grant cost per patient as are changes in site work effort. Thus, although the trends in site work effort and number of patients per site are in turn likely driven to some extent by cost differences across therapeutic classes and phases of clinical development, the estimated effects we find are obtained with such study characteristics controlled for and are not just an artifact of changes in the composition of the sample. The size of those effects implies that any effort to track costs of clinical research should pay close attention to the nature of study protocols and the organization and management of trials. The extent to which increases in site work effort are attributable to increased regulatory requirements and scrutiny versus evolving commercial product differentiation strategies is unknown and merits further analysis. Our findings point to the value of using the hedonic regression methodology in this context.
It is important to note that we are not estimating an R&D output price index, such as might be developed to allow a decomposition of changes in the cost per new drug into price and quantity components. The output of the activity we study is clinical data on patient outcomes; such output constitutes increments to scientific knowledge about the disease and drug being investigated. We do not observe the use of these outputs in creating final products (new drugs), and the indexes we compute should be understood more properly as an input cost index for one component of purchased R&D services, which are an intermediate input into the activity of creating new drugs.
The price indexes for commercial clinical research constructed here appear to behave remarkably similarly to those published by NIH under contract to BEA for input costs for public sector biomedical R&D, once one controls for site work effort and investigator total grant cost per patient in the commercial trials; this unexpected congruence merits more careful attention and confirmation by government statistical agencies and other entities with an interest in tracking biomedical R&D costs in the public sector. Specifically, the annual average growth rate of a price index that controls only for therapeutic class and phase of development rises almost twice as fast as the NIH Biomedical R&D Price Index. But interestingly, once the scale of investigator or site activity and the effort required by a study protocol are also taken into account, the estimated “quality-adjusted” rate of inflation within the United States is remarkably similar to that of the Biomedical R&D Price Index. This similarity suggests that increases in commercial clinical trial costs are driven primarily by changes in the nature of clinical research rather than by inflation in input costs.
Commercial databases such as the one we have used in this article appear to have great potential as a source of data for price index measurement purposes, particularly if restricted to the U.S. context. With these data, it would appear to be feasible to compute measures of price inflation for this aspect of clinical research, to do so separately for different phases of clinical development, and to do so for some, but not all, therapeutic classes. Our results suggest quite significant differences in rates of inflation across different therapeutic classes, even after controlling for observable characteristics, but understanding the underlying causes of this heterogeneity will require more detailed investigation and, likely, more detailed data from other sources. The geographic reach of these data sources also presents interesting opportunities to benchmark R&D costs across different regions within the United States, as well as across countries. However, care needs to be taken to ensure that the number of observations is adequate: even with the very large dataset we have used, cell counts at the level of therapeutic class, region, and year may be too small to allow reliable estimation.
There are some important limitations to this study. Chief among them is that we look at only one component of trial costs: payments to clinical investigators. In our dataset, these account for about one-half of the total cost of a trial. It may well be that some of the higher per-patient costs created by having fewer patients per site and increased effort required by the protocol are offset by savings in the sponsors’ headquarters’ costs of centralized administration and coordination of trials that we do not observe here. Limited or delayed availability of data prevents us from drawing strong conclusions about trends in total trial costs and underlying factors in the most recent years in the sample. As noted earlier, the prices we observe are only for the payments made by the trial sponsor to investigators, either directly or through a CRO, and additional costs for trial design and administration are not included. Thus, on the one hand, to the extent that these additional overhead costs are understood as internal headquarters costs of the entity purchasing the R&D output of trial sites, our focus on investigator contracts has the appropriate scope for purposes of developing a PPI for contracted R&D services. On the other hand, if the costs of trial design and administration are understood as R&D costs, then our focus may be too narrow. In many instances, and increasingly over time, trial sponsors contract with a CRO to perform some or all of these functions, and such payments may well be considered part of the contracted R&D services. The issue of understanding the nature of overhead costs warrants further investigation, but would require additional data on the nature of payments by trial sponsors to CROs, as well as the development of a linkage between these contracts and the investigator payments analyzed here. In this context, it is unclear how well the site work effort measure used here captures differences in the burden imposed by, for example, running more complex trial protocols in which some of the overhead associated with management and administration is being borne by the site, as opposed to the sponsor or CRO, as distinct from the increased use of more costly interventions or methods of measuring trial end points.
Although we have not been able to evaluate the representativeness of the clinical trial investigator contracts in our sample relative to the underlying population of all such agreements, we have no reason to believe that the sample is unrepresentative, and the distribution of studies across development phases and therapeutic classes and countries in the sample does not diverge markedly from that seen in public trial registries such as clinicaltrials.gov, at least for the years since these registries have become well populated. But we are not able to evaluate whether participation in Medidata’s data-gathering process is nonrandom relative to the population of potential participants and, if so, whether nonrandom sampling will induce any significant degree of bias into the results—although, given the close correspondence between the “quality-adjusted” indexes and the Biomedical R&D Price Index, which is computed with the use of weights derived from an independent sampling method, bias due to nonrandom sampling seems quite unlikely. Last, because the identities of study sponsors and investigators were not available to us, we were not able to investigate either differences in costs across, for example, trials sponsored by large versus small commercial entities or any instances of in which public sector agencies or nonprofit organizations, rather than industry, were sponsors or investigators of trials.
ACKNOWLEDGMENT: Research support from the National Science Foundation for the award titled “Collaborative Research: TLS: An Experimental Producer Price Index for Clinical Trials” to the National Bureau of Economic Research, Award Number 0915674, and Boston University, Award Number 0915677, is gratefully acknowledged. We thank Medidata Solutions, Inc. (“Medidata”), for supplying database extracts; Ed Seguine, Rafael Campo, and other individuals at Medidata for helpful discussions, comments, and data support; and Marshall Reinsdorf from the Bureau of Economic Analysis for constructive discussant’s comments at the Annual Meetings of the American Economic Association in San Diego, California, January 6, 2013. Rania Gihleb, Ph.D. candidate, Department of Economics, Boston University, provided able research assistance. The opinions expressed herein are those of the authors and do not necessarily reflect opinions of the National Science Foundation, Medidata, or the institutions with which the authors are affiliated.
Ernst R. Berndt, and Iain M. Cockburn, "Price indexes for clinical trial research: a feasibility study," Monthly Labor Review, U.S. Bureau of Labor Statistics, June 2014, https://doi.org/10.21916/mlr.2014.22
1 Although the United States has long led the world in combined government and industry spending on R&D, in recent years Asian economies have increased their R&D-to-GDP intensity, resulting in R&D levels that have gained considerable ground on the U.S level. One estimate has 2012 U.S. R&D expenditures of $418.6 billion and an R&D–GDP ratio of 2.68 percent, while the comparable figures for China are $197.3 billion and 1.60 percent and for Japan are $159.9 billion and 3.48 percent. Other countries with 2012 R&D–GDP ratios greater than 3 percent are Finland at 3.80 percent; Sweden, 3.62 percent; South Korea, 3.45 percent; and Denmark, 3.08 percent. (See “R&D spending growth continues while globalization accelerates,” 2012 Global R&D funding forecast (Columbus, OH: Battelle Institute & R&D Magazine, December 2011), pp. 3–5, especially p. 5, http://www.battelle.org/docs/default-document-library/2012_global_forecast.pdf.)
2 Jennifer Lee and Andrew G. Schmidt, “Research and development satellite account update: estimates for 1959–2007,” Survey of Current Business (U.S. Department of Commerce, Bureau of Economic Analysis, December 2010), pp. 16–27.
3 Industry performs about 71 percent of R&D in the nation. (See “Stable growth of U.S. R&D,” 2012 Global R&D funding forecast, pp. 6–8, especially p. 6.)
4 David Friedman, “Developing a PPI for scientific research and development: NAICS 5417/ISIC 7310,” slide presentation held at the 25th Meeting of the Voorburg Group, Vienna, Austria, September 23, 2010 (see especially slide 6), http://stds.statcan.ca/english/voorburg/Documents/2010%20Vienna/Papers/2010%20-%2081.pdf. (See also Adam Copeland and Dennis Fixler, “Measuring the price of research and development output,” paper presented at the National Bureau of Economic Research Summer Institute Productivity Program, July 2008, https://www.bea.gov/papers/pdf/MeasuringthePriceofRDcurrent.pdf; and Adam Copeland, Gabriel W. Medeiros, and Carol A. Robbins, “Estimating prices for R&D investment in the 2007 R&D satellite accounts,” BEA Background Paper (U.S. Department of Commerce, Bureau of Economic Analysis, November 2007), https://www.bea.gov/papers/pdf/Estimation_of_prices_final.pdf.)
5 Friedman, “Developing a PPI,” slide 6.
6 Ibid., slide 5.
7 2011 profile: pharmaceutical industry (Washington, DC, Pharmaceutical Research and Manufacturers of America, 2011). Expenditures on Phase 1 trials were $3.753 billion; on Phase 2, $7.124 billion; on Phase 3, $16.300 billion; and on Phase 4, $5.303 billion. (See appendix table 5, p. 45).
8 See Funding: funding facts, NIH Research Portfolio Online Reporting Tools (RePORT) (U.S. Department of Health and Human Services, National Institutes of Health, June 3, 2013), http://report.nih.gov/fundingfacts/fundingfacts.aspx .
9 The business model of CROs has evolved from providing “transactional” capacity for resource-constrained drug developers to a model oriented toward longer term strategic partnerships and “preferred provider” status. (See, e.g., Strategic partnering: CRO evolution (Covance), http://www.covance.com/products/strategic-partnering/cro-evolution.php .) By the middle of the first decade of the 21st century, estimates of the fraction of development spending outsourced to CROs approached 30 percent. (See Jefferies & Company, cited in PAREXEL’s Bio/pharmaceutical statistical sourcebook, 2006/2007 (Waltham, MA: PARAXEL International, Inc., 2006).)
10 See Pierre Azoulay, “Capturing knowledge within and across firm boundaries: evidence from clinical development,” American Economic Review, December 2004, pp. 1591–1612, http://pazoulay.scripts.mit.edu/pubs/knowledge.pdf ; Pierre Azoulay and Ariel Fishman, “Doctors, $$ and drug development: the rise of for-profit experimental medicine,” paper presented at the National Bureau of Economic Research Location of Biopharmaceutical Activity Conference, Savannah, GA, March 7–8, 2008, available from pazoulay@mit.edu.
11 See, for example, Fabio Thiers, Anthony J. Sinskey, and Ernst R. Berndt, “Trends in the globalization of clinical trials,” Nature Reviews: Drug Discovery, January 2008, pp. 13–14.
12 Pierre Azoulay, “The changing economics of clinical development,” slide presentation held at the Earth Institute, Columbia University, New York, NY, May 20, 2004 (see especially slide 7), available from pazoulay@mit.edu.
13 Roslyn Swick, Deanna Bathgate, and Michael Horrigan, “Services producer price indices: past, present, and future,” paper presented at the 10th meeting of the Federal Economic Statistics Advisory Committee, Washington, DC, June 9, 2006.
14 For details on the construction of the Biomedical R&D Price Index, see James Schuttinga, “The Biomedical Research and Development Price Index,” PowerPoint presentation for MIT economists, March 25, 2008; and “Price indexes” (U.S. Department of Health and Human Services, National Institutes of Health, updated periodically), http://officeofbudget.od.nih.gov/gbiPriceIndexes.html (click on link “BRDPI overview of annual update”).
15 “Biomedical Research and Development Price Index (BRDPI): fiscal year 2010 update and projections for FY 2011–FY 2016” (U.S. Department of Health and Human Services, National Institutes of Health, January 24, 2011), p. 1, http://officeofbudget.od.nih.gov/pdfs/FY12/BRDPI_Proj_Jan_2011_Final.pdf.
16 Total R&D spending by PhRMA member companies was $26.0 billion in 2000 and $49.4 billion in 2010, an increase of 90 percent. (See 2011 profile: pharmaceutical industry, Appendix Table 1, p. 42.)
17 The total NIH budget obligation in fiscal year 2000 was $l7.8 billion, and in fiscal year 2010 it was $31.0 billion, an increase of 74 percent. (See “National Institutes of Health: history of congressional appropriations, fiscal years 2000–2013 (National Institutes of Health, Office of Budget), http://officeofbudget.od.nih.gov/pdfs/FY15/Approp%20%20History%20by%20IC%20through%20FY%202013.pdf .)
18 Joseph A. DiMasi, Ronald W. Hansen, and Henry G. Grabowski, “The price of innovation: new estimates of drug development costs,” Journal of Health Economics, March 2003, pp. 151–185.
19 Kenneth A. Getz, Julia Wenger, Rafael A. Campo, Eward S. Seguine, and Kenneth I. Kaitlin, “Assessing the impact of protocol design changes on clinical trial performance,” American Journal of Therapeutics,September/October 2008, pp. 450–457.
20 See, for example, the highly influential studies by David Cutler and coauthors on the costs of treating heart attacks. These studies have had a major impact on analyses of health expenditures, focusing attention on changes in the cost of an “episode of care” due to input substitution, rather than on changes in the per-unit price of inputs to care. (See, e.g., David M. Cutler, Mark McClellan, Joseph P. Newhouse, and Dahlia Remler, “Are medical prices declining? Evidence from heart attack treatments,” Quarterly Journal of Economics, November 1998, pp. 991–1024; David M. Cutler and Mark B. McClellan, “What is technological change?” in David Wise, ed., Inquiries in the economics of aging (Chicago: University of Chicago Press, 1998); and David M. Cutler and Mark McClellan, “Is technological change in medicine worth it?” Health Affairs, September 2001, pp. 11–29.)
21 See, for example, Ernst R. Berndt and Neal J. Rappaport, “Price and quality of desktop and mobile personal computers: a quarter century historical overview,” American Economic Review, May 2001, pp. 268–273 and the references cited therein.
22 For a more detailed discussion, see Charles L. Schultze and Christopher Mackie, eds., At what price? Conceptualizing and measuring cost-of-living and price indexes/Panel on Conceptual, Measurement, and Other Statistical Issues in Developing Cost-of-Living Indexes (Washington, DC: National Academy Press, 2002), chapter 4, “Evolving market baskets: adjusting indexes to account for quality change.”
23 Azoulay, “The changing economics”; and Azoulay and Fishman, “Doctors, $$ and drug development.”
24 We thank Marshall Reinsdorf, who read and discussed a previous version of this article, for suggesting the third investigation. The method we utilize was presented in Ariel Pakes, “A reconsideration of hedonic price indexes with an application to PCs,” American Economic Review, December 2003, pp. 1578–1614; and Ernst R. Berndt, Zvi Griliches, and Neal J. Rappaport, “Econometric estimates of price indexes for personal computers in the 1990s,” Journal of Econometrics, July 1995, pp. 243–268.
25 In a clinical trial, a “site” is the administrative unit—typically a hospital, clinic, or physician office—enrolling subjects.
26 The average annual growth rates cited in this article are the arithmetic means of year-over-year growth rates; the compounded average annual growth rate is slightly less, at 7.0 percent; see also note 42.
27 In the somewhat larger sample (245,803 records) that includes contracts in which the number of patients is not specified, the figures are similar: the mean total grant cost per patient rose from $3,752 to $15,567 at an average annual growth rate of 7.1 percent.
28 “Biomedical Research and Development Price Index (BRDPI): Fiscal Year 2010,” Supplemental Table A, p. 6.
29 RVUs are measures constructed by Medicare to estimate the relative level of physician time, skill, training, and expertise that Medicare relies upon to establish payment levels for physicians’ services.
30 For further details, see Getz, Wenger, Campo, Seguine, and Kaitlin, “Assessing the impact of protocol design changes.”
31 Coefficients of site work effort in regressions estimated from site-level data should be interpreted accordingly. Note that standard errors in these regressions were computed on the basis of clustering by protocol.
32 Similar figures are obtained for the slightly larger set of protocols for which the investigator contracts do not specify the number of patients at a site or from a reweighting of the protocol-level statistics by the number of contracts per protocol.
33 For a historical overview of hedonichedonic price analysis, see Ernst R. Berndt, The practice of econometrics: classic and contemporary (Reading, MA: Addison-Wesley, 1991), chapter 4. (See also Berndt, Griliches, and Rappaport, “Econometric estimates of price indexes”; and Berndt and Rappaport, “Price and quality of desktop and mobile personal computers.”)
34 For further discussion, see Berndt,The practice of econometrics, chapter 4; and Jack E. Triplett, Handbook on hedonic indexes and quality adjustment in price indexes: special application to information technology products (Paris: Organisation for Economic Co-operation and Development, 2006).
35 Applications are primarily in modeling health care costs and outcomes. (See, e.g., Naihua Duan, “Smearing estimate: a nonparametric retransformation method,” Journal of the American Statistical Association, vol. 78, no. 383, 1983, pp. 605–610; Willard G. Manning and John Mullahy, “Estimating log models: to transform or not to transform?” Journal of Health Economics, July 2001, pp. 461–494; Willard G. Manning, “The logged dependent variable, heteroskedasticity, and the retransformation problem,” Journal of Health Economics, June 1998, pp. 283–295; and John Mullahy, “Much ado about two: reconsidering retransformation and the two-part model in health econometrics,” Journal of Health Economics, June 1998, pp. 247–281.)
36 See Triplett, Handbook on hedonic indexes and quality adjustment in price indexes, p. 34, footnote 41.
37 See Duan, “Smearing estimate.”
38 Note that if the logarithm of the total grant amount, rather than total grant per planned number of enrolled patients, were the dependent variable (i.e., if LPATIENTS was not part of the dependent variable) while LPATIENTS was a regressor, then, by the arithmetic of least squares and logarithms, the coefficient of LPATIENTS would numerically be 1.0 plus the estimate of LPATIENTS in the log(TGPP) estimation. Thus, our results on scale economies are numerically robust whether or not LPATIENTS is part of the dependent variable. (Note that using log(SWE) in place of SWE does not change the sign or statistical significance of the estimated site work effort–related coefficient or result in material differences in the other estimates.)
39 In all models, tests of the joint null hypothesis that estimated coefficients of site work effort, of LPATIENTS, and of the various indicator variables were stable over the two subperiods were decisively rejected.
40 Pooled over time, the number of observations in the top-panel regressions in table 6 is 207,950 (all), 118,477 (United States only), and 89,473 (rest of world); for the 1989–1999 (2000–2009) regressions, the corresponding numbers of observations are 125,736 (82,217), 66,246 (52,231), and 59,490 (29,983). Of course, the number of observations in the various regressions by phase is smaller, with the smallest number being 2,738 for the 2000–2011 Phase I regressions.
41 The logarithm transform is used for patients because of the high degree of skewness and the wide range of that variable. Site work effort falls into a much tighter range: no substantial differences in the results were obtained with the logarithm.
42 The significance levels found were computed with the use of standard errors clustered by protocol to address the possible downward bias induced by the inclusion of protocol-level site work effort and phase dummies as “aggregate regressors.” (See Brent Moulton, “Random group effects and the precision of regression estimates,” Journal of Econometrics, vol. 32, no. 3, 1986, pp. 385–397.)
43 These arithmetic annual average growth rates were more stable than were estimates of compounded average growth rates, because the latter were sensitive to the choice of initial and end-year periods.
44 SWE, LPATIENTS, and year and therapeutic class indicators are also included in the regressions. Estimated coefficients on SWE and LPATIENTS were similar in magnitude to those obtained in the site-level regressions and were statistically significant at the 1-percent level.
45 Sometimes known as the pure hedonic method; see Pakes, “A reconsideration of hedonic price indexes,” and Berndt, Griliches, and Rappaport, “Econometric estimates of price indexes.”
46 For a discussion of drift in the context of alternative direct and chained index numbers, see Bohdan J. Szulc, “Linking price index numbers,” in W. Erwin Diewert and Claude Montmarquette, eds., Price level measurement: proceedings from a conference sponsored by Statistics Canada (Ottawa: Ministry of Supply and Services Canada, December 1983), pp. 537–566.