An official website of the United States government
 United States Department of Labor
United States Department of Labor

Crossref 0
Wage Disparities in Academia for Engineering Women of Color and the Limitations of Advocacy and Agency, Research in Higher Education, 2024.
Chapter 11 : Built Environment, Urban Systems, and Cities. Impacts, Risks, and Adaptation in the United States: The Fourth National Climate Assessment, Volume II, Chapter 11 : Built Environment, Urban Systems, and Cities. Impacts, Risks, and Adaptation in the United States: The Fourth National Climate Assessment, Volume II, 2018.
The Impact of Technology on Wages in Non-Standard Employment, Reskilling the Workforce in the Labor Market, 2024.
Global Cities and Socioeconomic Inequality: A Pathways Inquiry, SSRN Electronic Journal , 2020.
This article shows that location, size, and occupational composition play important roles in determining the level of wage inequality within and across U.S. metropolitan areas. Larger areas, especially in the Northeast and on the West Coast, typically have greater wage inequality, while smaller areas, many of which are in the South and Midwest, have less inequality. Metropolitan areas with high concentrations of employment in higher paying occupations also tend to have greater inequality.
Rising wage inequality in recent years has brought increased focus on the disparity between the highest wage earners and the lowest wage earners. Less attention, however, has been paid to how wage inequality varies by location or area. By one measure—the ratio of the 90th wage percentile to the 10th wage percentile, sometimes called the “90–10” ratio, inequality increased by 7 percent in the United States between 2003 and 2013. But this increase varied widely by area. The 90–10 ratio increased by over 20 percent in Oakland, CA, and Corvallis, OR, for example, while it declined in several other metropolitan areas in the United States, including three areas in Florida. This article examines how wage inequality varies by metropolitan area and how average wages, occupational composition, geographic location, and the size of the area contribute to the variation in this inequality measure.
The data used in this article are from the Occupational Employment Statistics (OES) program. The OES program produces employment and wage estimates annually for more than 800 occupations. These data are available for the nation as a whole, for individual states, and for metropolitan and nonmetropolitan areas; national occupational employment and wages for specific industries are also available. The most recent data show that the 90th-percentile annual wage in the United States for all occupations combined was $88,330 in 2013, and the 10th-percentile wage was $18,190. In other words, the highest paid 10 percent of wage earners in the United States earned at least $88,330 per year, while the lowest paid 10 percent earned less than $18,190 per year. Therefore, by this measure, the “90–10” ratio in the United States was 4.86 in 2013, compared with 4.54 in 2003, an increase of about 7 percent over that 10-year period.
Differences in the 90–10 ratio over time or geography can be due to several factors. They may result from differences in wages for the highest paid workers, the lowest paid workers, or both groups. Differences in the 90th and 10th wage percentiles may also be the result of differences in wage levels within the same occupations, differences in the occupational makeup of the area or areas, or some combination of both. Finally, changes in wage inequality may be because the wages of the highest paid 10 percent of workers (those with wages at or above the 90th percentile) grew faster than those of the lowest paid 10 percent (those whose wages fall below the 10th percentile). In fact, between 2003 and 2013, after adjusting for inflation, the 90th-percentile wage increased 4.6 percent while the 10th-percentile wage decreased 2.2 percent. Figure 1 shows the change in real annual wages at the national level for the 10th, 25th, 50th (median), 75th, and 90th percentiles over the 2003–13 period. As can be seen in the figure, in general, real annual wages increased for the highest paid workers and decreased for the lowest paid workers, a pattern that holds for most metropolitan areas. Nominal wages for both measures increased, but the 90th percentile grew faster than the 10th percentile. This pattern holds for most, but not all metropolitan areas. The remainder of this article examines nominal wages by metropolitan area.
| Percentile | Percent change |
|---|---|
| 10th percentile | -2.2 |
| 25th percentile | -5.5 |
| 50th percentile | -1.8 |
| 75th percentile | 1.7 |
| 90th percentile | 4.6 |
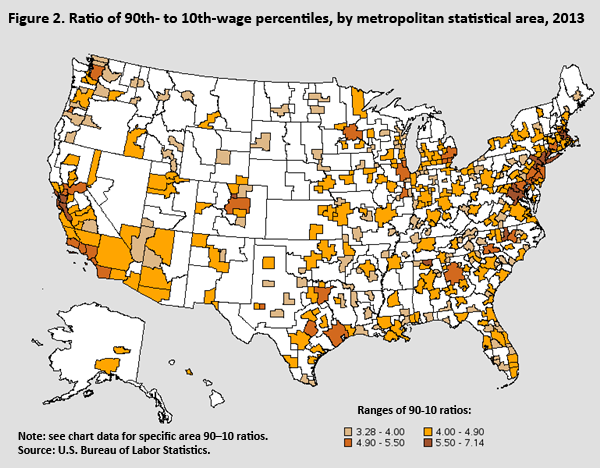
Wage inequality varies considerably by metropolitan area. For example, San Jose-Sunnyvale-Santa Clara, CA, had the largest 90–10 ratio, at 7.14, while Morristown, TN, had the lowest ratio, at 3.28. Figure 2 shows how the 90–10 ratio varies by metropolitan statistical area (MSA). The largest
| Area | 90–10 ratio | Employment |
|---|---|---|
| San Jose-Sunnyvale-Santa Clara, CA | 7.14 | 930,070 |
| Washington-Arlington-Alexandria, DC-VA-MD-WV | 6.76 | 2,367,240 |
| Bethesda-Rockville-Frederick, MD | 6.29 | 561,830 |
| New York-White Plains-Wayne, NY-NJ | 6.28 | 5,242,070 |
| Huntsville, AL | 6.16 | 210,110 |
| San Francisco-San Mateo-Redwood City, CA | 6.15 | 1,045,700 |
| Oakland-Fremont-Hayward, CA | 6.03 | 1,003,860 |
| Bridgeport-Stamford-Norwalk, CT | 6.00 | 420,170 |
| Durham-Chapel Hill, NC | 5.76 | 276,580 |
| Boulder, CO | 5.68 | 163,010 |
| Boston-Cambridge-Quincy, MA | 5.63 | 1,748,940 |
| Nassau-Suffolk, NY | 5.62 | 1,235,610 |
| Newark-Union, NJ-PA | 5.58 | 957,630 |
| Framingham, MA | 5.57 | 161,000 |
| Los Angeles-Long Beach-Glendale, CA | 5.50 | 3,974,890 |
| Santa Ana-Anaheim-Irvine, CA | 5.49 | 1,452,430 |
| Houston-Sugar Land-Baytown, TX | 5.47 | 2,757,640 |
| Edison-New Brunswick, NJ | 5.43 | 981,480 |
| Wilmington, DE-MD-NJ | 5.35 | 325,530 |
| Baltimore-Towson, MD | 5.33 | 1,280,700 |
| Lowell-Billerica-Chelmsford, MA-NH | 5.32 | 117,190 |
| San Diego-Carlsbad-San Marcos, CA | 5.30 | 1,290,610 |
| Trenton-Ewing, NJ | 5.29 | 215,960 |
| Atlanta-Sandy Springs-Marietta, GA | 5.25 | 2,308,040 |
| Seattle-Bellevue-Everett, WA | 5.21 | 1,449,770 |
| Dallas-Plano-Irving, TX | 5.21 | 2,149,600 |
| Denver-Aurora-Broomfield, CO | 5.19 | 1,280,960 |
| Ann Arbor, MI | 5.18 | 202,700 |
| Midland, TX | 5.11 | 82,750 |
| Sacramento–Arden-Arcade–Roseville, CA | 5.10 | 837,960 |
| Raleigh-Cary, NC | 5.08 | 533,810 |
| Hartford-West Hartford-East Hartford, CT | 5.08 | 559,460 |
| Nashua, NH-MA | 5.07 | 131,800 |
| Philadelphia, PA | 5.07 | 1,840,120 |
| Austin-Round Rock-San Marcos, TX | 5.05 | 854,930 |
| Vallejo-Fairfield, CA | 5.04 | 122,030 |
| Minneapolis-St. Paul-Bloomington, MN-WI | 5.03 | 1,791,390 |
| Oxnard-Thousand Oaks-Ventura, CA | 5.02 | 292,930 |
| Santa Barbara-Santa Maria-Goleta, CA | 5.01 | 172,640 |
| Charlotte-Gastonia-Rock Hill, NC-SC | 5.00 | 877,070 |
| Corvallis, OR | 5.00 | 33,080 |
| Chicago-Joliet-Naperville, IL | 4.99 | 3,700,620 |
| Portsmouth, NH-ME | 4.99 | 56,470 |
| Santa Cruz-Watsonville, CA | 4.95 | 85,420 |
| Camden, NJ | 4.95 | 501,330 |
| Detroit-Livonia-Dearborn, MI | 4.94 | 700,000 |
| Champaign-Urbana, IL | 4.91 | 96,350 |
| Warren-Troy-Farmington Hills, MI | 4.91 | 1,112,130 |
| Lake County-Kenosha County, IL-WI | 4.91 | 379,540 |
| Atlantic City-Hammonton, NJ | 4.84 | 132,980 |
| Poughkeepsie-Newburgh-Middletown, NY | 4.82 | 244,500 |
| Kennewick-Pasco-Richland, WA | 4.82 | 98,520 |
| Providence-Fall River-Warwick, RI-MA | 4.80 | 541,730 |
| Rochester, MN | 4.80 | 103,960 |
| Palm Bay-Melbourne-Titusville, FL | 4.79 | 191,320 |
| Santa Rosa-Petaluma, CA | 4.78 | 176,850 |
| Richmond, VA | 4.78 | 606,070 |
| Colorado Springs, CO | 4.78 | 245,910 |
| Peoria, IL | 4.76 | 180,700 |
| Worcester, MA-CT | 4.75 | 245,320 |
| Fort Collins-Loveland, CO | 4.74 | 136,810 |
| Danbury, CT | 4.72 | 68,940 |
| Bakersfield-Delano, CA | 4.72 | 288,490 |
| Napa, CA | 4.71 | 65,690 |
| New Haven, CT | 4.71 | 272,530 |
| Columbus, OH | 4.70 | 940,940 |
| Columbus, IN | 4.70 | 47,050 |
| Kansas City, MO-KS | 4.69 | 986,500 |
| Norwich-New London, CT-RI | 4.69 | 127,400 |
| Phoenix-Mesa-Glendale, AZ | 4.68 | 1,781,210 |
| St. Louis, MO-IL | 4.67 | 1,291,420 |
| Milwaukee-Waukesha-West Allis, WI | 4.66 | 814,120 |
| Charlottesville, VA | 4.65 | 98,400 |
| Dayton, OH | 4.64 | 368,960 |
| Honolulu, HI | 4.64 | 441,250 |
| Albany-Schenectady-Troy, NY | 4.62 | 427,180 |
| Portland-Vancouver-Hillsboro, OR-WA | 4.62 | 1,027,440 |
| San Luis Obispo-Paso Robles, CA | 4.62 | 102,340 |
| Springfield, IL | 4.62 | 103,640 |
| Riverside-San Bernardino-Ontario, CA | 4.62 | 1,201,500 |
| Bloomington-Normal, IL | 4.61 | 87,020 |
| Fort Worth-Arlington, TX | 4.60 | 911,620 |
| Cincinnati-Middletown, OH-KY-IN | 4.59 | 995,170 |
| Manchester, NH | 4.58 | 101,090 |
| Taunton-Norton-Raynham, MA | 4.58 | 42,580 |
| Salt Lake City, UT | 4.57 | 644,980 |
| Syracuse, NY | 4.57 | 301,060 |
| Rochester-Dover, NH-ME | 4.57 | 53,730 |
| Anchorage, AK | 4.57 | 175,540 |
| Lawrence-Methuen-Salem, MA-NH | 4.56 | 61,100 |
| Madison, WI | 4.56 | 342,930 |
| Madera-Chowchilla, CA | 4.56 | 38,920 |
| Vineland-Millville-Bridgeton, NJ | 4.56 | 58,350 |
| Virginia Beach-Norfolk-Newport News, VA-NC | 4.56 | 724,560 |
| Salinas, CA | 4.54 | 155,210 |
| Ames, IA | 4.54 | 41,460 |
| Indianapolis-Carmel, IN | 4.53 | 912,810 |
| Warner Robins, GA | 4.52 | 56,700 |
| College Station-Bryan, TX | 4.52 | 95,910 |
| Kokomo, IN | 4.51 | 40,260 |
| Iowa City, IA | 4.51 | 88,520 |
| Peabody, MA | 4.51 | 101,600 |
| Hanford-Corcoran, CA | 4.50 | 37,510 |
| Pittsfield, MA | 4.50 | 33,420 |
| Modesto, CA | 4.49 | 157,800 |
| Brockton-Bridgewater-Easton, MA | 4.48 | 89,820 |
| Albuquerque, NM | 4.48 | 368,830 |
| Miami-Miami Beach-Kendall, FL | 4.48 | 1,023,360 |
| Ithaca, NY | 4.46 | 49,070 |
| Gainesville, FL | 4.46 | 120,230 |
| Pittsburgh, PA | 4.46 | 1,130,750 |
| Cleveland-Elyria-Mentor, OH | 4.46 | 1,010,190 |
| Crestview-Fort Walton Beach-Destin, FL | 4.46 | 74,730 |
| Des Moines-West Des Moines, IA | 4.45 | 330,500 |
| Fayetteville-Springdale-Rogers, AR-MO | 4.45 | 208,010 |
| Birmingham-Hoover, AL | 4.44 | 490,870 |
| Charleston-North Charleston-Summerville, SC | 4.44 | 295,210 |
| El Centro, CA | 4.43 | 51,990 |
| Gary, IN | 4.43 | 267,430 |
| Binghamton, NY | 4.43 | 103,490 |
| Rochester, NY | 4.43 | 493,990 |
| Cedar Rapids, IA | 4.43 | 138,580 |
| Fort Lauderdale-Pompano Beach-Deerfield Beach, FL | 4.42 | 732,460 |
| San Antonio-New Braunfels, TX | 4.42 | 887,670 |
| West Palm Beach-Boca Raton-Boynton Beach, FL | 4.42 | 525,170 |
| Buffalo-Niagara Falls, NY | 4.39 | 532,880 |
| Harrisburg-Carlisle, PA | 4.37 | 307,350 |
| Waterbury, CT | 4.37 | 63,440 |
| Chico, CA | 4.37 | 68,410 |
| Springfield, MA-CT | 4.37 | 289,710 |
| State College, PA | 4.36 | 65,710 |
| Beaumont-Port Arthur, TX | 4.36 | 155,790 |
| Winston-Salem, NC | 4.36 | 205,340 |
| Las Cruces, NM | 4.36 | 68,080 |
| Barnstable Town, MA | 4.35 | 97,080 |
| Stockton, CA | 4.35 | 202,710 |
| Oklahoma City, OK | 4.34 | 597,370 |
| New Orleans-Metairie-Kenner, LA | 4.34 | 524,950 |
| New Bedford, MA | 4.34 | 64,030 |
| Augusta-Richmond County, GA-SC | 4.33 | 202,750 |
| Knoxville, TN | 4.32 | 323,770 |
| Lansing-East Lansing, MI | 4.32 | 198,330 |
| Bremerton-Silverdale, WA | 4.32 | 77,850 |
| Savannah, GA | 4.32 | 152,050 |
| Tucson, AZ | 4.32 | 351,610 |
| Allentown-Bethlehem-Easton, PA-NJ | 4.31 | 336,560 |
| Provo-Orem, UT | 4.30 | 187,680 |
| Yuba City, CA | 4.30 | 37,190 |
| Carson City, NV | 4.30 | 25,770 |
| Saginaw-Saginaw Township North, MI | 4.29 | 82,160 |
| Reno-Sparks, NV | 4.29 | 191,930 |
| Omaha-Council Bluffs, NE-IA | 4.29 | 457,580 |
| Haverhill-North Andover-Amesbury, MA-NH | 4.29 | 79,610 |
| Akron, OH | 4.28 | 317,190 |
| Morgantown, WV | 4.28 | 63,050 |
| Las Vegas-Paradise, NV | 4.27 | 839,650 |
| Baton Rouge, LA | 4.27 | 366,610 |
| Tampa-St. Petersburg-Clearwater, FL | 4.27 | 1,151,890 |
| Nashville-Davidson–Murfreesboro–Franklin, TN | 4.27 | 791,190 |
| Fresno, CA | 4.26 | 321,810 |
| Wichita, KS | 4.26 | 284,210 |
| Boise City-Nampa, ID | 4.26 | 269,680 |
| Pascagoula, MS | 4.26 | 53,620 |
| Brunswick, GA | 4.25 | 38,860 |
| Monroe, MI | 4.25 | 38,410 |
| Redding, CA | 4.25 | 56,890 |
| Wilmington, NC | 4.25 | 139,070 |
| Hagerstown-Martinsburg, MD-WV | 4.24 | 101,170 |
| Little Rock-North Little Rock-Conway, AR | 4.24 | 334,770 |
| Montgomery, AL | 4.24 | 159,110 |
| Jacksonville, FL | 4.23 | 586,900 |
| Greenville-Mauldin-Easley, SC | 4.23 | 302,970 |
| Fayetteville, NC | 4.22 | 125,760 |
| Leominster-Fitchburg-Gardner, MA | 4.22 | 46,860 |
| Winchester, VA-WV | 4.22 | 53,370 |
| Tulsa, OK | 4.22 | 421,760 |
| Chattanooga, TN-GA | 4.22 | 227,330 |
| Elmira, NY | 4.21 | 35,790 |
| Kalamazoo-Portage, MI | 4.21 | 129,140 |
| Columbia, MO | 4.21 | 88,930 |
| Memphis, TN-MS-AR | 4.21 | 590,140 |
| Portland-South Portland-Biddeford, ME | 4.20 | 197,620 |
| Blacksburg-Christiansburg-Radford, VA | 4.20 | 63,270 |
| Ogden-Clearfield, UT | 4.20 | 202,960 |
| Decatur, AL | 4.19 | 53,000 |
| Fairbanks, AK | 4.19 | 35,710 |
| Greensboro-High Point, NC | 4.19 | 344,640 |
| Louisville-Jefferson County, KY-IN | 4.18 | 609,210 |
| Flint, MI | 4.17 | 132,000 |
| Columbia, SC | 4.17 | 346,140 |
| Victoria, TX | 4.17 | 51,080 |
| Tallahassee, FL | 4.17 | 156,530 |
| Bay City, MI | 4.17 | 33,490 |
| Battle Creek, MI | 4.17 | 53,370 |
| Burlington-South Burlington, VT | 4.16 | 116,840 |
| Merced, CA | 4.16 | 60,970 |
| Grand Rapids-Wyoming, MI | 4.16 | 397,380 |
| Corpus Christi, TX | 4.15 | 184,760 |
| Kingston, NY | 4.15 | 56,490 |
| Greenville, NC | 4.15 | 75,570 |
| Odessa, TX | 4.14 | 70,850 |
| Lexington-Fayette, KY | 4.14 | 250,070 |
| Jackson, MS | 4.14 | 248,430 |
| Houma-Bayou Cane-Thibodaux, LA | 4.14 | 96,890 |
| Macon, GA | 4.14 | 93,970 |
| Tuscaloosa, AL | 4.14 | 91,640 |
| Manhattan, KS | 4.13 | 50,010 |
| Niles-Benton Harbor, MI | 4.13 | 56,890 |
| Dover, DE | 4.13 | 60,330 |
| Ocean City, NJ | 4.13 | 37,460 |
| Salisbury, MD | 4.13 | 50,780 |
| Columbus, GA-AL | 4.12 | 111,860 |
| Jackson, MI | 4.12 | 55,980 |
| Tyler, TX | 4.11 | 93,020 |
| St. Cloud, MN | 4.11 | 96,930 |
| Duluth, MN-WI | 4.11 | 123,540 |
| Cheyenne, WY | 4.10 | 44,370 |
| Farmington, NM | 4.10 | 50,530 |
| Tacoma, WA | 4.10 | 261,560 |
| Yuma, AZ | 4.09 | 58,880 |
| York-Hanover, PA | 4.09 | 173,250 |
| Parkersburg-Marietta-Vienna, WV-OH | 4.09 | 67,000 |
| Mobile, AL | 4.09 | 167,890 |
| Orlando-Kissimmee-Sanford, FL | 4.08 | 1,042,150 |
| Appleton, WI | 4.08 | 115,480 |
| Waco, TX | 4.08 | 102,810 |
| Reading, PA | 4.08 | 165,800 |
| Roanoke, VA | 4.07 | 149,740 |
| Utica-Rome, NY | 4.07 | 121,790 |
| Amarillo, TX | 4.07 | 110,660 |
| Eau Claire, WI | 4.06 | 78,840 |
| Lafayette, IN | 4.06 | 86,960 |
| Toledo, OH | 4.06 | 297,490 |
| Davenport-Moline-Rock Island, IA-IL | 4.06 | 180,170 |
| Cumberland, MD-WV | 4.05 | 36,630 |
| Elizabethtown, KY | 4.05 | 46,760 |
| Rockford, IL | 4.05 | 143,210 |
| Albany, GA | 4.05 | 58,240 |
| Lincoln, NE | 4.04 | 166,120 |
| Athens-Clarke County, GA | 4.04 | 77,820 |
| Bloomington, IN | 4.04 | 72,550 |
| Billings, MT | 4.04 | 82,610 |
| Rome, GA | 4.03 | 34,730 |
| Lawrence, KS | 4.03 | 45,310 |
| Muncie, IN | 4.03 | 44,540 |
| Laredo, TX | 4.03 | 92,270 |
| Johnstown, PA | 4.03 | 55,560 |
| Auburn-Opelika, AL | 4.03 | 51,010 |
| Holland-Grand Haven, MI | 4.03 | 105,430 |
| Olympia, WA | 4.02 | 95,850 |
| Charleston, WV | 4.02 | 144,200 |
| Mankato-North Mankato, MN | 4.02 | 48,220 |
| Grand Junction, CO | 4.02 | 57,930 |
| Killeen-Temple-Fort Hood, TX | 4.01 | 130,110 |
| Topeka, KS | 4.01 | 108,500 |
| El Paso, TX | 4.01 | 281,570 |
| Sherman-Denison, TX | 4.01 | 41,320 |
| Flagstaff, AZ | 4.00 | 56,200 |
| Janesville, WI | 4.00 | 60,980 |
| Williamsport, PA | 4.00 | 53,550 |
| Greeley, CO | 3.99 | 86,640 |
| South Bend-Mishawaka, IN-MI | 3.99 | 124,570 |
| Racine, WI | 3.99 | 74,250 |
| Huntington-Ashland, WV-KY-OH | 3.99 | 107,810 |
| Decatur, IL | 3.99 | 49,080 |
| Evansville, IN-KY | 3.98 | 169,830 |
| Wausau, WI | 3.98 | 65,330 |
| Fond du Lac, WI | 3.97 | 45,010 |
| Fort Wayne, IN | 3.97 | 202,440 |
| Spartanburg, SC | 3.97 | 121,550 |
| Prescott, AZ | 3.97 | 54,030 |
| Green Bay, WI | 3.96 | 164,630 |
| Sheboygan, WI | 3.96 | 55,490 |
| Gainesville, GA | 3.95 | 73,980 |
| Pueblo, CO | 3.95 | 55,440 |
| Lafayette, LA | 3.94 | 154,340 |
| Naples-Marco Island, FL | 3.94 | 118,850 |
| Erie, PA | 3.94 | 125,060 |
| Missoula, MT | 3.93 | 55,620 |
| Bowling Green, KY | 3.93 | 59,180 |
| Kankakee-Bradley, IL | 3.93 | 40,980 |
| Visalia-Porterville, CA | 3.92 | 133,100 |
| Bangor, ME | 3.92 | 63,290 |
| Hinesville-Fort Stewart, GA | 3.92 | 16,590 |
| Terre Haute, IN | 3.91 | 66,520 |
| Florence, SC | 3.91 | 80,930 |
| Steubenville-Weirton, OH-WV | 3.91 | 40,030 |
| San Angelo, TX | 3.91 | 45,590 |
| Oshkosh-Neenah, WI | 3.91 | 91,970 |
| Salem, OR | 3.90 | 142,940 |
| Shreveport-Bossier City, LA | 3.90 | 172,230 |
| Glens Falls, NY | 3.90 | 52,520 |
| Springfield, MO | 3.90 | 189,080 |
| Canton-Massillon, OH | 3.90 | 165,610 |
| Lake Charles, LA | 3.90 | 88,440 |
| Eugene-Springfield, OR | 3.89 | 139,050 |
| Gulfport-Biloxi, MS | 3.89 | 100,370 |
| Lancaster, PA | 3.89 | 221,960 |
| Casper, WY | 3.88 | 42,080 |
| Bellingham, WA | 3.87 | 76,650 |
| Pocatello, ID | 3.87 | 33,670 |
| Lynchburg, VA | 3.87 | 98,060 |
| Bend, OR | 3.87 | 62,540 |
| Longview, WA | 3.86 | 33,810 |
| Pensacola-Ferry Pass-Brent, FL | 3.86 | 153,140 |
| Lubbock, TX | 3.86 | 129,310 |
| Grand Forks, ND-MN | 3.86 | 50,400 |
| Muskegon-Norton Shores, MI | 3.86 | 57,300 |
| Fargo, ND-MN | 3.86 | 128,990 |
| Lima, OH | 3.85 | 48,890 |
| Longview, TX | 3.85 | 98,900 |
| Danville, IL | 3.85 | 26,960 |
| Scranton–Wilkes-Barre, PA | 3.84 | 250,300 |
| North Port-Bradenton-Sarasota, FL | 3.84 | 246,570 |
| Mount Vernon-Anacortes, WA | 3.83 | 43,140 |
| Clarksville, TN-KY | 3.83 | 82,080 |
| Abilene, TX | 3.83 | 62,610 |
| Lawton, OK | 3.82 | 40,990 |
| Johnson City, TN | 3.82 | 76,790 |
| La Crosse, WI-MN | 3.81 | 73,490 |
| Kingsport-Bristol-Bristol, TN-VA | 3.81 | 114,400 |
| Springfield, OH | 3.81 | 46,890 |
| Michigan City-La Porte, IN | 3.81 | 40,560 |
| Port St. Lucie, FL | 3.80 | 124,990 |
| Lake Havasu City-Kingman, AZ | 3.80 | 44,070 |
| Rocky Mount, NC | 3.79 | 54,900 |
| Alexandria, LA | 3.79 | 60,470 |
| Spokane, WA | 3.78 | 200,200 |
| Youngstown-Warren-Boardman, OH-PA | 3.78 | 218,770 |
| Cape Coral-Fort Myers, FL | 3.78 | 211,080 |
| Valdosta, GA | 3.77 | 49,620 |
| Medford, OR | 3.77 | 76,410 |
| Wenatchee-East Wenatchee, WA | 3.77 | 39,110 |
| Coeur d'Alene, ID | 3.76 | 53,450 |
| Panama City-Lynn Haven-Panama City Beach, FL | 3.76 | 70,530 |
| Lebanon, PA | 3.76 | 50,150 |
| Bismarck, ND | 3.76 | 68,060 |
| St. Joseph, MO-KS | 3.75 | 52,170 |
| McAllen-Edinburg-Mission, TX | 3.75 | 233,640 |
| Cleveland, TN | 3.72 | 38,950 |
| Asheville, NC | 3.71 | 171,890 |
| Idaho Falls, ID | 3.71 | 50,150 |
| Burlington, NC | 3.71 | 55,910 |
| Jacksonville, NC | 3.71 | 44,250 |
| Waterloo-Cedar Falls, IA | 3.71 | 89,450 |
| Pine Bluff, AR | 3.70 | 33,170 |
| Altoona, PA | 3.69 | 57,730 |
| Dubuque, IA | 3.67 | 56,990 |
| Santa Fe, NM | 3.67 | 59,140 |
| Sumter, SC | 3.67 | 33,690 |
| Anderson, IN | 3.66 | 37,820 |
| Sandusky, OH | 3.66 | 35,490 |
| Sioux Falls, SD | 3.66 | 141,470 |
| Jefferson City, MO | 3.66 | 72,060 |
| Punta Gorda, FL | 3.66 | 40,900 |
| Cape Girardeau-Jackson, MO-IL | 3.65 | 42,060 |
| Florence-Muscle Shoals, AL | 3.65 | 51,990 |
| Dothan, AL | 3.65 | 55,180 |
| Mansfield, OH | 3.64 | 48,890 |
| Sebastian-Vero Beach, FL | 3.64 | 46,100 |
| Lakeland-Winter Haven, FL | 3.63 | 196,400 |
| Logan, UT-ID | 3.63 | 49,880 |
| Great Falls, MT | 3.62 | 34,490 |
| Wheeling, WV-OH | 3.62 | 62,850 |
| Lewiston-Auburn, ME | 3.61 | 46,730 |
| Brownsville-Harlingen, TX | 3.61 | 131,270 |
| Wichita Falls, TX | 3.60 | 56,010 |
| Hot Springs, AR | 3.59 | 34,530 |
| Dalton, GA | 3.59 | 61,920 |
| Hattiesburg, MS | 3.58 | 56,500 |
| Owensboro, KY | 3.58 | 49,410 |
| Harrisonburg, VA | 3.57 | 58,680 |
| Ocala, FL | 3.56 | 90,860 |
| Jackson, TN | 3.56 | 57,830 |
| Lewiston, ID-WA | 3.56 | 24,050 |
| Joplin, MO | 3.56 | 77,900 |
| Gadsden, AL | 3.54 | 34,490 |
| Elkhart-Goshen, IN | 3.54 | 114,420 |
| Rapid City, SD | 3.54 | 60,640 |
| Monroe, LA | 3.54 | 74,190 |
| Anderson, SC | 3.53 | 60,100 |
| Texarkana-Texarkana, TX-AR | 3.53 | 52,980 |
| Yakima, WA | 3.52 | 80,460 |
| Fort Smith, AR-OK | 3.52 | 112,020 |
| Goldsboro, NC | 3.51 | 39,060 |
| Deltona-Daytona Beach-Ormond Beach, FL | 3.51 | 152,950 |
| Anniston-Oxford, AL | 3.51 | 43,150 |
| Sioux City, IA-NE-SD | 3.51 | 71,070 |
| St. George, UT | 3.49 | 49,730 |
| Danville, VA | 3.46 | 37,000 |
| Jonesboro, AR | 3.42 | 50,350 |
| Hickory-Lenoir-Morganton, NC | 3.41 | 143,700 |
| Myrtle Beach-North Myrtle Beach-Conway, SC | 3.39 | 112,720 |
| Palm Coast, FL | 3.34 | 18,950 |
| Morristown, TN | 3.28 | 43,970 |
Table 1 shows the U.S. Census regions, the number of metropolitan areas in those regions, and the range of 90–10 ratios found there. More than 20 percent of the metropolitan statistical areas in the Northeast region and its regional divisions had above-average 90–10 wage ratios in 2013. In addition, the lowest
| Region | Number of MSAs | Average 90–10 ratio | Highest 90–10 ratio | Lowest 90–10 ratio | Number of MSAs above average | Percent of MSAs above average |
|---|---|---|---|---|---|---|
| Northeast | 63 | 4.56 | 6.28 | 3.61 | 14 | 22.2 |
| New England | 29 | 4.65 | 6.00 | 3.61 | 7 | 24.1 |
| Middle Atlantic | 34 | 4.49 | 6.28 | 3.69 | 7 | 20.6 |
| Midwest | 96 | 4.16 | 5.18 | 3.51 | 7 | 7.3 |
| East North Central | 64 | 4.20 | 5.18 | 3.54 | 6 | 9.4 |
| West North Central | 32 | 4.08 | 5.03 | 3.51 | 1 | 3.1 |
| South | 153 | 4.13 | 6.77 | 3.28 | 13 | 8.5 |
| South Atlantic | 80 | 4.18 | 6.77 | 3.35 | 8 | 10.0 |
| East South Central | 30 | 4.01 | 6.16 | 3.28 | 1 | 3.3 |
| West South Central | 43 | 4.11 | 5.47 | 3.42 | 4 | 9.3 |
| West | 83 | 4.40 | 7.14 | 3.49 | 15 | 18.1 |
| Mountain | 35 | 4.16 | 5.68 | 3.49 | 2 | 5.7 |
| Pacific | 48 | 4.58 | 7.14 | 3.53 | 13 | 27.1 |
| Note: The New England Division includes Connecticut, Maine, Massachusetts, New Hampshire, Rhode Island, and Vermont. The Middle Atlantic Division includes New Jersey, New York, and Pennsylvania. The East North Central Division includes Illinois, Indiana, Michigan, Ohio, and Wisconsin. The West North Central Division includes Iowa, Kansas, Minnesota, Missouri, Nebraska, North Dakota, and South Dakota. The South Atlantic Division includes Delaware, District of Columbia, Florida, Georgia, Maryland, North Carolina, South Carolina, Virginia, and West Virginia. The East South Central Division includes Alabama, Kentucky, Mississippi, and Tennessee. The West South Central Division includes Arkansas, Louisiana, Oklahoma, and Texas. The Mountain Division includes Arizona, Colorado, Idaho, Montana, Nevada, New Mexico, Utah, and Wyoming. The Pacific Division includes Alaska, California, Hawaii, Oregon, and Washington. Source: U.S. Bureau of Labor Statistics. | ||||||
In addition to being concentrated in the Northeast and on the West Coast, metropolitan areas with the highest 90–10 ratios tend to be the larger areas, including the Washington, New York, San Francisco, and Oakland metropolitan areas, although there are some exceptions. Figure 3 shows a simple scatter plot of the 90–10 ratio relative to the size of the area as measured by employment for all occupations in that area. The upward-sloping trend line indicates that larger areas tend to have higher 90–10 ratios.
| Metropolitan statistical area | Employment | 90–10 ratio |
|---|---|---|
| San Jose-Sunnyvale-Santa Clara, CA | 930,070 | 7.14 |
| Washington-Arlington-Alexandria, DC-VA-MD-WV | 2,367,240 | 6.76 |
| Bethesda-Rockville-Frederick, MD | 561,830 | 6.29 |
| New York-White Plains-Wayne, NY-NJ | 5,242,070 | 6.28 |
| Huntsville, AL | 210,110 | 6.16 |
| San Francisco-San Mateo-Redwood City, CA | 1,045,700 | 6.15 |
| Oakland-Fremont-Hayward, CA | 1,003,860 | 6.03 |
| Bridgeport-Stamford-Norwalk, CT | 420,170 | 6.00 |
| Durham-Chapel Hill, NC | 276,580 | 5.76 |
| Boulder, CO | 163,010 | 5.68 |
| Boston-Cambridge-Quincy, MA | 1,748,940 | 5.63 |
| Nassau-Suffolk, NY | 1,235,610 | 5.62 |
| Newark-Union, NJ-PA | 957,630 | 5.58 |
| Framingham, MA | 161,000 | 5.57 |
| Los Angeles-Long Beach-Glendale, CA | 3,974,890 | 5.50 |
| Santa Ana-Anaheim-Irvine, CA | 1,452,430 | 5.49 |
| Houston-Sugar Land-Baytown, TX | 2,757,640 | 5.47 |
| Edison-New Brunswick, NJ | 981,480 | 5.43 |
| Wilmington, DE-MD-NJ | 325,530 | 5.35 |
| Baltimore-Towson, MD | 1,280,700 | 5.33 |
| Lowell-Billerica-Chelmsford, MA-NH | 117,190 | 5.32 |
| San Diego-Carlsbad-San Marcos, CA | 1,290,610 | 5.30 |
| Trenton-Ewing, NJ | 215,960 | 5.29 |
| Atlanta-Sandy Springs-Marietta, GA | 2,308,040 | 5.25 |
| Seattle-Bellevue-Everett, WA | 1,449,770 | 5.21 |
| Dallas-Plano-Irving, TX | 2,149,600 | 5.21 |
| Denver-Aurora-Broomfield, CO | 1,280,960 | 5.19 |
| Ann Arbor, MI | 202,700 | 5.18 |
| Midland, TX | 82,750 | 5.11 |
| Sacramento–Arden-Arcade–Roseville, CA | 837,960 | 5.10 |
| Raleigh-Cary, NC | 533,810 | 5.08 |
| Hartford-West Hartford-East Hartford, CT | 559,460 | 5.08 |
| Nashua, NH-MA | 131,800 | 5.07 |
| Philadelphia, PA | 1,840,120 | 5.07 |
| Austin-Round Rock-San Marcos, TX | 854,930 | 5.05 |
| Vallejo-Fairfield, CA | 122,030 | 5.04 |
| Minneapolis-St. Paul-Bloomington, MN-WI | 1,791,390 | 5.03 |
| Oxnard-Thousand Oaks-Ventura, CA | 292,930 | 5.02 |
| Santa Barbara-Santa Maria-Goleta, CA | 172,640 | 5.01 |
| Charlotte-Gastonia-Rock Hill, NC-SC | 877,070 | 5.00 |
| Corvallis, OR | 33,080 | 5.00 |
| Chicago-Joliet-Naperville, IL | 3,700,620 | 4.99 |
| Portsmouth, NH-ME | 56,470 | 4.99 |
| Santa Cruz-Watsonville, CA | 85,420 | 4.95 |
| Camden, NJ | 501,330 | 4.95 |
| Detroit-Livonia-Dearborn, MI | 700,000 | 4.94 |
| Champaign-Urbana, IL | 96,350 | 4.91 |
| Warren-Troy-Farmington Hills, MI | 1,112,130 | 4.91 |
| Lake County-Kenosha County, IL-WI | 379,540 | 4.91 |
| Atlantic City-Hammonton, NJ | 132,980 | 4.84 |
| Poughkeepsie-Newburgh-Middletown, NY | 244,500 | 4.82 |
| Kennewick-Pasco-Richland, WA | 98,520 | 4.82 |
| Providence-Fall River-Warwick, RI-MA | 541,730 | 4.80 |
| Rochester, MN | 103,960 | 4.80 |
| Palm Bay-Melbourne-Titusville, FL | 191,320 | 4.79 |
| Santa Rosa-Petaluma, CA | 176,850 | 4.78 |
| Richmond, VA | 606,070 | 4.78 |
| Colorado Springs, CO | 245,910 | 4.78 |
| Peoria, IL | 180,700 | 4.76 |
| Worcester, MA-CT | 245,320 | 4.75 |
| Fort Collins-Loveland, CO | 136,810 | 4.74 |
| Danbury, CT | 68,940 | 4.72 |
| Bakersfield-Delano, CA | 288,490 | 4.72 |
| Napa, CA | 65,690 | 4.71 |
| New Haven, CT | 272,530 | 4.71 |
| Columbus, OH | 940,940 | 4.70 |
| Columbus, IN | 47,050 | 4.70 |
| Kansas City, MO-KS | 986,500 | 4.69 |
| Norwich-New London, CT-RI | 127,400 | 4.69 |
| Phoenix-Mesa-Glendale, AZ | 1,781,210 | 4.68 |
| St. Louis, MO-IL | 1,291,420 | 4.67 |
| Milwaukee-Waukesha-West Allis, WI | 814,120 | 4.66 |
| Charlottesville, VA | 98,400 | 4.65 |
| Dayton, OH | 368,960 | 4.64 |
| Honolulu, HI | 441,250 | 4.64 |
| Albany-Schenectady-Troy, NY | 427,180 | 4.62 |
| Portland-Vancouver-Hillsboro, OR-WA | 1,027,440 | 4.62 |
| San Luis Obispo-Paso Robles, CA | 102,340 | 4.62 |
| Springfield, IL | 103,640 | 4.62 |
| Riverside-San Bernardino-Ontario, CA | 1,201,500 | 4.62 |
| Bloomington-Normal, IL | 87,020 | 4.61 |
| Fort Worth-Arlington, TX | 911,620 | 4.60 |
| Cincinnati-Middletown, OH-KY-IN | 995,170 | 4.59 |
| Manchester, NH | 101,090 | 4.58 |
| Taunton-Norton-Raynham, MA | 42,580 | 4.58 |
| Salt Lake City, UT | 644,980 | 4.57 |
| Syracuse, NY | 301,060 | 4.57 |
| Rochester-Dover, NH-ME | 53,730 | 4.57 |
| Anchorage, AK | 175,540 | 4.57 |
| Lawrence-Methuen-Salem, MA-NH | 61,100 | 4.56 |
| Madison, WI | 342,930 | 4.56 |
| Madera-Chowchilla, CA | 38,920 | 4.56 |
| Vineland-Millville-Bridgeton, NJ | 58,350 | 4.56 |
| Virginia Beach-Norfolk-Newport News, VA-NC | 724,560 | 4.56 |
| Salinas, CA | 155,210 | 4.54 |
| Ames, IA | 41,460 | 4.54 |
| Indianapolis-Carmel, IN | 912,810 | 4.53 |
| Warner Robins, GA | 56,700 | 4.52 |
| College Station-Bryan, TX | 95,910 | 4.52 |
| Kokomo, IN | 40,260 | 4.51 |
| Iowa City, IA | 88,520 | 4.51 |
| Peabody, MA | 101,600 | 4.51 |
| Hanford-Corcoran, CA | 37,510 | 4.50 |
| Pittsfield, MA | 33,420 | 4.50 |
| Modesto, CA | 157,800 | 4.49 |
| Brockton-Bridgewater-Easton, MA | 89,820 | 4.48 |
| Albuquerque, NM | 368,830 | 4.48 |
| Miami-Miami Beach-Kendall, FL | 1,023,360 | 4.48 |
| Ithaca, NY | 49,070 | 4.46 |
| Gainesville, FL | 120,230 | 4.46 |
| Pittsburgh, PA | 1,130,750 | 4.46 |
| Cleveland-Elyria-Mentor, OH | 1,010,190 | 4.46 |
| Crestview-Fort Walton Beach-Destin, FL | 74,730 | 4.46 |
| Des Moines-West Des Moines, IA | 330,500 | 4.45 |
| Fayetteville-Springdale-Rogers, AR-MO | 208,010 | 4.45 |
| Birmingham-Hoover, AL | 490,870 | 4.44 |
| Charleston-North Charleston-Summerville, SC | 295,210 | 4.44 |
| El Centro, CA | 51,990 | 4.43 |
| Gary, IN | 267,430 | 4.43 |
| Binghamton, NY | 103,490 | 4.43 |
| Rochester, NY | 493,990 | 4.43 |
| Cedar Rapids, IA | 138,580 | 4.43 |
| Fort Lauderdale-Pompano Beach-Deerfield Beach, FL | 732,460 | 4.42 |
| San Antonio-New Braunfels, TX | 887,670 | 4.42 |
| West Palm Beach-Boca Raton-Boynton Beach, FL | 525,170 | 4.42 |
| Buffalo-Niagara Falls, NY | 532,880 | 4.39 |
| Harrisburg-Carlisle, PA | 307,350 | 4.37 |
| Waterbury, CT | 63,440 | 4.37 |
| Chico, CA | 68,410 | 4.37 |
| Springfield, MA-CT | 289,710 | 4.37 |
| State College, PA | 65,710 | 4.36 |
| Beaumont-Port Arthur, TX | 155,790 | 4.36 |
| Winston-Salem, NC | 205,340 | 4.36 |
| Las Cruces, NM | 68,080 | 4.36 |
| Barnstable Town, MA | 97,080 | 4.35 |
| Stockton, CA | 202,710 | 4.35 |
| Oklahoma City, OK | 597,370 | 4.34 |
| New Orleans-Metairie-Kenner, LA | 524,950 | 4.34 |
| New Bedford, MA | 64,030 | 4.34 |
| Augusta-Richmond County, GA-SC | 202,750 | 4.33 |
| Knoxville, TN | 323,770 | 4.32 |
| Lansing-East Lansing, MI | 198,330 | 4.32 |
| Bremerton-Silverdale, WA | 77,850 | 4.32 |
| Savannah, GA | 152,050 | 4.32 |
| Tucson, AZ | 351,610 | 4.32 |
| Allentown-Bethlehem-Easton, PA-NJ | 336,560 | 4.31 |
| Provo-Orem, UT | 187,680 | 4.30 |
| Yuba City, CA | 37,190 | 4.30 |
| Carson City, NV | 25,770 | 4.30 |
| Saginaw-Saginaw Township North, MI | 82,160 | 4.29 |
| Reno-Sparks, NV | 191,930 | 4.29 |
| Omaha-Council Bluffs, NE-IA | 457,580 | 4.29 |
| Haverhill-North Andover-Amesbury, MA-NH | 79,610 | 4.29 |
| Akron, OH | 317,190 | 4.28 |
| Morgantown, WV | 63,050 | 4.28 |
| Las Vegas-Paradise, NV | 839,650 | 4.27 |
| Baton Rouge, LA | 366,610 | 4.27 |
| Tampa-St. Petersburg-Clearwater, FL | 1,151,890 | 4.27 |
| Nashville-Davidson–Murfreesboro–Franklin, TN | 791,190 | 4.27 |
| Fresno, CA | 321,810 | 4.26 |
| Wichita, KS | 284,210 | 4.26 |
| Boise City-Nampa, ID | 269,680 | 4.26 |
| Pascagoula, MS | 53,620 | 4.26 |
| Brunswick, GA | 38,860 | 4.25 |
| Monroe, MI | 38,410 | 4.25 |
| Redding, CA | 56,890 | 4.25 |
| Wilmington, NC | 139,070 | 4.25 |
| Hagerstown-Martinsburg, MD-WV | 101,170 | 4.24 |
| Little Rock-North Little Rock-Conway, AR | 334,770 | 4.24 |
| Montgomery, AL | 159,110 | 4.24 |
| Jacksonville, FL | 586,900 | 4.23 |
| Greenville-Mauldin-Easley, SC | 302,970 | 4.23 |
| Fayetteville, NC | 125,760 | 4.22 |
| Leominster-Fitchburg-Gardner, MA | 46,860 | 4.22 |
| Winchester, VA-WV | 53,370 | 4.22 |
| Tulsa, OK | 421,760 | 4.22 |
| Chattanooga, TN-GA | 227,330 | 4.22 |
| Elmira, NY | 35,790 | 4.21 |
| Kalamazoo-Portage, MI | 129,140 | 4.21 |
| Columbia, MO | 88,930 | 4.21 |
| Memphis, TN-MS-AR | 590,140 | 4.21 |
| Portland-South Portland-Biddeford, ME | 197,620 | 4.20 |
| Blacksburg-Christiansburg-Radford, VA | 63,270 | 4.20 |
| Ogden-Clearfield, UT | 202,960 | 4.20 |
| Decatur, AL | 53,000 | 4.19 |
| Fairbanks, AK | 35,710 | 4.19 |
| Greensboro-High Point, NC | 344,640 | 4.19 |
| Louisville-Jefferson County, KY-IN | 609,210 | 4.18 |
| Flint, MI | 132,000 | 4.17 |
| Columbia, SC | 346,140 | 4.17 |
| Victoria, TX | 51,080 | 4.17 |
| Tallahassee, FL | 156,530 | 4.17 |
| Bay City, MI | 33,490 | 4.17 |
| Battle Creek, MI | 53,370 | 4.17 |
| Burlington-South Burlington, VT | 116,840 | 4.16 |
| Merced, CA | 60,970 | 4.16 |
| Grand Rapids-Wyoming, MI | 397,380 | 4.16 |
| Corpus Christi, TX | 184,760 | 4.15 |
| Kingston, NY | 56,490 | 4.15 |
| Greenville, NC | 75,570 | 4.15 |
| Odessa, TX | 70,850 | 4.14 |
| Lexington-Fayette, KY | 250,070 | 4.14 |
| Jackson, MS | 248,430 | 4.14 |
| Houma-Bayou Cane-Thibodaux, LA | 96,890 | 4.14 |
| Macon, GA | 93,970 | 4.14 |
| Tuscaloosa, AL | 91,640 | 4.14 |
| Manhattan, KS | 50,010 | 4.13 |
| Niles-Benton Harbor, MI | 56,890 | 4.13 |
| Dover, DE | 60,330 | 4.13 |
| Ocean City, NJ | 37,460 | 4.13 |
| Salisbury, MD | 50,780 | 4.13 |
| Columbus, GA-AL | 111,860 | 4.12 |
| Jackson, MI | 55,980 | 4.12 |
| Tyler, TX | 93,020 | 4.11 |
| St. Cloud, MN | 96,930 | 4.11 |
| Duluth, MN-WI | 123,540 | 4.11 |
| Cheyenne, WY | 44,370 | 4.10 |
| Farmington, NM | 50,530 | 4.10 |
| Tacoma, WA | 261,560 | 4.10 |
| Yuma, AZ | 58,880 | 4.09 |
| York-Hanover, PA | 173,250 | 4.09 |
| Parkersburg-Marietta-Vienna, WV-OH | 67,000 | 4.09 |
| Mobile, AL | 167,890 | 4.09 |
| Orlando-Kissimmee-Sanford, FL | 1,042,150 | 4.08 |
| Appleton, WI | 115,480 | 4.08 |
| Waco, TX | 102,810 | 4.08 |
| Reading, PA | 165,800 | 4.08 |
| Roanoke, VA | 149,740 | 4.07 |
| Utica-Rome, NY | 121,790 | 4.07 |
| Amarillo, TX | 110,660 | 4.07 |
| Eau Claire, WI | 78,840 | 4.06 |
| Lafayette, IN | 86,960 | 4.06 |
| Toledo, OH | 297,490 | 4.06 |
| Davenport-Moline-Rock Island, IA-IL | 180,170 | 4.06 |
| Cumberland, MD-WV | 36,630 | 4.05 |
| Elizabethtown, KY | 46,760 | 4.05 |
| Rockford, IL | 143,210 | 4.05 |
| Albany, GA | 58,240 | 4.05 |
| Lincoln, NE | 166,120 | 4.04 |
| Athens-Clarke County, GA | 77,820 | 4.04 |
| Bloomington, IN | 72,550 | 4.04 |
| Billings, MT | 82,610 | 4.04 |
| Rome, GA | 34,730 | 4.03 |
| Lawrence, KS | 45,310 | 4.03 |
| Muncie, IN | 44,540 | 4.03 |
| Laredo, TX | 92,270 | 4.03 |
| Johnstown, PA | 55,560 | 4.03 |
| Auburn-Opelika, AL | 51,010 | 4.03 |
| Holland-Grand Haven, MI | 105,430 | 4.03 |
| Olympia, WA | 95,850 | 4.02 |
| Charleston, WV | 144,200 | 4.02 |
| Mankato-North Mankato, MN | 48,220 | 4.02 |
| Grand Junction, CO | 57,930 | 4.02 |
| Killeen-Temple-Fort Hood, TX | 130,110 | 4.01 |
| Topeka, KS | 108,500 | 4.01 |
| El Paso, TX | 281,570 | 4.01 |
| Sherman-Denison, TX | 41,320 | 4.01 |
| Flagstaff, AZ | 56,200 | 4.00 |
| Janesville, WI | 60,980 | 4.00 |
| Williamsport, PA | 53,550 | 4.00 |
| Greeley, CO | 86,640 | 3.99 |
| South Bend-Mishawaka, IN-MI | 124,570 | 3.99 |
| Racine, WI | 74,250 | 3.99 |
| Huntington-Ashland, WV-KY-OH | 107,810 | 3.99 |
| Decatur, IL | 49,080 | 3.99 |
| Evansville, IN-KY | 169,830 | 3.98 |
| Wausau, WI | 65,330 | 3.98 |
| Fond du Lac, WI | 45,010 | 3.97 |
| Fort Wayne, IN | 202,440 | 3.97 |
| Spartanburg, SC | 121,550 | 3.97 |
| Prescott, AZ | 54,030 | 3.97 |
| Green Bay, WI | 164,630 | 3.96 |
| Sheboygan, WI | 55,490 | 3.96 |
| Gainesville, GA | 73,980 | 3.95 |
| Pueblo, CO | 55,440 | 3.95 |
| Lafayette, LA | 154,340 | 3.94 |
| Naples-Marco Island, FL | 118,850 | 3.94 |
| Erie, PA | 125,060 | 3.94 |
| Missoula, MT | 55,620 | 3.93 |
| Bowling Green, KY | 59,180 | 3.93 |
| Kankakee-Bradley, IL | 40,980 | 3.93 |
| Visalia-Porterville, CA | 133,100 | 3.92 |
| Bangor, ME | 63,290 | 3.92 |
| Hinesville-Fort Stewart, GA | 16,590 | 3.92 |
| Terre Haute, IN | 66,520 | 3.91 |
| Florence, SC | 80,930 | 3.91 |
| Steubenville-Weirton, OH-WV | 40,030 | 3.91 |
| San Angelo, TX | 45,590 | 3.91 |
| Oshkosh-Neenah, WI | 91,970 | 3.91 |
| Salem, OR | 142,940 | 3.90 |
| Shreveport-Bossier City, LA | 172,230 | 3.90 |
| Glens Falls, NY | 52,520 | 3.90 |
| Springfield, MO | 189,080 | 3.90 |
| Canton-Massillon, OH | 165,610 | 3.90 |
| Lake Charles, LA | 88,440 | 3.90 |
| Eugene-Springfield, OR | 139,050 | 3.89 |
| Gulfport-Biloxi, MS | 100,370 | 3.89 |
| Lancaster, PA | 221,960 | 3.89 |
| Casper, WY | 42,080 | 3.88 |
| Bellingham, WA | 76,650 | 3.87 |
| Pocatello, ID | 33,670 | 3.87 |
| Lynchburg, VA | 98,060 | 3.87 |
| Bend, OR | 62,540 | 3.87 |
| Longview, WA | 33,810 | 3.86 |
| Pensacola-Ferry Pass-Brent, FL | 153,140 | 3.86 |
| Lubbock, TX | 129,310 | 3.86 |
| Grand Forks, ND-MN | 50,400 | 3.86 |
| Muskegon-Norton Shores, MI | 57,300 | 3.86 |
| Fargo, ND-MN | 128,990 | 3.86 |
| Lima, OH | 48,890 | 3.85 |
| Longview, TX | 98,900 | 3.85 |
| Danville, IL | 26,960 | 3.85 |
| Scranton–Wilkes-Barre, PA | 250,300 | 3.84 |
| North Port-Bradenton-Sarasota, FL | 246,570 | 3.84 |
| Mount Vernon-Anacortes, WA | 43,140 | 3.83 |
| Clarksville, TN-KY | 82,080 | 3.83 |
| Abilene, TX | 62,610 | 3.83 |
| Lawton, OK | 40,990 | 3.82 |
| Johnson City, TN | 76,790 | 3.82 |
| La Crosse, WI-MN | 73,490 | 3.81 |
| Kingsport-Bristol-Bristol, TN-VA | 114,400 | 3.81 |
| Springfield, OH | 46,890 | 3.81 |
| Michigan City-La Porte, IN | 40,560 | 3.81 |
| Port St. Lucie, FL | 124,990 | 3.80 |
| Lake Havasu City-Kingman, AZ | 44,070 | 3.80 |
| Rocky Mount, NC | 54,900 | 3.79 |
| Alexandria, LA | 60,470 | 3.79 |
| Spokane, WA | 200,200 | 3.78 |
| Youngstown-Warren-Boardman, OH-PA | 218,770 | 3.78 |
| Cape Coral-Fort Myers, FL | 211,080 | 3.78 |
| Valdosta, GA | 49,620 | 3.77 |
| Medford, OR | 76,410 | 3.77 |
| Wenatchee-East Wenatchee, WA | 39,110 | 3.77 |
| Coeur d'Alene, ID | 53,450 | 3.76 |
| Panama City-Lynn Haven-Panama City Beach, FL | 70,530 | 3.76 |
| Lebanon, PA | 50,150 | 3.76 |
| Bismarck, ND | 68,060 | 3.76 |
| St. Joseph, MO-KS | 52,170 | 3.75 |
| McAllen-Edinburg-Mission, TX | 233,640 | 3.75 |
| Cleveland, TN | 38,950 | 3.72 |
| Asheville, NC | 171,890 | 3.71 |
| Idaho Falls, ID | 50,150 | 3.71 |
| Burlington, NC | 55,910 | 3.71 |
| Jacksonville, NC | 44,250 | 3.71 |
| Waterloo-Cedar Falls, IA | 89,450 | 3.71 |
| Pine Bluff, AR | 33,170 | 3.70 |
| Altoona, PA | 57,730 | 3.69 |
| Dubuque, IA | 56,990 | 3.67 |
| Santa Fe, NM | 59,140 | 3.67 |
| Sumter, SC | 33,690 | 3.67 |
| Anderson, IN | 37,820 | 3.66 |
| Sandusky, OH | 35,490 | 3.66 |
| Sioux Falls, SD | 141,470 | 3.66 |
| Jefferson City, MO | 72,060 | 3.66 |
| Punta Gorda, FL | 40,900 | 3.66 |
| Cape Girardeau-Jackson, MO-IL | 42,060 | 3.65 |
| Florence-Muscle Shoals, AL | 51,990 | 3.65 |
| Dothan, AL | 55,180 | 3.65 |
| Mansfield, OH | 48,890 | 3.64 |
| Sebastian-Vero Beach, FL | 46,100 | 3.64 |
| Lakeland-Winter Haven, FL | 196,400 | 3.63 |
| Logan, UT-ID | 49,880 | 3.63 |
| Great Falls, MT | 34,490 | 3.62 |
| Wheeling, WV-OH | 62,850 | 3.62 |
| Lewiston-Auburn, ME | 46,730 | 3.61 |
| Brownsville-Harlingen, TX | 131,270 | 3.61 |
| Wichita Falls, TX | 56,010 | 3.60 |
| Hot Springs, AR | 34,530 | 3.59 |
| Dalton, GA | 61,920 | 3.59 |
| Hattiesburg, MS | 56,500 | 3.58 |
| Owensboro, KY | 49,410 | 3.58 |
| Harrisonburg, VA | 58,680 | 3.57 |
| Ocala, FL | 90,860 | 3.56 |
| Jackson, TN | 57,830 | 3.56 |
| Lewiston, ID-WA | 24,050 | 3.56 |
| Joplin, MO | 77,900 | 3.56 |
| Gadsden, AL | 34,490 | 3.54 |
| Elkhart-Goshen, IN | 114,420 | 3.54 |
| Rapid City, SD | 60,640 | 3.54 |
| Monroe, LA | 74,190 | 3.54 |
| Anderson, SC | 60,100 | 3.53 |
| Texarkana-Texarkana, TX-AR | 52,980 | 3.53 |
| Yakima, WA | 80,460 | 3.52 |
| Fort Smith, AR-OK | 112,020 | 3.52 |
| Goldsboro, NC | 39,060 | 3.51 |
| Deltona-Daytona Beach-Ormond Beach, FL | 152,950 | 3.51 |
| Anniston-Oxford, AL | 43,150 | 3.51 |
| Sioux City, IA-NE-SD | 71,070 | 3.51 |
| St. George, UT | 49,730 | 3.49 |
| Danville, VA | 37,000 | 3.46 |
| Jonesboro, AR | 50,350 | 3.42 |
| Hickory-Lenoir-Morganton, NC | 143,700 | 3.41 |
| Myrtle Beach-North Myrtle Beach-Conway, SC | 112,720 | 3.39 |
| Palm Coast, FL | 18,950 | 3.34 |
| Morristown, TN | 43,970 | 3.28 |
Table 2 shows the share of metropolitan statistical areas with above-average ratios, by size. As the size categories get smaller, so does the percentage of areas with above-average 90–10 ratios. But table 2 also shows that there are several exceptions. In the largest size category, for example, roughly one-third of the areas have below-average 90–10 ratios. At the same time, in the smallest size category (employment of less than 100,000), there were five areas with above-average 90–10 ratios.
| Total employment | Number of MSAs | Number of MSAs with 90–10 ratio above 4.86 | Percent of MSAs with 90–10 ratio above 4.86 |
|---|---|---|---|
| 1,000,000 or more | 28 | 19 | 67.9 |
| 500,000 to 999,999 | 32 | 11 | 34.4 |
| 100,000 to 499,999 | 144 | 14 | 9.7 |
| Less than 100,000 | 191 | 5 | 2.6 |
| Source: U.S. Bureau of Labor Statistics. | |||
The five small MSAs with 90–10 ratios above 4.86 and the nine large MSAs with 90–10 ratios below 4.86 are shown in table 3. Aside from being small, the five MSAs with above-average 90–10 ratios have little else in common. All are located in separate states and at least several hundred miles apart. Santa Cruz-Watsonville is close to other areas with high 90–10 ratios, such as San Jose-Sunnyvale-Santa Clara, San Francisco, and Oakland; but Midland, TX, is several hundred miles away from the nearest area with an above-average 90–10 ratio. The closest large metropolitan area to Corvallis, OR, is Portland-Vancouver-Hillsboro, but it is one of the large areas with below-average inequality.
Figure 4 helps isolate the patterns in inequality across MSA sizes, which can be caused by differences in either the 90th-percentile wages or the 10th-percentile wages. As can be seen in figure 4, the 10th-percentile wage varies little across the size groups while the 90th-percentile wage varies considerably, with higher wages for the larger areas and lower wages for the smaller ones. Thus, the main reason for the higher 90–10 ratios in the larger areas is that the 90th-percentile wage is higher in those areas. In other words, the highest paid workers in the large areas generally earn more than the highest paid workers in the smaller areas, whereas the wages of the lowest paid workers vary less between large and small areas.
| Employment | 90th-percentile wage | 10th-percentile wage |
|---|---|---|
| Total, United States | $42.47 | $8.74 |
| 1,000,000 or more | 47.06 | 9.07 |
| 500,000 to 999,999 | 42.23 | 8.76 |
| 100,000 to 499,999 | 37.44 | 8.67 |
| Less than 100,000 | 34.41 | 8.57 |
| Source: U.S. Bureau of Labor Statistics. | ||
Table 3 shows the exceptions to what is shown in figure 4. Although Midland, TX, is small, and its 10th-percentile wage ($8.69) is close to average for its size, its 90th-percentile wage is $44.44, which is higher than the 90th-percentile wage nationally and higher than the 90th-percentile wage for the second largest MSA size category. Portland-Vancouver-Hillsboro, part of the largest MSA category, has a 90th-percentile wage of $44.08, about $3 below the average for that size category, and its 10th-percentile wage is $9.54, considerably higher than the average among the largest MSAs.
| Metropolitian Statistical Area | Total employment | 90–10 ratio |
|---|---|---|
| Midland, TX | 82,750 | 5.11 |
| Corvallis, OR | 33,080 | 5.00 |
| Portsmouth, NH-ME | 56,470 | 4.99 |
| Santa Cruz-Watsonville, CA | 85,420 | 4.95 |
| Champaign-Urbana, IL | 96,350 | 4.91 |
| Phoenix-Mesa-Glendale, AZ | 1,781,210 | 4.68 |
| St. Louis, MO-IL | 1,291,420 | 4.67 |
| Portland-Vancouver-Hillsboro, OR-WA | 1,027,440 | 4.62 |
| Riverside-San Bernardino-Ontario, CA | 1,201,500 | 4.62 |
| Miami-Miami Beach-Kendall, FL | 1,023,360 | 4.48 |
| Pittsburgh, PA | 1,130,750 | 4.46 |
| Cleveland-Elyria-Mentor, OH | 1,010,190 | 4.46 |
| Tampa-St. Petersburg-Clearwater, FL | 1,151,890 | 4.27 |
| Orlando-Kissimmee-Sanford, FL | 1,042,150 | 4.08 |
| Source: U.S. Bureau of Labor Statistics. | ||
Figures 5 and 6 show how the 90–10 ratios for a subset of metropolitan areas changed over the 2003–13 period.1 Figure 5 shows the percent change in the ratio itself, while figure 6 shows the percent change in the 90th- and 10th-percentile wage values. As can be seen in figure 5, the 90–10 ratio increased for all MSA size categories over the period, but it increased much more in the larger areas (those with employment of 1 million or more).
| MSA employment | Percent change |
|---|---|
| Total, U.S. average | 7.0 |
| 1,000,000 or more | 10.3 |
| 500,000 to 999,999 | 3.2 |
| 100,000 to 499,999 | 2.4 |
| Less than 100,000 | 2.4 |
Figure 6 shows that for each size category, the 90th-percentile wage grew faster than the 10th-percentile wage. The figure also shows that the 90th-percentile wages in the smaller areas grew faster than those in the two middle size categories, but the 10th-percentile wages also grew faster in the smaller areas, which helps explain why the 90–10 ratios grew more slowly in the smaller areas than in the larger areas.
| MSA employment | Percent change, 90th percentile | Percent change, 10th percentile |
|---|---|---|
| Total, U.S. average | 32.8 | 24.1 |
| 1,000,000 or more | 35.6 | 22.7 |
| 500,000 to 999,999 | 28.9 | 24.8 |
| 100,000 to 499,999 | 28.4 | 25.2 |
| Less than 100,000 | 31.0 | 27.6 |
| Source: U.S. Bureau of Labor Statistics. | ||
The occupational composition of a particular metropolitan area can influence its 90–10 ratio. Generally speaking, greater-than-average shares of employment in either very high-paying or very low-paying occupations can increase the ratio. In fact, areas with high concentrations of high-paying occupations, such as computer and mathematical occupations, tend to have greater wage inequality (as measured by their 90–10 ratios). Table 4 shows the 22 major occupational groups and their 90th-percentile wages in May 2013. The table shows that 8 of the 22 occupation groups have 90th-percentile wages above the 90th-percentile wage for all occupations: management, business and financial operations, computer and mathematical, architecture and engineering; life, physical, and social science; legal; arts, design, entertainment, sports, and media; and healthcare practitioners and technical. Areas with high percentages of these occupations often have relatively high 90–10 ratios.
| Major occupational group | Employment | Percent of total employment | 90th-percentile wage |
|---|---|---|---|
| All occupations | 132,588,810 | 100.0 | $88,330 |
| Management occupations | 6,542,950 | 4.9 | 187,199 |
| Business and financial operations occupations | 6,658,090 | 5.0 | 113,650 |
| Computer and mathematical occupations | 3,696,180 | 2.8 | 130,600 |
| Architecture and engineering occupations | 2,380,840 | 1.8 | 126,250 |
| Life, physical, and social science occupations | 1,135,030 | 0.9 | 116,280 |
| Community and social service occupations | 1,901,730 | 1.4 | 72,290 |
| Legal occupations | 1,041,700 | 0.8 | 187,199 |
| Education, training, and library occupations | 8,400,640 | 6.3 | 87,000 |
| Arts, design, entertainment, sports, and media occupations | 1,758,310 | 1.3 | 98,660 |
| Healthcare practitioners and technical occupations | 7,755,810 | 5.8 | 131,530 |
| Healthcare support occupations | 3,924,390 | 3.0 | 41,640 |
| Protective service occupations | 3,257,690 | 2.5 | 79,100 |
| Food preparation and serving related occupations | 11,914,590 | 9.0 | 30,640 |
| Building and grounds cleaning and maintenance occupations | 4,291,410 | 3.2 | 39,980 |
| Personal care and service occupations | 3,986,740 | 3.0 | 38,040 |
| Sales and related occupations | 14,068,190 | 10.6 | 74,430 |
| Office and administrative support occupations | 21,442,800 | 16.2 | 55,200 |
| Farming, fishing, and forestry occupations | 435,250 | 0.3 | 39,040 |
| Construction and extraction occupations | 5,088,030 | 3.8 | 74,920 |
| Installation, maintenance, and repair occupations | 5,138,130 | 3.9 | 71,090 |
| Production occupations | 8,765,180 | 6.6 | 57,080 |
| Transportation and material moving occupations | 9,005,120 | 6.8 | 56,320 |
| Source: U.S. Bureau of Labor Statistics. | |||
Figure 7 illustrates this relationship for computer and mathematical occupations. Each dot in the figure represents a particular metropolitan statistical area, with the 90–10 ratio for all occupations on the x-axis and the percentage employment in computer and mathematical occupations on the y-axis. As can be seen, there is a positive relationship between computer and mathematical occupations employment and the
| Metropolitan Statistical Area | Percent | 90–10 ratio |
|---|---|---|
| San Jose-Sunnyvale-Santa Clara, CA | 10.5 | 7.14 |
| Washington-Arlington-Alexandria, DC-VA-MD-WV | 8.0 | 6.76 |
| Bethesda-Rockville-Frederick, MD | 5.9 | 6.29 |
| New York-White Plains-Wayne, NY-NJ | 3.1 | 6.28 |
| Huntsville, AL | 6.5 | 6.16 |
| San Francisco-San Mateo-Redwood City, CA | 6.6 | 6.15 |
| Oakland-Fremont-Hayward, CA | 4.0 | 6.03 |
| Bridgeport-Stamford-Norwalk, CT | 3.3 | 6.00 |
| Durham-Chapel Hill, NC | 6.4 | 5.76 |
| Boulder, CO | 6.7 | 5.68 |
| Boston-Cambridge-Quincy, MA | 5.5 | 5.63 |
| Nassau-Suffolk, NY | 1.8 | 5.62 |
| Newark-Union, NJ-PA | 2.9 | 5.58 |
| Framingham, MA | 8.4 | 5.57 |
| Los Angeles-Long Beach-Glendale, CA | 2.4 | 5.50 |
| Santa Ana-Anaheim-Irvine, CA | 3.3 | 5.49 |
| Houston-Sugar Land-Baytown, TX | 2.7 | 5.47 |
| Edison-New Brunswick, NJ | 4.3 | 5.43 |
| Wilmington, DE-MD-NJ | 3.6 | 5.35 |
| Baltimore-Towson, MD | 4.3 | 5.33 |
| Lowell-Billerica-Chelmsford, MA-NH | 5.0 | 5.32 |
| San Diego-Carlsbad-San Marcos, CA | 3.5 | 5.30 |
| Trenton-Ewing, NJ | 5.1 | 5.29 |
| Atlanta-Sandy Springs-Marietta, GA | 4.0 | 5.25 |
| Seattle-Bellevue-Everett, WA | 8.0 | 5.21 |
| Dallas-Plano-Irving, TX | 4.7 | 5.21 |
| Denver-Aurora-Broomfield, CO | 4.6 | 5.19 |
| Ann Arbor, MI | 3.8 | 5.18 |
| Midland, TX | 1.2 | 5.11 |
| Sacramento–Arden-Arcade–Roseville, CA | 3.6 | 5.10 |
| Raleigh-Cary, NC | 5.3 | 5.08 |
| Hartford-West Hartford-East Hartford, CT | 3.6 | 5.08 |
| Nashua, NH-MA | 3.9 | 5.07 |
| Philadelphia, PA | 3.4 | 5.07 |
| Austin-Round Rock-San Marcos, TX | 5.9 | 5.05 |
| Vallejo-Fairfield, CA | 1.3 | 5.04 |
| Minneapolis-St. Paul-Bloomington, MN-WI | 3.9 | 5.03 |
| Oxnard-Thousand Oaks-Ventura, CA | 2.4 | 5.02 |
| Santa Barbara-Santa Maria-Goleta, CA | 2.5 | 5.01 |
| Charlotte-Gastonia-Rock Hill, NC-SC | 3.5 | 5.00 |
| Corvallis, OR | 4.5 | 5.00 |
| Chicago-Joliet-Naperville, IL | 3.2 | 4.99 |
| Portsmouth, NH-ME | 4.4 | 4.99 |
| Santa Cruz-Watsonville, CA | 2.0 | 4.95 |
| Camden, NJ | 2.0 | 4.95 |
| Detroit-Livonia-Dearborn, MI | 3.0 | 4.94 |
| Champaign-Urbana, IL | 2.5 | 4.91 |
| Warren-Troy-Farmington Hills, MI | 3.4 | 4.91 |
| Lake County-Kenosha County, IL-WI | 3.2 | 4.91 |
| Atlantic City-Hammonton, NJ | 1.7 | 4.84 |
| Poughkeepsie-Newburgh-Middletown, NY | 1.9 | 4.82 |
| Kennewick-Pasco-Richland, WA | 1.9 | 4.82 |
| Providence-Fall River-Warwick, RI-MA | 2.5 | 4.80 |
| Rochester, MN | 5.1 | 4.80 |
| Palm Bay-Melbourne-Titusville, FL | 4.2 | 4.79 |
| Santa Rosa-Petaluma, CA | 1.6 | 4.78 |
| Richmond, VA | 3.4 | 4.78 |
| Colorado Springs, CO | 5.1 | 4.78 |
| Peoria, IL | 2.5 | 4.76 |
| Worcester, MA-CT | 2.6 | 4.75 |
| Danbury, CT | 1.7 | 4.72 |
| Bakersfield-Delano, CA | 1.6 | 4.72 |
| Napa, CA | 0.7 | 4.71 |
| New Haven, CT | 1.8 | 4.71 |
| Columbus, OH | 4.3 | 4.70 |
| Columbus, IN | 2.2 | 4.70 |
| Kansas City, MO-KS | 3.7 | 4.69 |
| Norwich-New London, CT-RI | 1.8 | 4.69 |
| Phoenix-Mesa-Glendale, AZ | 3.4 | 4.68 |
| St. Louis, MO-IL | 3.3 | 4.67 |
| Milwaukee-Waukesha-West Allis, WI | 2.8 | 4.66 |
| Charlottesville, VA | 3.4 | 4.65 |
| Dayton, OH | 3.2 | 4.64 |
| Honolulu, HI | 1.9 | 4.64 |
| Albany-Schedy-Troy, NY | 3.4 | 4.62 |
| Portland-Vancouver-Hillsboro, OR-WA | 3.4 | 4.62 |
| San Luis Obispo-Paso Robles, CA | 1.6 | 4.62 |
| Springfield, IL | 2.3 | 4.62 |
| Riverside-San Bernardino-Ontario, CA | 1.1 | 4.62 |
| Bloomington-Normal, IL | 6.0 | 4.61 |
| Fort Worth-Arlington, TX | 2.4 | 4.60 |
| Cincinnati-Middletown, OH-KY-IN | 2.9 | 4.59 |
| Manchester, NH | 3.0 | 4.58 |
| Taunton-Norton-Raynham, MA | 2.1 | 4.58 |
| Salt Lake City, UT | 3.3 | 4.57 |
| Syracuse, NY | 1.9 | 4.57 |
| Rochester-Dover, NH-ME | 3.9 | 4.57 |
| Anchorage, AK | 1.9 | 4.57 |
| Lawrence-Methuen-Salem, MA-NH | 1.7 | 4.56 |
| Madison, WI | 5.0 | 4.56 |
| Madera-Chowchilla, CA | 0.8 | 4.56 |
| Vineland-Millville-Bridgeton, NJ | 0.6 | 4.56 |
| Virginia Beach-Norfolk-Newport News, VA-NC | 3.0 | 4.56 |
| Salinas, CA | 1.4 | 4.54 |
| Ames, IA | 3.3 | 4.54 |
| Indianapolis-Carmel, IN | 3.0 | 4.53 |
| Warner Robins, GA | 2.6 | 4.52 |
| College Station-Bryan, TX | 2.0 | 4.52 |
| Iowa City, IA | 2.5 | 4.51 |
| Peabody, MA | 1.1 | 4.51 |
| Hanford-Corcoran, CA | 0.5 | 4.50 |
| Pittsfield, MA | 2.5 | 4.50 |
| Modesto, CA | 1.0 | 4.49 |
| Brockton-Bridgewater-Easton, MA | 0.9 | 4.48 |
| Albuquerque, NM | 2.4 | 4.48 |
| Miami-Miami Beach-Kendall, FL | 1.6 | 4.48 |
| Ithaca, NY | 2.0 | 4.46 |
| Gainesville, FL | 2.3 | 4.46 |
| Pittsburgh, PA | 2.8 | 4.46 |
| Cleveland-Elyria-Mentor, OH | 2.8 | 4.46 |
| Crestview-Fort Walton Beach-Destin, FL | 3.2 | 4.46 |
| Des Moines-West Des Moines, IA | 3.7 | 4.45 |
| Fayetteville-Springdale-Rogers, AR-MO | 3.2 | 4.45 |
| Birmingham-Hoover, AL | 2.7 | 4.44 |
| Charleston-North Charleston-Summerville, SC | 2.5 | 4.44 |
| El Centro, CA | 0.7 | 4.43 |
| Gary, IN | 0.8 | 4.43 |
| Binghamton, NY | 1.8 | 4.43 |
| Rochester, NY | 3.0 | 4.43 |
| Cedar Rapids, IA | 3.9 | 4.43 |
| Fort Lauderdale-Pompano Beach-Deerfield Beach, FL | 2.2 | 4.42 |
| San Antonio-New Braunfels, TX | 2.7 | 4.42 |
| West Palm Beach-Boca Raton-Boynton Beach, FL | 2.2 | 4.42 |
| Buffalo-Niagara Falls, NY | 2.4 | 4.39 |
| Harrisburg-Carlisle, PA | 3.6 | 4.37 |
| Waterbury, CT | 0.9 | 4.37 |
| Chico, CA | 1.3 | 4.37 |
| Springfield, MA-CT | 1.6 | 4.37 |
| State College, PA | 3.4 | 4.36 |
| Beaumont-Port Arthur, TX | 0.9 | 4.36 |
| Winston-Salem, NC | 2.0 | 4.36 |
| Las Cruces, NM | 2.0 | 4.36 |
| Barnstable Town, MA | 1.1 | 4.35 |
| Stockton, CA | 0.9 | 4.35 |
| Oklahoma City, OK | 2.3 | 4.34 |
| New Orleans-Metairie-Kenner, LA | 1.2 | 4.34 |
| New Bedford, MA | 0.6 | 4.34 |
| Augusta-Richmond County, GA-SC | 1.6 | 4.33 |
| Knoxville, TN | 1.9 | 4.32 |
| Lansing-East Lansing, MI | 3.4 | 4.32 |
| Bremerton-Silverdale, WA | 1.9 | 4.32 |
| Savannah, GA | 1.0 | 4.32 |
| Tucson, AZ | 2.9 | 4.32 |
| Allentown-Bethlehem-Easton, PA-NJ | 2.0 | 4.31 |
| Provo-Orem, UT | 4.3 | 4.30 |
| Yuba City, CA | 0.8 | 4.30 |
| Carson City, NV | 2.3 | 4.30 |
| Saginaw-Saginaw Township North, MI | 1.2 | 4.29 |
| Reno-Sparks, NV | 1.7 | 4.29 |
| Omaha-Council Bluffs, NE-IA | 3.9 | 4.29 |
| Haverhill-North Andover-Amesbury, MA-NH | 1.4 | 4.29 |
| Akron, OH | 2.7 | 4.28 |
| Morgantown, WV | 2.7 | 4.28 |
| Las Vegas-Paradise, NV | 1.3 | 4.27 |
| Baton Rouge, LA | 1.5 | 4.27 |
| Tampa-St. Petersburg-Clearwater, FL | 3.0 | 4.27 |
| Nashville-Davidson–Murfreesboro–Franklin, TN | 2.5 | 4.27 |
| Fresno, CA | 0.9 | 4.26 |
| Wichita, KS | 2.1 | 4.26 |
| Boise City-Nampa, ID | 2.8 | 4.26 |
| Pascagoula, MS | 2.0 | 4.26 |
| Brunswick, GA | 0.7 | 4.25 |
| Monroe, MI | 0.7 | 4.25 |
| Redding, CA | 1.0 | 4.25 |
| Wilmington, NC | 1.6 | 4.25 |
| Hagerstown-Martinsburg, MD-WV | 2.8 | 4.24 |
| Little Rock-North Little Rock-Conway, AR | 2.9 | 4.24 |
| Montgomery, AL | 2.6 | 4.24 |
| Jacksonville, FL | 2.8 | 4.23 |
| Greenville-Mauldin-Easley, SC | 2.2 | 4.23 |
| Fayetteville, NC | 1.6 | 4.22 |
| Leominster-Fitchburg-Gardner, MA | 1.3 | 4.22 |
| Winchester, VA-WV | 1.1 | 4.22 |
| Tulsa, OK | 1.6 | 4.22 |
| Chattanooga, TN-GA | 1.4 | 4.22 |
| Elmira, NY | 0.7 | 4.21 |
| Kalamazoo-Portage, MI | 1.8 | 4.21 |
| Columbia, MO | 2.5 | 4.21 |
| Memphis, TN-MS-AR | 1.6 | 4.21 |
| Portland-South Portland-Biddeford, ME | 2.6 | 4.20 |
| Blacksburg-Christiansburg-Radford, VA | 1.7 | 4.20 |
| Ogden-Clearfield, UT | 2.2 | 4.20 |
| Decatur, AL | 0.7 | 4.19 |
| Fairbanks, AK | 1.8 | 4.19 |
| Greensboro-High Point, NC | 1.9 | 4.19 |
| Louisville-Jefferson County, KY-IN | 2.1 | 4.18 |
| Flint, MI | 1.5 | 4.17 |
| Columbia, SC | 2.6 | 4.17 |
| Victoria, TX | 0.6 | 4.17 |
| Tallahassee, FL | 3.6 | 4.17 |
| Bay City, MI | 0.5 | 4.17 |
| Battle Creek, MI | 1.5 | 4.17 |
| Burlington-South Burlington, VT | 3.5 | 4.16 |
| Merced, CA | 0.7 | 4.16 |
| Grand Rapids-Wyoming, MI | 2.4 | 4.16 |
| Corpus Christi, TX | 0.9 | 4.15 |
| Kingston, NY | 1.0 | 4.15 |
| Greenville, NC | 1.3 | 4.15 |
| Odessa, TX | 0.9 | 4.14 |
| Lexington-Fayette, KY | 2.3 | 4.14 |
| Jackson, MS | 1.6 | 4.14 |
| Houma-Bayou Cane-Thibodaux, LA | 0.4 | 4.14 |
| Macon, GA | 1.7 | 4.14 |
| Tuscaloosa, AL | 1.1 | 4.14 |
| Manhattan, KS | 1.9 | 4.13 |
| Niles-Benton Harbor, MI | 0.9 | 4.13 |
| Dover, DE | 1.4 | 4.13 |
| Ocean City, NJ | 0.4 | 4.13 |
| Salisbury, MD | 1.2 | 4.13 |
| Columbus, GA-AL | 3.0 | 4.12 |
| Jackson, MI | 1.4 | 4.12 |
| Tyler, TX | 1.6 | 4.11 |
| St. Cloud, MN | 1.6 | 4.11 |
| Duluth, MN-WI | 1.4 | 4.11 |
| Cheyenne, WY | 2.1 | 4.10 |
| Farmington, NM | 0.6 | 4.10 |
| Tacoma, WA | 1.4 | 4.10 |
| Yuma, AZ | 1.7 | 4.09 |
| York-Hanover, PA | 1.3 | 4.09 |
| Parkersburg-Marietta-Vienna, WV-OH | 1.1 | 4.09 |
| Mobile, AL | 1.9 | 4.09 |
| Orlando-Kissimmee-Sanford, FL | 2.5 | 4.08 |
| Appleton, WI | 1.6 | 4.08 |
| Waco, TX | 1.4 | 4.08 |
| Reading, PA | 1.5 | 4.08 |
| Roanoke, VA | 1.6 | 4.07 |
| Utica-Rome, NY | 1.9 | 4.07 |
| Amarillo, TX | 1.4 | 4.07 |
| Eau Claire, WI | 2.1 | 4.06 |
| Lafayette, IN | 1.2 | 4.06 |
| Toledo, OH | 1.3 | 4.06 |
| Davenport-Moline-Rock Island, IA-IL | 2.1 | 4.06 |
| Cumberland, MD-WV | 1.7 | 4.05 |
| Elizabethtown, KY | 2.6 | 4.05 |
| Rockford, IL | 0.9 | 4.05 |
| Albany, GA | 1.1 | 4.05 |
| Lincoln, NE | 3.3 | 4.04 |
| Athens-Clarke County, GA | 1.1 | 4.04 |
| Bloomington, IN | 2.1 | 4.04 |
| Billings, MT | 1.6 | 4.04 |
| Rome, GA | 0.9 | 4.03 |
| Lawrence, KS | 2.1 | 4.03 |
| Muncie, IN | 1.5 | 4.03 |
| Laredo, TX | 0.7 | 4.03 |
| Johnstown, PA | 1.2 | 4.03 |
| Auburn-Opelika, AL | 1.2 | 4.03 |
| Holland-Grand Haven, MI | 1.4 | 4.03 |
| Olympia, WA | 4.9 | 4.02 |
| Charleston, WV | 1.2 | 4.02 |
| Mankato-North Mankato, MN | 1.5 | 4.02 |
| Grand Junction, CO | 0.8 | 4.02 |
| Killeen-Temple-Fort Hood, TX | 2.0 | 4.01 |
| Topeka, KS | 2.5 | 4.01 |
| El Paso, TX | 1.1 | 4.01 |
| Sherman-Denison, TX | 1.5 | 4.01 |
| Flagstaff, AZ | 1.3 | 4.00 |
| Janesville, WI | 1.2 | 4.00 |
| Williamsport, PA | 1.0 | 4.00 |
| Greeley, CO | 1.3 | 3.99 |
| South Bend-Mishawaka, IN-MI | 1.2 | 3.99 |
| Racine, WI | 0.7 | 3.99 |
| Huntington-Ashland, WV-KY-OH | 0.7 | 3.99 |
| Decatur, IL | 0.6 | 3.99 |
| Evansville, IN-KY | 1.2 | 3.98 |
| Wausau, WI | 2.6 | 3.98 |
| Fond du Lac, WI | 1.0 | 3.97 |
| Fort Wayne, IN | 1.8 | 3.97 |
| Spartanburg, SC | 1.4 | 3.97 |
| Prescott, AZ | 0.9 | 3.97 |
| Green Bay, WI | 2.4 | 3.96 |
| Sheboygan, WI | 1.5 | 3.96 |
| Gainesville, GA | 1.0 | 3.95 |
| Pueblo, CO | 0.9 | 3.95 |
| Lafayette, LA | 1.0 | 3.94 |
| Naples-Marco Island, FL | 1.0 | 3.94 |
| Erie, PA | 1.0 | 3.94 |
| Missoula, MT | 1.7 | 3.93 |
| Bowling Green, KY | 1.6 | 3.93 |
| Kankakee-Bradley, IL | 0.6 | 3.93 |
| Visalia-Porterville, CA | 0.6 | 3.92 |
| Bangor, ME | 1.2 | 3.92 |
| Hinesville-Fort Stewart, GA | 1.4 | 3.92 |
| Terre Haute, IN | 0.8 | 3.91 |
| Florence, SC | 1.7 | 3.91 |
| Steubenville-Weirton, OH-WV | 1.7 | 3.91 |
| San Angelo, TX | 1.1 | 3.91 |
| Oshkosh-Neenah, WI | 1.7 | 3.91 |
| Salem, OR | 2.2 | 3.90 |
| Shreveport-Bossier City, LA | 0.7 | 3.90 |
| Glens Falls, NY | 0.7 | 3.90 |
| Springfield, MO | 1.8 | 3.90 |
| Canton-Massillon, OH | 0.9 | 3.90 |
| Lake Charles, LA | 0.4 | 3.90 |
| Eugene-Springfield, OR | 2.1 | 3.89 |
| Gulfport-Biloxi, MS | 1.3 | 3.89 |
| Lancaster, PA | 1.2 | 3.89 |
| Casper, WY | 0.8 | 3.88 |
| Bellingham, WA | 1.7 | 3.87 |
| Pocatello, ID | 0.9 | 3.87 |
| Lynchburg, VA | 1.4 | 3.87 |
| Bend, OR | 1.6 | 3.87 |
| Longview, WA | 0.7 | 3.86 |
| Pensacola-Ferry Pass-Brent, FL | 1.8 | 3.86 |
| Lubbock, TX | 1.3 | 3.86 |
| Grand Forks, ND-MN | 1.0 | 3.86 |
| Muskegon-Norton Shores, MI | 0.7 | 3.86 |
| Fargo, ND-MN | 2.4 | 3.86 |
| Lima, OH | 0.4 | 3.85 |
| Longview, TX | 0.8 | 3.85 |
| Danville, IL | 0.7 | 3.85 |
| Scranton–Wilkes-Barre, PA | 1.3 | 3.84 |
| North Port-Bradenton-Sarasota, FL | 1.4 | 3.84 |
| Mount Vernon-Anacortes, WA | 1.1 | 3.83 |
| Clarksville, TN-KY | 1.0 | 3.83 |
| Abilene, TX | 1.3 | 3.83 |
| Lawton, OK | 1.4 | 3.82 |
| Johnson City, TN | 1.1 | 3.82 |
| La Crosse, WI-MN | 1.3 | 3.81 |
| Kingsport-Bristol-Bristol, TN-VA | 1.2 | 3.81 |
| Springfield, OH | 1.5 | 3.81 |
| Michigan City-La Porte, IN | 0.8 | 3.81 |
| Port St. Lucie, FL | 0.9 | 3.80 |
| Lake Havasu City-Kingman, AZ | 1.0 | 3.80 |
| Rocky Mount, NC | 0.9 | 3.79 |
| Alexandria, LA | 0.7 | 3.79 |
| Spokane, WA | 2.1 | 3.78 |
| Youngstown-Warren-Boardman, OH-PA | 1.0 | 3.78 |
| Cape Coral-Fort Myers, FL | 1.2 | 3.78 |
| Valdosta, GA | 0.8 | 3.77 |
| Medford, OR | 1.6 | 3.77 |
| Wenatchee-East Wenatchee, WA | 1.0 | 3.77 |
| Coeur d'Alene, ID | 1.2 | 3.76 |
| Panama City-Lynn Haven-Panama City Beach, FL | 1.0 | 3.76 |
| Lebanon, PA | 0.7 | 3.76 |
| Bismarck, ND | 2.1 | 3.76 |
| St. Joseph, MO-KS | 0.7 | 3.75 |
| McAllen-Edinburg-Mission, TX | 0.7 | 3.75 |
| Cleveland, TN | 0.9 | 3.72 |
| Asheville, NC | 1.0 | 3.71 |
| Idaho Falls, ID | 1.1 | 3.71 |
| Burlington, NC | 1.1 | 3.71 |
| Jacksonville, NC | 0.9 | 3.71 |
| Waterloo-Cedar Falls, IA | 1.4 | 3.71 |
| Pine Bluff, AR | 1.1 | 3.70 |
| Altoona, PA | 1.1 | 3.69 |
| Dubuque, IA | 3.6 | 3.67 |
| Santa Fe, NM | 2.0 | 3.67 |
| Sumter, SC | 1.2 | 3.67 |
| Anderson, IN | 0.7 | 3.66 |
| Sandusky, OH | 0.8 | 3.66 |
| Sioux Falls, SD | 2.5 | 3.66 |
| Jefferson City, MO | 3.3 | 3.66 |
| Punta Gorda, FL | 0.9 | 3.66 |
| Cape Girardeau-Jackson, MO-IL | 0.9 | 3.65 |
| Florence-Muscle Shoals, AL | 0.5 | 3.65 |
| Dothan, AL | 0.6 | 3.65 |
| Mansfield, OH | 0.9 | 3.64 |
| Sebastian-Vero Beach, FL | 1.0 | 3.64 |
| Lakeland-Winter Haven, FL | 1.4 | 3.63 |
| Logan, UT-ID | 1.9 | 3.63 |
| Great Falls, MT | 1.5 | 3.62 |
| Wheeling, WV-OH | 1.0 | 3.62 |
| Lewiston-Auburn, ME | 1.4 | 3.61 |
| Brownsville-Harlingen, TX | 0.6 | 3.61 |
| Wichita Falls, TX | 0.8 | 3.60 |
| Hot Springs, AR | 0.9 | 3.59 |
| Dalton, GA | 1.9 | 3.59 |
| Hattiesburg, MS | 1.0 | 3.58 |
| Owensboro, KY | 0.7 | 3.58 |
| Harrisonburg, VA | 1.4 | 3.57 |
| Ocala, FL | 0.9 | 3.56 |
| Jackson, TN | 0.7 | 3.56 |
| Lewiston, ID-WA | 1.2 | 3.56 |
| Joplin, MO | 1.0 | 3.56 |
| Gadsden, AL | 0.3 | 3.54 |
| Elkhart-Goshen, IN | 1.0 | 3.54 |
| Rapid City, SD | 1.4 | 3.54 |
| Monroe, LA | 1.0 | 3.54 |
| Anderson, SC | 0.6 | 3.53 |
| Texarkana-Texarkana, TX-AR | 0.7 | 3.53 |
| Yakima, WA | 0.8 | 3.52 |
| Fort Smith, AR-OK | 0.9 | 3.52 |
| Goldsboro, NC | 1.1 | 3.51 |
| Deltona-Daytona Beach-Ormond Beach, FL | 1.1 | 3.51 |
| Anniston-Oxford, AL | 0.8 | 3.51 |
| Sioux City, IA-NE-SD | 1.4 | 3.51 |
| St. George, UT | 0.9 | 3.49 |
| Danville, VA | 0.6 | 3.46 |
| Jonesboro, AR | 0.7 | 3.42 |
| Hickory-Lenoir-Morganton, NC | 0.8 | 3.41 |
| Myrtle Beach-North Myrtle Beach-Conway, SC | 0.7 | 3.39 |
| Palm Coast, FL | 1.2 | 3.34 |
| Morristown, TN | 0.7 | 3.28 |
Table 5 shows the R2 value between employment share and the 90–10 ratio for the eight highest paying major occupation groups. A positive relationship exists for all but one of the occupational groups. Those with relatively high R2 values include management occupations, business and financial operations occupations, and architecture and engineering occupations.
| Major occupational group | R2 value | Slope of trend line |
|---|---|---|
| Management occupations | 0.42 | Positive |
| Business and financial operations occupations | 0.42 | Positive |
| Computer and mathematical occupations | 0.55 | Positive |
| Architecture and engineering occupations | 0.25 | Positive |
| Life, physical, and social science occupations | 0.17 | Positive |
| Legal occupations | 0.17 | Positive |
| Arts, design, entertainment, sports, and media occupations | 0.20 | Positive |
| Healthcare practitioners and technical occupations | 0.05 | Negative |
| Source: U.S. Bureau of Labor Statistics. | ||
The one exception is healthcare practitioners and technical occupations, for which the correlation is weak and the trend line is negative, as can be seen in figure 8. Nationally, the 90th-percentile wage for healthcare practitioner and technical occupations is the third-highest among the 22 major groups, and the average share of total employment is 5.8 percent. Nevertheless, there is a weak negative relationship among MSAs with respect to employment share in these occupations and their 90–10 ratios.
| Metropolitan Statistical Area | Percent | 90–10 ratio |
|---|---|---|
| San Jose-Sunnyvale-Santa Clara, CA | 4.1 | 7.14 |
| Washington-Arlington-Alexandria, DC-VA-MD-WV | 4.1 | 6.76 |
| Bethesda-Rockville-Frederick, MD | 6.7 | 6.29 |
| New York-White Plains-Wayne, NY-NJ | 5.2 | 6.28 |
| Huntsville, AL | 5.4 | 6.16 |
| San Francisco-San Mateo-Redwood City, CA | 3.9 | 6.15 |
| Oakland-Fremont-Hayward, CA | 5.5 | 6.03 |
| Bridgeport-Stamford-Norwalk, CT | 5.5 | 6.00 |
| Durham-Chapel Hill, NC | 9.2 | 5.76 |
| Boulder, CO | 5.0 | 5.68 |
| Boston-Cambridge-Quincy, MA | 7.1 | 5.63 |
| Nassau-Suffolk, NY | 6.4 | 5.62 |
| Newark-Union, NJ-PA | 5.3 | 5.58 |
| Framingham, MA | 4.8 | 5.57 |
| Los Angeles-Long Beach-Glendale, CA | 5.0 | 5.50 |
| Santa Ana-Anaheim-Irvine, CA | 4.5 | 5.49 |
| Houston-Sugar Land-Baytown, TX | 4.9 | 5.47 |
| Edison-New Brunswick, NJ | 5.7 | 5.43 |
| Wilmington, DE-MD-NJ | 6.5 | 5.35 |
| Baltimore-Towson, MD | 6.4 | 5.33 |
| Lowell-Billerica-Chelmsford, MA-NH | 5.6 | 5.32 |
| San Diego-Carlsbad-San Marcos, CA | 5.2 | 5.30 |
| Trenton-Ewing, NJ | 5.9 | 5.29 |
| Atlanta-Sandy Springs-Marietta, GA | 4.9 | 5.25 |
| Seattle-Bellevue-Everett, WA | 4.7 | 5.21 |
| Dallas-Plano-Irving, TX | 5.1 | 5.21 |
| Denver-Aurora-Broomfield, CO | 5.1 | 5.19 |
| Ann Arbor, MI | 10.4 | 5.18 |
| Midland, TX | 3.6 | 5.11 |
| Sacramento–Arden-Arcade–Roseville, CA | 5.4 | 5.10 |
| Raleigh-Cary, NC | 5.0 | 5.08 |
| Hartford-West Hartford-East Hartford, CT | 6.4 | 5.08 |
| Nashua, NH-MA | 4.2 | 5.07 |
| Philadelphia, PA | 6.4 | 5.07 |
| Austin-Round Rock-San Marcos, TX | 4.4 | 5.05 |
| Vallejo-Fairfield, CA | 7.4 | 5.04 |
| Minneapolis-St. Paul-Bloomington, MN-WI | 5.2 | 5.03 |
| Oxnard-Thousand Oaks-Ventura, CA | 4.0 | 5.02 |
| Santa Barbara-Santa Maria-Goleta, CA | 4.6 | 5.01 |
| Charlotte-Gastonia-Rock Hill, NC-SC | 5.5 | 5.00 |
| Corvallis, OR | 6.6 | 5.00 |
| Chicago-Joliet-Naperville, IL | 5.5 | 4.99 |
| Portsmouth, NH-ME | 3.7 | 4.99 |
| Santa Cruz-Watsonville, CA | 5.2 | 4.95 |
| Camden, NJ | 6.3 | 4.95 |
| Detroit-Livonia-Dearborn, MI | 7.3 | 4.94 |
| Champaign-Urbana, IL | 6.3 | 4.91 |
| Warren-Troy-Farmington Hills, MI | 5.9 | 4.91 |
| Lake County-Kenosha County, IL-WI | 4.7 | 4.91 |
| Atlantic City-Hammonton, NJ | 5.4 | 4.84 |
| Poughkeepsie-Newburgh-Middletown, NY | 6.2 | 4.82 |
| Kennewick-Pasco-Richland, WA | 5.0 | 4.82 |
| Providence-Fall River-Warwick, RI-MA | 6.7 | 4.80 |
| Rochester, MN | 16.0 | 4.80 |
| Palm Bay-Melbourne-Titusville, FL | 6.9 | 4.79 |
| Santa Rosa-Petaluma, CA | 5.9 | 4.78 |
| Richmond, VA | 6.0 | 4.78 |
| Colorado Springs, CO | 5.3 | 4.78 |
| Peoria, IL | 7.6 | 4.76 |
| Worcester, MA-CT | 7.7 | 4.75 |
| Danbury, CT | 5.3 | 4.74 |
| Bakersfield-Delano, CA | 6.7 | 4.72 |
| Napa, CA | 4.4 | 4.72 |
| New Haven, CT | 6.5 | 4.71 |
| Columbus, OH | 7.4 | 4.71 |
| Columbus, IN | 6.0 | 4.70 |
| Kansas City, MO-KS | 4.3 | 4.70 |
| Norwich-New London, CT-RI | 6.2 | 4.69 |
| Phoenix-Mesa-Glendale, AZ | 5.5 | 4.69 |
| St. Louis, MO-IL | 5.3 | 4.68 |
| Milwaukee-Waukesha-West Allis, WI | 6.9 | 4.67 |
| Charlottesville, VA | 5.9 | 4.66 |
| Dayton, OH | 9.0 | 4.65 |
| Honolulu, HI | 7.5 | 4.64 |
| Albany-Schedy-Troy, NY | 5.0 | 4.64 |
| Portland-Vancouver-Hillsboro, OR-WA | 6.3 | 4.62 |
| San Luis Obispo-Paso Robles, CA | 5.0 | 4.62 |
| Springfield, IL | 5.3 | 4.62 |
| Riverside-San Bernardino-Ontario, CA | 8.7 | 4.62 |
| Bloomington-Normal, IL | 5.5 | 4.62 |
| Fort Worth-Arlington, TX | 4.8 | 4.61 |
| Cincinnati-Middletown, OH-KY-IN | 5.3 | 4.60 |
| Manchester, NH | 6.5 | 4.59 |
| Taunton-Norton-Raynham, MA | 6.2 | 4.58 |
| Salt Lake City, UT | 5.2 | 4.58 |
| Syracuse, NY | 5.0 | 4.57 |
| Rochester-Dover, NH-ME | 6.5 | 4.57 |
| Anchorage, AK | 5.3 | 4.57 |
| Lawrence-Methuen-Salem, MA-NH | 5.6 | 4.57 |
| Madison, WI | 8.8 | 4.56 |
| Madera-Chowchilla, CA | 5.9 | 4.56 |
| Vineland-Millville-Bridgeton, NJ | 7.8 | 4.56 |
| Virginia Beach-Norfolk-Newport News, VA-NC | 6.5 | 4.56 |
| Salinas, CA | 5.8 | 4.56 |
| Ames, IA | 4.1 | 4.54 |
| Indianapolis-Carmel, IN | 5.3 | 4.54 |
| Warner Robins, GA | 7.1 | 4.53 |
| College Station-Bryan, TX | 4.8 | 4.52 |
| Iowa City, IA | 5.0 | 4.52 |
| Peabody, MA | 5.9 | 4.51 |
| Hanford-Corcoran, CA | 9.1 | 4.51 |
| Pittsfield, MA | 8.4 | 4.51 |
| Modesto, CA | 7.7 | 4.50 |
| Brockton-Bridgewater-Easton, MA | 8.9 | 4.50 |
| Albuquerque, NM | 5.9 | 4.49 |
| Miami-Miami Beach-Kendall, FL | 7.0 | 4.48 |
| Ithaca, NY | 6.3 | 4.48 |
| Gainesville, FL | 6.2 | 4.48 |
| Pittsburgh, PA | 10.7 | 4.46 |
| Cleveland-Elyria-Mentor, OH | 6.7 | 4.46 |
| Crestview-Fort Walton Beach-Destin, FL | 7.5 | 4.46 |
| Des Moines-West Des Moines, IA | 5.3 | 4.46 |
| Fayetteville-Springdale-Rogers, AR-MO | 5.2 | 4.45 |
| Birmingham-Hoover, AL | 4.6 | 4.45 |
| Charleston-North Charleston-Summerville, SC | 7.8 | 4.44 |
| El Centro, CA | 7.5 | 4.44 |
| Gary, IN | 3.9 | 4.43 |
| Binghamton, NY | 6.6 | 4.43 |
| Rochester, NY | 6.4 | 4.43 |
| Cedar Rapids, IA | 6.4 | 4.43 |
| Fort Lauderdale-Pompano Beach-Deerfield Beach, FL | 5.0 | 4.43 |
| San Antonio-New Braunfels, TX | 5.8 | 4.42 |
| West Palm Beach-Boca Raton-Boynton Beach, FL | 5.9 | 4.42 |
| Buffalo-Niagara Falls, NY | 6.3 | 4.42 |
| Harrisburg-Carlisle, PA | 6.2 | 4.39 |
| Waterbury, CT | 5.9 | 4.37 |
| Chico, CA | 7.8 | 4.37 |
| Springfield, MA-CT | 7.9 | 4.37 |
| State College, PA | 7.0 | 4.37 |
| Beaumont-Port Arthur, TX | 5.1 | 4.36 |
| Winston-Salem, NC | 5.1 | 4.36 |
| Las Cruces, NM | 8.9 | 4.36 |
| Barnstable Town, MA | 5.5 | 4.36 |
| Stockton, CA | 7.0 | 4.35 |
| Oklahoma City, OK | 5.5 | 4.35 |
| New Orleans-Metairie-Kenner, LA | 6.4 | 4.34 |
| New Bedford, MA | 6.1 | 4.34 |
| Augusta-Richmond County, GA-SC | 7.6 | 4.34 |
| Knoxville, TN | 8.6 | 4.33 |
| Lansing-East Lansing, MI | 6.9 | 4.32 |
| Bremerton-Silverdale, WA | 5.8 | 4.32 |
| Savannah, GA | 5.8 | 4.32 |
| Tucson, AZ | 6.2 | 4.32 |
| Allentown-Bethlehem-Easton, PA-NJ | 6.6 | 4.32 |
| Provo-Orem, UT | 6.9 | 4.31 |
| Yuba City, CA | 4.7 | 4.30 |
| Carson City, NV | 5.6 | 4.30 |
| Saginaw-Saginaw Township North, MI | 6.7 | 4.30 |
| Reno-Sparks, NV | 8.6 | 4.29 |
| Omaha-Council Bluffs, NE-IA | 4.9 | 4.29 |
| Haverhill-North Andover-Amesbury, MA-NH | 6.5 | 4.29 |
| Akron, OH | 5.7 | 4.29 |
| Morgantown, WV | 6.7 | 4.28 |
| Las Vegas-Paradise, NV | 10.1 | 4.28 |
| Baton Rouge, LA | 4.1 | 4.27 |
| Tampa-St. Petersburg-Clearwater, FL | 5.9 | 4.27 |
| Nashville-Davidson–Murfreesboro–Franklin, TN | 6.7 | 4.27 |
| Fresno, CA | 6.8 | 4.27 |
| Wichita, KS | 5.1 | 4.26 |
| Boise City-Nampa, ID | 5.7 | 4.26 |
| Pascagoula, MS | 6.0 | 4.26 |
| Brunswick, GA | 6.2 | 4.26 |
| Monroe, MI | 5.9 | 4.25 |
| Redding, CA | 5.1 | 4.25 |
| Wilmington, NC | 6.9 | 4.25 |
| Hagerstown-Martinsburg, MD-WV | 6.6 | 4.25 |
| Little Rock-North Little Rock-Conway, AR | 6.1 | 4.24 |
| Montgomery, AL | 8.2 | 4.24 |
| Jacksonville, FL | 5.6 | 4.24 |
| Greenville-Mauldin-Easley, SC | 6.1 | 4.23 |
| Fayetteville, NC | 5.4 | 4.23 |
| Leominster-Fitchburg-Gardner, MA | 7.4 | 4.22 |
| Winchester, VA-WV | 7.6 | 4.22 |
| Tulsa, OK | 8.6 | 4.22 |
| Chattanooga, TN-GA | 5.7 | 4.22 |
| Elmira, NY | 7.6 | 4.22 |
| Kalamazoo-Portage, MI | 8.0 | 4.21 |
| Columbia, MO | 6.5 | 4.21 |
| Memphis, TN-MS-AR | 9.0 | 4.21 |
| Portland-South Portland-Biddeford, ME | 6.4 | 4.21 |
| Blacksburg-Christiansburg-Radford, VA | 6.8 | 4.20 |
| Ogden-Clearfield, UT | 4.6 | 4.20 |
| Decatur, AL | 4.5 | 4.20 |
| Fairbanks, AK | 5.2 | 4.19 |
| Greensboro-High Point, NC | 5.6 | 4.19 |
| Louisville-Jefferson County, KY-IN | 5.4 | 4.19 |
| Flint, MI | 6.5 | 4.18 |
| Columbia, SC | 9.5 | 4.17 |
| Victoria, TX | 6.5 | 4.17 |
| Tallahassee, FL | 7.0 | 4.17 |
| Bay City, MI | 5.7 | 4.17 |
| Battle Creek, MI | 7.0 | 4.17 |
| Burlington-South Burlington, VT | 6.6 | 4.17 |
| Merced, CA | 6.6 | 4.16 |
| Grand Rapids-Wyoming, MI | 3.7 | 4.16 |
| Corpus Christi, TX | 6.4 | 4.16 |
| Kingston, NY | 5.4 | 4.15 |
| Greenville, NC | 6.5 | 4.15 |
| Odessa, TX | 9.6 | 4.15 |
| Lexington-Fayette, KY | 4.2 | 4.14 |
| Jackson, MS | 6.9 | 4.14 |
| Houma-Bayou Cane-Thibodaux, LA | 7.7 | 4.14 |
| Macon, GA | 4.9 | 4.14 |
| Tuscaloosa, AL | 7.7 | 4.14 |
| Manhattan, KS | 7.2 | 4.14 |
| Niles-Benton Harbor, MI | 5.4 | 4.13 |
| Dover, DE | 6.4 | 4.13 |
| Ocean City, NJ | 6.0 | 4.13 |
| Salisbury, MD | 5.9 | 4.13 |
| Columbus, GA-AL | 7.9 | 4.13 |
| Jackson, MI | 6.0 | 4.12 |
| Tyler, TX | 7.9 | 4.12 |
| St. Cloud, MN | 9.2 | 4.11 |
| Duluth, MN-WI | 7.1 | 4.11 |
| Cheyenne, WY | 7.5 | 4.11 |
| Farmington, NM | 6.2 | 4.10 |
| Tacoma, WA | 4.4 | 4.10 |
| Yuma, AZ | 6.8 | 4.10 |
| York-Hanover, PA | 4.6 | 4.09 |
| Parkersburg-Marietta-Vienna, WV-OH | 6.1 | 4.09 |
| Mobile, AL | 7.5 | 4.09 |
| Orlando-Kissimmee-Sanford, FL | 6.7 | 4.09 |
| Appleton, WI | 5.1 | 4.08 |
| Waco, TX | 4.5 | 4.08 |
| Reading, PA | 5.1 | 4.08 |
| Roanoke, VA | 6.2 | 4.08 |
| Utica-Rome, NY | 8.0 | 4.07 |
| Amarillo, TX | 6.9 | 4.07 |
| Eau Claire, WI | 6.4 | 4.07 |
| Lafayette, IN | 7.1 | 4.06 |
| Toledo, OH | 7.3 | 4.06 |
| Davenport-Moline-Rock Island, IA-IL | 6.6 | 4.06 |
| Cumberland, MD-WV | 5.9 | 4.06 |
| Elizabethtown, KY | 7.2 | 4.05 |
| Rockford, IL | 6.2 | 4.05 |
| Albany, GA | 6.7 | 4.05 |
| Lincoln, NE | 7.3 | 4.05 |
| Athens-Clarke County, GA | 5.8 | 4.04 |
| Bloomington, IN | 6.7 | 4.04 |
| Billings, MT | 5.9 | 4.04 |
| Rome, GA | 7.3 | 4.04 |
| Lawrence, KS | 12.4 | 4.03 |
| Muncie, IN | 4.7 | 4.03 |
| Laredo, TX | 7.8 | 4.03 |
| Johnstown, PA | 3.9 | 4.03 |
| Auburn-Opelika, AL | 8.5 | 4.03 |
| Holland-Grand Haven, MI | 5.4 | 4.03 |
| Olympia, WA | 3.5 | 4.03 |
| Charleston, WV | 5.0 | 4.02 |
| Mankato-North Mankato, MN | 7.2 | 4.02 |
| Grand Junction, CO | 6.7 | 4.02 |
| Killeen-Temple-Fort Hood, TX | 6.9 | 4.02 |
| Topeka, KS | 8.2 | 4.01 |
| El Paso, TX | 7.2 | 4.01 |
| Sherman-Denison, TX | 5.1 | 4.01 |
| Flagstaff, AZ | 9.1 | 4.01 |
| Janesville, WI | 6.8 | 4.00 |
| Williamsport, PA | 6.6 | 4.00 |
| Greeley, CO | 5.9 | 4.00 |
| South Bend-Mishawaka, IN-MI | 4.7 | 3.99 |
| Racine, WI | 6.1 | 3.99 |
| Huntington-Ashland, WV-KY-OH | 5.4 | 3.99 |
| Decatur, IL | 10.5 | 3.99 |
| Evansville, IN-KY | 7.1 | 3.99 |
| Wausau, WI | 6.5 | 3.98 |
| Fond du Lac, WI | 5.4 | 3.98 |
| Fort Wayne, IN | 5.6 | 3.97 |
| Spartanburg, SC | 7.0 | 3.97 |
| Prescott, AZ | 6.1 | 3.97 |
| Green Bay, WI | 6.1 | 3.97 |
| Sheboygan, WI | 5.2 | 3.96 |
| Gainesville, GA | 3.6 | 3.96 |
| Pueblo, CO | 6.8 | 3.95 |
| Lafayette, LA | 8.5 | 3.95 |
| Naples-Marco Island, FL | 5.9 | 3.94 |
| Erie, PA | 5.9 | 3.94 |
| Missoula, MT | 6.7 | 3.94 |
| Bowling Green, KY | 7.5 | 3.93 |
| Kankakee-Bradley, IL | 6.4 | 3.93 |
| Visalia-Porterville, CA | 8.3 | 3.93 |
| Bangor, ME | 4.8 | 3.92 |
| Hinesville-Fort Stewart, GA | 8.2 | 3.92 |
| Terre Haute, IN | 5.8 | 3.92 |
| Florence, SC | 6.8 | 3.91 |
| Steubenville-Weirton, OH-WV | 8.6 | 3.91 |
| San Angelo, TX | 8.0 | 3.91 |
| Oshkosh-Neenah, WI | 6.6 | 3.91 |
| Salem, OR | 5.7 | 3.91 |
| Shreveport-Bossier City, LA | 5.4 | 3.90 |
| Glens Falls, NY | 7.8 | 3.90 |
| Springfield, MO | 7.6 | 3.90 |
| Canton-Massillon, OH | 7.3 | 3.90 |
| Lake Charles, LA | 7.1 | 3.90 |
| Eugene-Springfield, OR | 6.2 | 3.90 |
| Gulfport-Biloxi, MS | 5.6 | 3.89 |
| Lancaster, PA | 6.2 | 3.89 |
| Casper, WY | 5.5 | 3.89 |
| Bellingham, WA | 5.3 | 3.88 |
| Pocatello, ID | 4.6 | 3.87 |
| Lynchburg, VA | 6.4 | 3.87 |
| Bend, OR | 6.3 | 3.87 |
| Longview, WA | 6.5 | 3.87 |
| Pensacola-Ferry Pass-Brent, FL | 5.6 | 3.86 |
| Lubbock, TX | 7.3 | 3.86 |
| Grand Forks, ND-MN | 7.3 | 3.86 |
| Muskegon-Norton Shores, MI | 6.6 | 3.86 |
| Fargo, ND-MN | 7.0 | 3.86 |
| Lima, OH | 6.1 | 3.86 |
| Longview, TX | 8.7 | 3.85 |
| Danville, IL | 6.0 | 3.85 |
| Scranton–Wilkes-Barre, PA | 6.6 | 3.85 |
| North Port-Bradenton-Sarasota, FL | 6.6 | 3.84 |
| Mount Vernon-Anacortes, WA | 6.9 | 3.84 |
| Clarksville, TN-KY | 5.6 | 3.83 |
| Abilene, TX | 5.6 | 3.83 |
| Lawton, OK | 7.7 | 3.83 |
| Johnson City, TN | 6.8 | 3.82 |
| La Crosse, WI-MN | 10.9 | 3.82 |
| Kingsport-Bristol-Bristol, TN-VA | 7.8 | 3.81 |
| Springfield, OH | 6.1 | 3.81 |
| Michigan City-La Porte, IN | 5.4 | 3.81 |
| Port St. Lucie, FL | 6.4 | 3.80 |
| Lake Havasu City-Kingman, AZ | 7.6 | 3.80 |
| Rocky Mount, NC | 6.0 | 3.79 |
| Alexandria, LA | 9.9 | 3.79 |
| Spokane, WA | 6.4 | 3.78 |
| Youngstown-Warren-Boardman, OH-PA | 6.8 | 3.78 |
| Cape Coral-Fort Myers, FL | 6.5 | 3.78 |
| Valdosta, GA | 7.1 | 3.77 |
| Medford, OR | 6.6 | 3.77 |
| Wenatchee-East Wenatchee, WA | 6.2 | 3.77 |
| Coeur d'Alene, ID | 6.5 | 3.76 |
| Panama City-Lynn Haven-Panama City Beach, FL | 6.2 | 3.76 |
| Lebanon, PA | 6.2 | 3.76 |
| Bismarck, ND | 7.6 | 3.76 |
| St. Joseph, MO-KS | 6.9 | 3.75 |
| McAllen-Edinburg-Mission, TX | 6.1 | 3.75 |
| Cleveland, TN | 6.4 | 3.72 |
| Asheville, NC | 8.6 | 3.71 |
| Idaho Falls, ID | 5.7 | 3.71 |
| Burlington, NC | 7.8 | 3.71 |
| Jacksonville, NC | 5.4 | 3.71 |
| Waterloo-Cedar Falls, IA | 5.6 | 3.71 |
| Pine Bluff, AR | 6.4 | 3.70 |
| Altoona, PA | 8.0 | 3.69 |
| Dubuque, IA | 5.4 | 3.67 |
| Santa Fe, NM | 4.8 | 3.67 |
| Sumter, SC | 7.2 | 3.67 |
| Anderson, IN | 7.1 | 3.66 |
| Sandusky, OH | 6.0 | 3.66 |
| Sioux Falls, SD | 8.8 | 3.66 |
| Jefferson City, MO | 6.1 | 3.66 |
| Punta Gorda, FL | 9.3 | 3.66 |
| Cape Girardeau-Jackson, MO-IL | 9.9 | 3.65 |
| Florence-Muscle Shoals, AL | 6.8 | 3.65 |
| Dothan, AL | 9.4 | 3.65 |
| Mansfield, OH | 6.4 | 3.64 |
| Sebastian-Vero Beach, FL | 7.2 | 3.64 |
| Lakeland-Winter Haven, FL | 6.1 | 3.63 |
| Logan, UT-ID | 4.2 | 3.63 |
| Great Falls, MT | 7.5 | 3.62 |
| Wheeling, WV-OH | 7.8 | 3.62 |
| Lewiston-Auburn, ME | 7.2 | 3.61 |
| Brownsville-Harlingen, TX | 5.6 | 3.61 |
| Wichita Falls, TX | 7.2 | 3.60 |
| Hot Springs, AR | 8.1 | 3.59 |
| Dalton, GA | 3.3 | 3.59 |
| Hattiesburg, MS | 9.8 | 3.58 |
| Owensboro, KY | 6.7 | 3.58 |
| Harrisonburg, VA | 4.9 | 3.57 |
| Ocala, FL | 7.4 | 3.56 |
| Jackson, TN | 9.7 | 3.56 |
| Lewiston, ID-WA | 7.0 | 3.56 |
| Joplin, MO | 7.2 | 3.56 |
| Gadsden, AL | 9.1 | 3.54 |
| Elkhart-Goshen, IN | 3.6 | 3.54 |
| Rapid City, SD | 7.7 | 3.54 |
| Monroe, LA | 8.4 | 3.54 |
| Anderson, SC | 7.7 | 3.53 |
| Texarkana-Texarkana, TX-AR | 7.0 | 3.53 |
| Yakima, WA | 6.3 | 3.52 |
| Fort Smith, AR-OK | 5.7 | 3.52 |
| Goldsboro, NC | 5.6 | 3.51 |
| Deltona-Daytona Beach-Ormond Beach, FL | 7.4 | 3.51 |
| Anniston-Oxford, AL | 5.9 | 3.51 |
| Sioux City, IA-NE-SD | 5.7 | 3.51 |
| St. George, UT | 6.1 | 3.49 |
| Danville, VA | 5.2 | 3.46 |
| Jonesboro, AR | 7.8 | 3.42 |
| Hickory-Lenoir-Morganton, NC | 7.0 | 3.41 |
| Myrtle Beach-North Myrtle Beach-Conway, SC | 4.4 | 3.39 |
| Palm Coast, FL | 6.1 | 3.34 |
| Morristown, TN | 5.6 | 3.28 |
| Source: U.S. Bureau of Labor Statistics. | ||
Table 6 shows the 10 MSAs with the largest 90–10 ratios and the employment shares for selected high-paying occupations. Although healthcare practitioners and technical occupations are not shown in this table, 8 of the 10 MSAs have below-average employment in this occupational group. The table shows that the areas with the highest 90–10 ratios tend to have higher-than-average shares of employment in the high-paying occupational groups. All of the areas have above-average employment shares in computer and mathematical occupations and in business and financial occupations. Four of the 10 areas with the highest 90–10 ratios have an above-average percentage of employment in all 7 of the high-paying occupational groups, and 8 of the 10 areas have above-average employment in at least 5 of the high-paying groups.
Some of the areas shown in table 6 have the largest concentrations of employment in high-paying occupational groups in the entire country. Among the 395 metropolitan statistical areas covered in this study, San Jose-Sunnyvale-Santa Clara has the highest percentage of employment in management and computer and mathematical occupations. Washington-Arlington-Alexandria ranks first in the nation in business and financial operations and legal occupations. Huntsville has the highest percentage of employment in the architecture and engineering group. Bridgeport-Stamford-Norwalk ranked second nationally in management occupations, and Durham-Chapel Hill ranked second in life, physical, and social science occupations. There is a clear relationship between employment in high-paying occupations and the 90–10 ratio. Areas with the highest 90–10 ratios tend to have employment concentrated in at least some of the highest paying occupational groups.
| Area | All-occupations employment | Percent of all-occupations employment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Management | Business and financial operations | Computer and math-ematical | Architecture and engineering | Life, physical, and social science | Legal | Arts, design, enter-tainment, sports, and media | |||
| United States | 4.86 | 132,588,810 | 4.9 | 5.0 | 2.8 | 1.8 | 0.9 | 0.8 | 1.3 |
| San Jose-Sunnyvale-Santa Clara, CA | 7.14 | 930,070 | 8.3 | 6.9 | 10.5 | 5.7 | 1.1 | 0.9 | 1.4 |
| Washington-Arlington-Alexandria, DC-VA-MD-WV | 6.76 | 2,367,240 | 7.7 | 10.8 | 8.0 | 2.2 | 1.8 | 2.7 | 2.2 |
| Bethesda-Rockville-Frederick, MD | 6.29 | 561,830 | 7.2 | 8.2 | 5.9 | 2.4 | 2.8 | 0.9 | 1.7 |
| New York-White Plains-Wayne, NY-NJ | 6.28 | 5,242,070 | 5.6 | 6.7 | 3.1 | 0.9 | 0.7 | 1.4 | 2.8 |
| Huntsville, AL | 6.16 | 210,110 | 4.5 | 7.6 | 6.5 | 7.6 | 0.7 | 0.4 | 1.0 |
| San Francisco-San Mateo-Redwood City, CA | 6.15 | 1,045,700 | 7.5 | 8.4 | 6.6 | 1.9 | 2.0 | 1.4 | 2.5 |
| Oakland-Fremont-Hayward, CA | 6.03 | 1,003,860 | 6.4 | 6.2 | 4.0 | 3.0 | 1.7 | 0.7 | 1.4 |
| Bridgeport-Stamford-Norwalk, CT | 6.00 | 420,170 | 8.2 | 7.1 | 3.3 | 1.5 | 0.7 | 0.8 | 2.0 |
| Durham-Chapel Hill, NC | 5.76 | 276,580 | 5.7 | 6.2 | 6.4 | 2.2 | 3.8 | 0.6 | 1.3 |
| Boulder, CO | 5.68 | 163,010 | 5.0 | 7.4 | 6.7 | 3.9 | 3.3 | 0.8 | 2.2 |
| Source: U.S. Bureau of Labor Statistics. | |||||||||
Table 7 shows the 10 MSAs with the lowest 90–10 ratios. Each of the areas has relatively low levels of employment in the high-paying occupational groups and relatively high levels of employment in the lower paying occupational groups. In addition, these metropolitan areas are small and located in geographic areas where wages are typically lower, further suggesting that size and location are factors in the 90–10 wage ratio.
| Area | All-occupations employment | Percent of all-occupations employment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Management | Business and financial operations | Computer and math-ematical | Architecture and engineering | Life, physical, and social science | Legal | Arts, design, enter-tainment, sports, and media | |||
| United States | 4.86 | 132,588,810 | 4.9 | 5.0 | 2.8 | 1.8 | 0.9 | 0.8 | 1.3 |
| Morristown, TN | 3.28 | 43,970 | 4.1 | 1.8 | 0.7 | 1.3 | 0.3 | * | 0.6 |
| Palm Coast, FL | 3.34 | 18,950 | 2.2 | 2.6 | 1.2 | 0.6 | 0.2 | 0.4 | 0.4 |
| Myrtle Beach-North Myrtle Beach-Conway, SC | 3.39 | 112,720 | 3.8 | 2.3 | 0.7 | 0.5 | 0.2 | 0.6 | 1.2 |
| Hickory-Lenoir-Morganton, NC | 3.41 | 143,700 | 3.4 | 2.3 | 0.8 | 0.9 | 0.4 | 0.3 | 0.5 |
| Jonesboro, AR | 3.42 | 50,350 | 4.2 | 2.1 | 0.7 | 0.6 | 0.3 | 0.4 | 0.5 |
| Danville, VA | 3.46 | 37,000 | 2.6 | 2.1 | 0.6 | 0.6 | 0.3 | 0.4 | 0.5 |
| St. George, UT | 3.49 | 49,730 | 4.1 | 2.5 | 0.9 | 0.7 | 0.6 | 0.7 | 1.0 |
| Sioux City, IA-NE-SD | 3.51 | 71,070 | 3.6 | 3.2 | 1.4 | 0.7 | 0.4 | 0.4 | 0.9 |
| Anniston-Oxford, AL | 3.51 | 43,150 | 2.7 | 2.6 | 0.8 | 1.5 | 0.3 | 0.4 | 1.0 |
| Deltona-Daytona Beach-Ormond Beach, FL | 3.51 | 152,950 | 2.3 | 3.6 | 1.1 | 1.0 | 0.4 | 0.8 | 0.9 |
| * The employment estimate for legal occupations in Morristown, TN, was not published in May 2013. Source: U.S. Bureau of Labor Statistics. | |||||||||
This analysis shows that location, size, and occupational composition all play important roles in determining the level of wage inequality within and across U.S. metropolitan areas. Large areas, especially in the Northeast and on the West Coast, typically have higher 90–10 ratios (greater disparity between the highest paid and lowest paid workers), while those in the South and Midwest tend to have lower ratios. In addition, areas with high 90–10 ratios tend to have employment concentrated in high-paying occupations, while those with lower ratios have less concentration in such occupations.
?pagebreak>?pagebreak>?pagebreak>?pagebreak>J. Chris Cunningham, "Measuring wage inequality within and across U.S. metropolitan areas, 2003–13," Monthly Labor Review, U.S. Bureau of Labor Statistics, September 2015, https://doi.org/10.21916/mlr.2015.35
1 Some areas cannot be compared over time because of changes in the composition of the area and thus are excluded here.
2 The R2 value, also known as the coefficient of determination, indicates how well the plotted points fit a linear trend line. The R2 value ranges from 0 to 1. The closer the value is to 1, the better the plots fit the line or the stronger the linear relationship is between the two variables. The R2 value will always be positive, regardless of the whether the slope of the linear trend line is positive or negative.