An official website of the United States government
 United States Department of Labor
United States Department of Labor
By Thomas D. Evans and Connor J. Doherty
Thomas D. Evans and Connor J. Doherty are mathematical statisticians on the Statistical Methods Staff, Office of Employment and Unemployment Statistics, Bureau of Labor Statistics.
Short-run movements in labor force time series are strongly influenced by seasonality—periodic fluctuations associated with recurring calendar-related events such as weather, holidays, and the opening and closing of schools. Seasonal adjustment removes the influence of these fluctuations and makes it easier for users to observe fundamental changes in the level of the series, particularly changes associated with general economic expansions and contractions.
Seasonal adjustment is feasible only if the seasonal effects are reasonably stable with respect to timing, direction, and magnitude. These effects are not necessarily fixed and often evolve over time. The evolving patterns are estimated by the X-13ARIMA-SEATS (X-13) program, with procedures based on "filters" that successively average a shifting timespan of data, thereby providing estimates of seasonal factors that change in a smooth fashion from year to year.
For observations in the middle of a series, a set of symmetric moving averages with fixed weights produces final seasonally adjusted estimates. A filter is symmetric if it is centered around the time point being adjusted, with an equal amount of data preceding and following that point. Standard seasonal adjustment options imply a symmetric filter that uses from 6 to 10 years of original data to produce a final seasonally adjusted estimate. This final adjustment can be made only when there are enough data beyond the time point in question to adjust with a symmetric filter.
To seasonally adjust recent data, shorter filters with less desirable properties must be used. These asymmetric filters use fewer observations after the reference point than preceding it. The weights for such filters vary with the number of observations that are available beyond the time point for which estimates are to be adjusted.
Seasonally adjusted data for the current year are produced with a technique known as concurrent adjustment. Under this practice, the current month's seasonally adjusted estimate is computed using all relevant original data up to and including data for the current month.
Each time an observation is added, previous estimates are revised. The number of estimates that are revised depends on the filter. Revisions to a seasonally adjusted estimate for a given time point continue until enough future observations become available to use the symmetric weights. This effectively means waiting up to 5 years for a final adjustment when standard options are used.
At the end of each calendar year, the Bureau of Labor Statistics (BLS) reestimates the seasonal factors for the Current Population Survey (CPS, or household survey) time series by including another full year of data in the adjustment process. On the basis of this annual reestimation, BLS revises historical seasonally adjusted data for the previous 5 years. As a result, each year's data are generally subject to five revisions before the values are considered final. The fifth and final revisions to data for the earliest of the 5 years are usually quite small, while the first-time revisions to data for the most recent years are generally much larger. For the major aggregate labor force series, however, the first-time revisions rarely alter the essential trends observed in the initial estimates.
Beginning in 2003, BLS adopted X-12-ARIMA as the official seasonal adjustment program for national CPS labor force series, replacing the X-11-ARIMA program that had been used since 1980. Both X-12-ARIMA and X-11-ARIMA incorporate earlier versions of the widely used X-11 method developed at the U.S. Census Bureau in the 1960s.1 Statistics Canada added to the X-11 method the ability to extend the time series with forward and backward extrapolations from Auto-Regressive Integrated Moving Average (ARIMA) models, prior to seasonal adjustment. The X-11 algorithm for seasonal adjustment is then applied to the extended series. When adjusted data are revised after future data become available, the use of forward extension results in initial seasonal adjustments that are subject to smaller revisions, on average.
The enhancements in the X-12-ARIMA program fall into three basic categories:
Starting in 2015, BLS began using the X-13ARIMA-SEATS program,2 which was developed by the U.S. Census Bureau. The X-13ARIMA-SEATS program includes all of the capabilities of the X-12-ARIMA program, while adding the SEATS seasonal adjustment methodology developed at the Bank of Spain.3
The X-11 and SEATS methods have many similarities. The ARIMA model of the observed series is the starting point for both. They both also use the same basic estimator, which is a weighted moving average of the series to produce the seasonally adjusted output. Their methods differ in the derivation of moving average weights. (For more information, see the section X-11 and SEATS Decompositions below.)
The X-11 method is empirically based. It directly selects the seasonal moving averages from a pre-specified set. The weights are not designed for any specific series but fit a wide variety of series. SEATS is model-based and derives a moving average from the ARIMA model of the series. The moving averages are tailored to the specific modeled properties of the series. The SEATS methodology is flexible in that it can adjust some series that the X-11 method finds too variable. It also facilitates analysis with a variety of error measures produced within the system.
For the national CPS labor force series that are seasonally adjusted by BLS, the main steps of the seasonal adjustment process proceed in the following order:
Time series models play an important role in seasonal adjustment. They are used to identify and adjust the series for atypical observations and other external effects, as well as to extend the original series with backcasts and forecasts so that fewer asymmetric filters can be used at the beginning and end of the series.
ARIMA models4 are designed to make forecasts of a time series based on only its past values. While these models can represent a wide class of evolving time series patterns, they do not account for the presence of occasional outliers and other special external effects. An outlier represents a sudden break in the normal evolutionary behavior of a time series. Ignoring the existence of outliers may lead to serious distortions in the seasonally adjusted series.
A common form of outlier that presents a special problem for seasonal adjustment is an abrupt shift in the level of the data that may be either transitory or permanent. Three types of outliers are usually distinguished:
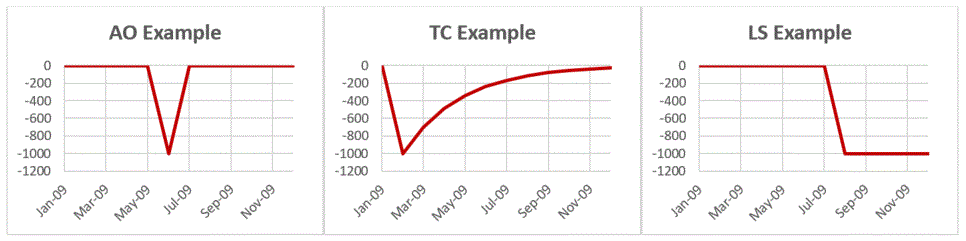
These three main types of outliers, as well as other types of external effects, may be handled by the time series modeling component of the X-13ARIMA-SEATS program. This is done by adding to the ARIMA model appropriately defined regression variables based on intervention analysis originally proposed by George E.P. Box and George C. Tiao.5
The combined regression and ARIMA model is referred to as a regARIMA model and is represented by
(1-B )d (1-B s)D Yt = ∑i βi (1-B )d (1-B s)D xit + wt
where:
While the ARIMA model can be very complicated theoretically, in practice it takes a parsimonious form involving only a few estimated parameters. There are well-developed methods for determining the number and types of parameters and the degree of differencing appropriate for a given series.
With respect to specifying the regression component to control for outliers, the X-13ARIMA-SEATS program offers two approaches. First, major external events, such as breaks in trend, are usually associated with known events. In such cases, the user has sufficient prior information to specify special regression variables to estimate and control for these effects.
Second, X-13ARIMA-SEATS also offers automatic outlier detection to specify the regression component because it is rare to have sufficient prior information to be able to locate and identify all of the atypical observations that may exist in a time series.7 This approach is especially useful when a large number of series must be processed. Of course, both approaches may be combined so that readily available prior information can be used directly, while unknown substantial outliers may still be discovered.
The preference is to use relatively long series in fitting time series models, but with some qualifications. Sometimes, the relevance of data in the distant past to seasonal adjustment is questionable, which may lead to using a shorter series.
Even though the filters have limited memory, there are reasons for using longer series. First, for homogenous time series, the more data used to identify and estimate a model, the more likely it is that the model will represent the structure of the data well and the more accurate the parameter estimates will be. The exact amount of data needed for time series modeling depends on the properties of the series involved. Arbitrarily truncating the series, however, may lead to more frequent changes in model identification and to large changes in estimated parameters, which in turn may lead to larger-than-necessary revisions in forecasts.
Second, although level shifts and other types of outliers tend to occur more often in longer series, the X-13ARIMA-SEATS program has the capability of automatically controlling for these effects. Third, some useful diagnostics available in X-13ARIMA-SEATS typically require a minimum of 11 years of data and, in some cases, as much as 14 years of data. Finally, attempting to fit longer series often provides useful insights into the properties of the series, including their overall quality and the effects of major changes in survey design.
Intervention analysis is used extensively to estimate the magnitude of known breaks in CPS series and of automatic outlier detection to identify and correct for the presence of additional atypical observations. Once a model is estimated, it is evaluated in terms of its adequacy for seasonal adjustment purposes. The criteria essentially require a model to fit the series well (there should be no systematic patterns in the residuals) and to have low average forecasting errors for the last 3 years of observed data. When there is a tradeoff between the length of the series and the adequacy of the model, a shorter series is selected. In this case, the identification of the model is not changed with the addition of new data unless the model fails diagnostic testing.
Acceptable regARIMA models have been developed for all of the CPS labor force series that are directly adjusted. (For information about directly and indirectly adjusted series, see section 3 on Aggregation procedures below.)
Prior adjustments are adjustments made to the original data prior to seasonal adjustment. Their purpose is to adjust the original series for atypical observations and other external effects that otherwise would seriously distort the estimates of the seasonal factors. Prior adjustment factors are subtracted from or used as divisors for the original series, depending on whether the seasonal adjustment is additive or multiplicative
Prior adjustment factors may be based on special user-defined adjustments or handled more formally with regARIMA modeling. Currently, all prior adjustment factors for the national household survey labor force series are estimated directly from regARIMA.
A type of outlier that occasionally occurs in CPS series is the permanent level shift. Most such shifts have been due to noneconomic methodological changes related to revisions in population controls and to major modifications to the CPS design.
Population estimates extrapolated from the latest decennial census are used in the second-stage estimation procedure to control CPS sample estimates to more accurate levels. These intercensal population estimates are regularly revised to reflect the latest information on population change.
During the 1990s, three major breaks occurred in the intercensal population estimates. Population controls based on the 1990 census, adjusted for the estimated undercount, were introduced into the CPS series in 1994 and, in 1996, were extended back to 1990. In January 1997 and January 1999, the population controls were revised to reflect updated information on net international migration.
Population revisions that reflected the results of Census 2000 were introduced with the release of data for January 2003 and were extended back to data beginning in January 2000. Since 2003, the population controls have been updated each January to reflect new estimates of net international migration, updated vital statistics and other information, and any methodological improvements in the population estimation process. The population updates introduced in January 2012 incorporated the results of the 2010 Census; those updates were not extended back to January 2010. The population updates introduced in January 2022 reflect the introduction of a blended 2020 population base, which combines population totals from the 2020 Census and demographic characteristics from other sources; those updates were not extended back to January 2020. Further information on CPS population controls for 1996 to the present is available in the CPS technical documentation.
In 1994, major changes to the CPS were introduced, including a redesigned and automated questionnaire and revisions to some of the labor force concepts and definitions. In January 2003, major changes to industry and occupational classifications also were introduced and were extended back to data beginning in 2000.
To test for the possibility that updates to the population controls or significant survey changes have important effects on those CPS series with large numerical revisions, each regARIMA model is modified to include intervention variables for those years. The coefficients for these variables provide estimates of the direction and magnitude of the intervention effects.
Intervention effects for 2000 were necessary for selected employment series related primarily to Hispanic, adult, and agricultural categories. These effects mainly reflect increases in adult and Hispanic employment due to the introduction of Census 2000-based population controls and a decline in agricultural employment caused by the change in the industry classification system.8
Due to an unusual revision in the population controls in January 2000, the unadjusted employment level of Black or African American men 20 years or over had a strong upward shift in the first quarter of 2000. This temporary effect was permanently removed from the seasonally adjusted series with the use of the regARIMA model.
At the end of 2001, series for unemployed job losers were identified as having had substantial upward level shifts one month after the September 11, 2001, terrorist attacks on the World Trade Center in New York City.9 Also, four additional series related to workers employed part time for economic reasons were identified as having substantial upward shifts at the time of the terrorist attacks.
Many CPS data series had large outliers after the onset of the coronavirus (COVID-19) pandemic. Since April 2020, BLS staff have tested CPS series for outliers each month to determine whether any changes were needed for the seasonal adjustment models. BLS staff determined that the vast majority of series had large outliers and made adjustments as needed to the models used in seasonal adjustment processing to account for them. While the sudden changes in CPS series due to the pandemic may at first appear to be permanent level shifts, the changes actually faded over time. Typically, a combination of TC and AO outliers is used to model the pandemic effects.
Seasonal adjustment factors can be either multiplicative or additive. A multiplicative seasonal effect is assumed to be proportional to the level of the series. A sudden large change in the level of the series will be accompanied by a proportionally large seasonal effect. In contrast, an additive seasonal effect is assumed to be unaffected by the level of the series. In times of relative economic stability, the multiplicative option is generally preferred over the additive option. However, in the presence of a large level shift in a time series, multiplicative seasonal adjustment factors can result in systematic over- or under-adjustment of the series; in such cases, additive seasonal adjustment factors are preferred since they tend to track seasonal fluctuations in the series more accurately and have smaller revisions.
Prior to April 2020, many seasonally adjusted CPS series used multiplicative seasonal adjustment factors. However, series were respecified as additive once a significant outlier was detected in the incoming data. By the end of 2020, nearly all directly adjusted series had been respecified as additive. In accordance with usual practice, the seasonal adjustment models and factors were reviewed at the end of the calendar year, and necessary changes were made to the seasonal adjustment settings as required. For the end-of-year review, temporary changes and level shifts were considered in addition to additive outliers; using all of these outlier types often makes the outlier sets more parsimonious.
Diagnostic tests show that the possibility of systematic over- or under-adjustments from multiplicative adjustment factors appears unlikely for most series beginning with data for 2021. Therefore, series with diagnostics that exhibit a strong need for multiplicative adjustment were changed back to multiplicative adjustment. Series with a strong need for additive adjustment were set to additive adjustment. Those series without a strong need had their adjustment mode reset to the mode used prior to April 2020.
Ten unemployment series have a hybrid adjustment based on strong pandemic effects that required additive adjustments. From April 2020 through December 2020, the historical factors are additive; the other months for these series have multiplicative factors. The 10 series are:
Calendar effects are temporary level shifts in a series that result from calendar events such as moving holidays or the differing composition of weekdays in a month between years. These effects have different influences on the same month across years, thereby distorting the normal seasonal patterns for the given month. Most CPS series show no holiday effects as most holidays do not fall in the reference week. In some years, Good Friday and Labor Day can fall in the reference week and affect the actual hours at work series, since holidays can lower the number of hours actually worked.
Federal government agencies were shut down or operating at reduced staffing levels during a lapse in appropriations from October 1, 2025, through November 12, 2025. All CPS operations, including data collection, were suspended during that time period. CPS data were not collected for October 2025 due to the federal government shutdown. However, the X-13ARIMA-SEATS program needs to have a complete time series in order to run. The program has the capability to estimate missing observations in the ARIMA model by supplying a large value at the point in question and treating it as an AO.10 The formula is
Ŷt0 = Yt0 - βt0 AOt (t0)
where:
The X-11 and SEATS methods of seasonal adjustment contained within the X-13ARIMA-SEATS program assume that the original series is composed of three components: trend-cycle, seasonal, and irregular. Depending on the relationship between the original series and each of the components, the mode of seasonal adjustment may be additive or multiplicative. Formal tests are conducted to determine the appropriate mode of adjustment.
The multiplicative mode assumes that the absolute magnitudes of the components of the series are dependent on each other, which implies that the size of the seasonal component increases and decreases with the level of the series. With this mode, the monthly seasonal factors are ratios, with all positive values centered around unity (1.0). The seasonally adjusted series values are computed by dividing each month's original value by the corresponding seasonal factor.
In contrast, the additive mode assumes that the absolute magnitudes of the components of the series are independent of each other, which implies that the size of the seasonal component is independent of the level of the series. In this case, the seasonal factors represent positive or negative deviations from the original series and are centered around zero. The seasonally adjusted series values are computed by subtracting the corresponding seasonal factor from each month's original value.
Most seasonally adjusted CPS series were previously adjusted using the X-11 component of the X-13ARIMA-SEATS program. The X-11 method applies a sequence of moving average and smoothing calculations to estimate the trend-cycle, seasonal, and irregular components. The method takes either a ratio-to- or difference-from-moving-average approach, depending on whether the multiplicative or additive model is used. For observations in the middle of the series, a set of fixed symmetric moving averages (filters) is used to produce final estimates. The implied length of the final filter under standard options is 72 time points for the 3 by 5 seasonal moving average or 120 time points for the 3 by 9 moving average. That is, a final seasonally adjusted estimate for a single time point requires up to 5 years of monthly data preceding and following that time point. For recent data, asymmetric filters, with less desirable properties than symmetric filters, must be used.
Beginning in December 2021, some seasonally adjusted CPS series are adjusted using the SEATS component of the X-13ARIMA-SEATS program rather than the X-11 component. Like the X-11 method, SEATS decomposes the observed series into trend (trend-cycle), seasonal, and irregular components and its relationship between the components may be additive or multiplicative (via a log transformation). Both the X-11 and SEATS methods use moving averages to decompose the series. The major difference between the two procedures is how the moving averages are constructed. The X-11 method by default selects from a set of predefined filters while the SEATS method derives its filters from a decomposition of the ARIMA model fit to the observed series into models for the trend, seasonal, and irregular components. The SEATS filters therefore are more tailored to the specific properties of the series as reflected in the ARIMA model fit while X-11 filters are nonparametric in that they can fit a wide variety of series without depending on a specific model.
A series should be seasonally adjusted if three conditions are satisfied: the series is seasonal, the seasonal effects can be estimated reliably, and no residual seasonality is left in the adjusted series. A variety of diagnostic tools are available for the X-11 method to test for these conditions, including frequency-spectrum estimates, revision-history statistics, and various seasonal tests. The X-13ARIMA-SEATS program provides some of the above diagnostics for SEATS analysis but also provides a battery of model-based diagnostics. If diagnostic testing shows that any of the three conditions listed fails to hold for a given series, that series is deemed not suitable for seasonal adjustment.
Concurrent seasonal adjustment of national CPS labor force data began at BLS with the release of estimates for December 2003 in January 2004. Prior to concurrent seasonal adjustment, BLS adjusted CPS data with the projected-factor method, which updated seasonal factors twice a year. Under this procedure, projected seasonal factors were used to seasonally adjust the new original data as they were collected. At midyear, the historical series were updated with data for January through June, and the seasonal adjustment program was rerun to produce projected seasonal factors for July through December of the current year.
With concurrent seasonal adjustment, the seasonal adjustment program is rerun each month as the latest CPS data become available. The seasonal factors for the most recent month are produced by applying a set of moving averages to the entire data set, extended by extrapolations, including data for the current month. While all previous-month seasonally adjusted estimates are recalculated in this process, BLS policy is to not revise previous months' official seasonally adjusted CPS estimates as new data become available during the year. Instead, revisions are introduced for the most recent 5 years of data at the end of each year. Numerous studies, including a 1987 paper11 on the CPS labor force series, have indicated that concurrent adjustment generally produces initial seasonally adjusted estimates requiring smaller revisions compared to estimates produced with the projected-factor method. Revisions to data for previous months also may produce gains in accuracy, especially when the original data are themselves regularly revised on a monthly basis. Publishing numerous revisions during the year, however, can confuse data users.
The case for revisions to previous-month seasonally adjusted estimates is less compelling for CPS series, because the original sample data normally are not revised. Moreover, an empirical investigation indicated that there were no substantial gains in estimating month-to-month changes by introducing revisions to the data for the previous month. For example, it was found that if previous-month revisions were made to the labor force series, the overall unemployment rate would be different in only 2 months between January 2001 and November 2002, in each case by only one-tenth of a percentage point.
BLS directly seasonally adjusts CPS series on the basis of age, sex, industry, education, and other characteristics. BLS also provides seasonally adjusted totals, subtotals, and ratios of selected series. It is possible to seasonally adjust an aggregate series either directly or indirectly by seasonally adjusting its components and adding the results, or dividing in the case of ratios. Indirect and direct adjustments usually will not give identical results, because
BLS uses indirect seasonal adjustment for most of the major labor force aggregates. Besides retaining, so far as possible, the essential accounting relationships, the indirect approach is needed because many of the aggregates include components with different seasonal and trend characteristics that sometimes require different modes of adjustment.
Examples of indirectly seasonally adjusted series are the levels of total unemployment, employment, and the civilian labor force, as well as the unemployment rate for all civilian workers. These series are produced by the aggregation of some or all of the seasonally adjusted series for the eight major civilian labor force components. The seasonally adjusted level of total unemployment is the sum of the seasonally adjusted levels of unemployment for four age-sex groups: men 16 to 19 years, women 16 to 19 years, men 20 years and over, and women 20 years and over. Likewise, seasonally adjusted civilian employment is the sum of the seasonally adjusted levels of employment for the same four age-sex groups. The seasonally adjusted civilian labor force is the sum of all eight components. The seasonally adjusted civilian unemployment rate is computed as the ratio of the total seasonally adjusted unemployment level to the total seasonally adjusted civilian labor force (expressed as a percentage).
A problem with producing seasonally adjusted estimates for a series by aggregation is that seasonal adjustment factors cannot be directly computed for that series. Implicit seasonal adjustment factors, however, can be calculated after the fact by taking the ratio of the unadjusted aggregate to the seasonally adjusted aggregate or, for additive implicit factors, the difference between those two aggregates.
Richard B. Tiller (retired, BLS) and Brian C. Monsell (retired, Census Bureau and BLS) contributed to a previous version of this article.
1 The X-11 method is described in Julius Shiskin, Allan Young, and John Musgrave, "The X-11 Variant of the Census Method II Seasonal Adjustment Program," Technical Paper no. 15 (Bureau of the Census, 1967). For documentation on X-11-ARIMA, see Estela Bee Dagum, The X-11 ARIMA Seasonal Adjustment Method, catalogue no. 12-564E (Ottawa, Statistics Canada, 1980) and Estella Bee Dagum, X11ARIMA Version 2000: Foundations and User’s Manual. For a detailed discussion of X-12-ARIMA, see David F. Findley, Brian C. Monsell, William R. Bell, Mark C. Otto, and Bor-Chung Chen, "New Capabilities and Methods of the X-12-ARIMA Seasonal Adjustment Program," Journal of Business and Economics Statistics, April 1998, pp. 127-152.
2 For documentation on X-13ARIMA-SEATS, see The X-13ARIMA-SEATS Reference Manual, (Washington, Bureau of the Census, April 2025).
3 For documentation on the SEATS program, which was developed by Victor Gomez and Agustin Maravall, see "Seasonal Adjustment and Signal Extraction in Economic Time Series," in D. Peña, G.C. Tiao, and R.S. Tsay (eds.), A Course in Time Series Analysis, Ch.8, 202-247, New York: J. Wiley and Sons, 2001. For more information on SEATS, see Seasonal Adjustment in Economic Time Series: The Experience of the Banco de España (With the Model Based Method) by Alberto Cabrero, Banco de España technical paper.
4 For a more detailed discussion of ARIMA models, refer to George E.P. Box and Gwilym M. Jenkins, Time Series Analysis: Forecasting and Control (San Francisco, Holden Day, 1970); and Sir Maurice Kendall and J. Keith Ord, Time Series (New York, University Press, 1990).
5 George E.P. Box and George C. Tiao, "Intervention Analysis with Applications to Economic and Environmental Problems," Journal of the American Statistical Association, vol. 70, no. 353, 1975, pp. 71-79.
6 For more details, see Section 4.1 of the X-13-ARIMA-SEATS Reference Manual, with special attention paid to equations 4.3 and 4.4.
7 Automatic outlier detection is based on the work of I. Chang, G.C. Tiao, and C. Chen, "Estimation of Time Series Parameters in the Presence of Outliers," Techonometrics, 1988, pp. 193-204. For more information on how this is implemented in X-13ARIMA-SEATS, see "New Capabilities and Methods of the X-12-ARIMA Seasonal Adjustment Program."
8 See "Revisions to the Current Population Survey Effective in January 2003."
9 For more details, see the seasonal adjustment methodology documentation published in January 2002.
10 For more information on how this is implemented in X-13ARIMA-SEATS, see "New Capabilities and Methods of the X-12-ARIMA Seasonal Adjustment Program." For extensive details on handling missing observations, see Victor Gomez, Agustin Maravall, and Daniel Pena, “Missing observations in ARIMA models skipping approach versus additive outlier approach,” Journal of Econometrics, v. 88, 1999, pp. 341-363.
11 See George R. Methee and Robert J. McIntire, "An Evaluation of Concurrent Seasonal Adjustment for the Major Labor Force Series," in Proceedings of the Business and Economic Statistics Section (Alexandria, VA, American Statistical Association, 1987).
Last Modified Date: January 14, 2026