Handbook of Methods > Industry Productivity Measures

Handbook of Methods Industry Productivity Measures Estimation

Industry Productivity Measures: Estimation

Productivity statistics describe how efficiently an industry produces goods and services. This is done is by separately calculating industry inputs and outputs. Change in the quantity of output that is not explained by an equivalent change in inputs is defined as growth (or decline) in productivity. The following section will describe the mathematical principles and techniques by which industry output, inputs, and productivity series are measured.

Output

Industry output is usually measured as a weighted index of the changes in the various products or services (in real terms) provided for sale outside the industry. Real output is most often derived by deflating nominal sales or values of production using BLS price indexes, but for a few industries it is measured by physical quantities of output. Each of these methods is explained below.

Deflated value output indexes are derived from data on the value of industry output adjusted for price change. The adjustment for price change is accomplished by dividing the nominal value of output by one or more price indexes. Nominal values of industry output are adjusted where possible to reflect the total value of industry output from both employer and nonemployer firms and to remove sales between establishments in the same industry, referred to as intraindustry transfers. Value of industry output is further adjusted by removing resales and accounting for changes in inventory. Revenues are deflated at the detailed product-class level to take into account changes in the mix of products over time. The deflated revenues for each output category are then aggregated together using the Törnqvist formula. The resulting real output indexes are conceptually equivalent to indexes that are developed using data derived from physical quantities of output.

Where possible, physical quantity output indexes are Törnqvist aggregations of the quantities of individual products. The basic data on quantities generally reflect primary products for each industry, at the most detailed level possible. Physical quantity output indexes are used for some industries within the mining, utilities, and transportation sectors, and at community hospitals, commercial banking, and postal services.

For an industry producing a single uniform product or service, the output index is simply the ratio of the number of units produced in the current year divided by the number of units produced in the base year. More typically, industries produce a number of different products or perform a number of different services. For these industries, output is calculated with a Törnqvist formula:

$\begin{array}{l} \frac{Q_{t}}{Q_{t - 1}} = exp [\sum_{i = 1}^{n} w_{i,t} (ln \frac{q_{i,t}}{q_{i,t - 1}})] \\ where \\ Q = the aggregate quantity of industry output, expressed as an annual index, \\ n = number of products, \\ q = quantity of product i in year t; upon which is computed the natural logarithm of the ratio \\ of quantity in the current year to that of the previous year, and \\ \begin{array}{l} w = the average value share weight for product i in time t. \\ The average value share weight for product i is computed as : \\ w_{i,t} = (s_{i,t} + s_{i,t - 1}) \div 2 \\ \begin{array}{l} where \\ s = the yearly share weight for product i in year t, which in turn is computed as: \\ s_{i,t} = p_{i,t} q_{i,t} \div (\sum_{i = 1}^{n} p_{i,t} q_{i,t}) \\ where \\ p = price of product i at time t. \end{array} \end{array} \end{array}$ formula

The Törnqvist formula yields the ratio of output in a given year to that in the previous year. The ratios arrived at in this manner then must be chained together to form a time series. If t = 3 and the base year is denoted by o, then

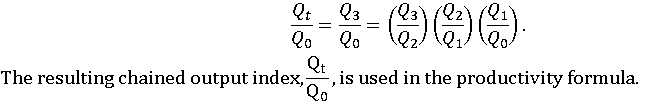
$\begin{array}{l} \frac{Q_{t}}{Q_{0}} = \frac{Q_{3}}{Q_{0}} = (\frac{Q_{3}}{Q_{2}}) (\frac{Q_{2}}{Q_{1}}) (\frac{Q_{1}}{Q_{0}}) . \\ The resulting chained output index, \frac{Q_{t}}{Q_{0}}, is used in the productivity formula. \end{array}$ formula

Hours worked

Total annual hours worked for each industry are estimated separately for three categories: paid employees, self-employed, and unpaid family workers. Average weekly hours of paid employees are collected by the BLS Current Employment Statistics (CES) on an hours-paid basis. This includes time when employees are on leave. Therefore, ratios of hours worked to hours paid from the National Compensation Survey are applied to the CES data. This results in the average weekly hours worked, which are multiplied by employment to calculate total annual hours worked. The annual hours of the three categories of workers are then aggregated to derive total industry hours worked. Hours worked of all persons at the industry level are treated as homogeneous, with no distinction made between the quality of hours worked by employees with different skill levels and education.

Labor productivity

To calculate a labor productivity index, an index of industry output is divided by an index of hours worked:

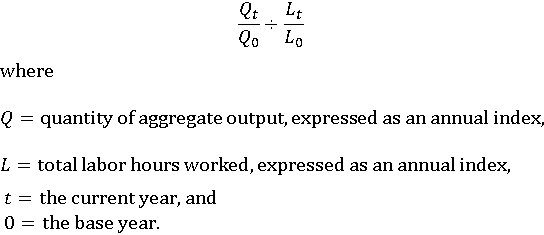
$\begin{array}{l} \frac{Q_{t}}{Q_{0}} \div \frac{L_{t}}{L_{0}} \\ where \\ Q = quantity of aggregate output, expressed as an annual index, \\ L = total labor hours worked, expressed as an annual index, \\ \begin{matrix} \begin{array}{l} t= the current year, and \\ 0= the base year. \end{array} \end{matrix} \end{array}$ formula

Unit labor costs

Indexes of unit labor costs are computed by dividing an index of industry labor compensation by an index of real industry output:

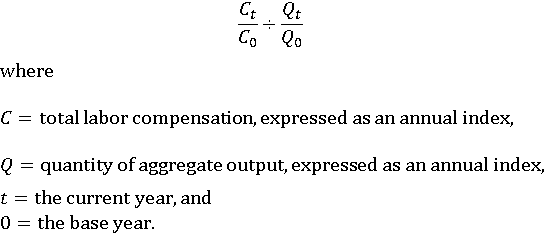
$\begin{array}{l} \frac{C_{t}}{C_{0}} \div \frac{Q_{t}}{Q_{0}} \\ where \\ C = total labor compensation, expressed as an annual index, \\ Q = quantity of aggregate output, expressed as an annual index, \\ \begin{matrix} \begin{array}{l} t = the current year, and \\ 0 = the base year. \end{array} \end{matrix} \end{array}$ formula

Capital services

Capital services are estimated by calculating productive capital stocks; capital services are assumed to be proportional to changes in the quantity of capital stocks for each asset. The capital index is a Törnqvist index of separate quantity indexes of equipment, structures, inventories, and land.

Capital stocks are composed of numerous different assets purchased at different times, including categories of equipment, structures, inventories, and land. The measure of capital stock for each year includes that year’s investment in an asset plus the remaining productive stock from all previous years’ investments. Capital stocks of equipment and structures for each industry are calculated using the perpetual inventory method, which takes into account the continual additions to and subtractions from the stock of capital as new investment and retirement of old capital occur. Real (constant dollar) investments in various assets are estimated by deflating current dollar investments with appropriate price deflators. The perpetual inventory method measures real stocks at the end of a year equal to a weighted sum of all past investments, where the weights are the asset’s efficiency relative to a new asset. A hyperbolic age efficiency function is used to calculate the relative efficiency of an asset at different ages.

The hyperbolic age-efficiency function can be expressed as

$\begin{array}{l} S_{t} = (L - t) / (L - (β) t) \\ where \\ \begin{array}{l} S_{t} = the relative efficiency of a t-year old asset, \\ L = the service life of the asset, \\ \begin{array}{l} t = the age of the asset, and \\ β = the parameter of efficiency decline. \end{array} \end{array} \end{array}$ formula

The service life of the asset for each cohort of each type of equipment and structure is assumed to be normally distributed around an average service life for that asset type. For most assets, these service lives are the same across all industries. The parameter of efficiency decline is assumed to be 0.5 for equipment and 0.75 for structures.^⁠1

These parameters yield a function in which assets lose efficiency more slowly at first, and then lose efficiency more rapidly later in their service lives.

Stocks are calculated for three separate categories of inventories: finished goods, work in process, and materials and supplies. Inventory stocks for each year are calculated as the average of the end-of-year stocks in years t and t-1 to represent the average on hand during the year as a whole. Current-dollar values of finished goods and work in process inventories are deflated with an implicit price deflator of each industry’s output. Current-dollar values of materials and supplies inventories are deflated with a weighted aggregation of PPIs matched to various amounts of materials consumed, specific to each industry.

Land stocks are estimated as a function of the change in constant-dollar structures stocks for each industry.

The various equipment, structure, inventory, and land stock series in constant dollars are aggregated into one capital input measure using a Törnqvist formula. Capital stocks multiplied by implicit rental prices yield cost share weights. Rental prices are calculated for each asset as

$\begin{array}{l} RP= [(P * R) + (P * D) - (∆p)] (1 - uz - k) / (1 - u) \\ where \\ RP = the rental price, \\ P = the deflator for the asset, \\ R = the internal rate of return, \\ D = the rate of depreciation for the asset, and \\ ∆p = the capital gain term representing the price change of the asset over the prior three years \\ (1-uz-k)/(1-u) reflects the effects of taxation where \\ u = the corporate tax rate, \\ z = the present value of $1 of deprecation deductions, and \\ k = the effective investment tax credit rate. 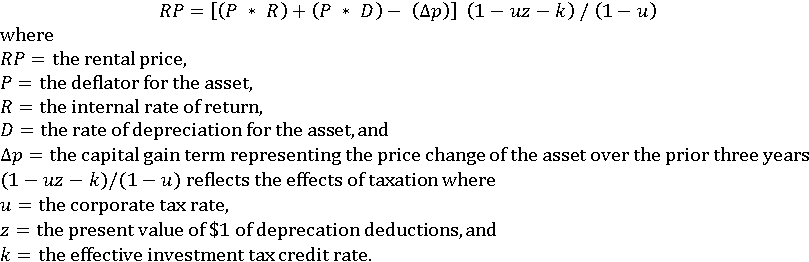\end{array}$ formula

Rental prices are expressed in rates per constant dollar of productive capital stocks. Each rental price is multiplied by its constant-dollar capital stock to obtain asset-specific capital costs, the shares of which are used for Törnqvist aggregation.

Intermediate purchases

The materials, purchased services, fuels, and electricity consumed by each industry are called intermediate purchases. Except for electricity consumed by manufacturing industries, for which direct quantity data are available, quantities are derived by deflating current-dollar values with appropriate price deflators.

Constant-dollar materials consumed are calculated by dividing annual current-dollar industry purchases by a weighted price deflator for each industry. Materials deflators are constructed for each industry by combining producer price indexes and import price indexes from BLS for detailed commodities. The deflators are combined using weights based on detailed commodity data from the Bureau of Economic Analysis (BEA) benchmark input-output tables. Price indexes to deflate purchased business services are constructed in a similar manner using CPIs, PPIs, or deflators developed by BEA. The value of fuels consumed by each industry is deflated with a weighted price deflator based on PPIs for individual fuel categories; the weights reflect fuel expenditures by industry from the Energy Information Administration (EIA), U.S. Department of Energy.

The separate indexes of real materials, services, fuels, and electricity are aggregated into a total intermediate purchases index using the Törnqvist formula. The weights for each component are derived by dividing the current dollar cost of each by the total combined cost of intermediate purchases, and averaging these weights at times t and t-1.

Combined Inputs

The annual growth rates of hours worked, capital services, and intermediate purchases are aggregated using their relative cost shares as weights. The cost of hours worked equals labor compensation. The weight for intermediate purchases is the sum total cost of materials, fuels, electricity, and purchased services. The cost of capital is derived as a residual, which is calculated as the value of sectoral production minus the costs of labor compensation and intermediate purchases.

The quantity indexes of hours worked, capital services, and intermediate purchases are combined using the Törnqvist formula to create an index of combined inputs.

Multifactor productivity

Multifactor productivity measures are derived by dividing an index of real industry output by an index of combined inputs of hours worked, capital services, and intermediate purchases.

$\begin{array}{l} ln (\frac{A_{t}}{A_{t - 1}}) = ln (\frac{Q_{t}}{Q_{t - 1}}) - [w_{k} (ln \frac{K_{t}}{K_{t - 1}}) + w_{l} (ln \frac{L_{t}}{L_{t - 1}}) + w_{ip} (ln \frac{{IP}_{t}}{{IP}_{t - 1}})] \\ where \\ \begin{array}{l} ln = the natural logarithm of the variable, \\ A = multifactor productivity, \\ \begin{array}{l} Q = output, \\ K = capital services, \\ \begin{array}{l} L = labor input (i.e. hours worked), \\ IP = intermediate purchases input, and \\ w_{k} w_{l} w_{ip} = cost share weights. 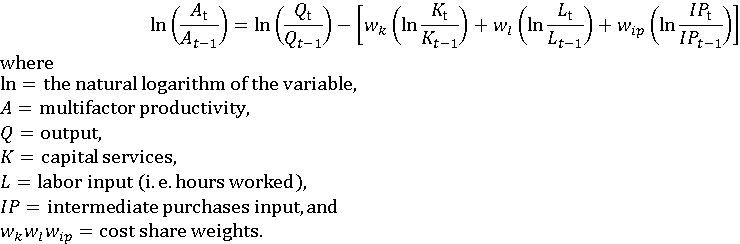\end{array} \end{array} \end{array} \end{array}$ formula

The input cost share weights are 2-year averages of the cost shares for each input (capital services, hours worked, and intermediate purchases), in years t and t-1, where

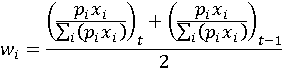
$w_{i} = \frac{{(\frac{p_{i} x_{i}}{\sum i (p_{i} x_{i})})}_{t} + {(\frac{p_{i} x_{i}}{\sum i (p_{i} x_{i})})}_{t - 1}}{2}$ formula

$p_{i} = price of input i (capital, hours worked, or intermediate purchases) in period t$

$x_{i} = quantity of input i in period t$

Since the growth rates are represented by differences in logarithms, the antilogs of the differences must be chained to form the index of multifactor productivity. A chain index is an index number in which the value of any given period is related to the value of its immediately preceding period; this is distinct from a fixed-base index, where the value of every period in a time series is directly related to the same value of one fixed base period.

Labor productivity is related to multifactor productivity in the manner given by the following formula:

$\ln (\frac{Q_{t}}{Q_{t - 1}}) - \ln (\frac{L_{t}}{L_{t - 1}}) = \ln (\frac{A_{t}}{A_{t - 1}}) + w_{k} [ln (\frac{K_{t}}{K_{t - 1}}) - \ln (\frac{L_{t}}{L_{t - 1}})] + w_{ip} [ln (\frac{{IP}_{t}}{{IP}_{t - 1}}) - \ln (\frac{L_{t}}{L_{t - 1}})]$ .

The equation above shows that the rate of change in labor productivity (on the left side of the equation) is equal to the change in multifactor productivity plus the effects of factor substitution; that is, the combined effects of changes in the weighted capital–labor ratio and the weighted intermediate purchases–labor ratio (which are represented on the right side of the equation). Conversely, the equation also shows that the change in multifactor productivity equals the change in labor productivity, adjusted to remove the weighted changes in capital and intermediate purchases relative to labor.

Limitations

Labor productivity and multifactor productivity measures are subject to certain limitations. First, existing techniques may not fully take into account changes in the quality of goods and services produced, which could result in reduced measures of output. Second, although efforts have been made to maintain consistency of coverage between the output and input estimates, some statistical differences may remain. For example, establishment lists might differ between surveys of industry revenue and surveys of hours. Third, estimates of outputs and inputs for detailed industries are subject to more volatility and error than estimates for more aggregate sectors. Finally, year-to-year changes in productivity are volatile and, therefore, are not necessarily indicative of changes in long-term trends. Conversely, long-term trends are not necessarily applicable to any one year or to any period in the future. Because of these and other statistical limitations, these indexes cannot be considered precise measures; instead, they should be interpreted as general indicators of movements of productivity.

Notes

^⁠1See “The Measurement of Capital by Charles R. Hulten, available at http://www.nber.org/chapters/c5974, page 25.

Last Modified Date: August 08, 2017