An official website of the United States government
 United States Department of Labor
United States Department of Labor
The Job Openings and Labor Turnover Survey (JOLTS) program uses the following methodologies to generate the estimates. The methodologies below are presented in terms of their order of operation.
Estimation of JOLTS estimates at the national level involves the following processes: unit nonresponse adjustment, item nonresponse adjustment, monthly benchmarking and estimation, automatic outlier detection, birth and death model estimation, estimates review and outlier selection, alignment, seasonal adjustment, and variance estimates. Establishment size class levels are also produced. These processes are described in detail below.
A multiplicative nonresponse adjustment factor (NRAF) is used to inflate the weight of respondents in an estimation cell to adjust for nonrespondents. The weight of all nonrespondents is redistributed among the respondents to preserve the total weighted employment of the cell. The NRAF is calculated by dividing the weighted frame employment of the viable establishments in the cell by the weighted frame employment of usable sample units in the cell:
![]()
where,
cell = the industry division, census region, and establishment size,
i = the ith establishment, viable designates those in-scope sampled units which are capable of reporting; that is, sampled units that are not out of business, out of scope, or duplicates, usable designates a subset of viable units, that is, those units which responded to the JOLTS with usable data,
empi = the sample frame employment of the ith unit, and
wi = the sampling weight of the ith unit.
Note: By definition, NRAF >= 1 since the number of usable units is less than or equal to the number of viable units.
Item nonresponse occurs when a respondent reports some of the JOLTS data elements, but not others. When a respondent only partially reports JOLTS data, the missing data must be replaced. The replacement of missing data mitigates bias, increases statistical efficiency, and increases the ease of data analysis. Imputation is the process by which missing values are replaced by an estimate based on other available data.
To impute data elements that have not been reported, the JOLTS program classifies establishments based on their employment dynamic—expanding, stable, or contracting—and imputes items within those groups. Thus, expanding establishments donate estimated item values to expanding establishments, stable to stable, and contracting to contracting. Drawing imputed values from a model-based donor distribution derived from reported data within a dynamic grouping reduces variation in the estimates. The imputation model also ensures that imputed data within dynamic groups are consistent with reported data within the corresponding groups without biasing the means of the data elements or substantially lowering their variances.
The imputation methodology produces three separate models for each of the JOLTS industry imputation cells. One model is based on the respondent rate distribution of stable establishments, a second is based on the respondent rate distribution of expanding establishments, and a third is based on the respondent rate distribution of contracting establishments. The employment dynamics classification is based on the reported over-the-month employment change of the respondents. The purpose of the models is to estimate vital characteristics of the entire distribution (mean, standard-deviation, skewness) based on full respondent data and then to impute missing values using a random draw from the estimated distribution.
Suppose that ![]() represents a variable of interest in JOLTS (job openings, hires, etc.) in industry id for a given month t. JOLTS item imputation is concerned only with those sampled establishments that reported at least employment. Complete nonrespondents are accounted for in JOLTS using a nonresponse adjustment factor (NRAF). Therefore, for each variable
represents a variable of interest in JOLTS (job openings, hires, etc.) in industry id for a given month t. JOLTS item imputation is concerned only with those sampled establishments that reported at least employment. Complete nonrespondents are accounted for in JOLTS using a nonresponse adjustment factor (NRAF). Therefore, for each variable![]() , respondent establishments can be classified as either item respondents
, respondent establishments can be classified as either item respondents![]() ) or as item nonrespondent
) or as item nonrespondent![]() ). Suppose that
). Suppose that ![]() represents reported employment for a JOLTS respondent within a given industry id and given month t and that
represents reported employment for a JOLTS respondent within a given industry id and given month t and that ![]() represents reported employment for the same JOLTS respondent within a given industry id and in the previous month. We can then define employments change as
represents reported employment for the same JOLTS respondent within a given industry id and in the previous month. We can then define employments change as ![]() .
.
The JOLTS imputation methodology subdivides the current industry imputation cell into three parts based on the reported employment change![]() for each respondent establishment.
for each respondent establishment.
where,
= 0 is the stable group with donor rates denoted as
> 0 is the expanding group with donor rates denoted as
< 0 is the contracting group with donor rates denoted as
where i=1,…,n given n donor establishments within the group for each industry.
A simple model of the item respondent rate distribution will then be constructed based on the known distribution characteristics of the item respondent rates for each group (![]() ). Independent draws from the model distribution will then be applied to the imputation recipient employment to produce imputed levels. The variables of interest within the actual reported donor data used to construct the model distribution are as follows:
). Independent draws from the model distribution will then be applied to the imputation recipient employment to produce imputed levels. The variables of interest within the actual reported donor data used to construct the model distribution are as follows:
1)The mean rate of the items within each group (![]() ), which is calculated as sum of the item over all-item respondents divided by the employment of all item respondents,
), which is calculated as sum of the item over all-item respondents divided by the employment of all item respondents, ![]()
2) The standard deviation of the absolute differences between item respondent rate and the cell mean within each group (![]() ), which is calculated as follows:
), which is calculated as follows:
ABS ( ![]() ), for each i in each id,group,ir cell.
), for each i in each id,group,ir cell.
3)The percentage of item respondents who report rates above the cell mean within each group (![]() )
)
It is important to note that the distribution of model rates is non-Normal. The distributions more resemble a skewed Uniform distribution, typically with the bulk of the distribution below the mean and with a thin long tail above the mean. Hence, the data from respondents is used to estimate the model attributes for each model (expanding, contracting, and stable) as the following illustration shows:
µ: The mean rate of the items within each group (![]() ).
).
![]() : The percentage of item respondents who report rates below the cell mean within each group (
: The percentage of item respondents who report rates below the cell mean within each group (![]() )
)
1- ![]() : The percentage of item respondents who report rates above the cell mean within each group (
: The percentage of item respondents who report rates above the cell mean within each group (![]() )
)
ψ: This variable is based on the observed standard deviation of the absolute value of the observed distance between reported rates and the cell mean and takes into account establishment size class. The value of ψ, in effect, determines the level of potential skewness for the model.
U(0, µ): Is a random uniform distribution of rates from 0 to µ.
U(µ, ψ): Is a random uniform distribution of rates from µ to ψ.
Imputed rate values are generated using two random draws from a Uniform distribution:
As the first step, a random draw from a U(0, 1) is made:
a. If the U(0, 1) is <= ![]() then a random draw from a U(0, µ) is made.
then a random draw from a U(0, µ) is made.
i. The imputed rate is equal to the random draw from a U(0, µ)
b. If the U(0, 1) is > ![]() then a random draw from a U(µ, ψ) is made.
then a random draw from a U(µ, ψ) is made.
i. The imputed rate is equal to the random draw from a U(µ, ψ)
Examples for contracting and expanding establishments
1. Example of the imputation method for contracting establishments i.e., those establishments for which employment declined over the month.
This example uses establishment data for a randomly chosen month (April 2011) for retail trade (id 44). We begin by sorting item respondents and item nonrespondents into their proper group based on their over-the-month employment change![]() .
.
We next summarize the set of item respondents with respect to the mean rate of the items within each group (![]() ), the standard deviation of the absolute differences between item respondent rate and the cell mean within each group (
), the standard deviation of the absolute differences between item respondent rate and the cell mean within each group (![]() ), and the percentage of item respondents who report rates above the cell mean within each group (
), and the percentage of item respondents who report rates above the cell mean within each group (![]() ). (See table 1, 2, and 3.)
). (See table 1, 2, and 3.)
| Data element | N | μ (mean) | Σ | ϐ |
|---|---|---|---|---|
|
Job openings |
133 | 3.99% | 5.43% | 76% |
|
Hires |
198 | 3.59 | 5.61 | 40 |
|
Quits |
174 | 2.4 | 3.98 | 59 |
|
Layoffs and discharges |
174 | 1.34 | 31.29 | 80 |
|
Other separations |
170 | 0.62 | 49.76 | 92 |
|
Source: U.S. Bureau of Labor Statistics. |
||||
| Data element | N | μ (mean) | Σ | ϐ |
|---|---|---|---|---|
|
Job openings |
173 | 4.70% | 3.05% | 85% |
|
Hires |
257 | 4.43 | 13.56 | 50 |
|
Quits |
218 | 1.61 | 2.07 | 84 |
|
Layoffs and discharges |
218 | 1.01 | 1.21 | 85 |
|
Other separations |
212 | 0.07 | 0.59 | 94 |
|
Source: U.S. Bureau of Labor Statistics. |
||||
| Data element | N | μ (mean) | Σ | ϐ |
|---|---|---|---|---|
|
Job openings |
327 | 1.22% | 3.05% | 94% |
|
Hires |
351 | 2.05 | 4.08 | 85 |
|
Quits |
342 | 1.42 | 3.54 | 85 |
|
Layoffs and discharges |
342 | 0.69 | 5.4 | 93 |
|
Other separations |
340 | 0.14 | 0.36 | 97 |
|
Source: U.S. Bureau of Labor Statistics. |
||||
Each dynamic group differs with respect to the relationship between the cell means of hires and total separations. The JOLTS variable total separations represent the summation of its components of quits, layoffs and discharges, and other separations. If total separations are reported and any component of total separations is not, then the imputed components levels will be prorated to the reported total separations level.
In the contracting group, the mean hires rate (3.59 percent) is less than the sum of the total separations component means (4.36 percent). (See table 1.) The expanding group has a mean hires rate (4.43 percent) greater than the sum of the separations component means (2.68 percent), while the mean hires rate of stable establishments (2.05 percent) is approximately equal to the sum of the separations component means (2.25 percent). (See table 2 and 3.)
Next, in step 2, we construct the length of the proposed model distribution (![]() ) using the observed deviations (σ). The length (ψ) is equal to the value 1.645x(σ). (See tables 1A, 2A, and AC.)
) using the observed deviations (σ). The length (ψ) is equal to the value 1.645x(σ). (See tables 1A, 2A, and AC.)
| Data element | N | μ | σ (observed deviations) | Ψ(length) | β |
|---|---|---|---|---|---|
|
Job openings |
133 | 3.99% | 5.43% | 8.93% | 76% |
|
Hires |
198 | 3.59 | 5.61 | 9.23 | 40 |
|
Quits |
174 | 2.4 | 3.98 | 8.37 | 59 |
|
Layoffs and discharges |
174 | 1.34 | 31.29 | 51.89 | 80 |
|
Other separations |
170 | 0.62 | 49.76 | 81.86 | 92 |
|
Source: U.S. Bureau of Labor Statistics. |
|||||
| Data element | N | μ | σ | ψ | β |
|---|---|---|---|---|---|
|
Job openings |
173 | 4.70% | 3.05% | 5.01% | 85% |
|
Hires |
257 | 4.43 | 13.56 | 22.3 | 50 |
|
Quits |
218 | 1.61 | 2.07 | 3.41 | 84 |
|
Layoffs and discharges |
218 | 1.01 | 1.21 | 1.99 | 85 |
|
Other separations |
212 | 0.07 | 0.59 | 0.97 | 94 |
|
Source: U.S. Bureau of Labor Statistics. |
|||||
| Data element | N | μ | σ | ψ | β |
|---|---|---|---|---|---|
|
Job openings |
327 | 1.22% | 3.05% | 5.02% | 94% |
|
Hires |
351 | 2.05 | 4.08 | 6.71 | 85 |
|
Quits |
342 | 1.42 | 3.54 | 5.83 | 85 |
|
Layoffs and discharges |
342 | 0.69 | 5.4 | 8.88 | 93 |
|
Other separations |
340 | 0.14 | 0.36 | 0.97 | 97 |
|
Source: U.S. Bureau of Labor Statistics. |
|||||
Finally, in step 3, we construct the two uniform distributions from which imputed rates can be drawn. (See tables 1B, 2B, and 3B.) With probability β (the probability that an item respondent within the group has reported less than the cell mean) we will draw from U(0, ![]() , and with probability 1-β (the probability that an item respondents within the group has reported greater than the cell mean) we will draw from U(
, and with probability 1-β (the probability that an item respondents within the group has reported greater than the cell mean) we will draw from U(![]() .
.
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Job openings |
3.99% | 8.93% | 76% | U(0, 3.99%) | 24% | U(3.99%, 8.93%) |
|
Hires |
3.59 | 9.23 | 40 | U(0, 3.59) | 30 | U(3.59, 9.23) |
|
Quits |
2.4 | 8.37 | 59 | U(0, 3.98) | 41 | U(3.98, 8.37) |
|
Layoffs and discharges |
1.34 | 51.89 | 80 | U(0, 1.34) | 20 | U(1.34, 51.89) |
|
Other separations |
0.62 | 81.86 | 92 | U(0, 0.62) | 8 | U(0.62, 81.86) |
|
Source: U.S. Bureau of Labor Statistics. |
||||||
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Job openings |
4.70% | 5.01% | 85% | U(0, 4.70%) | 15% | U(4.70%, 5.01%) |
|
Hires |
4.43 | 22.3 | 50 | U(0, 4.43) | 50 | U(4.43, 22.30) |
|
Quits |
1.61 | 3.41 | 84 | U(0, 1.61) | 36 | U(1.61, 3.41) |
|
Layoffs and discharges |
1.01 | 1.99 | 85 | U(0, 1.01) | 15 | U(1.01, 1.99) |
|
Other separations |
0.07 | 0.97 | 94 | U(0, 0.07) | 6 | U(0.07, 0.97) |
|
Source: U.S. Bureau of Labor Statistics. |
||||||
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Job openings |
1.22% | 5.02% | 94% | U(0, 1.22%) | 6% | U(1.22%, 5.02%) |
|
Hires |
2.05 | 6.71 | 85 | U(0, 2.05) | 15 | U(2.05, 8.16) |
|
Quits |
1.42 | 5.83 | 85 | U(0, 1.42) | 15 | U(1.42 ,5.83) |
|
Layoffs and discharges |
0.69 | 8.88 | 93 | U(0, 0.69) | 7 | U(0.69, 8.88) |
|
Other separations |
0.14 | 0.97 | 97 | U(0, 0.14) | 3 | U(0.14, 0.59) |
|
Source: U.S. Bureau of Labor Statistics. |
||||||
The final data required to produce imputed rates are the lengths of the six size class distributions (![]() for each variable. These lengths are calculated the same way as the group lengths; however, these lengths are based on the data across all industries and groups for a given month. The following matrix details the size class lengths (size x variable matrix). (See table 4.)
for each variable. These lengths are calculated the same way as the group lengths; however, these lengths are based on the data across all industries and groups for a given month. The following matrix details the size class lengths (size x variable matrix). (See table 4.)
| ψ = Observed standard deviations | |||||
|---|---|---|---|---|---|
|
Size class |
Job openings | Hires | Quits | Layoffs and discharges | Other separations |
|
1 |
72.60% | 28.11% | 10.42% | 28.52% | 61.01% |
|
2 |
38.07 | 27.4 | 5.9 | 26.05 | 2.58 |
|
3 |
24.15 | 11.45 | 3.04 | 10.5 | 0.56 |
|
4 |
15.54 | 9.38 | 2.3 | 21.17 | 0.55 |
|
5 |
5.01 | 7.11 | 2.54 | 4.41 | 0.39 |
|
6 |
2.43 | 1.63 | 0.72 | 1.27 | 0.37 |
We can now begin imputing rates. In this example, the retail trade establishment has a reported employment of 2,648 employees (classifying it as size class 5), and its over-the-month employment change is negative 3. It is therefore classified as a contracting establishment. The truncated table 1B below will then be used to impute job openings for this nonrespondent.
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Job openings |
3.99% | 8.93% | 76% | U(0, 3.99%) | 24% | U(3.99%, 8.93%) |
In the ![]() matrix above, we note that the job opening length (
matrix above, we note that the job opening length (![]() ) for size class 5 is 5.01 percent. (See table 4.) Since the value of
) for size class 5 is 5.01 percent. (See table 4.) Since the value of![]() is 8.93 percent for the retail trade contracting group (id 44) is greater than the size class 5 job openings length (5.01 percent), we replace the upper bound value for the id/group with the
is 8.93 percent for the retail trade contracting group (id 44) is greater than the size class 5 job openings length (5.01 percent), we replace the upper bound value for the id/group with the ![]() value of the size. The table 1C illustrates this adjustment:
value of the size. The table 1C illustrates this adjustment:
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Job openings |
3.99% | 5.01% | 76% | U(0, 3.99%) | 24% | U(3.99%, 5.01%) |
We begin item imputation by drawing from a standard uniform distribution, U(0, 1), to determine if the imputed rate is to be drawn from the “below” uniform distribution or the “above” uniform distribution. If the value of the U(0, 1) is less than β then we will draw from the “below” uniform distribution, otherwise we will draw from the “above” distribution.
If U(0,1) <= β, then draw from U(0, 3.99%)
If U(0,1) > β, then draw from U(3.99%, 5.01%)
Suppose that the value drawn from U(0, 1) is 0.1616, then since 16 percent is lower than 76 percent, we will draw from the “below” distribution, U(0, 0.0399). Suppose that the random value drawn from the U(0, 0.0399) distribution is 0.02854. The imputed rate for job openings for this establishment is 0.02854, while the imputed level is the reported employment of the establishment being imputed multiplied by the imputed rate (2,648 x 0.02854) so the imputed job openings level is 75.57.
2. Example of the imputation method for expanding establishments i.e., those establishments for which employment increased over the month.
In the second example, the establishment is an item nonrespondent for quits. The reported employment is 111 employees (classifying it as size class 3), and its over-the-month employment change is positive 1. It is therefore classified as an expanding establishment. The truncated table 2B will then be used to impute quits for this nonrespondent.
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Quits |
1.61% | 3.41% | 64% | U(0, 1.61%) | 36% | U(1.61%, 3.41%) |
In the ![]() matrix, we note that the quits length (
matrix, we note that the quits length (![]() ) for size class 3 is 0.0304. Since the quits value of
) for size class 3 is 0.0304. Since the quits value of![]() for the retail trade expanding establishments group is 0.0341 and greater than the size class 3 quits length of 0.0304 (from table 4), we replace the upper bound value for the id/group with the
for the retail trade expanding establishments group is 0.0341 and greater than the size class 3 quits length of 0.0304 (from table 4), we replace the upper bound value for the id/group with the ![]() value of that size. Table 2C illustrates this adjustment:
value of that size. Table 2C illustrates this adjustment:
| Data element | μ | ψ | β | Below | (1-β) | Above |
|---|---|---|---|---|---|---|
|
Quits |
1.61% | 3.04% | 64% | U(0, 1.61%) | 36% | U(1.61%, 3.04%) |
As before, we begin item imputation by drawing from a standard uniform distribution, U(0, 1), to determine if the imputed rate is to be drawn from the “below” uniform distribution or the “above” uniform distribution. If the value of the U(0, 1) is less than β then we will draw from the “below” uniform distribution, otherwise we will draw from the “above” distribution.
If U(0,1) <= β then draw from U(0,1.61%)
If U(0,1) > β then draw from U(1.61%,3.04%)
Suppose that the value drawn from U(0,1) is 0.9876, then since 0.9876 is greater than 0.64, we will draw from the “above” distribution, U(0.0161, 0.0304). Suppose that the random value drawn from U(0.0161, 0.0304) distribution is 0.01705. The imputed rate for quits for this establishments thus 0.01705, while the imputed level is the reported employment of the establishment being imputed multiplied by the imputed rate, 111 x 0.01705, so the imputed quits level is 1.89.
JOLTS weighted employment for each estimation cell is adjusted through a process called benchmarking. JOLTS estimation cells are benchmarked monthly to the current employment level from the U.S. Bureau of Labor Statistics (BLS) Current Employment Statistics (CES) program. The resulting factor is the benchmark factor (BMF). In addition, the weights are adjusted to account for aggregation and disaggregation of establishments. The sampled weight is adjusted to ensure that JOLTS weighted employment is equal to CES employment.
JOLTS estimates are calculated by multiplying the establishment weight, the estimation cell nonresponse adjustment factor (NRAF), the estimation cell BMF, and any necessary aggregation adjustment. The product is summed across the estimation cell to produce the estimate for that cell.
A Horvitz–Thompson estimator with a ratio adjustment is used to produce estimates of levels of the surveyed data elements at different degrees of geographical and industrial detail. To calculate the estimated level for each data element for a given month in a basic estimation cell, the following steps are performed:
To ratio-adjust JOLTS employment to CES employment, it is necessary to calculate the summed weighted total employment (SWTE) for each JOLTS industry division within a census region (region/id).
The final weighted JOLTS employment for each record in a region/id cell is calculated by multiplying the following: sample weight x NRAF x reported JOLTS employment for that record.
The SWTE is calculated in each region/id cell by summing the final weighted JOLTS employment in each region/id cell.
The BMF is calculated by dividing CES employment (at the region/id level) by the SWTE (at the region/id level).
The CES program produces an industry employment estimate using a much larger sample than JOLTS.
Ratio adjusting JOLTS data element estimates to CES industry employment increases the statistical reliability of all JOLTS data element estimates.
![]()
where,
id,cr = industry division and census region,
BMFid,cr = the benchmark factor for industry and census region,
CESid,cr = industry division and census region employment,
wi = the sampling weight reflecting all adjustments (NRAF, atypical data adjustment, etc.) for sample unit i, and
ei = reported employment from sample unit i.
Thus, the equation used to compute the estimate of a characteristic is
![]()
where weight is the recomputed (i.e. reweight) sampling weight.
Each data element—job openings, hires, and separation type—is estimated this way. The resulting levels are converted to rates. The hires and separations rates are computed by dividing the number of separations by employment and multiplying that quotient by 100. The job openings rate is computed by dividing the number of job openings by the sum of employment and job openings and multiplying that quotient by 100.
Winsorization is a statistical process commonly used to reset outlier values to a predetermined threshold value, also called the cutoff value. In JOLTS, an independent cutoff value is established for each employment size and data element (job openings, hires, etc.). Any reported value exceeding the cutoff is reset to the cutoff value.
As with any sample survey, the JOLTS sample can only be as current as its sampling frame. The time lag from the birth of an establishment until its appearance in the sampling frame is approximately 1 year. In addition, many new establishments fail within the first year. Because new and short-lived universe establishments cannot be reflected in the sampling frame immediately, the JOLTS sample cannot capture job openings, hires, and separations from these establishments during their early existence. BLS has developed a model for estimating birth and death activity in current months by examining data on birth and death activity in previous years as collected by the Quarterly Census of Employment and Wages (QCEW) and projecting forward to the present using over-the-year change in the CES. The birth-death model also uses historical JOLTS data to calculate the amount of churn (meaning the rates of hires and separations) that exists in establishments of various sizes. The model then combines the calculated churn with the projected employment change to estimate the number of hires and separations that take place in these establishments that cannot be measured through sampling.
The model-based estimate of total separations is distributed to the three components of total separations—quits, layoffs and discharges, and other separations—in proportion to their contribution to the sample-based estimate of total separations. In addition, job openings in the establishments modeled are estimated by computing the ratio of openings to hires in the collected data and applying that ratio to the modeled hires. The estimates of job openings, hires, and separations produced by the birth-death model are then added to the sample-based estimates produced from the survey to arrive at the estimates for job openings, hires, and separations.
During monthly estimates review and annual processing, JOLTS staff conduct a manual review for not seasonally adjusted estimates containing potential outliers. Estimates are examined for atypical or large movements. Those estimates that need investigation are flagged. To investigate a flagged estimate, JOLTS staff examine the microdata by establishment that contributed to that estimate. If microdata for a reporting establishment is confirmed atypical, the establishment is flagged as an outlier.
After estimates review, the not seasonally adjusted estimates are re-run and again reviewed.
Conceptually, the JOLTS estimates of hires minus separations should be comparable to the CES over-the-month net employment change. The CES series is considered a highly accurate measure of net employment change due to its large sample and annual benchmark to universe counts of employment from the QCEW program. However, definitional differences combined with sampling and nonsampling errors between the two surveys have caused JOLTS to diverge from the CES survey over time. To limit the divergence and to improve the quality of the JOLTS hires and separations series, BLS implemented a monthly alignment method. Simply put, there are four steps to this method: seasonally adjust, align, back out the seasonal adjustment factors, and re-seasonally adjust.
The monthly alignment method applies the seasonally adjusted CES employment trend to the seasonally adjusted JOLTS implied employment trend (hires minus separations), keeping the two trends consistent while preserving the seasonality of the JOLTS data. First, the two series are seasonally adjusted and the difference between the JOLTS implied employment trend and the CES net employment change is calculated. Next, the JOLTS implied employment trend is updated to equal the CES net employment change through a proportional adjustment. This proportional adjustment procedure modifies the two components (hires and separations) in proportion to their contribution to the total churn (hires plus separations). For example, if the hires estimate makes up 40 percent of the churn for a given month, it will receive 40 percent, and separations will receive 60 percent, of the needed adjustment.
The following is an example of the alignment method.
Let Hires denote the number of hires.
Let Seps denote the number of separations.
Let Cesemp represent CES employment.
Hires_sa = 40
Seps_sa = 60
D Cesemp = –25
In this case, hires minus separations does not equal the change in CES employment.
Then,
![]()
![]()
where D denotes the divergence between CES employment trend and JOLTS hires minus separations.
Let PAHires_sa denote the proportionally adjusted seasonally adjusted hires.
Let PASeps_sa denote the proportionally adjusted seasonally adjusted separations.
Let Hires_A denote aligned hires.
Let Seps_A denote aligned separations.
Then,
![]()
![]()
And,
![]()
![]()
Finally,
![]()
![]()
This yields the following:
Seasonally adjusted hires minus seasonally adjusted separations is equal to the change in CES employment.
Resulting in,
![]()
![]()
Job openings are aligned based on the ratio of job openings to hires from the not seasonally adjusted estimates. This ratio of job openings to hires is applied to the updated hires to compute the updated job openings. The adjusted job openings, hires, and separations are converted back to not seasonally adjusted data by reversing the application of the original seasonal adjustment factors.
Example:
Let JO denote job openings.
Let JO_A denote aligned job openings.
JO=11
To obtain aligned job openings,
![]()
![]()
The monthly alignment procedure assures a close match of the JOLTS implied employment trend with the CES employment trend for the not seasonally adjusted data. The aligned not seasonally adjusted estimates are then published.
After alignment, the seasonal adjustment program (X-13-ARIMA-SEATS) is used to seasonally adjust the JOLTS series. Seasonal adjustment is the process of estimating and removing periodic fluctuations caused by events such as weather, holidays, and the beginning and ending of the school year. Seasonal adjustment makes it easier to observe fundamental changes in data series, particularly those associated with general economic expansions and contractions. Each month, a concurrent seasonal adjustment methodology uses all relevant data, up to and including the data for the current month, to calculate new seasonal adjustment factors.
Moving averages are used as seasonal filters in seasonal adjustment. JOLTS seasonal adjustment includes both additive and multiplicative models, as well as regression with autocorrelated errors (REGARIMA) modeling, to improve the seasonal adjustment factors at the beginning and end of the series and to detect and adjust for outliers in the series.
The estimation of sample variance for the JOLTS survey is accomplished by using the balanced half samples (BHS) method. This replication technique uses half samples of the original sample to calculate estimates. The sample variance is calculated by measuring the variability of the subsample estimates. The sample units in each cell—where a cell is based on region, industry, and size class—are divided into two random groups. The basic BHS method is applied to both groups. The cells are subdivided systematically, in the same order as the initial sample selection. Weights for units in the half sample are multiplied by a factor of 1 + α , whereas weights for units not in the half sample are multiplied by a factor of 1 − α , where
![]()
in which γ is Fay’s factor (0.5). Fay’s method is a generalized form of BHS which uses the full sample but with unequal weights for each half sample. Sample weights are adjusted by ![]() in the formula above by setting y=0.5 for those units outside the half-sample and are adjusted by
in the formula above by setting y=0.5 for those units outside the half-sample and are adjusted by![]() by setting y=1.5 for those units within the half-sample.
by setting y=1.5 for those units within the half-sample.
The finite population correction (f) factor is calculated as
![]()
where,
rt,h = the number of units reporting employment in allocation stratum h at time t,
nh = the number of sample units in allocation stratum h, and
wiSEL = the sample selection weight of sample unit i.
The JOLTS estimates are revised annually to reflect annual updates to the CES employment estimates and incorporate new seasonal adjustment factors. The JOLTS employment levels (not published) are ratio-adjusted to the CES employment levels, and the resulting ratios are applied to all JOLTS data elements. This annual benchmarking process results in revisions to both the seasonally adjusted and not seasonally adjusted JOLTS series, for the period since the last benchmark was established. The seasonally adjusted estimates are recalculated for the most-recent 5 years to reflect updated seasonal adjustment factors. Further, the alignment methodology creates a dependency of the not seasonally adjusted estimates on the seasonal adjustment process. Therefore, the data series that are not seasonally adjusted are also recalculated for the most-recent 5 years to reflect the effect of the updated seasonal adjustment factors on the alignment process.
The JOLTS program produces estimates for job openings, hires, and separations by establishment size class. These estimates can help to better explain some of the internal dynamics of the labor market. The size class series are available back to December 2000. The estimates provide users with job openings, hires, and total separations, as well as the components of total separations: quits (voluntary separations), layoffs and discharges (involuntary separations), and other separations. (See size class definitions in the Concepts section.)
Size classes are estimated at the total private industry level. The estimation process for size class estimates uses the same processes that generate national estimates for industry and region, with two differences:
The JOLTS program produces estimates for all 50 states and the District of Columbia at the total nonfarm level for job openings, hires, and separations. The JOLTS sample of about 21,000 establishments does not directly support the production of sample-based state estimates. However, state estimates have been produced using other BLS program data by combining the available sample with model-based estimates.
These estimates consist of four major estimating models: the Composite Regional model (an unpublished intermediate model), the Synthetic model (an unpublished intermediate model), the Composite Synthetic model (published historical series through the most current benchmark year), and the Extended Composite Synthetic model (published current-year monthly series). The Composite Regional model uses JOLTS microdata, JOLTS regional published estimates, and CES employment data. The Composite Synthetic model uses JOLTS microdata and Synthetic model estimates derived from monthly employment changes in microdata from the QCEW, and JOLTS published regional data. The Extended Composite Synthetic extends the Composite Synthetic estimates by ratio-adjusting the Composite Synthetic by the ratio of the current Composite Regional model estimate to the Composite Regional model estimate from the previous year.
The Extended Composite Synthetic model (and its major component—the Composite Regional model) is used to extend the Composite Synthetic estimates because all of the inputs required by this model are available at the time monthly estimates are produced. In contrast, the Composite Synthetic model (and its major component—the Synthetic model) can only be produced when the latest QCEW data are available. The Extended Composite Synthetic model estimates are used to extend the Composite Synthetic model estimates during the annual JOLTS re-tabulation process. The extension of the Composite Synthetic model using current data-based Composite Regional model estimates will ensure that the Composite Synthetic model estimates reflect current economic trends.
The Composite Regional approach calculates state-level JOLTS estimates from JOLTS microdata using sample weights, and the adjustments for nonresponse (NRAF). The Composite Regional estimate is then benchmarked to CES state-supersector employment to produce state-supersector estimates. The JOLTS sample, by itself, cannot ensure a reasonably sized sample for each state-supersector cell. The small JOLTS sample results in several state-supersector cells that lack enough data to produce a reliable estimate. To overcome this issue, the state-level estimates derived directly from the JOLTS sample are augmented using JOLTS regional estimates when the number of respondents is low (that is, less than 30). This approach is known as a composite estimate, which leverages the small JOLTS sample to the greatest extent possible and supplements that with a model-based estimate. Previous research has found that regional industry estimates are a good proxy at finer levels of geographical detail. That is, one can make a reliable prediction of JOLTS estimates at the regional-level using only national industry-level JOLTS rates. The assumption in this approach is that one can make a good prediction of JOLTS estimates at the state-level using only regional industry-level JOLTS rates.
In this approach, the JOLTS microdata-based estimate is used, without model augmentation, in all state-supersector cells that have 30 or more respondents. The JOLTS regional estimate will be used, without a sample-based component, in all state-supersector cells that have fewer than five respondents. In all state-supersector cells with 5 to 30 respondents an estimate is calculated that is a composition of a weighted estimate of the microdata-based estimate and a weighted estimate of the JOLTS regional estimate. The weight assigned to the JOLTS data in those cells is proportional the number of JOLTS respondents in the cell (weight = n∕30, where n is the number of respondents).
The following are the inputs into the Composite model:
1. All JOLTS microdata are weighted using final weights. A weighted estimate is made for each JOLTS respondent.
2. Counts are made for each state-supersector cell.
3. Each JOLTS respondent is paired with its regional rate estimate for all variables.
4. Based on the count of respondents in the state-supersector cell the JOLTS respondent belongs to, a composite model weight (CMW) is calculated.
4.1. If the count is>30, then the CMW for the respondent data=1. The CMW for the regional estimate=0.
4.2. If the count<5, then the CMW for the respondent data=0. The CMW for the regional estimate=1.
4.3. If the count is 5–30, then the CMW for the respondent data = n∕30, where n is the number of respondents. The CMW for the regional estimate = (30−n)∕30.
5. The state-level rate estimate is therefore the final weighted respondent-based JOLTS rate times the CMW added to the regional rate times the CMW, benchmarked to CES state-level estimate:
5.1. FINAL ESTIMATE=CES STATE EMP×((final weight JOLTS rate×CMW)+(regional rate×CMW))
5.2. The Composite Regional supersector estimates are summed across state industry supersectors to the nonfarm level.
6. To stabilize the estimate, the sum of state Composite Regional estimates within each region is then benchmarked to the published JOLTS regional estimates.
This model produces state-level estimates of job openings, hires, quits, layoffs and discharges, and total separations. These estimates provide estimates for the most current month of estimates and can be produced during monthly JOLTS estimation production.
JOLTS data are somewhat volatile at the national and regional levels due to the small sample size which in turn results in volatile state estimates.
The Composite Regional estimates can vary substantially from Composite Synthetic estimates for states that exhibit seasonal employment patterns that differ substantially from the JOLTS region to which they belong. For example, Alaska has a pronounced seasonal employment pattern that differs from the West region in which it resides. Consequently, the Composite Regional estimates derived using West region JOLTS rates substantially understate the JOLTS rates in that state.
These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which are updated annually in June.
The Synthetic model differs fundamentally from the Composite Regional model. The Synthetic approach does not use JOLTS microdata but rather it uses data from the QCEW that have been linked longitudinally (Longitudinal Database—LDB), the QCEW–LDB. The Synthetic model attempts to convert QCEW–LDB monthly employment change microdata into JOLTS job openings, hires, quits, layoffs and discharges, and total separations data.
The following are inputs into the Synthetic model:
1. Every record on the QCEW-LDB is classified as expanding, contracting, or stable based on monthly employment change.
1.1. For expanding records, the amount of employment growth is converted to JOLTS hires. They are given no separations.
1.2. For contracting records, the amount of employment decline is converted to JOLTS separations. They are given no hires.
1.3. For stable records, no attribution of JOLTS hires or separations is made.
2. The entire QCEW-LDB is summarized to the U.S. Census regional level.
3. The QCEW-LDB regional summary is ratio adjusted to the JOLTS published regional estimate for hires and total separations.
3.1. For each region, the ratio of QCEW-LDB based regional hires and total separations to JOLTS published hires and total separations is calculated (Ratio-H for hires and Ratio-TS for total separations).
3.2. Each record on the QCEW-LDB within each U.S. Census region will have their converted JOLTS data multiplied by Ratio-H and Ratio-TS, by region.
3.2.1. For expanding records, the amount of employment growth is then: (JOLTS hires×Ratio-H). They remain with no separations.
3.2.2. For contracting records, the amount of employment decline is then: (JOLTS separations×Ratio-TS). They remain with no hires.
3.2.3. For stable records, they remain with no JOLTS hires or separations.
4. To produce state-level estimates, sum the regional hires×Ratio-H by state to produce a state-level JOLTS hires estimate and sum the TS×Ratio-TS by state to produce a state-level JOLTS total separations estimate.
State-level JOLTS estimates for hires and total separations come directly from the model outlined above. Synthetic job openings (![]() are a function of the ratio of industry-regional job openings and hires
are a function of the ratio of industry-regional job openings and hires ![]() . This ratio of published job openings to hires is applied to model hires estimates
. This ratio of published job openings to hires is applied to model hires estimates ![]() to derive model job opening estimates. Ratio-adjusting the JOLTS model hires and separations to the regional published JOLTS hires and separations estimates ensures that the JOLTS published churn rate is fully accounted for.
to derive model job opening estimates. Ratio-adjusting the JOLTS model hires and separations to the regional published JOLTS hires and separations estimates ensures that the JOLTS published churn rate is fully accounted for.
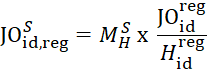
Synthetic quits and layoffs and discharges are a function of the relative percentage of the individual components of total separations at the industry-regional level ![]() . The relative percentages of each component are applied to the model separations estimates
. The relative percentages of each component are applied to the model separations estimates ![]() ) to derive model quits and layoffs and discharges
) to derive model quits and layoffs and discharges ![]() .
.
![]() ) to derive model quits and layoffs and discharges
) to derive model quits and layoffs and discharges ![]() .
.
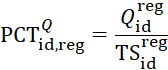
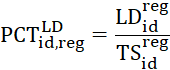
![]()
This approach is not meant to model individual QCEW-LDB data records. It would not be prudent to use this approach to model small populations (30 or fewer establishments). The model works best at the state-level. And while it is possible to model smaller populations, there potentially is a reduction in the strength of the model proportionate to the reduction in the size of the population being modeled.
The model does generate state-level job openings and separations breakouts. However, these estimates are based upon ratios that are common across the region to which a state belongs. If there are significant differences in the ratio of job openings to hires or separations breakouts for any particular state (or set of states) within a region, the model cannot detect that and estimates will not reflect those differences.
Since the model is based on QCEW-LDB data, the model cannot produce current state-level estimate since QCEW-LDB data lags current JOLTS estimation production by 6–9 months.
Composite Synthetic model
The Composite Synthetic model is nearly identical to the Composite Regional model. The primary difference is the use of the Synthetic model estimates (described in the composite regional model) rather than JOLTS published regional estimates when there is an insufficient amount of JOLTS microdata to produce a state-supersector estimate.
Like the Composite Regional approach, the JOLTS microdata-based estimate is used in all state-supersector cells that have 30 or more respondents. However, in contrast to the Composite Regional approach, the Composite Synthetic approach uses the Synthetic estimate in all state-supersector cells that have fewer than five respondents. In all state-supersector cells with 5–30 respondents, an estimate is calculated that is a composition of a weighted estimate of the microdata-based estimate and a weighted estimate of the Synthetic estimate. The weight assigned to the JOLTS data in those cells is proportional the number of JOLTS respondents in the cell (weight=n∕30, where n is the number of respondents).
The Composite Synthetic supersector estimates are summed across state-supersectors to the nonfarm level.
Composite Synthetic model inputs
The following are inputs into the Composite Synthetic model:
1. All JOLTS microdata are weighted using final weights. A weighted estimate is made for each JOLTS respondent.
2. Counts are made for each state-supersector cell.
3. Each JOLTS respondent is paired with its Synthetic model rate estimate for all variables.
4. Based on the count of respondents in the state-supersector cell the JOLTS respondent belongs to, a composite model weighted (CMW) estimate is calculated.
4.1. If the count is>30, then the CMW for the respondent data=1. The CMW for the Synthetic estimate=0.
4.2. If the count<5, then the CMW for the respondent data=0. The CMW for the Synthetic estimate=1.
4.3. If the count is 5–30, then the CMW for the respondent data=n∕30, where n is the number of respondents. The CMW for the Synthetic estimate=1−n∕30.
5. The state-level rate estimate is therefore the final weighted respondent-based JOLTS rate times the CMW added to the Synthetic model rate times the CMW, benchmarked to CES state-level estimate:
5.1. FINAL ESTIMATE=CES STATE EMP×((final weight JOLTS rate×CMW)+(synthetic rate×CMW))
6. To stabilize the estimate, the sum of state Composite Synthetic model estimates within each region is then benchmarked to the published JOLTS regional estimates.
State-level JOLTS estimates for hires and total separations come directly from the model outlined above. Synthetic job openings ![]() are a function of the ratio of industry-regional job openings and hires
are a function of the ratio of industry-regional job openings and hires ![]() . This ratio of published job openings to hires is applied to model hires estimates
. This ratio of published job openings to hires is applied to model hires estimates ![]() to derive model job opening estimates. Ratio-adjusting the JOLTS model hires and separations to the regional published JOLTS hires and separations estimates ensures that the JOLTS published churn rate is fully accounted for.
to derive model job opening estimates. Ratio-adjusting the JOLTS model hires and separations to the regional published JOLTS hires and separations estimates ensures that the JOLTS published churn rate is fully accounted for.
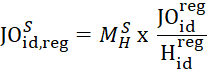
Synthetic quits and layoffs and discharges are a function of the relative percentage of the individual components of total separations at the industry-regional level ![]() . The relative percentages of each component are applied to the model separations estimates
. The relative percentages of each component are applied to the model separations estimates ![]() ) to derive model quits and layoffs and discharges
) to derive model quits and layoffs and discharges ![]() .
.
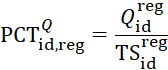
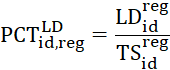
![]()
![]()
This approach is not meant to model individual QCEW-LDB data records. It would not be prudent to use this approach to model small populations (30 or fewer establishments). The model works best at the state-level, and while it is possible to model smaller populations, there potentially is a reduction in the strength of the model proportionate to the reduction in the size of the population being modeled.
The model does generate state-level job openings and separations breakouts. However, these estimates are based upon ratios that are common across the region to which a state belongs. If there are significant differences in the ratio of job openings to hires or separations breakouts for any particular state (or set of states) within a region, the model cannot detect that and estimates will not reflect those differences.
Since the model is based on QCEW-LDB data, the model cannot produce current state-level estimate since QCEW-LDB data lags current JOLTS estimation production by 6–9 months. These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which will be updated annually in June.
The Extended Composite Synthetic model is designed to project the Composite Synthetic forward until QCEW-LDB data are available to produce Composite Synthetic estimates. The Composite Synthetic estimates are extended using the ratio of the current Composite Regional state industry estimate to the Composite Regional state industry estimate from 1 year ago. This approach ensures that the Extended Composite Synthetic state estimates reflect current JOLTS regional and industry-level economic conditions. The Extended Composite Synthetic estimates reflects current JOLTS state economic conditions to the extent that sufficient JOLTS microdata are available.
Extended Composite Synthetic model inputs
The following are inputs into the Extended Composite Synthetic model:
The Composite Synthetic model estimates are produced at a lag since QCEW-LDB data are only available at a 6- to 9-month lag relative to JOLTS data. The Composite Regional model estimates, in contrast, are not produced at a lag and are available concurrent with JOLTS data. Therefore, Composite Synthetic estimates can be extended by ratio-adjusting the Composite Synthetic estimates by the ratio of current Composite Regional estimates to the Composite Regional estimates from the previous year at the state-industry-level as follows:
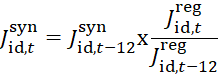
where,
![]() is the extended composite synthetic state industry estimate for month t
is the extended composite synthetic state industry estimate for month t
![]() is the composite synthetic state industry estimate for month t−12 (previous year)
is the composite synthetic state industry estimate for month t−12 (previous year)
![]() is the Composite Regional state industry estimate for month t
is the Composite Regional state industry estimate for month t
![]() is the Composite Regional state industry estimate for month t−12 (previous year).
is the Composite Regional state industry estimate for month t−12 (previous year).
State-level estimates are produced by summing the extended composite synthetic estimates over industry.
This model will produce state-level estimates of job openings, hires, quits, layoffs and discharges, and total separations. These estimates are produced without lag. The methodology allows the Extended Composite Synthetic data to reflect current economic trends at the CES Industry–JOLTS Region level. The projection reflects current state economic trends where sufficient JOLTS microdata are available.
These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which are updated annually in June.
Winsorization is a process used to safeguard against extreme values or outliers that potentially could unduly impact a forecasted estimate. The technique for JOLTS state estimates involves identifying monthly outliers by state and data element and replacing them with winsorized values. Although unusually high values are rare, having safeguards against extreme values will lessen the impact of these anomalies and reduce the volatility in JOLTS state estimates.
The state estimates are based on a composite model of QCEW data and JOLTS reported data. However, while current JOLTS reported data are available at the time of production, current QCEW data are not. Consequently, JOLTS state estimates are forecasted using the previous year’s QCEW estimate and JOLTS regional rates. By definition, the year-ago QCEW estimate is multiplied by the ratio of the current regional estimate to the year-ago regional estimate at the Current Employment Statistics-State and Area (CES-SA) ID level.
The ratio of the current regional estimate to the year-ago regional estimate at the CES-SA ID level ratio of the current regional estimate to the year-ago regional estimate at the CES-SA ID level is winsorized. The winsorization cutoffs are the historical 99th percentile of regional ratios for each variable (job openings, hires, quits, layoffs and discharges, and other separations). Even though other separations are not published for state estimates it is still identified in the winsorization process as it is one of the components to total separations.
Unit and item response rates are tracked monthly to measure data quality and usability. Refusal rates, initiation rates, and collection rates are also calculated and monitored.
JOLTS estimates are subject to two types of error: sampling error and nonsampling error.
Sampling error can result when a sample, rather than an entire population, is surveyed. There is a chance that the sample estimates may differ from the true population values they represent. The exact difference, or sampling error, varies with the sample selected, and this variability is measured by the standard error of the estimate. BLS analysis is generally conducted at the 90-percent level of confidence. This means that there is a 90-percent chance that the true population mean will fall into the interval created by the sample mean plus or minus 1.65 standard errors. Estimates of the median standard errors are released monthly as part of the significant change tables on the JOLTS webpage and are available upon request. Standard errors are updated annually with the most recent 5 years of data.
The JOLTS estimates are also affected by nonsampling error. Nonsampling error can occur for many reasons including the failure to include a segment of the population, the inability to obtain data from all units in the sample, the inability or unwillingness of respondents to provide data on a timely basis, mistakes made by respondents, errors made in the collection or processing of the data, and errors from the employment benchmark data used in estimation.
The JOLTS program uses quality control procedures to reduce nonsampling error in the survey’s design. See the Data Sources section.