Handbook of Methods > Occupational Employment and Wage Statistics > Archives > August 31, 2020

Handbook of Methods Occupational Employment and Wage Statistics Calculation

Occupational Employment and Wage Statistics: Calculation

Each semiannual sample represents roughly one-sixth of the establishments for the full 6-panel sample plan. Each sample is used in conjunction with the previous five semiannual samples in order to create a combined sample of approximately 1.1 million establishments. This includes only the most recent data for federal and state government. In this cycle, data collected in May 2019 are combined with data collected in November 2018, May 2018, November 2017, May 2017, and November 2016.

Of the approximately 1.1 million establishments in the 50 states and the District of Columbia in the combined initial sample, approximately 1,067,000 were viable establishments (that is, establishments that are not outside the scope or out of business). Of the viable establishments, approximately 756,000 responded and 311,000 did not—a 70.9-percent response rate. The response rate in terms of weighted sample employment is 67.7 percent.

Preparing data for estimation

Sample data must be correctly prepared prior to computation of occupational employment and wage estimates and estimates of their variance. Data for sampled nonrespondents are imputed and benchmarking factors are computed before estimation. This is necessary for sampled data from the current panel to be reweighted to correctly reflect industrial employment levels recorded in the U.S. Bureau of Labor Statistics Quarterly Census of Employment and Wages (QCEW).

Nonresponse

Nonresponse is a chronic problem in virtually all large-scale surveys because it may introduce a bias in estimates if the nonrespondents tend to differ from respondents in terms of the characteristic being measured. To partially compensate for nonresponse, the missing data for each nonrespondent are imputed using plausible data from responding units with similar characteristics.

Preparing data for estimation

Data for sampled nonrespondents are imputed and benchmarking factors are computed before estimation. This is necessary for sampled data from the current panel to be reweighted to correctly reflect industrial employment levels recorded in the U.S. Bureau of Labor Statistics Quarterly Census of Employment and Wages (QCEW).

Establishments that do not report occupational employment data are called “unit” nonrespondents. Establishments that report employment data but fail to report some or all of the corresponding wages are called “partial” nonrespondents. Missing data for unit nonrespondents are imputed through a two-step imputation process. Missing data for partial nonrespondents are imputed through the second step of the process only.

Step 1, Impute an occupational employment staffing pattern

For each unit nonrespondent, a staffing pattern is imputed using a nearest-neighbor “hot deck” imputation method. The procedure links a responding donor establishment to each nonrespondent. The nearest-neighbor hot deck procedure searches within defined cells for a donor that most closely resembles the nonrespondent by geographic area, industry, and employment size. Ownership is also used in the hospital, education, gambling, and casino hotel industries. The procedure initially searches for a donor whose reported employment is approximately the same as the nonrespondent’s frame employment within the same 5- or 6-digit NAICS (North American Industry Classification System) or NAICS aggregation, state, and ownership. If more than one otherwise equally qualified donor is found, a donor from a more recent panel will be selected over a donor from an older panel. If the search is unsuccessful, the pool of donors is enlarged in incremental steps by expanding geographic area and industry until a suitable donor is found. Limits are placed on the number of times a donor can be used.

After a donor has been found, its occupational staffing pattern is used to prorate the nonrespondent’s frame employment by occupation. The prorated employment is the nonrespondent’s imputed occupational employment.

Step 2, Impute an employment distribution across wage intervals

For each “unit” nonrespondent in step 1 or for each “partial” nonrespondent, impute an employment distribution across wage intervals for occupations without complete wage data. This distribution, called the wage employment distribution, is imputed as follows:

· Identify the imputation cell for each of the nonrespondent’s occupations. Imputation cells are initially defined by MSA (Metroplitan Statistical Area) / BOS (Balance of State), NAICS 5/6 or NAICS aggregation, and size class from the most recent panel only. For schools, hospitals, gambling establishments, and casino hotels, cells are further divided by ownership.

· Determine if the imputation cell has enough respondents to compute wage employment distributions. If not, incrementally enlarge the cell until there are enough respondents.

· Use the distributions above to prorate the nonrespondent’s imputed occupational employment across wage intervals. (Or, for partial respondents, use the distributions above to prorate the reported occupational employment across wage intervals.)

Special procedures

Within the past 3-year cycle, the OES had critical nonrespondents that could not be imputed using current OES methods. The OES employed special imputation procedures that used nonrespondents’ prior staffing patterns. The occupational employment was benchmarked to the current year and the wage distribution was imputed using procedures very similar to the current partial imputation method.

Reweighting for the combined sample

Employment and wage rate estimates are computed using a rolling 6-panel (3-year) sample. Establishments from each panel’s sample are initially assigned weights as if one panel were being used to represent the entire population. When the samples are combined, each sampled establishment must be reweighted so that the aggregated sample across 6 panels represents the entire population. Establishments selected with certainty in the 6-panel cycle are given a weight equal to 1. Noncertainty units are reweighted stratum by stratum. This revised weight is called the 6-panel combined sample weight. The original single-panel sampling weights are computed so that responses in a stratum could be weighted to represent the entire stratum population. In one common scenario, 6-panel samples are combined, and all 6 panels have sample units for a particular stratum. A summation of the single-panel weights would over-represent the population by a factor of six. Because we do not want to over-represent the stratum population, the 6-panel combined sample weight of each establishment is set equal to 1/K times its single-panel sampling weight. In general, when 6-panel samples are combined, a count of the number of panels with at least one unit selected for a given stratum is assigned to K.

Benchmarking to QCEW employment

A sum of ratio-adjusted weighted reported occupational employment is used to calculate estimates of occupational employment. The auxiliary variable for the estimator is the average of the latest May and November employment totals from the BLS Quarterly Census of Employment and Wages (QCEW). For the May 2019 estimates, the auxiliary variable is the average of May 2019 and November 2018 employment. To balance the states’ need for estimates at differing levels of geography and industry, the ratio estimation process is carried out through a series of four hierarchical employment ratio adjustments. The ratio adjustments are also known as benchmark factors (BMFs).

The first of the hierarchical benchmark factors is calculated for cells defined by state, MSA/BOS, NAICS 3/4/5/6, and employment size class (4 size classes: 1-19, 20-49, 50-249, 250+). For establishments in the hospital and education industries (NAICS 622 and 611), the first hierarchical factor is calculated for cells defined by state, MSA/BOS, NAICS 3/4/5/6, employment size class (4 size classes: 1-19, 20-49, 50-249, 250+), and ownership (state government, local government, or privately owned). If a first-level BMF is out of range, it is reset to a maximum (ceiling) or minimum (floor) value. First-level BMFs are calculated as follows:

h = MSA/BOS by NAICS 3/4/5/6

H = state by NAICS 3/4/5/6

s = employment size classes (1-19, 20-49, 50-249, 250+)

S = aggregated employment size classes (1-49, 50+)

o = ownership (state government, local government, or privately owned)

M = average of May and November QCEW employment

w_i = six-panel combined sample weight for establishment i

x_i= total establishment employment

BMF_min = a parameter, the lowest value allowed for BMF

BMF_max = a parameter, the highest value allowed for BMF

$β_{hs} = (\frac{M_{hs}}{\sum i \in hs w_{i} x_{i}})$ , $β_{hS} = (\frac{M_{h}}{\sum i \in hS w_{i} x_{i}})$ , $β_{h} = (\frac{M_{h}}{\sum i \in h w_{i} x_{i}})$

$β_{hso} = (\frac{M_{hso}}{\sum i \in hso w_{i} x_{i}})$ , $β_{hSo} = (\frac{M_{hSo}}{\sum i \in hSo w_{i} x_{i}})$ , $β_{ho} = (\frac{M_{h}}{\sum i \in ho w_{i} x_{i}})$ , then

$BM F_{1, hs} = \{\begin{matrix} β_{hso}, if all β_{hso} within h are bounded by (BM F_{min}, BM F_{max}), \\ β_{hs}, if all β_{hs} within h are bounded by (BM F_{min}, BM F_{max}), \\ β_{hSo}, if all β_{hSo} within h are bounded by (BM F_{min}, BM F_{max}), \\ β_{hS}, if all β_{hS} within h are bounded by (BM F_{min}, BM F_{max}), \\ β_{ho}, if all β_{ho} within h are bounded by (BM F_{min}, BM F_{max}), \\ β_{h}, if all β_{h} within h are bounded by (BM F_{min}, BM F_{max}), \\ BM F_{min}, if β_{h} <BM F_{min}, \\ BM F_{max}, if β_{h} >BM F_{max} \end{matrix}$

Second-level BMFs are calculated for cells defined at the state, NAICS 3/4/5/6 level by summing the product of combined 6-panel weight and first-level BMF for each establishment in the cell. For establishments in the hospital, education, gambling, and casino hotel industries (NAICS 622, 611, 7132 and 72112), the first hierarchical of the second-level BMK factor is calculated at the state, NAICS 3/4/5/6, and ownership level. Second-level BMFs account for the portion of universe employment that is not adequately covered by weighted employment in first-level benchmarking. Inadequate coverage occurs when “MSA/BOS | NAICS 3/4/5/6 | size class” cells have no sample data or when a floor or ceiling is imposed on first-level BMFs. Second-level benchmarks are calculated as follows:

$β_{Ho} = (\frac{M_{Ho}}{\sum hs \in H \sum_{i \in hs} w_{i} x_{i} BM F_{1, hs}})$

$β_{H} = (\frac{M_{H}}{\sum hs \in H \sum_{i \in hs} w_{i} x_{i} BM F_{1, hs}})$ , then

$BM F_{2,H} = \{\begin{matrix} β_{Ho}, if all β_{Ho} within H are bounded by (BM F_{min}, BM F_{max}), \\ β_{H}, if all β_{H} within H are bounded by (BM F_{min}, BM F_{max}), \\ BM F_{min}, if β_{H} <BM F_{min}, \\ BM F_{max}, if β_{H} >BM F_{max} \end{matrix}$

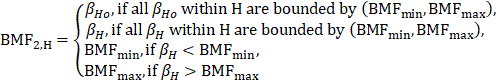
Third-level BMFs (BMF_3,H) are calculated at the “State | 3-digit NAICS” cell level by summing the product of combined 6-panel weight, first-level BMF, and second-level BMF for each establishment in the cell. The third-level BMF also benchmarks by ownership for the hospital, education, gambling, and casino hotel industries. Fourth-level BMFs (BMF_4,H) are calculated at the “State | 2-digit NAICS” cell level by summing the product of final weight, first-level BMF, second-level BMF, and third-level BMF for each establishment in the cell. The fourth-level BMK factor does not benchmark by ownership. As with second-level BMFs, third- and fourth-level BMFs are computed to account for inadequate coverage of the universe employment.

A final benchmark factor, BMFi, is calculated for each establishment as the product of its four hierarchical benchmark factors (BMF_i = BMF₁ * BMF₂ * BMF₃ * BMF₄). A benchmark weight value is then calculated as the product of the establishment’s six-panel combined sample weight and final benchmark factor.

Estimation methodology

OES produces estimates of occupational employment totals, mean wage rates, and wage rate percentiles. Variance estimates are produced via jackknife random group and Taylor series linearization methods.

Occupational employment estimates

Benchmark factors and the combined 6-panel weights are used to compute estimates of occupational employment. Estimates are produced for cells defined by geographic area and industry group. The total employment for an occupation in a cell is estimated by taking the product of the reported occupational employment, the 6-panel combined sample weight, and the final benchmark factor for each establishment in the cell, and summing the product across all establishments in the cell. This sum is the estimate of total occupational employment in the cell.

The equation below is used to calculate occupational employment estimates for an estimation cell defined by geographic area, industry group, and size class.

${\hat{X}}_{ho} = \sum i \in h (w_{i} BM F_{i} x_{io})$

where

o = occupation

h = estimation cell

w_i = six-panel combined sample weight for establishment i

BMF_i = final benchmark factor for establishment i

x_io = employment for occupation o in establishment i

${\hat{X}}_{ho}$ = estimated employment for occupation o in cell h

Wage rate estimation

Two externally derived parameters are used to calculate wage rate estimates. They are:

· the mean wage rates for each of the 12 wage intervals and

· wage updating factors (also known as aging factors)

Wage rates of workers are converted to 1 of 12 consecutive, nonoverlapping wage bands. Individual wage rates are used for federal government and U.S. Postal Service workers. State governments may report their data as either individual wage rates or interval wage rates.

An illustration

An establishment employs 10 secretaries at the following wage rates:

$9/hour 1 secretary

$10/hour 1 secretary

$12/hour 2 secretaries

$13/hour 2 secretaries

$14/hour 2 secretaries

$16/hour 1 secretary

$17/hour 1 secretary

Wage rates for secretaries, however, are used in the OES survey as follows:

Wage interval A (under $9.25/hour) 1 secretary

Wage interval B ($9.25-$11.74/hour) 1 secretary

Wage interval C ($11.75-$14.74/hour) 6 secretaries

Wage interval D ($14.75-$18.74/hour) 2 secretaries

The remaining wage intervals have 0 secretaries.

Because wage rates are grouped into intervals, we must use grouped data formulas to calculate estimates of mean and percentile wage rates. Assumptions are made when using grouped data formulas. For the mean wage rate formula, we assume that we can calculate the average wage rate for workers in each interval. For the percentile wage rate formula, we assume that workers are evenly distributed in each interval.

Wage data from the May 2019, November 2018, May 2018, November 2017, May 2017, and November 2016 panels were used to calculate May 2019 wage rate estimates. Wage data from different panels, however, are not equivalent in real-dollar terms due to inflation and changing compensation costs. Consequently, wage data collected prior to the current survey reference period have to be updated or aged to approximate that period.

Determining a mean wage rate for each interval

The mean hourly wage rate for all workers in any given wage interval cannot be computed using grouped data collected by the OES survey. This value is calculated externally using data from the BLS National Compensation Survey (NCS). With the exception of the highest wage interval, mean wage rates for each panel are calculated using the most recent NCS data available. The hourly mean wage rate of the highest wage interval is calculated differently from the others. A weighted average of the previous 3 years’ means is used, instead of just the current year’s mean. Note that the mean hourly wage rate for interval L (the upper, open-ended wage interval) is calculated without wage data for pilots. This occupation is excluded because pilots work fewer hours than workers in other occupations.

Wage aging process

Aging factors are developed from the Bureau’s Employment Cost Index (ECI) survey. The ECI survey measures the rate of change in wages and salaries for ten major occupational groups on a quarterly basis. Aging factors are used to adjust OES wage data from past survey reference periods to the current survey reference period. The procedure assumes that there are no major differences by geography, industry, or detailed occupation within the occupational division. The twelfth, open-ended, interval is not aged.

Mean hourly wage rate estimates

For data from private sector, local government, and certain state government establishments, the mean hourly wage is calculated as the total weighted hourly wages for an occupation divided by its weighted survey employment. Estimates of mean hourly wages are calculated using a standard grouped data formula that was modified to use ECI aging factors as:

${\hat{R}}_{o} = \frac{\sum_{z = t - 5}^{t} (\sum i \in z w_{i} BM F_{i} {\hat{y}}_{io})}{{\hat{X}}_{o}}$

where

${\hat{y}}_{io}$ ${\hat{y}}_{io}$ ${\hat{y}}_{io}$ $= u_{zo} \sum r c_{zr}$ , $(i \in z)$

o = occupation

${\hat{R}}_{ο}$ ${\hat{R}}_{o}$ = mean hourly wage rate for occupation o

z = panel (or year)

t = current panel

w_i = six-panel combined sample weight for establishment i

BMF_i = final benchmark factor applied to establishment i

= unweighted total hourly wage estimate for occupation o in establishment i

r = wage interval

${\hat{X}}_{o}$ ${\hat{X}}_{o}$ = estimated employment for occupation o

x_{i o r} = reported employment for occupation o in establishment i in wage interval r (note that establishment i reports data

for only one panel z or one year z)

u_{z o} = ECI aging factor for panel (or year) z and occupation o

c_{z r} = mean hourly wage for interval r in panel (or year) z

In this formula, c_{z r} represents the mean hourly wage of interval r in panel (or year) z. The mean is computed externally using data from the Bureau’s NCS survey.

For wage rate data from federal and certain state government establishments, the hourly wages for an occupation within an establishment are summed to get total wages. Employment for that occupation within that establishment is also summed to get total employment. The total wages and total employment across all establishments in the occupation for the estimation level of interest are summed.

$Mean Wage = \frac{Total Interval Wages + Total Individual Wages}{Total Interval Employment + Total Individual Employment}$

Percentile hourly wage rate estimates

The p-th percentile hourly wage rate for an occupation is the wage where p percent of all workers earn that amount or less and where (100-p) percent of all workers earn that amount or more. The wage interval containing the p-th percentile hourly wage rate is located using a cumulative frequency count of estimated employment across all wage intervals. After the targeted wage interval is identified, the p-th percentile wage rate is then estimated using a linear interpolation procedure. This statistic is calculated by first distributing federal, state, local government, and private sector workers inside each wage interval. Federal and certain state government workers are distributed throughout the wage intervals according to their wage rates, while certain state government, local government, and private sector workers are distributed uniformly within each wage interval. Next, workers are ranked from lowest paid to highest paid. Finally, the product of the total employment for the occupation and the desired percentile is calculated to determine the worker that earns the p-th percentile wage rate.

$p R_{o} = L_{r} + \frac{j}{f_{r}} (U_{r} - L_{r})$

where

${pR}_{o}$ ${pR}_{o}$ = p-th percentile hourly wage rate for occupation o

r = wage interval that encompasses

$L_{r}$ = lower bound of wage interval r

$U$ , = upper bound of wage interval r

$f_{r}$ = number of workers in interval r

j = difference between the number of workers needed to reach the p-th percentile wage rate and

the number of workers needed to reach the L_r wage rate

Annual wage rate estimates

These estimates are calculated by multiplying mean or percentile hourly wage rate estimates by a “year-round, full time” figure of 2,080 hours (52 weeks x 40 hours) per year. These estimates, however, may not represent mean annual pay should the workers work more or less than 2,080 hours per year.

Alternatively, some workers are paid on an annual basis but do not work the usual 2,080 hours per year. For these workers, survey respondents report annual wages. Hourly wage rates cannot be derived from annual wage rates with any reasonable degree of confidence because the OES survey does not collect the actual number of hours worked. Only annual wages are reported for some occupations.

Occupational employment variance estimation

A subsample replication technique called the “jackknife random group” is used to estimate variances of occupational employment. In this technique, each sampled establishment is assigned to one of G random groups. G subsamples are created from the G random groups. Each subsample is reweighted to represent the universe.

G estimates of total occupational employment ( ${\hat{X}}_{hjog}$ (one estimate per subsample) are calculated. The variability among the G employment estimates is a good variance estimate for occupational employment. The two formulas below are used to estimate the variance of occupational employment for an estimation cell defined by geographic area and industry group.

$v ({\hat{X}}_{hjo}) = \frac{\sum_{g = 1}^{G} {({\hat{X}}_{h} - {\hat{\overset{̅}{X}}}_{h})}^{2}}{G(G - 1)}$

where

h = estimation cell defined by geographic area and industry group

j = employment size class (1-19, 20-49, 50-249, 250+)

o = occupation

$v({\hat{X}}_{hjo})$ = estimated variance of ${\hat{X}}_{hjo}$

G = number of random groups

${\hat{X}}_{hjo}$ ${\hat{X}}_{hjo}$ = estimated employment of occupation o in cell h and size class j

${\hat{X}}_{hjog}$ = estimated employment of occupation o in cell h, size class j, and subsample g

${\hat{\overset{̅}{X}}}_{hjo}$ ${\hat{\overset{̅}{X}}}_{hjo}$ = estimated mean employment for occupation o in cell h and size class j based on the

G subsamples (Note: a finite population correction factor is applied to the terms and )

The variance for an occupational employment estimate in cell h is obtained by the equation:

$v ({\hat{X}}_{ho}) = \sum j \in h v ({\hat{X}}_{hjo})$

This sums the variances $v({\hat{X}}_{hjo}^{})$ across all size classes j in the cell.

Occupational mean wage variance estimates

Because the OES wage data are placed into intervals (grouped), the exact wage of each worker is not used. Therefore, some components of the wage variance are approximated using factors developed from NCS data. A Taylor Series Linearization technique is used to develop a variance estimator appropriate for OES mean wage estimates. The primary component of the mean wage variance, which accounts for the variability of the observed sample data, is estimated using the standard estimator of variance for a ratio estimate. This component is the first term in the formula given below:

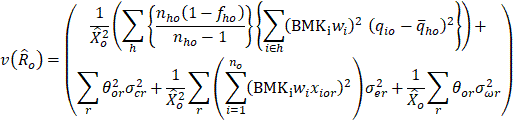
$v ({\hat{R}}_{o}) = (\begin{matrix} \frac{1}{{\hat{X}}_{o}^{2}} (\sum h \{\frac{n_{ho} (1 - f_{ho})}{n_{ho} - 1}\} \{\sum i \in h {(BM K_{i} w_{i})}^{2} {(q_{io} - {\overset{̅}{q}}_{ho})}^{2}\}) + \\ \sum r θ_{or}^{2} σ_{cr}^{2} + \frac{1}{{\hat{X}}_{o}^{2}} \sum r (\sum_{i = 1}^{n_{o}} {(BM K_{i} w_{i} x_{ior})}^{2}) σ_{er}^{2} + \frac{1}{{\hat{X}}_{o}} \sum r θ_{or} σ_{ωr}^{2} \end{matrix})$

where

$|{\hat{R}}_{o}|$ = estimated mean wage for occupation o

$v ({\hat{R}}_{o})$ = estimated variance of

= estimated occupational employment for occupation o

h = stratum (area/industry/size class)

$f_{ho}$ = sampling fraction for occupation o in stratum h

$n_{ho}$ = number of sampled establishments that reported occupation o in stratum h

$w_{i}$ = six-panel combined sample weight for establishment i

BMF_i = final benchmark factor applied to establishment i

$q_{io}$ = $({\hat{y}}_{io} - {\hat{R}}_{o} x_{io})$ for occupation o in establishment i

= estimated total occupational wage in establishment i for occupation o

$x_{ior}$ $x_{ior}$ $x_{ior}$ = reported employment in establishment i for occupation o

= mean of the q_io quantities for occupation o in stratum h

$θ_{or}$ = proportion of employment within interval r for occupation o

= reported employment in establishment i within wage interval r for occupation o

$(σ_{cr}^{2}, σ_{er}^{2}, and σ_{ωr}^{2})$ = Within wage interval r, these are estimated using the NCS and, respectively, represent the variability of

the wage value imputed to each worker, the variability of wages across establishments, and the variability

of wages within establishments.

Reliability of the estimates

Estimates developed from a sample will differ from the results of a census. An estimate based on a sample survey is subject to two types of error: sampling and nonsampling error. An estimate based on a census is subject only to nonsampling error.

Nonsampling error

This type of error is attributable to several causes, such as errors in the sampling frame; an inability to obtain information for all establishments in the sample; differences in respondents' interpretation of a survey question; an inability or unwillingness of the respondents to provide correct information; errors made in recording, coding, or processing the data; and errors made in imputing values for missing data. Explicit measures of the effects of nonsampling error are not available.

Sampling error

When a sample, rather than an entire population, is surveyed, estimates differ from the true population values that they represent. This difference, the sampling error, occurs by chance and its variability is measured by the variance of the estimate or the standard error of the estimate (square root of the variance). The relative standard error is the ratio of the standard error to the estimate itself.

Estimates of the sampling error for occupational employment and mean wage rates are provided for all employment and mean wage estimates to allow data users to determine if those statistics are reliable enough for their needs. Only a probability-based sample can be used to calculate estimates of sampling error. The formulas used to estimate OES variances are adaptations of formulas appropriate for the survey design used.

The particular sample used in the OES survey is one of a large number of many possible samples of the same size that could have been selected using the same sample design. Sample estimates from a given design are said to be unbiased when an average of the estimates from all possible samples yields the true population value. In this case, the sample estimate and its standard error can be used to construct confidence intervals, or ranges of values that include the true population value with known probabilities. To illustrate, if the process of selecting a sample from the population were repeated many times, if each sample were surveyed under essentially the same unbiased conditions, and if an estimate and a suitable estimate of its standard error were made from each sample, then:

1. Approximately 68 percent of the intervals from one standard error below to one standard error above the estimate would include the true population value. This interval is called a 68-percent confidence interval

2. Approximately 90 percent of the intervals from 1.6 standard errors below to 1.6 standard errors above the estimate would include the true population value. This interval is called a 90-percent confidence interval.

3. Approximately 95 percent of the intervals from 2 standard errors below to 2 standard errors above the estimate would include the true population value. This interval is called the 95-percent confidence interval.

4. Almost all (99.7 percent) of the intervals from 3 standard errors below to 3 standard errors above the estimate would include the true population value.

For example, suppose that an estimated occupational employment total is 5,000, with an associated estimate of relative standard error of 2.0 percent. Based on these data, the standard error of the estimate is 100 (2 percent of 5,000). To construct a 90-percent confidence interval, add and subtract 160 (1.6 times the standard error) from the estimate: (4,840; 5,160). Approximately 90 percent of the intervals constructed in this manner will include the true occupational employment if survey methods are nearly unbiased.

Estimated standard errors should be taken to indicate the magnitude of sampling error only. They are not intended to measure nonsampling error, including any biases in the data. Particular care should be exercised in the interpretation of small estimates or of small differences between estimates when the sampling error is relatively large or the magnitude of the bias is unknown.

Last Modified Date: August 31, 2020