An official website of the United States government
 United States Department of Labor
United States Department of Labor
The Occupational Employment and Wage Statistics (OEWS) program uses a model-based estimation method called MB3 to produce occupational employment and wage estimates from the collected OEWS survey data. Each set of estimates is produced by combining data from 6 semiannual survey panels that are collected over a 3-year period for a total sample of approximately 1.1 million establishments. To produce the May 2024 estimates, data collected for the May 2024 survey panel were combined with data collected in survey panels for November 2023, May 2023, November 2022, May 2022, and November 2021. Federal and state government data are collected by annual census, with only the most recent year of data used in the estimates.
All establishments in the population covered by the OEWS survey are represented in the estimates, either by their reported survey data or by data modeled from similar responding establishments. Establishments that responded to the survey and met certain stability criteria are represented in the estimates by their reported survey data, while all other in-scope establishments in the population receive modeled data. These establishments may be sampled units that responded but did not meet stability criteria, sampled units that did not respond, or in-scope establishments that were not sampled to participate in the OEWS survey. For the occupational employment estimates to sum to total population employment, each in-scope establishment's employment is set to the average of its May and November Quarterly Census of Employment and Wages (QCEW) employment for the two most recent survey panels used in the estimates.
Under MB3, occupational employment and wage estimates are calculated directly from a population containing both establishments with response data and establishments with modeled data. For most industries, the OEWS population consists of in-scope establishments present in QCEW as of the OEWS survey reference period. Each establishment in the population is defined by characteristics including industry, size, ownership, and location, which are known to be strong predictors of occupational employment and wages. OEWS survey response data provide occupational employment distributions, known as staffing patterns, and wage information for a portion of the population. For the remaining establishments in the population, OEWS response data from the current panel and five previous panels are used to predict staffing patterns and wages.
The prediction framework splits establishments in the population into two categories: observed units and unobserved units. Observed units are stable establishments with response data from the previous 3 years. Stability is determined by comparing the values of several variables reported to the OEWS survey with recent QCEW values for the same establishment, as described in the direct matching section. Observed units are represented in the estimates by their reported survey data.
Unobserved units may be nonsampled units, nonresponding units, or responding units that do not meet stability criteria. For any given unobserved unit, occupational employment and wages are predicted using modeled data from similar responding establishments. Responding units that do not satisfy stability criteria can still be used as donors for unobserved units.
The stability criteria for observed units require that the 6-digit North American Industry Classification System (NAICS) industry, ownership, and metropolitan or nonmetropolitan area reported to the OEWS survey exactly match the establishment's QCEW values for the May reference panel. In addition, the establishment's reported employment must be similar to its population employment, defined as the average of the establishment's most recent May and November QCEW employment for a given survey reference period. An establishment's employment is considered stable if its reported employment is within 50 percent or 5 jobs of its population employment. That is, the establishment fulfills either condition:
![]()
where
![]() = population employment
= population employment
![]() = respondent employment
= respondent employment
During data collection, states can correct the QCEW NAICS, metropolitan and nonmetropolitan area, and previous employment values if they are incorrect. These corrections are applied to the population file prior to the stability calculations so that incorrect population data do not automatically prevent a unit from being classified as stable.
For observed units, the unit's reported staffing pattern is scaled up or down to match the unit's population employment, and wages collected in earlier survey panels are adjusted to reflect wage levels as of the reference date. A small percentage of respondents provide complete staffing patterns, but do not provide complete wage data. For these partial respondents, missing wage data are imputed as described in the imputing nonrespondents for wage modeling section, and the units are then treated as respondents. They will be tested for stability, and if stable, will be used as observed units. They can also be used as donors for unobserved units.
The staffing patterns and wages of unobserved units in the population are predicted using data from nearest neighbor respondents. Responding units that do not pass stability criteria are not representative of the population cell for which they were sampled, but they may be used to predict units in the cell represented by the characteristics they reported to the OEWS survey. A pool of 10 nearest neighbor responding units is typically used to predict each unobserved unit. Unobserved units with identical characteristics are predicted as a group and receive the same donors, so the predicted staffing pattern and wages of any unit of a given size, location, ownership group, and industry will be identical.
Potential donors are assigned a series of five scores that measure the similarity of the donor to the unobserved unit in terms of characteristics like industry and geographic location. Each score can take on values between 0 to 1, with 1 indicating a perfect match between donor and recipient. The five individual scores are then multiplied to produce a single overall score for the potential donor. For a given unobserved unit, a set of (typically) 10 responding units with the highest scores is used for the prediction.1
The scoring function for each predictive factor aims to assign a score value based on the relative importance of that factor. Industry and establishment size as measured by total employment are the strongest predictors of staffing patterns. Therefore, differences in either of these characteristics result in large reductions in match scores. Time and location are also important predictors, but differences in either of these dimensions result in relatively smaller score penalties than are given for industry, size, and ownership differences. The specific score values used in the MB3 system were evaluated using simulation studies. Various proposed scoring functions were tested to generate estimates and the best performing of these were used.
Where establishment a is an unobserved unit and establishment b is a potential donor, each component of the score function accounts for differences between a and b. The overall match score of the potential donor is as follows:
![]()
where
![]()
![]() = score for difference in total employment between a and b
= score for difference in total employment between a and b
![]() = score for difference in time between b and the most recent panel
= score for difference in time between b and the most recent panel
![]() = score for difference in 6-digit NAICS industry between a and b
= score for difference in 6-digit NAICS industry between a and b
![]() = score for difference in ownership between a and b
= score for difference in ownership between a and b
![]() = score for difference in detailed area between a and b.
= score for difference in detailed area between a and b.
The employment component is ![]() , where
, where ![]() and
and ![]() are the employment totals for the respective units. For a potential donor with 20 employees and a unit to be predicted with 15 employees, then this works out to
are the employment totals for the respective units. For a potential donor with 20 employees and a unit to be predicted with 15 employees, then this works out to ![]() .
.
Recently collected data are favored over data collected in previous panels. The time score component that reflects this is ![]() , where
, where ![]() is the number of panels between the collection of data for potential donor b and the reference period. A donor unit observed in the current panel would have
is the number of panels between the collection of data for potential donor b and the reference period. A donor unit observed in the current panel would have ![]() and a donor unit sampled 5 panels previously would have
and a donor unit sampled 5 panels previously would have ![]() .
.
Donors would ideally be in the same industry or ownership group as the unit to be predicted, but they could be in a similar industry or different ownership.
The score component reflecting differences in industry at the detailed, 6-digit NAICS level is calculated as follows:
![]()
Although any difference in industry is given the same penalty, donors are chosen according to a hierarchy and therefore more similar industry matches will be used before more different matches.
The score component reflecting differences in ownership is calculated as follows:
![]()
For example, if an unobserved unit is a private school, a private school donor would have an ownership score of 1, while a public school donor would have an ownership score of 0.5.
Donors in the same geographic area are preferred and are treated at four different matching levels. Units in the same state and metropolitan statistical area (MSA) or nonmetropolitan area have an area match score of 1. Units receive an area match score of 0.75 if they are in two different areas of the same state, but both areas have the same area status—that is, both are MSAs or both are nonmetropolitan areas. Units receive a score of 0.5 if they are in two different areas of the same state, and one area is an MSA and the other is a nonmetropolitan area. Finally, units from different states receive a score of 0.25. The score component reflecting differences in area is calculated as follows:
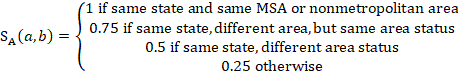
A potential donor from the most recent survey panel and the same MSA or nonmetropolitan area, detailed industry, ownership, and employment level as an unobserved unit will receive a score of 1, the maximum possible score. For a potential donor with 20 employees that would predict a unit of 15 employees ![]() from 2 panels previous to the reference period
from 2 panels previous to the reference period ![]() , with a mismatching industry
, with a mismatching industry ![]() where both are privately owned
where both are privately owned ![]() , and a matching state but differing MSA or nonmetropolitan area, and area status
, and a matching state but differing MSA or nonmetropolitan area, and area status ![]() , the match score is as follows:
, the match score is as follows:
![]()
Depending on the match scores of other potential donors, the unit may or may not be used in prediction.
Potential matches are found by a hierarchical nearest neighbor search detailed in exhibit 1. All establishments with the same employment, NAICS, ownership category, state, and MSA or nonmetropolitan area will be predicted using the same set of donors.
An employment criterion is defined for each level such that the donor's employment must be within a certain percentage of the unobserved unit's employment. For example, in the first hierarchical level, the donor must be in the same state, NAICS, ownership category, and MSA or nonmetropolitan area of the unobserved unit to be predicted while having employment within plus or minus 10 percent of the unobserved unit's employment. Broader industry groups use the most detailed industry level at which OEWS publishes estimates. For most industries, this is the 4-digit NAICS level. For a minority of industries, the published OEWS estimates are defined at the 3-, 5-, or 6-digit NAICS level, or as OEWS-specific combinations of 4-digit industries.
If fewer than 10 potential donors are found at the first level of the hierarchy, the search proceeds through subsequent levels of the hierarchy, stopping when at least 10 suitable donors are found. If fewer than 10 donor units are available at hierarchy level 10, prediction will still proceed if at least 5 donor units are found when the search reaches the highest level. The matches with the highest scores are used for prediction.
|
Exhibit 1. Hierarchical levels of donor matches |
||
|
Hierarchy level |
Characteristics that must match between the prediction cell and responder (donor) |
Employment criterion (in percent) |
|
1 |
State, NAICS, Ownership, MSA or nonmetropolitan area |
10 |
|
2 |
State, NAICS, Ownership, MSA or nonmetropolitan area |
20 |
|
3 |
State, NAICS, Ownership |
10 |
|
4 |
State, NAICS, Ownership |
20 |
|
5 |
State, NAICS group, Ownership |
None |
|
6 |
State, NAICS group |
None |
|
7 |
NAICS, Ownership |
10 |
|
8 |
NAICS, Ownership |
20 |
|
9 |
NAICS |
None |
|
10 |
NAICS group |
None |
|
Note: NAICS is a 6-digit NAICS. NAICS group is the most detailed NAICS level for which OEWS publishes estimates, generally the 4-digit NAICS level. |
||
Staffing pattern and wage data for the 10 closest matches are used to predict the staffing pattern and wages of each unobserved unit. If the closest matches include several donors with the same match score, they will all be used, which may result in more than 10 donors. The total number of jobs predicted for each unobserved unit is represented by the unit's population employment, defined as the average of its May and November QCEW employment for the two most recent survey panels. The unobserved unit's occupational staffing pattern is calculated as a weighted average of the donor staffing patterns.
Within a given set of selected donors, donors that are closer matches contribute more to the prediction than donors that do not match as closely. Each selected donor's contribution to the staffing pattern prediction is proportional to its relative match score, defined as the donor's individual match score divided by the total combined scores of all the selected donors. The relative match score ![]() of any match
of any match ![]() among 10 matches,
among 10 matches, ![]() , is as follows:
, is as follows:
![]()
For a given unobserved unit U and set of matches ![]() , the predicted employment E for occupation O in wage interval M will be
, the predicted employment E for occupation O in wage interval M will be
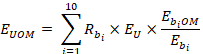
where
![]() is the employment in wage interval M for the occupation O in establishment
is the employment in wage interval M for the occupation O in establishment ![]()
![]() is the employment for establishment
is the employment for establishment ![]()
![]() is the employment of the unit to be predicted
is the employment of the unit to be predicted
![]() is the relative match score of match
is the relative match score of match ![]() .
.
Wages are predicted separately for each occupation in the unobserved unit's staffing pattern based on the subset of staffing pattern donors reporting that specific occupation. The wage for occupation O in interval M for establishment ![]() is represented by
is represented by ![]() . For responding establishments,
. For responding establishments, ![]() is the wage value that will represent them as observed units and as donors to unobserved units that receive modeled data. The establishment's reported wage rates are used as
is the wage value that will represent them as observed units and as donors to unobserved units that receive modeled data. The establishment's reported wage rates are used as ![]() whenever wage rate data are available for all the establishment's employment in the occupation. If any interval wage data are available for a given establishment and occupation, then employees are assigned values of
whenever wage rate data are available for all the establishment's employment in the occupation. If any interval wage data are available for a given establishment and occupation, then employees are assigned values of ![]() sampled from a wage distribution. Donor wage values are scaled using a wage adjustment factor if a match differs from the unobserved unit in industry, ownership, area, employment, or survey panel. Methods for processing interval wage data and modeling wage adjustment factors are discussed in the following sections.
sampled from a wage distribution. Donor wage values are scaled using a wage adjustment factor if a match differs from the unobserved unit in industry, ownership, area, employment, or survey panel. Methods for processing interval wage data and modeling wage adjustment factors are discussed in the following sections.
A random subset of donor wages is used to predict wages for each wage interval within each occupation for unobserved units. If employment is reported for an occupation and wage interval for at least five donors, then it is expected that five donor wages will be used, but at minimum one donor wage will be used. If fewer than five donors are available for an occupation and wage interval, it is likely that all donor wages will be used. For each wage interval, donor wages are sampled using Poisson sampling, with a target of five wages for each wage interval. A systematic sample of a single unit is also taken for use in the case where no wage is sampled using Poisson sampling. The probability of selection for a given donor wage within a given wage interval in the Poisson sample is calculated as follows:
![]()
The probability of selection for systematic sampling is one-fifth of the probability for Poisson sampling.
The occupational wage w predicted for unit U for wage interval M is derived from a weighted composite of the occupational employment of the donor units. Assuming 10 donors, this is given by:
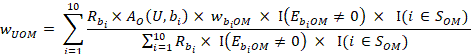
Here, ![]() is the wage adjustment factor discussed under the model-based adjustments section. The function
is the wage adjustment factor discussed under the model-based adjustments section. The function ![]() equals 1 when the establishment's occupational employment is nonzero for a wage interval and equals 0 otherwise. The function
equals 1 when the establishment's occupational employment is nonzero for a wage interval and equals 0 otherwise. The function ![]() equals 1 when the wage of establishment i has been sampled and equals 0 otherwise.
equals 1 when the wage of establishment i has been sampled and equals 0 otherwise.
To illustrate the prediction of an unobserved unit, suppose the unobserved unit U is a jewelry store in a medium-sized MSA. The staffing pattern is predicted for each wage interval of each occupation based on the nearest donors. Detailed below is the prediction for retail salespersons in wage interval C. Suppose that of the 10 nearest respondents available, 8 had employment of retail salespersons in wage interval C. Of those eight, four are other jewelry stores of similar size in the same MSA and most recent survey panel. Three are other jewelry stores in the same MSA with larger differences in size. Of those three, one is from one panel back. The last unit is in the same state and most recent panel, of a similar size, but in a different industry and MSA. To predict the employment and wage for retail salespersons in unobserved unit U, wage interval C, see the example data and calculations in exhibit 2.
|
Exhibit 2. Example data for predicting employment and wages |
||
|
Corresponding value |
Value |
Computed quantity |
|
A |
Unit i relative match score |
|
|
B |
Unit i employment in interval C, occupation O |
|
|
C |
Unit i total employment |
|
|
D |
Unobserved unit total employment |
|
|
E |
Unit i occupational employment ratio in interval C, occupation O |
|
|
F |
Wage adjustment factor |
|
|
G |
Unit i wage in interval C, occupation O |
|
|
H |
Poisson sampling indicator |
|
|
I |
Computed unit i employment share in wage interval C, occupation O |
|
|
J |
Computed unit i wage share in wage interval C, occupation O |
|
|
Note: N.A. indicates data not applicable. |
||
|
Exhibit 2. Example data for predicting employment and wages |
||||||||||
|
Donor pool |
||||||||||
|
Corresponding value |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
0.116 |
0.116 |
0.116 |
0.113 |
0.113 |
0.110 |
0.107 |
0.097 |
0.088 |
0.022 |
|
B |
4.000 |
3.000 |
0.000 |
2.000 |
3.000 |
7.000 |
8.000 |
0.000 |
3.000 |
11.000 |
|
C |
21.000 |
21.000 |
21.000 |
22.000 |
20.000 |
19.000 |
18.000 |
21.000 |
25.000 |
21.000 |
|
D |
21.000 |
21.000 |
21.000 |
21.000 |
21.000 |
21.000 |
21.000 |
21.000 |
21.000 |
21.000 |
|
E |
0.190 |
0.143 |
0.000 |
0.091 |
0.150 |
0.368 |
0.444 |
0.000 |
0.120 |
0.524 |
|
F |
1.000 |
1.000 |
1.000 |
1.000 |
1.000 |
0.900 |
1.000 |
1.030 |
1.030 |
1.100 |
|
G |
13.250 |
13.250 |
N.A |
13.250 |
13.250 |
13.250 |
13.250 |
N.A |
13.050 |
13.250 |
|
H |
0.000 |
1.000 |
0.000 |
0.000 |
1.000 |
0.000 |
1.000 |
0.000 |
1.000 |
0.000 |
|
I |
0.463 |
0.348 |
0.000 |
0.216 |
0.356 |
0.850 |
0.998 |
0.000 |
0.222 |
0.242 |
|
J |
0.000 |
3.625 |
0.000 |
0.000 |
3.531 |
0.000 |
3.344 |
0.000 |
2.790 |
0.000 |
|
Note: N.A. indicates data not applicable. |
||||||||||
Summing the second-to-last line ("computed unit i employment share") of exhibit 2 yields predicted employment of retail salespersons O in wage interval C for establishment U:
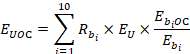
![]()
![]()
Although this does not add up to a whole number, for estimation purposes it is reasonable. Summing the last line of exhibit 2 yields the predicted wage of retail salespersons O in wage interval C for establishment U:
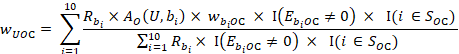
![]()
![]()
When this process is completed for all occupations and wage interval levels observed in the donor units, the predicted wage and employment profile of establishment U can be used for estimation. If the predicted wage is less than the state or federal minimum wage, the predicted wage will be set to the state or federal minimum wage (whichever is higher).
Wage data for three types of units require additional adjustments before being used to calculate wage estimates: units with interval wage data, observed units from earlier survey panels, and unobserved units to be predicted. This wage data processing uses both wage rates and the wage interval groups shown in table 1 in the concepts section.
Using interval data to compute mean wage estimates requires that a wage value be assigned to each employee. MB3 wage estimates use sampled wage rates that are computed using lognormal models fit to each panel of OEWS wage data, aggregated by occupation group and area group.
Predicting unobserved units also requires adjusting wages in the donor units to current local dollars for the unobserved units. For example, suppose an interior design firm (NAICS 541410) in a large metropolitan area and surveyed in a previous survey panel contributes to the wage prediction for an industrial design firm (NAICS 541420) in a small metropolitan area. Occupational wages will differ between these firms due to geography, industry, and time effects. Thus, wages from the first unit must be adjusted with these factors in mind to give a reasonable prediction of the second unit. A fixed effect linear regression model, fit to observed unit data, is the basis for these adjustments. Wages for observed units collected in earlier survey panels are also updated to the reference date using a regression model.
The wage distribution and wage adjustment models are derived from the full OEWS survey sample, which includes both responding and nonresponding establishments. The wage modeling process uses hot deck imputation to impute missing staffing patterns and wages for nonresponding units. For complete nonrespondents that did not provide either staffing patterns or wages, a single nearest neighbor donor is used to impute the entire occupational staffing pattern. This nearest neighbor donor is selected based on industry, state, size class, and, for some industries, ownership.
For each occupation in the imputed staffing pattern, a wage distribution is imputed from a pool of similar respondents reporting that occupation. Partial respondents that reported complete staffing patterns, but did not report complete wage data for some or all of their occupations, also receive imputed wages for any occupations in their staffing patterns that do not have complete wage data. The wage donor search initially looks for donors from the same survey panel, MSA or nonmetropolitan area, 4-digit NAICS, size class, and, for selected industries, same ownership as the recipient. If there are not enough donors to provide wage distributions for the nonrespondents that need them, then the search criteria are loosened and the search repeated. Once a sufficiently large donor pool is found, the donor pool's wage distribution is used to prorate the recipient's reported employment in the occupation across the 12 wage intervals outlined in table 1 in the concepts section.
Once the wage modeling process is complete, the hot deck imputed data for complete nonrespondents are discarded. These units will be treated as unobserved units for estimation and will receive predicted employment and wage data using the MB3 modeling process described earlier. Partial respondents retain their imputed wage distributions (along with their reported staffing patterns) and are treated as respondents thereafter. The interval wage distributions imputed for partial respondents are assigned specific wage values for estimation, as described in the processing interval wage data section.
The wage distribution model and wage adjustment model both use weighted least squares regression to estimate model parameters. Benchmarked sample weights are used in this process, such that weighted employment totals for the current panel will equal QCEW frame values for each industry, state, MSA, and size subgroup.
In MB3, benchmarking factors are used only to adjust data for the purposes of model fitting and are not used directly for estimation. For the May 2024 OEWS estimates, benchmarking uses the average of May 2024 and November 2023 QCEW employment to adjust the weighted reported occupational employment and improve the accuracy of the sampled wage rates and wage adjustment models. The ratio estimation process is carried out through a series of four hierarchical employment ratio adjustments. The ratio adjustments are also known as benchmark factors (BMFs). The BMFs are calculated for the cells defined at each of the following hierarchy levels.
|
Exhibit 3. Hierarchy of benchmark factors |
||||
|
Level |
Area |
Industry |
Size |
Ownership |
|
1 |
MSA/BOS |
NAICS 3/4/5/6 digits |
1-19, 20-49, 50-249, 250+ |
N.A |
|
2 |
State |
NAICS 3/4/5/6 digits |
N.A. |
N.A. |
|
3 |
State |
NAICS 3 digits |
N.A. |
For hospitals, schools, gambling establishments, and casino hotels |
|
4 |
State |
NAICS 2 digits |
N.A. |
N.A. |
|
Note: N.A. denotes not applicable. |
||||
For each establishment, a BMF is generally calculated by finding the ratio of QCEW employment (average of May 2024 and November 2023) to weighted cell OEWS employment for the hierarchy level. There is a universal maximum and minimum BMF value to which the BMF will be set if it is higher than the maximum or lower than the minimum. The second, third, and fourth BMF hierarchy levels are computed to account for inadequate coverage of the universe employment. For example, if an establishment is in a first-level hierarchy cell with no other establishments, other factors will be calculated at the other hierarchy levels to accommodate coverage. The BMFs are dependent upon the establishment's previous hierarchy levels BMFs. A final benchmark factor is calculated for each establishment as the product of its four hierarchical benchmark factors. A benchmark weight value is then calculated as the product of the establishment's six-panel combined sample weight and final benchmark factor.
For respondents with interval wage data, the interval data must be replaced by specific wage rate values for use in estimation and to provide donor wages to the modeling process for unobserved units. Wage rate values assigned to interval data are derived from modeled wage distributions. Wage distributions are modeled for each panel using only weighted data from that panel to represent the population. Occupation and geographic area are the strongest predictors of wages and may cause substantial differences in wage levels between establishments. To provide greater homogeneity within the data, occupations and areas with similar median wages are aggregated into groups.
OEWS assigns occupation group codes to all occupations with median wages in a given wage interval and likewise assigns group codes to all geographic areas with similar median wages. Then, all data with a given ownership status, occupation group, and area group are pooled together for modeling a wage distribution function. The units within an occupation-area-ownership group are not necessarily related in any way other than the wage interval that the median falls into.
Wage distribution modeling incorporates reported wage rate data (specific wages of each employee) from private and local government establishments. The wage distributions for each group are modeled by a lognormal model fit using a log-likelihood expression that incorporates both wage rate and wage interval data.
The assignment of occupation wage groups uses single panel sample weights and reported employment levels within wage intervals to compute the national wage distribution for each detailed occupation and then determine into which interval the median wage for that occupation falls. This determines the wage occupation group for every 6-digit occupation. To be specific, OEWS calculates occupation-specific employment in each of the 12 wage intervals in panel p :
![]()
where
![]() represents the set of panel p OEWS sampled units
represents the set of panel p OEWS sampled units
![]() is the sample weight for establishment e in panel p
is the sample weight for establishment e in panel p
![]() is the reported level of employment in occupation o
is the reported level of employment in occupation o![]() at establishment e in wage interval
at establishment e in wage interval ![]() and panel p.2
and panel p.2
The total occupation-specific employment is then calculated:
![]()
Next, OEWS computes the relative employment shares by wage interval:
![]()
Followed by the computation of cumulative employment shares:
![]()
The detailed occupation o is mapped into the aggregate occupation O in the lowest wage interval that contains at least 50 percent of the detailed occupation's cumulative employment so that each aggregate occupation corresponds to a wage interval:
![]()
Typically, there are either 11 or 12 aggregate occupations corresponding to the various wage intervals.3
For example, if tax preparers, substitute teachers, and fast food cooks all have median wages in interval C, they would be grouped together in occupation group C, and if architectural and civil drafters, actors, and construction and building inspectors all have median wages in interval F, they would be grouped together into occupation group F.
Similarly, OEWS computes the wage distribution for each detailed geographic area (across all occupations) and then determines in which interval the median wage for that area would fall. This determines the aggregate area for every detailed MSA or BOS area. To be specific, OEWS calculates area-specific employment in each of the 12 wage intervals ![]() in the current panel:
in the current panel:
![]()
where
![]() represents the set of panel p OEWS sampled units in area v
represents the set of panel p OEWS sampled units in area v
![]() represents the sampling weight for establishment e in panel p
represents the sampling weight for establishment e in panel p
![]() is the reported level of employment in occupation o
is the reported level of employment in occupation o![]() at establishment e in wage interval
at establishment e in wage interval ![]() and panel p
and panel p
Followed by the calculation of total area-specific employment:
![]()
And the relative employment shares are computed by wage interval:
![]()
OEWS then computes cumulative employment shares:
![]()
The detailed area v is mapped into the aggregate area V into the lowest wage interval that contains at least 50 percent of the detailed area's cumulative employment so that each aggregate area corresponds to a wage interval:
![]()
Typically, there are only three or four aggregate areas, corresponding to interval C, D, E, or F.
For example, if the median wages in San Francisco, CA, and Boston, MA, fall into wage interval F, then these areas will be grouped together in area group F, while if the median wages in Chicago, IL, and Atlanta, GA, fall into wage interval E, these areas will be grouped together in area group E.
Now that OEWS has calculated the separate aggregate occupations and aggregate areas, OEWS combines them to create aggregated area and occupation groups within a wage interval. These aggregate occupation-areas are necessary to correctly adjust the parameters of the lognormal model and subsequently predict local sampled wage rates.
For every possible aggregate occupation-area, denoted as OV, OEWS computes the single panel sample-weighted employment levels for each wage interval:
![]()
where
![]() is the panel p sample in aggregate area V
is the panel p sample in aggregate area V
![]() represents the sampling weight for establishment e in panel p
represents the sampling weight for establishment e in panel p
![]() is the reported level of employment in occupation o
is the reported level of employment in occupation o![]() at establishment e in wage interval
at establishment e in wage interval ![]() and panel p
and panel p
In general, there will be a limited number of aggregate occupation-area groups, typically between 33 and 48.
For example, suppose nurses and paralegals are in occupation group D for a given panel, while doctors and lawyers happen to be in occupation group G. Their employers, a hospital and a law firm, are in different metropolitan areas, but both areas are in area group C. Both employers are also privately owned with ownership code 5. The data for nurses from the hospital and paralegals from the law office are pooled with other data from the same occupation-area-ownership combination to estimate wage group DC5, while the data for doctors in the hospital and lawyers in the law firm are pooled with other data to estimate wage group GC5.
A lognormal model is fit to these aggregated-occupation-by-aggregated-area cells. A maximum likelihood estimator and the sample-weighted employment sums from the current sample are used to estimate the two parameters of the lognormal model for wage w, occupation O, and area V, which falls into a wage interval:
![]()
Local sampled wage rates are predicted using these wage distribution parameter estimates. All data from occupation-area-ownership group OV are used to fit a lognormal model. OEWS then samples a wage for the appropriate wage interval from the wage distribution model. For example, say a paralegal's reported wage falls into wage interval E, while their occupation and geographic location fall into occupation-area-ownership group DC5. This paralegal will be assigned a wage sampled from the lognormal model within the specific occupation-area-ownership aggregate group. Each paralegal in this area reported in interval E will be independently assigned an interval E wage rate that was sampled from the distribution modeled for occupation-area-ownership group DC5.
This process converts all wage interval data to wage rate values. These sampled wage rates, along with usable reported wage rates, directly define wages for all respondents. Respondent wages are adjusted, if needed, to define wages for unobserved units.
Using observed units to predict unobserved units relies on similarity between the units. Wage adjustment is necessary if the unobserved unit differs from donor units in industry, size, location, or time of data collection. Sample response data from the current and previous 2 years are used to fit fixed effect linear regression models for wage adjustments. Coefficients are determined using maximum likelihood estimation over data from the six panels. For a given occupation O, the model is of the form:
![]()
where
![]() = wage
= wage
O = occupation
T = time between the panel of collection and the current panel
![]() = occupation effect across about 850 detailed occupations
= occupation effect across about 850 detailed occupations
![]() = industry-ownership combined effects across about 1,100 detailed NAICS and ownership combinations
= industry-ownership combined effects across about 1,100 detailed NAICS and ownership combinations
![]() = area effect across about 480 detailed areas
= area effect across about 480 detailed areas
![]() = size effect linear coefficient
= size effect linear coefficient
E = total establishment employment
![]() = time effect computed independently for each of 22 major occupational groups
= time effect computed independently for each of 22 major occupational groups
ϵ = error term
Aging factors, which provide adjustments for changes to occupational wages over time, and locality adjustments are both computed directly using wage regression model parameters. All direct match units are separately aged according to a factor based on the combination of year and Standard Occupational Classification (SOC) major group. All donors, including unstable units, are independently adjusted to account for the year and SOC major group combination, detailed occupation, industry, ownership, and size of the unit to be predicted.
Suppose unit b is selected as a donor for unit a. Unit b is one of typically 10 donors for unit a and might come from one or more panels back, in which case unit b's wage data are adjusted to match local current dollars for unit a. The adjusted donor wage for occupation O in unit a based on adjusted unit b data is as follows:
![]()
where
![]()
Occupational employment and wage estimates are computed using observed data and predicted data for the population of about 8.7 million units. After all modeling and wage adjustment is completed, every unit in the population will have either reported or predicted data for occupational employment and wage rates. Employment estimates are computed by summing employment within an estimation cell, while mean wage estimates are computed by dividing summed wages by total employment for an estimation cell. Because all units also are linked to their establishment information, OEWS can also calculate employment, mean wage, and percentile estimates for a mix of industry, ownership, and area levels.
Estimates of occupational employment totals are computed by summing all employment counts of a given occupation over the modeled population data. Estimates are made over area, industry, and ownership. For occupation o, where unit i is any establishment in cell c, the occupational employment estimate is as follows:
![]()
where
xi,o = employment of unit i for occupation o
Mean hourly wages are calculated by summing the hourly wages—reported or predicted—for all employees in the estimation cell and dividing by the total employment in the cell. Employees E in a given occupation and wage interval at a single establishment will all have the same predicted wage w. For establishment i, wage range r, and occupation o in cell c, the computation is as follows:
![]()
where
xiro = employment of unit i for occupation o in wage range r
wiro = wage of unit i for occupation o in wage range r
Percentile wage rate estimates are computed directly from the predicted population using the empirical distribution function with averaging, which is available in many statistical packages.
For most occupations, annual wage estimates are calculated by multiplying mean or percentile hourly wage estimates by a year-round, full-time figure of 2,080 hours (52 weeks × 40 hours) per year. These estimates, however, may not represent annual pay should the workers work more or fewer than 2,080 hours per year.
Although OEWS publishes both annual and hourly wage estimates for most occupations, there are some occupations for which only annual or only hourly wages are published. For example, some workers such as teachers, pilots, and flight attendants are typically paid annual salaries, but work fewer than the usual 2,080 hours per year. Because the survey does not collect the actual number of hours worked, hourly wage rates cannot be derived from annual wage rates with any reasonable degree of confidence. Therefore, only annual wage estimates are published for these occupations. On the other hand, full-time, year-round work may not be typical in some occupations that are usually paid on an hourly basis, such as actors or musicians and singers. For these workers, only hourly wage estimates are published.
Variances for both mean wage estimates and occupational employment estimates are computed using the bootstrap replication technique. Many weights may be associated with a given respondent in MB3 estimates because that respondent may be used to predict multiple unobserved units. This presents problems for many approaches to computing sampling variances. However, bootstrap sample replication is amenable to this design because the full MB3 estimation system may be applied to each replicate sample. Studies that were performed using simulated data informed decisions on the specifics of the bootstrapping approach used here and the number of replicates needed for estimates to converge.
The MB3 variances are computed from 300 bootstrap sample replicates. Each set of replicate estimates is based on a subsample of the full sample and includes model fitting as well as population prediction based on this subsample. The subsample is drawn from the full sample using a stratified simple random sample with replacement design, where the size of the subsample is equal to the size of the full sample. By sampling with replacement, OEWS is up-weighting some sampled units by including them more than once in the subsample and down-weighting others by not including them at all. MB3 selects six independent subsamples, one from each of the six semiannual survey panel samples. The stratification plan is the same used for drawing the full sample—where strata are defined by state, MSAs and nonmetropolitan areas, aggregate NAICS industry, and ownership for schools and hospitals.
Subsampling occurs only for the noncertainty sample units. All certainty units from the full sample are used in every replicate's bootstrap sample. Some strata may only contain a single noncertainty unit, for which a variance cannot be computed. These are referred to as 1-PSU (one primary sampling unit) strata. A collapsing algorithm combines these 1-PSU strata with other like strata to ensure that two or more noncertainty sample units are present in a particular stratum. The collapsing is by the hierarchy detailed in exhibit 4.
|
Exhibit 4. Hierarchical definitions for collapsing 1-PSU (one primary sampling unit) strata |
|
|
Hierarchy level |
Collapse |
|
1 |
Panels*: (0,1), (2,3), and (4,5) |
|
2 |
Panels*: (0,1,2), and (3,4,5) |
|
3 |
Panels*: (0,1,2,3,4,5) |
|
4 |
MSAs |
|
5 |
Allocation NAICS (A_NAICS) |
|
6 |
Nationally |
|
Note: * Panels are labeled 0 to 5, where 0 corresponds to the May 2024 panel. |
|
Sampling variance estimates obtained through these methods do not use the same probabilities used in selection of the full sample, which presents a possible source of error. Analysis indicates that these estimates perform well in estimating sampling variance despite this potential for error.
The six replicate subsamples are combined for calculating MB3 replicate estimates. Single-panel sample weights for the most recent panel are retained for computation of wage distribution model parameters and the wage adjustment factors in each replicate. All matching, wage parameter, and estimation methods described previously are used with each six-panel bootstrap subsample to create occupational employment and wage replicate estimates for every estimation cell. This process is repeated to create 300 sets of replicate estimates. For every estimation cell in which OEWS calculates an estimate, there are occupational employment and mean wage estimates based on the full OEWS sample, as well as 300 occupational employment and mean wage replicate estimates each based on a different bootstrap subsample. The variance estimates for the occupational estimates based on the full sample are calculated by finding the variability across the occupational replicate estimates. The bootstrap variance estimates are calculated as follows:
![]()
where
![]() occupational estimate (employment or mean wage) for occupation j, within estimation domain D, based on full sample
occupational estimate (employment or mean wage) for occupation j, within estimation domain D, based on full sample
![]() occupational replicate estimates (employment or mean wage) for occupation j, within estimation domain D, based on the bootstrap subsample for replicate b
occupational replicate estimates (employment or mean wage) for occupation j, within estimation domain D, based on the bootstrap subsample for replicate b
1 There is not technically an upper bound on the number of donors. If several donors have the same score, they will all be used, which may put the total number of donors at more than 10. For example, if there are 15 donors with the 10th highest score, all will be used, resulting in a total of 24 donors. Explanations in this section will assume 10 donors, which is the typical number. However, if 10 donors cannot be found, a minimum of 5 donors can be used.
2 The wage interval is indexed by p for each of the six panels. Indexing is done for occupation-specific employment and area-specific employment individually, as well as employment in the aggregate occupation-area.
3 There are 12 wage intervals, but each wage interval is not necessarily assigned an aggregate occupation.