What are contributions and effects? : U.S. Bureau of Labor Statistics

An official website of the United States government

The .gov means it's official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Bureau of Labor Statistics > Consumer Price Index > Publications > Factsheets

What are contributions and effects?

The effect of the change in one index on the change in a broader index and the contribution of the change in one index to the change in a broader index are two ways to measure the impact of the movement of that index on the all items index (or another index of which the first index is a component).

The 'effect' of an item category is a measure of that item's share of the all items price change. For example, if the food index had an effect of 0.4, and the all items index rose 1.2 percent, then the increase in food prices accounted for 0.4 of that 1.2 percent all items increase. Said another way, had food prices been unchanged for that month the change in the all items index would have been 1.2 percent minus 0.4, or 0.8 percent. One-month effects are available in news release table 6, and 12-month effects are available in news release table 7. These tables can be accessed on the archived CPI supplemental files page.

The ‘contribution’ of an item category is another measure of the impact of that item category’s price change on all items price change. The contribution is the item’s effect expressed in percentage terms. So, if the effect of the food index was 0.4 and the all items index increased 1.2 percent in the same period, then the contribution of the food index would be 0.4/1.2 = 33.3%, or one third.

Contributions and effects can be negative as well. For example, if the effect of food was a negative 0.1, and the all items index rose 0.5 percent, the all items index actually would have been 0.1 percent higher (or 0.6 percent) had food prices been unchanged. Since food prices fell while prices overall were rising, the contribution of food to the all items price change was negative (in this case, -0.1/0.5 = -20%).

Note that contributions and effects are calculated from unrounded index changes rather than the published, rounded values.

Calculating contributions and effects

With the addition of data on cost weights to the Consumer Price Index (CPI) website, it is now possible for users of CPI data to calculate contributions and effects for the first time.

A cost weight is an estimated spending total where the price and quantity reference period is different. For example, December 2023 cost weight estimates expenditure totals using prices from December 2023 and quantities from an earlier time period (either 2021 or 2022).

Cost weights are posted for each weight update, referred to as a pivot month. For any month between two pivot months, the cost weight can be found by ‘chaining’ the movement of the related index onto the weight. The formula for a cost weight is given by:

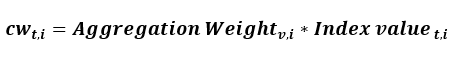
where cw_t,i is the cost weight of item i in month t, and is equal to the product of the pivot-month aggregation weight for item i and the value of the index for item i in month t. It follows algebraically that the aggregation weight can be found by dividing the cost weight by the index value, and so it is possible to convert between the two as needed. As an example, how to calculate the cost weight of rent for July and August 2024 is presented in table 2.

Table 1: Calculating aggregation weight
Item	Cost weight, December 2023	Index value, December 2023	Aggregation weight, December 2023
Rent	701,842,803,000	410.606	1,709,285,308
All items	9,149,300,000,000	306.746	29,826,957,809

Table 2: Calculating cost weight
Month	Index value, Rent	Aggregation weight, Rent, December 2023	Cost weight, Rent
July 2024	420.577	1,709,285,308	718,886,086,802
August 2024	422.223	1,709,285,308	721,699,570,418

Note: The cost weight for all items is rounded to the nearest hundred million dollars, so that the indexes calculated using these weights will be similar in precision to our officially produced indexes (which are rounded to three decimal places). It is important to mention that due to the rounded nature of the weight data provided, such calculations may not exactly match those shown in the CPI news release tables.

Effects

In general, the effect of item i at the US-city average level on the all items index (SA0) at the US-city average level over the period from month t-n to month t is given by:

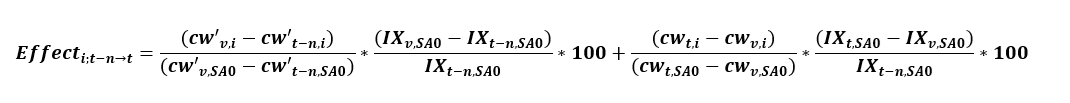
where cw’ is the cost weight calculated using the aggregation weights in effect in month t-n, v is the pivot month (between months t-n and t) when new weights were introduced, and cw is the cost weight calculated using the new aggregation weight introduced in pivot month v and still in use in month t. IX represents index values for the given item category and month. This is, essentially, the sum of the effect from month t-n to the pivot month and the effect from the pivot month to month t. In cases where both t-n and t are months within the same annual weight update period, this formula can be simplified to:

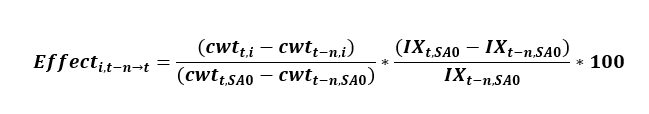
As an example, consider the effect of the U.S. city average rent index on the U.S. city average all items index over the 1-month period from July 2024 to August 2024. This is presented in table 3 below.

Table 3: Calculating 1-month effect
Month	Cost weight, rent	Cost weight, SA0	Index level, SA0
July 2024	718,886,086,802	9,381,771,309,161	314.540
August 2024	721,699,570,418	9,389,407,010,360	314.796
Difference:	2,813,483,616	7,635,701,199	0.256
Ratio:		0.368464342	0.000813887
Product:			0.000299888
x100:			0.029988832

Contributions

In general, the contribution of item i at the US-city average level to the all items index (SA0) at the US-city average level over the period from month t-n to month t is given by:

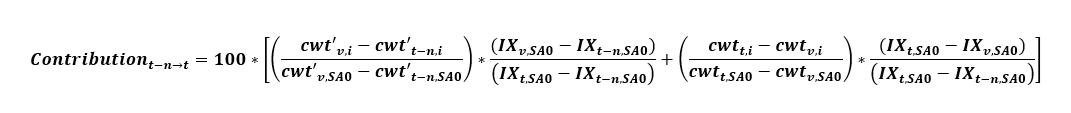
where cw’ is the cost weight calculated using the aggregation weights in effect in month t-n, v is the pivot month (between months t-n and t) when new weights were introduced, and cw is the cost weight calculated using the new aggregation weight introduced in pivot month v and still in use in month t. IX represents index values for the given item category and month. Just as with the effect, this formula can be simplified in the cases where both t-n and t are months within the same annual weight update period:

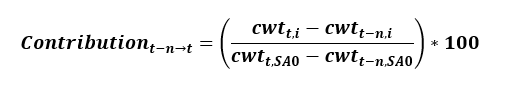
As an example, the calculation of the contribution of the U.S. city average rent index to the U.S. city average all items index between July 2024 and August 2024 is given in table 4:

Table 4: Calculating 1-month contributions
Month	Cost weight, rent	Cost weight, SA0
July 2024	718,886,086,802	9,381,771,309,161
August 2024	721,699,570,418	9,389,407,010,360
Difference	2,813,483,616	7,635,701,199
Ratio		0.368464342
x100 (rounded)		36.85%

Relative Importance

Also available are relative importances which are the ratio of cost weights. The relative importance of a component is its expenditure or value weight expressed as a percentage of all items within an area or an area within the U.S. When the value weights are collected, they represent average annual expenditures, and their relative importance ratios show approximately how the index population distributes expenditures among the components.

For example, the relative importance of item category i to the all items index is given by:

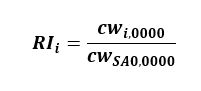
where RI_i is the relative importance of item i at the US-city average level, CW_i,0000is the cost weight of item i at the US-city average level, and CW_SA0,0000 is the cost weight of all items (SA0) at the US-city average level.

Between annual updates based on new consumer expenditure data, relative importances change from month to month as relative prices change. Relative importance ratios cannot be used as estimates of current spending patterns or as indicators of changing consumer expenditures in the intervals between weight revisions because consumption patterns are influenced by factors other than price change. These factors include income, variations in climate, family size, and availability of new and different kinds of goods and services.

Cost weights or relative importance ratios of components in the national or local area Consumer Price Indexes can also be used in the construction of indexes for special combinations of items.

Last Modified Date: May 16, 2025