JOLTS State Estimates Methodology

• Composite Regional Model
• Synthetic Model
• Composite Synthetic Model
• Extended Composite Synthetic Model
• Winsorization
• Seasonal adjustment
• Sample allocation
• Reliability of estimates

The JOLTS sample of 21,000 establishments does not directly support the production of sample based state estimates. However, state estimates have been produced by combining the available sample with model-based estimates. As of October 2021, JOLTS state-level estimates will be made available in an official monthly release approximately two weeks after the JOLTS national release. BLS invites data users to comment on both the methodology used to produce these estimates and on the usefulness of these data.

These estimates consist of four major estimating models; the Composite Regional model (an unpublished intermediate model), the Synthetic model (an unpublished intermediate model), the Composite Synthetic model (published historical series through the most current benchmark year), and the Extended Composite Synthetic model (published current-year monthly series). The Composite Regional model uses JOLTS microdata, JOLTS regional published estimates, and Current Employment Statistics (CES) employment data. The Composite Synthetic model uses JOLTS microdata and Synthetic model estimates derived from monthly employment changes in microdata from the Quarterly Census of Employment and Wages (QCEW), and JOLTS published regional data. The Extended Composite Synthetic extends the Composite Synthetic estimates by ratio-adjusting the Composite Synthetic by the ratio of the current Composite Regional model estimate to the Composite Regional model estimate from one year ago.

The Extended Composite Synthetic model (and its major component—the Composite Regional model) is used to extend the Composite Synthetic estimates because all of the inputs required by this model are available at the time monthly estimate are produced. In contrast, the Composite Synthetic model (and its major component—the Synthetic model) can only be produced when the latest QCEW data are available. The plan is to use Extended Composite Synthetic model estimates to extend the Composite Synthetic model estimates during the annual JOLTS re-tabulation process. The extension of the Composite Synthetic model using current data-based Composite Regional model estimates will ensure that the Composite Synthetic model estimates reflect current economic trends.

The following outlines each model in a non-technical summary format. Each model is summarized separately, and answers the following:

• What is the approach attempting to do?
• What data inputs are used in the approach?
• How does the approach attempt to use that data?
• What data outputs are produced by the approach?
• What limitations does the approach have?
• What more needs to be done?

Composite Regional Model

What Approach?

The Composite Regional approach calculates state-level JOLTS estimates from JOLTS microdata using sample weights, and the adjustments for non-response (NRAF). The Composite Regional estimate is then benchmarked to CES state-supersector employment to produce state-supersector estimates. The JOLTS sample, by itself, cannot ensure a reasonably sized sample for each state-supersector cell. The small JOLTS sample results in quite a number of state-supersector cells that lack enough data to produce a reasonable estimate. To overcome this issue, the state-level estimates derived directly from the JOLTS sample are augmented using JOLTS regional estimates when the number of respondents is low (that is, less than 30). This approach is known as a composite estimate which leverages the small JOLTS sample to the greatest extent possible and supplements that with a model-based estimate. Previous research has found that regional industry estimates are a good proxy at finer levels of geographical detail. That is, one can make a good prediction of JOLTS estimates at the regional-level using only national industry-level JOLTS rates. The assumption in this approach is that one can make a good prediction of JOLTS estimates at the state-level using only regional industry-level JOLTS rates.

In this approach, the JOLTS microdata-based estimate is used, without model augmentation, in all state-supersector cells that have 30 or more respondents. The JOLTS regional estimate will be used, without a sample-based component, in all state-supersector cells that have fewer than five respondents. In all state-supersector cells with 5–30 respondents an estimate is calculated that is a composition of a weighted estimate of the microdata-based estimate and a weighted estimate of the JOLTS regional estimate. The weight assigned to the JOLTS data in those cells is proportional the number of JOLTS respondents in the cell (weight=n∕30, where n is the number of respondents).

What data inputs?

• All JOLTS microdata records
• All weights from JOLTS estimation (final weights that account for sampling weight, NRAF, agg-codes, etc.)
• JOLTS published regional rates estimates (regional JO, H, Q, LD, and TS rates)
• CES state-supersector employment

How are data used?

1. All JOLTS microdata are weighted using final weights. A weighted estimate is made for each JOLTS respondent.
2. Counts are made for each state-supersector cell.
3. Each JOLTS respondent is paired with its regional rate estimate for all variables.
4. Based on the count of respondents in the state-supersector cell the JOLTS respondent belongs to, a Composite Model Weight (CMW) is calculated.
1. If the count is>30, then the CMW for the respondent data=1. The CMW for the regional estimate=0.
2. If the count<5, then the CMW for the respondent data=0. The CMW for the regional estimate=1.
3. If the count is 5–30, then the CMW for the respondent data=n∕30, where n is the number of respondents. The CMW for the regional estimate=1-n∕30.
5. The state-level rate estimate is therefore the final weighted respondent-based JOLTS rate times the CMW added to the regional rate times the CMW, benchmarked to CES state-level estimate:
1. FINAL ESTIMATE=CES STATE EMP×(final weight JOLTS rate×CMW+(regional rate×CMW))
2. The Composite Regional supersector estimates are summed across state industry supersectors to the nonfarm level.
6. To stabilize the estimate, the sum of state Composite Regional estimates within each region is then benchmarked to the published JOLTS regional estimates.

How are outputs produced?

• This model produces state-level estimates of JO, H, Q, LD, and TS. These estimates provide estimates for the most current month of estimates and can be produced during monthly JOLTS estimation production.

What are the limitations?

• JOLTS data are somewhat volatile at the national and regional levels due to the small sample size which in turn results in volatile state estimates.
• The Composite Regional estimates can vary substantially from Composite Synthetic estimates for states that exhibit seasonal employment patterns that differ substantially from the JOLTS region to which they belong. For example, Alaska has a pronounced seasonal employment pattern that differs from the West region in which it resides. Consequently, the Composite Regional estimates derived using West region JOLTS rates substantially understate the JOLTS rates in that state.

What more is needed?

These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which will be updated annually in July.

Synthetic Model

What approach?

The Synthetic model differs fundamentally from the Composite Regional model. The Synthetic approach does not use JOLTS microdata but rather it uses data from the QCEW that have been linked longitudinally (Longitudinal Database—LDB), the QCEW-LDB. The Synthetic model attempts to convert QCEW-LDB monthly employment change microdata into JOLTS job openings, hires, quits, layoffs and discharges, and total separations data.

What data inputs?

• All monthly employment changes for each record on the QCEW-LDB
• JOLTS published regional estimates (regional JO, H, Q, LD, and TS)

How are data used?

1. Every record on the QCEW-LDB is classified as expanding, contracting, or stable based on monthly employment change.
1. For expanding records, the amount of employment growth is converted to JOLTS hires. They are given no separations.
2. For contracting records, the amount of employment decline is converted to JOLTS separations. They are given no hires.
3. For stable records, no attribution of JOLTS hires or separations is made.
2. The entire QCEW-LDB is summarized to the US Census regional level.
3. The QCEW-LDB regional summary is ratio adjusted to the JOLTS published regional estimate for hires and total separations.
1. For each region, the ratio of QCEW-LDB based regional hires and total separations to JOLTS published hires and total separations is calculated (Ratio-H for hires and Ratio-TS for total separations).
2. Each record on the QCEW-LDB within each US Census region will have their converted JOLTS data multiplied by Ratio-H and Ratio-TS, by region.
3. 1. For expanding records, the amount of employment growth is then: (JOLTS hires×Ratio-H). They remain with no separations.
   2. For contracting records, the amount of employment decline is then: (JOLTS separations×Ratio-TS). They remain with no hires.
   3. For stable records, they remain with no JOLTS hires or separations.
4. To produce state-level estimates, sum the regional hires×Ratio-H by state to produce a state-level JOLTS hires estimate and sum the TS×Ratio-TS by state to produce a state-level JOLTS total separations estimate.

How are the outputs produced?

• State-level JOLTS estimates for hires and total separations come directly from the model outlined above.
• • Synthetic job openings are a function of the ratio of industry-regional job openings and hires. This ratio of published job openings to hires is applied to model hires estimates to derive model job opening estimates. Ratio-adjusting the JOLTS model hires and separations to the regional published JOLTS hires and separations estimates ensures that the JOLTS published churn rate is fully accounted for.
  • • 
  • Synthetic quits and layoffs and discharges are a function of the relative percentage of the individual components of total separations at the industry-regional level. The relative percentages of each component are applied to the model separations estimates to derive model quits and layoffs and discharges.
  • • 
    • 
    • 
    • 

What are the limitations?

• This approach is NOT meant to model individual QCEW-LDB data records. It would not be prudent to use this approach to model small populations (30 or fewer establishments). The model works best at the state-level, and while it is possible to model smaller populations, there potentially is a reduction in the strength of the model proportionate to the reduction in the size of the population being modeled
• The model does generate state-level job openings and separations breakouts. However, these estimates are based upon ratios that are common across the region to which a state belongs. If there are significant differences in the ratio of job openings to hires or separations breakouts for any particular state (or set of states) within a region, the model cannot detect that and estimates will not reflect those differences.
• Since the model is based on QCEW-LDB data, the model cannot produce current state-level estimate since QCEW-LDB data lags current JOLTS estimation production by 6–9 months.

What more is needed?

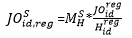
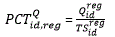
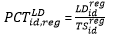
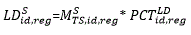
These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which will be updated annually in July.

Composite Synthetic Model

What approach?

The Composite Synthetic model is nearly identical to the Composite Regional model. The primary difference is the use of the Synthetic model estimates (described in the first section) rather than JOLTS published regional estimates when there is an insufficient amount of JOLTS microdata to produce a state-supersector estimate.

Just like the Composite Regional approach, the JOLTS microdata-based estimate is used in all state-supersector cells that have 30 or more respondents. However, in contrast to the Composite Regional approach, the Composite Synthetic approach uses the Synthetic estimate in all state-supersector cells that have fewer than five respondents. In all state-supersector cells with 5–30 respondents an estimate is calculated that is a composition of a weighted estimate of the microdata-based estimate and a weighted estimate of the Synthetic estimate. The weight assigned to the JOLTS data in those cells is proportional the number of JOLTS respondents in the cell (weight=n∕30, where n is the number of respondents).

The Composite Synthetic supersector estimates are summed across state-supersectors to the nonfarm level.

What data inputs?

• All JOLTS microdata records
• All weights from JOLTS estimation (final weights that account for sampling weight, NRAF, agg-codes, etc.)
• Synthetic estimates (regional JO, H, Q, LD, and TS rates)
• JOLTS regional-level estimates (to benchmark the state estimates)
• CES state-supersector employment

How are data used?

1. All JOLTS microdata are weighted using final weights. A weighted estimate is made for each JOLTS respondent.
2. Counts are made for each state-supersector cell.
3. Each JOLTS respondent is paired with its Synthetic rate estimate for all variables.
4. Based on the count of respondents in the state-supersector cell the JOLTS respondent belongs to, a Composite Model Weighted (CMW) estimate is calculated.
1. If the count is>30, then the CMW for the respondent data=1. The CMW for the Synthetic estimate=0.
2. If the count<5, then the CMW for the respondent data=0. The CMW for the Synthetic estimate=1.
3. If the count is 5–30, then the CMW for the respondent data=n∕30, where n is the number of respondents. The CMW for the Synthetic estimate=1−n∕30.
5. The state-level rate estimate is therefore the final weighted respondent-based JOLTS rate times the CMW added to the Synthetic rate times the CMW, benchmarked to CES state-level estimate:
1. FINAL ESTIMATE=CES STATE EMP×((final weight JOLTS rate×CMW)+(synthetic rate×CMW))
6. To stabilize the estimate, the sum of state Composite Synthetic estimates within each region is then benchmarked to the published JOLTS regional estimates.

How are outputs produced, and what are the limitations?

• This model produces state-level estimates of JO, H, Q, LD, and TS. These estimates cannot be produced without lag.

What more is needed?

These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which will be updated annually in July.

Extended Composite Synthetic Model

What Approach?

The Extended Composite Synthetic model is designed to project the Composite Synthetic forward until QCEW-LDB data are available to produce Composite Synthetic estimates. The Composite Synthetic estimates are extended using the ratio of the current Composite Regional state industry estimate to the Composite Regional state industry estimate from one year ago.

This approach ensures that the Extended Composite Synthetic state estimates reflect current JOLTS regional and industry-level economic conditions. The Extended Composite Synthetic estimates reflects current JOLTS state economic conditions to the extent that sufficient JOLTS microdata are available.

What data inputs?

• The historical series of Composite Synthetic model estimates at the state-industry-level
• The historical series of Composite Regional model estimates at the state-industry-level

How are data used?

The Composite Synthetic model estimates are produced at a lag since QCEW-LDB data are only available at a 6–9 month lag relative to JOLTS data. The Composite Regional model estimates, in contrast, are not produced at a lag and are available concurrent with JOLTS data. Therefore, Composite Synthetic estimates can be extended by ratio-adjusting the Composite Synthetic estimates by the ratio of current Composite Regional estimates to the Composite Regional estimates from one year ago at the state-industry-level as follows:

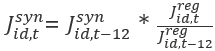
Where

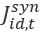• is the Extended Composite Synthetic state industry estimate for month t
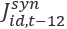• is the Composite Synthetic state industry estimate for month t-12 (one year ago)
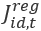• is the Composite Regional state industry estimate for month t
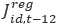• is the Composite Regional state industry estimate for month t-12 (one year ago)

State-level estimates are produced by summing the Extended Composite Synthetic estimates over industry.

How are outputs produced, and what are the limitations?

• This model will produce state-level estimates of JO, H, Q, LD, and TS. These estimates are produced without lag. The methodology allows the Extended Composite Synthetic data to reflect current economic trends at the CESID Industry-Region level. The projection reflects current state economic trends where sufficient JOLTS microdata are available.

What more is needed?

These estimates are based upon a model. BLS constructed a methodology to produce error measures of estimates, which will be updated annually in July.

Winsorization

What is winsorization and how is it used for state estimates?

Winsorization is a process used to safeguard against extreme values or outliers that potentially could unduly impact a forecasted estimate. The technique for JOLTS state estimates involves identifying monthly outliers by state and data element and replacing them with winsorized values. Although unusually high values are rare, having safeguards against extreme values will lessen the impact of these anomalies and reduce the volatility in JOLTS State estimates.

Procedure:

The JOLTS State Estimates are based on a composite model of QCEW data and JOLTS reported data. However, while current JOLTS reported data are available at the time of production, current QCEW data are not. Consequently, JOLTS State estimates are forecasted using the previous year’s QCEW estimate and JOLTS regional rates. By definition, the year-ago QCEW estimate is multiplied by the ratio of the current Regional estimate to the year-ago Regional estimate at the State/CES ID level:

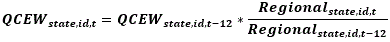
The ratio of the current Regional estimate to the year-ago Regional estimate at the State/CES ID level 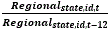is winsorized. The winsorization cutoffs are the historical 99th percentile of regional ratios for each variable (job openings, hires, quits, layoffs and discharges, and other separations). Even though other separations are not published for state estimates it is still identified in the winsorization process as it is one of the components to total separations.

Please visit the state-level estimation section of JOLTS Handbook of Methods for detailed information on the JOLTS state methodology.

Seasonal Adjustment

Most series published by the Job Opening and Labor Turnover Survey (JOLTS) program have a regularly recurring seasonal movement that can be measured from past data. Seasonal adjustment eliminates the component of the change attributable to the normal seasonal variation and makes it possible to observe the cyclical and other nonseasonal component movements in the series. Seasonally adjusted series are published monthly for JOLTS estimates. The JOLTS program uses X-13-ARIMA-SEATS software developed by the U.S. Census Bureau to seasonally adjust the monthly estimates. The X-13-ARIMA-SEATS software is available on the U.S. Census Bureau website. The JOLTS program employs a concurrent seasonal adjustment methodology to seasonally adjust its estimates. Under concurrent methodology, new seasonal factors are calculated each month using all relevant data up to and including the current month period.

Seasonal adjustment input files

All controllable variables remain fixed during the year. For example, the ARIMA model, outliers, transformation specification, and historical data are held constant. Once a year, as part of the annual JOLTS benchmark procedure, all seasonal adjustment specifications are reviewed for each series. Any changes are implemented and kept constant until the next annual benchmark. Also during the annual benchmark, estimates for the 5 most recent years are readjusted using the new specifications. Estimates are only revised back for a 5-year period.

Additive and multiplicative models

The model specifications provide the mode (additive or multiplicative) selected for each JOLTS series by state. Depending on the relationship between the original series and each of the components, the mode of seasonal adjustment may be additive or multiplicative. Formal tests are conducted to determine the appropriate mode of adjustment.

The multiplicative mode assumes that the magnitude of the seasonal pattern is proportional to the level, which implies that the size of the seasonal fluctuations increases and decreases with the level of the series. With this mode, the monthly seasonal factors are ratios, with all positive values centered around one. The seasonally adjusted values are computed by dividing each month's original value by the corresponding seasonal factor.

In contrast, the additive mode assumes that the magnitude of the seasonal pattern is independent of the level of the series. In this case, the seasonal factors represent positive or negative deviations from the original series and are centered around zero. The seasonally adjusted values are computed by subtracting the corresponding seasonal factor from each month's original value.

Regional raking procedure

A raking procedure is used to ensure that the sum of the seasonally adjusted state series is consistent with the published seasonally adjusted total at the regional levels. The raking procedure begins by seasonally adjusting the regional and state level series independently. The seasonally adjusted state series are summed to the regional levels to get the regional totals. Ratios of seasonally adjusted state-to-regional levels are calculated. The regional totals summarized from the seasonally adjusted state series are subtracted from the official regional seasonally adjusted estimates to determine the amount that must be raked. The total amount that must be raked is multiplied by the ratios to determine what percentage of the raked amount should be applied to each state. Once the seasonally adjusted state series receive their proportional amount of the raked values, the two groups are aggregated again to regional totals. At this point their sum should be equal to the official regional seasonally adjusted estimate.

Sample Allocation

What is the sample size allocation for the inputs used to produce the JOLTS state estimates?

The JOLTS state estimates sample allocation table below provides a snapshot of the sample used to produce December 2022 and December 2023 state estimates. Sample are utilized in both components of the model. The sample component incorporates JOLTS state respondent data. The model component incorporates JOLTS regional-level respondent data, CES state respondent data, and QCEW establishment counts.

Reliability of Estimates

What is the reliability of the JOLTS state estimates?

JOLTS state estimates are subject to both sampling and nonsampling error. Sampling error occurs when a sample is surveyed rather than the entire population. There is a chance that the sample estimates may differ from the true population values they represent. The difference, or sampling error, varies depending on the particular sample selected. This variability is measured by the standard error of the estimate. BLS analysis is generally conducted at the 90-percent level of confidence. That means that there is a 90-percent chance, or level of confidence, that an estimate based on a sample will differ by no more than 1.6 standard errors from the true population value because of sampling error.

The JOLTS state estimates also are affected by nonsampling error. Nonsampling error can occur for many reasons including: the failure to include a segment of the population; the inability to obtain data from all units in the sample; the inability or unwillingness of respondents to provide data on a timely basis; mistakes made by respondents; errors made in the collection or processing of the data; and errors from the employment benchmark data used in estimation.

The JOLTS State variance estimates account for both sampling error and the error attributable to modeling. A small area domain model uses a Bayesian model to develop estimates of JOLTS State variance. The small area model uses QCEW-based JOLTS synthetic model data to generate a Bayesian prior distribution, then updates the prior distribution using JOLTS microdata and sample-based variance estimates at the State and US Census Regional level to generate a Bayesian posterior distribution. Once the Bayesian posterior distribution has been generated, an estimate of JOLTS State variance estimates is made by drawing 2,500 estimates from the Bayesian posterior distribution. This Bayesian approach thus indirectly accounts for sampling error and directly for model error. The median standard errors table by state is available on the JOLTS Median Standard Errors page. The error measures will be updated annually in July.

Last Modified Date: July 24, 2024