Handbook of Methods Productivity Measures: Business Sector and Major Subsectors Calculation

Productivity statistics describe how efficiently an industry or sector produces goods and services. Measures of productivity are calculated by independently calculating inputs and outputs. A change in the quantity of output that is not explained by an equivalent change in inputs is defined as growth (or decline) in productivity. The following section will describe the mathematical principles and techniques by which industry output, inputs, and productivity series are measured.

Labor productivity, or output per hour, is computed as an index of real output divided by an index of hours worked:

 1 Labor productivity= Output index Hours worked

Multifactor productivity (MFP) is computed as an index of real output divided by an index of combined inputs used to produce that output. Inputs can include labor, capital, energy, materials, and purchased services.

2 MFP= Output index Combined inputs

Output

Real business sector output is an annual-weighted (Fisher-Ideal) index constructed by the Bureau of Economic Analysis (BEA) from the gross domestic product (GDP) excluding the following outputs: general government, nonprofit institutions, paid employees of private households, and the rental value of owner-occupied dwellings. This measure, and the measure of nonfarm business sector output, which also excludes farm output, are the real output series used to calculate Bureau of Labor Statistics (BLS) measures of labor productivity in the U.S. business and nonfarm business sectors, using both quarterly and annual BEA output data. To measure multifactor productivity, BLS further restricts output to the U.S. private business and private nonfarm business sectors, which exclude the output of government enterprises. BLS multifactor productivity statistics for the private business and private nonfarm business sectors are constructed using annual BEA output data.

Annual manufacturing output indexes for both labor productivity and multifactor productivity measures are constructed by deflating the current-dollar industry value of production published by the U.S. Bureau of the Census along with data published by BEA. Industry shipment data are converted to a current dollar production basis by adjusting for the inventory and resale values. These data are converted to a sectoral output basis by removing the intra-industry transactions. The output index for manufacturing is constructed using a chained superlative index (Törnqvist) of three-digit North American Industry Classification System (NAICS) industry outputs. This index formula aggregates the growth rates of detailed primary and secondary industry outputs between two periods, using their relative shares in industry value of production averaged over the two periods as weights.

Quarterly indexes of manufacturing output underlying the quarterly labor productivity data are estimated using the annual manufacturing indexes and monthly Indexes of Industrial Production, prepared by the Board of Governors of the Federal Reserve System (FRB). To derive quarterly estimates from the annual manufacturing indexes, a quarterly reference series, constructed from the FRB indexes, is adjusted to the annual totals using a quadratic minimization formula devised by Frank Denton.^⁠1 Because of a lag in the availability of the annual benchmark data, recent quarterly and annual manufacturing output measures also are extrapolated based on the changes in the Indexes of Industrial Production.

Labor hours

For labor productivity, real output is compared to the number of hours worked in a sector. Total quarterly and annual hours worked are estimated separately for three categories: paid employees, self-employed, and unpaid family workers. Employees account for about 90 percent of hours worked. Seasonally adjusted monthly data on employment and average weekly hours of all employees, and of production and nonsupervisory employees only, are provided by the BLS Current Employment Statistics (CES) program for 83 three-digit-level NAICS industries in the private nonfarm sector. Employment of nonproduction or supervisory workers in each industry is found by subtracting employment of production workers from employment of all employees.

CES average weekly hours are collected on an hours-paid basis, including time when employees are not at work. Therefore, ratios of hours worked to hours paid by three-digit NAICS industry from the BLS National Compensation Survey (NCS) are applied to the average weekly hours of production workers. This adjustment ensures that changes in vacation, holiday, and sick pay do not affect growth in hours. More formally, hours worked by production workers and nonsupervisory (P) workers are given by:^⁠2

3 Hours worked P = AWH P CES × hwhp NCS × Emp P CES × 52

where,

Hours worked P = hours worked by production workers

AWH P CES        = average weekly hours of production workers from the CES

hwhp NCS         = hours worked to hours paid ratio from the NCS

Emp P CES           = production worker employment from CES

52                    = weeks in the year used to get an annualized value

For supervisory workers, ratios of average weekly hours worked by supervisors to average weekly hours worked by production workers at the 14-sector level are derived from data on hours worked collected by the Current Population Survey (CPS). These ratios are applied to the average weekly hours worked by production workers after they have been aggregated to a 14-sector level to estimate average weekly hours worked by supervisory workers. For each sector, the hours of non-production and supervisory workers (S) are calculated as follows:

4 Hours worked S = ( AWH P CES × hwhp NCS ) × AWH S CPS AWH P CPS × Employment S CES × 52

Hours worked for the two worker groups (equations 3 and 4) are summed to all-employee hours for each of the fourteen sectors, then aggregated to private nonfarm employee hours worked.

To measure the business sector, the private nonfarm hours worked series must be further adjusted to exclude nonprofit institutions. The Economic Census is published every 5 years and provides employment by tax status of the employer. The BLS Office of Productivity and Technology (OPT) uses tax-exempt status as a proxy for nonprofit status. To exclude nonprofit employee hours, ratios of tax-exempt employment to total employment (from the Economic Census) are calculated at the three-digit level. For some industries these ratios are estimated using BEA data on compensation of employees by tax status.

5 nonprofit i = (Tax exempt employment) i (Taxable employment + Tax exempt employment) i

Employment and hours worked of production workers in each 3-digit industry are multiplied by the nonprofit ratio:

6 Hours worked P Business = ∑ i Hours worked P,i × (1 - nonprofit i )

7 Employment P Business = ∑ i Employment P,i × (1 - nonprofit i )

where,

i = three-digit level industry.

After the production worker data are aggregated to the 14-sector level, average weekly hours for production workers in the business sector, AWH P Business, are derived as the ratio of hours divided by employment. Supervisory worker hours in the business sector can then be calculated as follows:

8 Hours worked S Business = ( AWH P Business × hwhp NCS ) × AWH S CPS AWH P CPS × Emp S CES × 52

Again, hours worked by the two worker groups are summed to obtain hours worked by employees excluding employees of nonprofit institutions by sector, then aggregated to yield hours worked in private nonfarm business sector:

9 Hours worked all Business = ∑ j ( Hours worked P Business + Hours worked S Business ) j

where,

j = 14-sector level sector.

For the nonfinancial corporate sector, noncorporate and financial employees are excluded in addition to employees of nonprofit institutions. Employees in the financial industries are simply excluded from the aggregation. Estimating corporate employee hours is similar to the approach used for nonprofits; corporate employment ratios are calculated by dividing corporate employment by total employment from data reported by the Economic Census. These ratios are applied to both production and supervisory employee hours worked at the three-digit industry level, then the adjusted measures are aggregated to nonfinancial corporate sector hours.

Hours worked by employees of government enterprises must be estimated, and added to private nonfarm business employee hours, to yield hours worked by all employees in the nonfarm business sector. Annual employment in federal, and state and local, government enterprises from the National Income and Products Account (NIPA) is combined with monthly data from the CES on federal, state, and local employment, and from the CPS on average weekly hours of related workers—federal postal workers and state and local public administration workers excluding education—to estimate hours of these employees.

Employee hours worked must be supplemented with hours worked by self-employed and unpaid family workers to yield measures of hours worked by all persons in the published sectors. The CPS provides hours worked by the self-employed and unpaid family workers in both the nonfarm and farm sectors, and by farm employees.^⁠3

Seasonal adjustment

All uses of monthly CPS data start from not-seasonally-adjusted data, which are seasonally adjusted by OPT. The Census X-12-ARIMA Seasonal Adjustment Program Method is used to create monthly and quarterly seasonally adjusted data. The X-12 method modifies the X-11 variant of the Census Method. Currently, 4 of the 17 CPS source data series are not seasonally adjusted because they exhibit no identifiable seasonal pattern. OPT employs concurrent seasonal adjustment of CPS-based measures, and revises two prior months of data each time a new month of data is added. This mirrors the BLS practice of revising two prior months of CES data on employment and average weekly hours of employees each month. Each January, when another year of monthly or quarterly data is completed, each series is analyzed to identify the best seasonal adjustment parameters. These parameters are then locked in for the coming calendar year. Seasonally adjusted CPS data are not revised for prior years. Seasonally adjusted monthly CPS data are averaged to get quarterly and annual measures of hours worked by self-employed and unpaid family workers. Hours of these workers are added to the hours worked by paid employees to obtain hours worked by all persons in each of the industries or major sectors for which BLS measures and publishes productivity.

Labor input

Labor input is an aggregation of hours worked by different types of workers with different skills and experience. BLS computes this as a measure of hours worked adjusted by a labor composition index which weights the heterogeneous class of workers by their median wage.^⁠4

(10) Δ LN( labor input) t = Δ LN( labor composition) t + Δ LN( Hours worked) t

This adjustment is part of the calculation of multifactor productivity. BLS computes the labor composition using data from the CPS that are scaled to published CES estimates.

BLS partitions workers into 70 different categories depending on a worker’s age, gender, and level of education. There are seven age categories, five education categories, and two gender categories. (See exhibit 1.)

BLS uses age, gender, and education levels as proxies for experience and ability. Age is used as a proxy to measure years of potential experience, in that workers, in a given age × education cell will have similar levels of potential labor market experience.^⁠5 Male and female designations are included as a stratifying variable to account for the differential returns to potential experience and for the different occupational choices of men and women (which could be the result of preferences or discrimination).^⁠6

Individuals in age group 1 with a college degree or higher are a special case because there are very few 16- to 18-year-olds with a college degree or higher. These workers are promoted to the 19- to 24-year-olds group 2.

The sample includes all employed persons who worked during the reference week and were classified as in-scope. Those who were employed but did not work during the reference week are included when estimating wages but not when aggregating hours.

To measure the growth in hours worked, BLS uses actual hours worked during the previous week. For each demographic cell, total annual hours are calculated as follows:

11 Annual Hours CPS = Average Monthly Employment CPS * Average Weekly Hours CPS * 52

If an hourly wage is reported to CPS, the hourly wage is used. If an hourly wage is not reported, the hourly wage is calculated as usual weekly earnings divided by usual weekly hours (both on the main job). If usual weekly hours is reported as “hours vary,” actual weekly hours are used.^⁠7 These wages are used to calculate total labor costs and cost-share weights for each cell. The CPS files do not have earnings data for self-employed workers or for second jobs. For labor composition calculations, BLS assumes that these workers earn the same hourly wage as wage and salary workers in the same estimating cell.

Ratio adjustments

Data on industry and hours data for second jobs (for multiple jobholders) is available starting in 1994. Before 1994, hours on both jobs were reported together, and all hours were attributed to the first job’s industry. For these years, BLS calculates a ratio—by industry using 1994 data—that relates hours worked first and second jobs to the hours that would have been attributed to the industry in the pre-1994 data:^⁠8

12 Ratio = 1994 sum of actual hours worked at 1 st ,2 nd jobs in an industry 1994 actual hours worked all jobs attributed to 1 st jo b ' s industry

This ratio is used to reweight individual observations in 1993 and earlier years.

Prior to 1994, it was not possible to distinguish between private employees at for-profit and nonprofit establishments. BLS calculates an industry-level ratio adjustment to remove employees of nonprofits. This ratio is calculated using 1994 data and is applied to the pre-1994 data:

13 Ratio = 1994 total private , for profit , employment in an industry 1994 total private , for profit and nonprofit , employment in an industry

Törnqvist aggregation

BLS uses growth in hours and two-period-average labor-cost shares to calculate a Törnqvist index of labor input. The labor composition adjustment is the difference between the growth in labor input and the growth in total labor hours. To calculate labor composition, the labor cost of a group (both of each cell and the total industry) are estimated:

14 Labor cost = median hourly wage*total annual hours

Cost share weights for the Törnqvist index are calculated for each demographic cell as that cell’s share of total labor cost. In each cell, total labor cost is calculated as the median wage times total hours.^⁠9 Share weights are equal to the cell’s total labor cost divided by aggregate labor cost. The medians are calculated on an hours weighted basis using a modified version of the BLS interval method for calculating median hourly wages, and can be thought of as the wage of the median hour worked.

Next, the annual cost share for all cells within an industry or sector is computed:

15 Annual cost share s j = labor cost of a cell labor cost of an industry

The growth in labor input within an industry or sector is calculated as follows:

(16) Δ ln Labor Input t = ∑ j ∊ J 1 2 s j , t + s j , t - 1 Δ LN( Hours worked) j , t

where,

 s j , ts j,t = Cost share of demographic group j in time t.

Changes in the index of labor composition are defined as the difference between the change in composition-adjusted hours given in (equation 16), and the change in the unadjusted (unweighted) hours of all workers can be shown by rearranging (10):

17 Δ ln Labor composition t = Δ ln Labor input t - Δ ln Hours worked t

The index is calculated by chaining the annual growth rates to the base year.

Note that for a cell to be included in the calculation, it must have a matching cell for the prior year in order to measure growth over time. BLS employs data estimation techniques and multiple imputations to fill in missing observations and where data are too thin to adequately evaluate. The growth rate of the aggregate is therefore a weighted average of the growth rates of each type of worker where the weight assigned to a type of worker is its two-period-average share of total wages. The resulting aggregate measure of labor input accounts for both the increase in raw hours at work and changes in the skill composition (as measured by age and education) of the work force.

Capital input

Capital input, also known as capital services, is estimated by calculating productive capital stocks; capital services are assumed to be proportional to changes in the quantity of capital stocks for each asset. The capital index is a Törnqvist index of separate quantity indexes of equipment, structures, inventories, and land.

Capital stocks are composed of numerous different assets purchased at different times, which fall within the categories of equipment, structures, inventories, or land. The measure of capital stock for each year includes that year’s investment in an asset plus the remaining productive stock from all previous years’ investments. Capital stocks of equipment and structures for each industry are calculated using the perpetual inventory method, which takes into account the continual additions to and subtractions from the stock of capital as new investment and retirement of old capital occur. Real (constant dollar) investments in various assets are estimated by deflating current dollar investments with appropriate price deflators. The perpetual inventory method measures real stocks at the end of a year equal to a weighted sum of all past investments, where the weights are the asset’s efficiency relative to a new asset. A hyperbolic age efficiency function is used to calculate the relative efficiency of an asset at different ages.

The hyperbolic age-efficiency function can be expressed as:

18 Asset efficiency t = Asset service life - t (Asset service life - β t)

where,

t = the age of the asset, and

β = the parameter of efficiency decline.

The service life of the asset for each cohort of each type of equipment and structure is assumed to be normally distributed around an average service life for that asset type. For most assets, these service lives are the same across all industries. The parameter of efficiency decline is assumed to be 0.5 for equipment and 0.75 for structures.^⁠10

These parameters yield a function in which assets lose efficiency more slowly at first, and then lose efficiency more rapidly later in their service lives.

The annual inventory stocks for finished goods, work in process, and materials and supplies are calculated by using a weighted average, including five quarterly inventory numbers.

Various equipment, structure, inventory, and land stock series in constant dollars are aggregated into one capital input measure using a Törnqvist formula. Capital stocks multiplied by implicit rental prices yield cost share weights.

Rental prices are calculated for each asset as:

19 Rental price= P * R + P * D - ∆ p 1 - uz - k / 1 - u

where,

P = deflator the the asset,

R = internal rate of return,

D = rate of depreciation for the asset,

∆p = capital gain term representing the price change of the asset over the prior

three years,

1 - uz - k 1 - u = tax,

u = the corporate tax rate, and 

z= present value of $1 of depreciation deduction = effective investment tax credit rate.

Rental prices are expressed in rates per constant dollar of productive capital stocks. Each rental price is multiplied by its constant-dollar capital stock to obtain asset-specific capital costs, the shares of which are used for Törnqvist aggregation.

The stock of research and development (R&D) in private nonfarm business is obtained by cumulating constant dollar measures of research and development expenditures net of depreciation. BLS develops price deflators and also estimates the rate of depreciation of R&D.^⁠11

Capital intensity is the ratio of capital services to hours worked in the production process. The higher the capital to hours ratio, the more capital intensive the production process becomes.

20 Capital intensity = Capital services Hours worked

Intermediate inputs of production

Intermediate inputs consist of energy, materials, and purchased business services and represent a large share of production costs. Data on intermediate inputs are obtained from BEA based on BEA annual input-output tables. Törnqvist indexes of each of these three input classes are derived at the roughly three-digit NAICS level. Materials inputs are adjusted to exclude transactions between establishments within the same goods producing sector.

Combined inputs of production

BLS aggregates inputs for its multifactor productivity measures using a Törnqvist chain index method. This index is calculated as a weighted average of growth rates of the components; the weights are allowed to vary for each time period; and the weights are defined as the mean of the relative compensation shares of the components in two adjacent years. For example, the index of inputs (I) in each year, t, for major sectors, in which output is value added, is calculated by linking to the previous year’s index:

21 Δ ln Combined inputs t = ∑ j ∊ K,L 1 2 s j , t + s j , t - 1 Δ ln input j , t

where,

= share of input j in time t.^⁠12

Multifactor productivity

For the private business and private nonfarm business where output is measured as value added, the multifactor productivity (MFP) growth can be expressed in the following way:

22 ∆ MFP = ∆ Value added output - s K ∆ K K - s L ∆ L L

where,

s_j = average two period share of costs of input j divided by output,

K = real capital services, and

L = labor input.

Whereas the 60 NAICS industry multifactor productivity uses a sectoral output concept which includes the intermediate inputs of energy, materials, and purchased business services along with the primary inputs of capital and labor input. This can be written in the following way:

23 ∆MFP = ∆Sectoral output - s K ∆K K - s L ∆L L - s E ∆E E - s M ∆M M - s S ∆S S

where,

s_j = average two period share of costs of input j divided by output,

K = Capital input

L = Labor Input- including the effects of both labor composition and hours

E = real energy input,

M = real materials, and

S = real purchased services.

For private business and private nonfarm business, the relationship of aggregate multifactor productivity to aggregate labor productivity can be further explored by the following equation:

24 ∆LN( Output Labor Hrs ) dt = ∆LN(A) dt + s K ∆LN Capital Labor Hrs dt + s L ∆LN(Labor Composition) dt

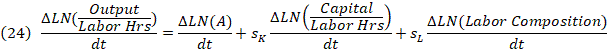
where,

      s_j         = average two period share of costs of input j divided by output,

Capital Labor Hrs= capital intensity = capital input divided by labor hours,

Output Labor Hrs= labor productivity, and

     A      = multifactor productivity.

This equation shows that labor productivity growth is decomposed into multifactor productivity growth, the contribution resulting from K/L substitution (capital deepening) and the contribution of the labor composition effect. Thus, labor productivity grows because of shifts in the production function, A, because of increases in capital intensity, and shifts in the composition of workers.

For industries and NAICS NIPA-level industry, labor productivity growth also results from the contribution resulting from intermediate inputs.

Preliminary multifactor productivity

Measures for the most recent year of the multifactor productivity trends are preliminary. A simplified methodology is used to estimate preliminary multifactor productivity change in the private business and private nonfarm business sectors. The simplified method uses preliminary data to estimate 1 additional year of data past the reference year. The simplified methodology involves making estimates of the growth rates of output, labor input and capital input, and of the shares of each input. Using the same basic structure and assumptions, the simplified methodology is designed to yield estimates of multifactor productivity approximating closely those calculated by the full methodology. The simplified methodology includes fewer categories of capital than the full methodology. The simplified measure is usually based on information from the full calculation from the previous year and on up-to-date information on hours worked from BLS and output and capital from NIPA and other sources available early in the year following the target year. The resulting simplified measure will later be updated when more complete source data become available. In practice, the revision of the simplified estimate to obtain a full estimate reflects both the difference in methodologies and concurrent revisions to the underlying source data.^⁠13

Costs of production

The production function specifies a certain set of output given a certain set of inputs. On a current dollar basis this production equates from paying the factors of production their marginal cost. Below are the costs associated with the value of production.

Labor compensation

Total quarterly and annual labor compensation are estimated separately for two categories: paid employees and self-employed. Detailed measures of current dollar employee compensation come from the BEA national accounts. To construct an estimate of employee compensation for the business sector, BLS subtracts compensation of employees of general government, nonprofit institutions, private households, and compensation paid to foreign residents from total employee compensation. These components are part of the BEA’s estimates of national income. BLS estimates compensation of self-employed workers by assuming their compensation per hour is equal to that of the employees in the same sector. Self-employed compensation is calculated by multiplying the compensation per hour of the paid employees by the hours worked of self-employed. The compensation of the two categories of paid employees and the self-employed are then summed to obtain a total compensation measure.

In the estimation of self-employed compensation for the multifactor productivity program, a similar set of assumptions are made but are then controlled to the BEA income estimates. Noncorporate capital services and noncorporate hours each are assumed to receive the same percentage of corresponding factor returns as elsewhere in the industry.

Capital costs of production

Data are available from BEA for employee compensation and for corporate capital income. Corporate capital income is defined by BLS to include unadjusted before-tax profits, corporate capital consumption allowances, corporate net interest payments, corporate inventory valuation adjustments, and a portion of indirect business taxes. Corporate capital income is used to determine the corporate rental price for each type of asset. However, BEA reports only a single figure for proprietors’ income, which reflects returns to both labor and capital. Since data are available on hours of self-employed, and on noncorporate capital stock, it is possible to develop an implicit capital-labor split of proprietors’ income by assuming either that proprietors earn the same wage as employees or that corporate and noncorporate capital yield the same rate of return.

Unfortunately, the two methods of imputation applied together generally overestimate the NIPA measures of proprietors’ income. Rather than select one imputation over the other, the two methods are initially employed simultaneously, and the results are reconciled to the BEA proprietors income estimate.

First, an imputation is made for noncorporate income by assigning self-employed and unpaid family workers the same average wage received by paid employees, and then adding to that an imputation of capital income by assigning noncorporate capital the same rental price as corporate capital. This imputation is compared to noncorporate income in the NIPA. (Noncorporate income includes proprietors’ income, noncorporate capital consumption allowances, and a portion of indirect business taxes.) The imputation is adjusted to equal the reported noncorporate income by multiplying the wages of self-employed and unpaid family workers and the noncorporate rate of return by a single scalar which equates the imputed and NIPA totals.

Thus, noncorporate wages and the rate of return to capital are scaled back proportionally to determine proprietors’ capital and labor shares. It should be noted that the scalar is applied only to the rate of return on capital, not to the entire rental price. Thus, the noncorporate rates of economic depreciation, asset revaluation, and indirect taxes are held equal to the corporate sector. The rationale for this treatment is that these other elements are exogenous for the self-employed. The self-employed can willingly accept lower wages and returns to their capital in exchange for the greater degree of independence—or for some other reason. However, their preference is unlikely to affect factors like economic depreciation or inflation.

Noncorporate capital services and noncorporate hours each are assumed to receive the same percentage of corresponding factor returns as elsewhere in the industry. Thus, the noncorporate rate of return and proprietors’ (self-employed) compensation per hour are compared to the corporate rate of return and employees compensation per hour respectively. For example, if the noncorporate rate of return is approximated as two-thirds of the return on corporate capital, proprietors’ compensation per hour will also be two-thirds of employee's compensation per hour. The equation used to determine an appropriate adjustment ratio stems from the following identity:

25 CUY = ECM + KRC (CCC) + PCM + KRN (CCN)

where,

CUY = current $ income

ECM = employee's compensation

KRC = net corporate productive capital stock

CCC = corporate rental price

PCM = proprietors’ compensation

KRN = net noncorporate productive capital stock

CCN = noncorporate rental price

PHR = proprietors’ hours

REM = adjustment ratio

The initial estimate of noncorporate rental price used is corporate rental price. Proprietors’ compensation is initially estimated as proprietors’ hours (PHR) multiplied by employee's compensation per hour (ECM/EHR).

Thus:

26 PCM = PHR*(ECM/EHR)

The rental prices are divided into two parts. One part includes the rate of return (R). The other part includes depreciation less capital gains (D). The noncorporate rate of return is the part of the rental price that is adjusted downward or upward by an adjustment ratio (REM). This adjustment reflects the constraint (equation 25) that current dollar income must exactly equal payments to factors. The theory is that only this portion of the rental price lies within the proprietors’ control. Noncorporate depreciation and capital gains are assumed not to occur differently than in the corporate sector. Proprietors’ compensation is also adjusted downward or upward by this adjustment ratio. Note that this is equivalent to saying that:

27 PCM/PHR = REM((ECM/EHR)since PCM = REM(PHR(ECM/EHR)).

The equation used to derive the adjustment ratio is now as follows:

28 CUY = ECM + KRC (R+D) + REM (KRN(R)) + KRN (D) + REM(PHR(ECM/EHR)). 

Solving for the adjustment ratio:

29 REM = CUY – ECM – KRC (R+D) – KRN (D) (PHR (ECM/her)) + KRN (R)

In addition to this equation, we also assume an alternative hypothesis. All parts of noncorporate capital income (including depreciation less capital gains) are assumed to participate in the adjustment. This has the effect of increasing the base of the adjustment and smoothing it out. This alternative is reflected in equation (30):

30 REM = CUY - ECM - KRC (R+D) (PHR (ECM/EHR)) + KRN (R+D)

Measures of real compensation per hour reflect the adjustment of hourly compensation for changes in consumer prices. 

Real compensation per hour (RC) is computed as hourly compensation deflated by an index of consumer prices (CPI):

31 Real Compensation= Current $ compensation Hours of labor input Consumer price index

The price changes for recent quarters are based on the BLS Consumer Price Index for All Urban Consumers (CPI-U). For earlier periods consumer prices are based on the BLS Consumer Price Index research series (CPI-U-RS).

Unit labor costs (ULC) are computed as labor compensation (C) per unit of output, but are often represented as follows:

32 Unit labor costs= Compensation Hours of labor input Output Hours of labor input

This form highlights the relationships between unit labor costs, hourly compensation, and labor productivity.

Unit nonlabor payments (UNLP) include the nonlabor components of value added in a given sector—consumption of fixed capital, taxes on production and imports less subsidies, net interest and miscellaneous payments, business current transfer payments, rental income of persons, and the current surplus of government enterprises as well as profits—whereas unit nonlabor costs (UNLC) exclude profits. These measures are computed as:

33 Unit nonlabor payments= Current dollar output - Current dollar compensation Output

34 Unit nonlabor costs= Current $ output - Current $ compensation - Current $ profits Output

Labor’s share (LS) in current dollar output in a given sector is the ratio of labor compensation paid in that sector to current dollar output:

35 Labor share= Current dollar compensation Current dollar output

Analogously, the non-labor or capital share is defined as follows:

36 Nonlabor share = Current $ output - Compensation Current $ output

37 =1-Labor Share

Presentation of data

Most of the measures are presented quarterly and annually in index form. Indexes are computed from basic data or analytic ratios by dividing the series by its own base year annual value and multiplying by 100. In addition, quarterly percent changes at a compound annual rate and percent changes from the same quarter in the previous year are computed:

38 Q t = 100 V t V t - 1 4 - 100

Y t = 100 V t V t - 4 - 100

where,

T          is a time subscript denoting the quarter,

V          is a series,

Q t         is the quarterly percentage change in series V from quarter t-1 to quarter t, measured at a compound annual rate, and

Yt         is the percentage change in series V from quarter t-4 (the same quarter 1 year before) to quarter t.

Indexes are published to three decimal points and percent changes are published to one decimal point.^⁠14