An official website of the United States government
 United States Department of Labor
United States Department of Labor
This section defines key terms and concepts that are central to understanding how the Bureau of Labor Statistics (BLS) produces measures of productivity for different levels of the U.S. economy.
Productivity is a measure of economic performance that compares the amount of goods and services produced (output) with the amount of inputs used to produce those goods and services. BLS publishes two types of productivity measures: single-factor productivity and multifactor productivity. Labor productivity is the most widely used single-factor productivity measure.
Labor productivity is a measure of economic performance that compares the amount of goods and services produced (output) with the amount of labor hours worked to produce that output. Labor productivity is a ratio of output to hours worked. Therefore, a change in labor productivity reflects the change in output that is not explained by the change in hours worked. Labor productivity can increase over time for many reasons, including technological advances, improved worker skills, improved management practices, economies of scale in production, and increases in the amount of nonlabor inputs used (capital, energy, materials, and purchased services).
Measures of productivity are useful for tracking changes in efficiency and for determining the effects of technological change. Productivity analysis can also provide information to assess the impact of policy changes or external shocks on particular industries, and the resulting impact on economic growth of the larger economy. For productivity measurement, it is important that well-defined data on outputs and inputs exist, and that they are measured independently.
By the mid-1970s, there was a significant accumulation of research relevant to productivity measurement that had not yet been reflected in government measures. The idea of using production functions as a means of analyzing aggregate economic activity was pioneered by Paul Samuelson in 1947. In the following statement, the function, f, reflects the maximum amount of output (Y) that can be produced by various combinations of inputs of labor, L, and capital, K, given the technology available at time t:
![]()
where,
K = capital services
L = labor input
t = time
At = technology available at time t
Y = output
A production function is typically the constraint on a model of optimizing behavior by the firm; given a set of prices, the firm determines the proportions of inputs which minimize cost, constrained by technology. Production functions also led to the formulation of macroeconomic growth models. During the 1950s and 1960s, growth models became increasingly sophisticated and detailed. In 1958, Robert Solow used a production function to show the role of capital in labor productivity trends. By assuming a production function and perfect competition in input factor markets, we can calculate the rate at which the production function is shifting, the growth in multifactor productivity (MFP), by differentiating by time as follows:
![]()
where,
![]() and
and ![]() are the average shares of labor and capital, respectively, in total cost over time and
are the average shares of labor and capital, respectively, in total cost over time and
![]() = the change in the natural log of I over time t.
= the change in the natural log of I over time t.
We call the rate at which the function is shifting the growth rate of multifactor productivity. MFP is also referred to as total factor productivity or the “residual.” Solow showed that it follows that the rate of growth of labor productivity depends on the growth rate in the capital-labor ratio, weighted by capital’s share, and the growth rate of MFP:
![]()
Multifactor productivity measures describe the relationship between output in real terms and the combined inputs involved in its production. Changes in multifactor productivity do not reflect the specific contributions of capital services, labor input, and energy, materials, and purchased services. Rather, multifactor productivity is designed to measure the joint influences on economic growth of a number of factors that are not specifically accounted for on the input side, including technological change, efficiency improvements, returns to scale, reallocation of resources, improved skills of the workforce, better management techniques, and other on economic growth, allowing for the effects of capital and labor.
BLS estimates MFP growth using a growth accounting framework that assumes Hicks-neutral technical change and constant returns to scale.1
The multifactor productivity indexes for private business and private nonfarm business are derived by dividing a value-added output index by an index of combined inputs of capital services and labor input. Value-added labor productivity growth is equal to MFP growth plus the growth in the capital-to-labor ratio (capital intensity) weighted by capital’s share of cost plus the growth in labor composition weighted by labor’s share of cost.
The multifactor productivity indexes at the industry level are derived by dividing a sectoral output index by an index of the combined inputs of labor, capital services, energy (E), materials (M), and purchased business services (S).
Gross output is the total value of goods and services produced by an industry. Intermediate inputs are the foreign and domestically sourced goods and services used by an industry in the process of producing its gross output.
Value added is the difference between gross output and intermediate inputs and represents the cost of labor, capital, and taxes spent in producing gross output. The sum of value added across all industries in the economy is equal to gross domestic product for the economy.
Sectoral output is defined as gross output less intra-industry transactions. This measure defines output as deliveries to consumers outside the sector in an effort to avoid the problem of double-counting that occurs when one establishment provides materials used by other establishments in the same industry.2
Value-added output is used by BLS to measure productivity for aggregate sectors of the U.S. economy, including labor productivity in the business and nonfarm business sectors and multifactor productivity in the private business, and private nonfarm business sectors. At the National Income and Products Accounts (NIPA) industry level, labor and multifactor productivity are measured using a sectoral output concept.
The U.S. Bureau of Economic Analysis (BEA) calculates the measure of value-added output for the business sector by removing from GDP the gross product of general government, private households, and nonprofit institutions serving households. Output for these sectors is estimated primarily using data on labor compensation. The trends in such output measures will, by definition, move with measures of input data and will tend to imply little or no productivity growth. Therefore, BLS excludes these activities from aggregate value-added output in order to remove potential sources of bias specific to productivity measurement.
The measure of business-sector output used by BLS to measure productivity also excludes the value added of owner-occupied housing and the rental value of buildings and equipment owned and used by nonprofit institutions serving individuals. These components are excluded because no adequate corresponding labor input measures can be developed.
To measure multifactor productivity, BLS further restricts value-added output to the U.S. private business sector, which excludes the output of government enterprises. These enterprise data are removed because subsidies account for a substantial portion of capital income.
At the NIPA industry level, BLS uses a measure of sectoral output. The sectoral output measure defines output as deliveries to consumers outside the sector in an effort to avoid the problem of double-counting that occurs when one establishment provides materials used by other establishments in the same industry.3 As a result, the sectoral output definition is more closely aligned with gross output at the most detailed industry level as intrasectoral transactions fall to zero. However, at the aggregate economy level, sectoral output and value-added output measures converge as the intermediate inputs produced and consumed within the sector approach the value of all intermediate input purchases.
By using sectoral output for NIPA industry productivity measures, advances in productivity in individual industries contribute to aggregate economic growth. This is done directly through increased deliveries to final demand and indirectly through increased deliveries to other sectors in the form of intermediate inputs.4
BLS makes estimates of multifactor productivity for the total economy available. For these measures, the BEA estimate of GDP must be modified to expand the output of government sectors and nonprofit institutions, to include more complete estimates of capital service inputs such as land. BLS replaces capital consumption allowances with measures of nominal capital services for government sectors and nonprofit institutions and adds that into GDP.
Inputs are the resources used in the production of goods and services and include labor, capital services, energy, materials, and purchased services. For labor productivity, output is compared only to labor hours worked to produce that output. For multifactor productivity private business and private nonfarm business, we compare value added output to the inputs of capital and labor. For NIPA industry level multifactor productivity measures, we use the KLEMS (K-capital, L-labor, E-energy, M-materials, and S-purchased services) accounting framework that measures the sectoral output growth over and above the combined growth of these four inputs.
Hours worked is the total number of hours worked of all people in an industry or a sector. This includes paid employees, the self-employed (partners and proprietors), and unpaid family workers (those who work in a family business or farm without pay). In measuring productivity, it is appropriate to define “hours” as all hours spent working.5 This includes all hours spent on actual production of goods and services, as well as time that is incidental to production, such as paid time for traveling between job sites, coffee breaks, and machine downtime. Paid vacations and other forms of paid leave are best viewed as benefits rather than as time available for production and should not be included for productivity analysis in measured hours.
Labor input is an aggregation of hours worked of the different types of workers with different skills and experience. BLS computes this as a measure of hours worked adjusted by a labor composition index that weights the heterogeneous class of workers by their median wage.
Labor composition measures the effects of shifts in the age, education, and gender of the workforce on hours worked. Not every work hour contributes the same amount to output. The productiveness of an hour of labor can differ based on age, education, and gender. The labor composition index adjusts the total hours worked for the demographic composition of those hours, which requires identification of separate, heterogeneous groups whose working hours are likely to have varying rates of output.
The labor composition model is formed by generalizing production function to permit numerous types of labor input. For the private business sector, this is written as:
![]()
where,
Y = output
At = technology available at time t
ki = n types of capital assets
hi = m types of labor inputs
The above production function equation allows each type of labor input and each type of capital to have a specific effect on output. By taking the natural logarithm of both sides, differentiating with respect to time, and rearranging terms, the above equation can be expressed as the relationship between the multifactor productivity and the growth rate of output and the growth rates of the inputs:
![]()
where, the dot notation refers to the growth rate of that variable. The partial derivatives, ![]() represent output elasticities, or the percent change in output as a result of 1-percent increase in the corresponding input. However, these marginal products are not observable in practice. Per the assumption of constant returns to scale and perfect competition in product and input markets, each elasticity is equal to the share of total costs paid to that input. For labor input, this is calculated as the share of the total wage bill that is spent on each particular type of labor. An aggregate labor input equation can be derived:
represent output elasticities, or the percent change in output as a result of 1-percent increase in the corresponding input. However, these marginal products are not observable in practice. Per the assumption of constant returns to scale and perfect competition in product and input markets, each elasticity is equal to the share of total costs paid to that input. For labor input, this is calculated as the share of the total wage bill that is spent on each particular type of labor. An aggregate labor input equation can be derived:
![]()
where, ![]() is the instantaneous rate of change in composition-adjusted labor input, it can replaced by annual rates of change, calculated using the Törnqvist index method as the difference in the natural logarithm of successive observations, with weights equal to the average of the two period factor shares.
is the instantaneous rate of change in composition-adjusted labor input, it can replaced by annual rates of change, calculated using the Törnqvist index method as the difference in the natural logarithm of successive observations, with weights equal to the average of the two period factor shares.
BLS partitions the Current Population Survey (CPS) sample into gender × age category × education level worker groups, and computes the year-to-year growth in hours for independent categories of worker. The growth rate in hours worked by class of worker are Törnqvist aggregated into a measure of total labor-input growth, where the weight for each group is its median wage. The growth rate of hours is then subtracted from the Törnqvist aggregated measure of labor-hours growth to obtain the labor-composition growth. This growth is used to adjust the official measures of BLS hours worked to include the effect of the changing composition of the workers in the multifactor productivity estimates.6
Annual indexes of labor composition are computed for private nonfarm business, private business and NIPA-level industries.
Capital input, also known as capital services, is the flow of the services derived from physical assets (equipment, structures, inventories, and land) and intellectual property used to produce output.7 Financial capital is not included in these measures. Capital services are derived by first computing productive capital stocks, then computing the rental prices of capital, and finally computing the composition index.
The productive capital stock is measured as the sum of past investments net of deterioration. Past investments are assumed to decline in productive capacity according to an age-efficiency function, (a,Ω)—where a is the age of the asset and Ω is its maximum service life—that represents the proportion of the investment’s original productive capacity that remains at age a. Letting Kt denote the (net) productive capital stock of an asset in year t and It-a denote investment expenditures in year t-a (that is, t-a is the vintage of the asset), the productive capital stock for a group of identical assets that have a maximum service life of Ω is given by the following:8

BLS assumes a hyperbolic age-efficiency function, which we note as
![]()
(2)
![]()
where ![]() is a shape parameter and
is a shape parameter and ![]() is concave, linear, or convex depending on whether
is concave, linear, or convex depending on whether ![]() (β = 1 implies one-hoss shay, for example a light bulb that works all the time until it doesn’t work at all). BLS assumes β = 0.75 for structures and β = 0.5 for equipment.9
(β = 1 implies one-hoss shay, for example a light bulb that works all the time until it doesn’t work at all). BLS assumes β = 0.75 for structures and β = 0.5 for equipment.9
The age-efficiency function accounts for three avenues by which the productive capacity of a group of assets can decline. First, assets become physically less productive when used or require more downtime for maintenance or repairs. The second avenue is through obsolescence. The third is through failure. With all three of these avenues one would expect the age-efficiency function for an individual asset to be concave with respect to age.
The age-efficiency function in equation (2) assumes that all assets in the group have identical maximum service lives. However, assets within an asset group are heterogeneous and can be used differently, leading to different services lives. Thus, the investment data that BLS receive from BEA are for asset groups that contain similar assets, but likely have different maximum service lives.10 Within an asset category, maximum service lives can differ because the assets are heterogeneous or because the assets are used differently. Therefore, within an asset group, BLS assumes a distribution of maximum service lives for each type of asset and computes a cohort age-efficiency function that is a weighted average of the deterioration functions of the individual asset types.11
The cohort age-efficiency function for an asset category is denoted by
![]()
where the limits of the integral are the upper and lower bounds of the distribution of service lives, where ![]() and
and ![]() .
.
BLS assumes that ![]() is a modified truncated normal distribution with mean
is a modified truncated normal distribution with mean ![]() and
and ![]() . BLS truncates the normal distribution at ±2 standard deviations (
. BLS truncates the normal distribution at ±2 standard deviations (![]() ), shifting the density function downward so that it equals zero at the upper and lower bounds of the distribution, and then inflating the density function proportionately so that the final modified density,
), shifting the density function downward so that it equals zero at the upper and lower bounds of the distribution, and then inflating the density function proportionately so that the final modified density, ![]() , integrates to 1.
, integrates to 1.
The final capital stock for each industry and asset-category combination is estimated by substituting equation (3) for the age-efficiency function in equation (1):

Note that the upper limit of the summation differs from that in equation (1). In equation (1), maximum service life refers to homogeneous assets with a maximum service life of ![]() . But in equation (4), the maximum service life is the maximum of the longest lived asset in the asset category
. But in equation (4), the maximum service life is the maximum of the longest lived asset in the asset category ![]() . After the derivation of the capital stocks estimation of the rental price of capital begins.
. After the derivation of the capital stocks estimation of the rental price of capital begins.
The rental price of capital, or the user cost of capital, is the opportunity cost of holding and using it for a period of time. The industry considers investing in capital when the value of the marginal product of that investment is equal to the rental rate of capital.
For instance, when considering investing in a building, the investing industry knows it can earn returns over many years with a building. However, when it invests in a computer, the expectation of the industry is that the computer will be of only marginal usefulness in a few years. So industry must expect a dollar's worth of computer to yield services more intensely than a dollar's worth of building in order to justify the levels of investment in each.
Also, part of investment considerations are any taxes associated capital investment. The U.S. tax laws have varied from year to year, but they have generally favored investments in equipment by their tendency to make the effective cost of using equipment lower than the cost for structures. The laws accomplish this by allowing an investment tax credit for equipment and also by allowing depreciation deductions for equipment over very short periods of time. The rental price formula used by BLS includes a term which adds in property taxes assessed on the particular asset type, and a factor which adjusts the rental price for the effects on the returns to capital of the corporate income tax rate, depreciation deductions, and credits. This tax-adjusted rental price formula can be derived from the neoclassical assumption that the price of an investment good equals the discounted value of its future services plus the decline in the asset’s value. The assumption is applied to a price which is adjusted for any tax credit and to a stream of after-tax future income.
In its simplest form, the rental price for a period is set to the price of the asset multiplied by the sum of the rate of depreciation and the appropriate rate of return:
![]()
where,
ct is the rental price for period t,
pt is the price of the asset,
rt is the rate of return, and
dt is the rate of depreciation.
In addition to the price of asset, its rate of return and rate of depreciation BLS also accounts for inflation in the price of new assets and the effects of taxes. The BLS equation for the rental price is given by:
![]()
where,
ut is the corporate income tax rate,
zt is the present value of $1 of the depreciation deduction,
et is the effective rate of the investment tax credit (zero since 1979),
rt is the nominal industry-specific internal rate of return on capital,
dt is the average rate of economic depreciation of asset j in industry i,
![]() is the asset-specific (for asset category j) deflator for new capital goods,
is the asset-specific (for asset category j) deflator for new capital goods,
![]() is the revaluation of assets due to inflation in new goods prices (asset category j), and
is the revaluation of assets due to inflation in new goods prices (asset category j), and
xt is the rate of indirect taxes.
Rental prices are computed separately for each asset category and industry combination. Data are available, or easily calculated, for all of the variables in equation (6) except the internal rate of return, r.12
Wealth stock measures the financial value of the capital stock, rather than its productive capacity. Analogously, depreciation measures the decline in the financial value of the capital stock rather than the decline in its productive capacity. BLS calculates the wealth stock in order to estimate depreciation. Wealth and productive stock are linked through the age-efficiency function, with the main difference between the productive capital stock and the wealth stock is that the productive stock is a point-in-time measure (the current productive capacity of past investments), whereas the wealth stock is a forward looking measure (the discounted value of the remaining productive capacity of the productive capital stock).
The wealth stock is equal to the age-adjusted price of the asset multiplied by real investment summed over all asset cohorts that have positive productive capacity at time t:
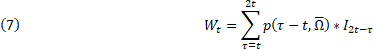
where ![]() is the price of an a-year-old asset (group) that has an average maximum service life of
is the price of an a-year-old asset (group) that has an average maximum service life of ![]() . The age-price function is derived from the cohort age-efficiency function and is equal to the discounted value of the remaining productive capacity of the asset divided by the discounted value of the productive capacity of the asset over its entire service life:
. The age-price function is derived from the cohort age-efficiency function and is equal to the discounted value of the remaining productive capacity of the asset divided by the discounted value of the productive capacity of the asset over its entire service life:
![]()
where, ![]() ) is the cohort age-efficiency function equation (3), and ρ is the real discount rate, which is assumed to be 4 percent per year. The age-price function declines over time from 1, when the asset is new, to 0 at the end of its service life. It declines more quickly than the age-efficiency function, because the financial value of an asset declines—because of decreased remaining service life—even if its productive capacity does not.
) is the cohort age-efficiency function equation (3), and ρ is the real discount rate, which is assumed to be 4 percent per year. The age-price function declines over time from 1, when the asset is new, to 0 at the end of its service life. It declines more quickly than the age-efficiency function, because the financial value of an asset declines—because of decreased remaining service life—even if its productive capacity does not.
The depreciation term is calculated as each year’s constant dollar investment minus the change in the wealth stock.
Internal rate of return is calculated by setting capital income equal to the product of the capital stock (from equation 4 and the rental price of capital defined in equation 6 above):
![]()
where Yit is nominal capital income in industry i and Kit is the productive capital stock in industry i. Substituting equation (6) for ct and arranging terms the internal rate of return is:
![]()
where Pi,t-1 is the industry level price deflator:
![]()
where Ji is the set of asset categories in industry i.13
An external rate of return is required when an implausibility arises with the capital income estimates. For instance, when the internal rate of return is negative due to large movements in the capital gains term. That, in turn, can drive the rental price negative and the capital costs negative, which would imply that someone was paying the industry to invest. Another reason BLS switched to using the rental price from the external rate of return instead of the internal rate of return is when abnormally large growth in the capital services are observed. A strangely behaving capital composition measure will also invoke the external rate of return, when the capital composition adjustment is abnormally large. Negative internal rates of return are the most common reason for using the external rate.
The proprietors’ income line released by BEA reflects the mixed income of both proprietors’ labor compensation as well as the capital income that proprietor will spend to build the business. Note that the capital income and components of value added are released by BEA and, for the labor compensation estimates, represent data for the employees only, not that of proprietors. BLS must divide the proprietors’ mixed income into the two primary inputs to production, capital and labor. Independent estimates of proprietors’ labor compensation and capital income are generated controlling to the total from the proprietors’ income estimate from BEA.
The initial estimate of proprietors’ labor compensation are made by assuming that the proprietors earn the same average hourly compensation as the employed workers. That compensation per hour estimate is multiplied by the number of proprietors to arrive at an independent measure of proprietors’ labor. In addition, BLS assumes that the proprietors’ capital rate of return is the same rate of return as their industry corporate counterparts allowing for an independent measure of capital income for the proprietors’ piece of capital income. After these two independent measures are computed, BLS scales the sum to the mixed income figure reported by BEA, evenly distributing any residual.
Similar to the labor contribution, the contribution of capital inputs to output growth can be decomposed into the contributions of changes in the capital stock and changes in the composition (“quality”) of the capital stock. The growth in capital input is calculated as a Törnqvist index of the growth of the productive capital stock for each asset, where the weights are the assets’ shares of capital costs. The effect of capital composition on output growth is simply the share weighted growth in capital input minus the growth in the share weighted capital stock. This decomposition is exactly analogous to the decomposition of labor input into changes in hours worked and changes in the composition of the workforce.14
BLS assumes that the growth in capital inputs is approximately proportional to the growth of the capital stock. Capital input growth is a Törnqvist aggregation of capital stock growth rates weighted by each asset and industry combination’s share of total capital cost (averaged over both years).15
Intermediate inputs are components of energy, nonenergy materials, and purchased services. For productivity measures calculated using a sectoral output measure at a more disaggregate level, it is important to include both primary inputs (capital and labor) and intermediate inputs. Price and quantity indexes of intermediate inputs are obtained from BEA's annual industry accounts. As with the sectoral output measures, materials inputs and services are adjusted to exclude transactions between establishments within the same sector. These adjustments equal the adjustments made on the output side as well.
Combined inputs is a measure of all the inputs that are used by an industry to produce output. At the more aggregate level where value added analysis is the most appropriate tool for evaluating output growth, combined inputs include labor and capital. Inputs are combined using chained superlative Törnqvist aggregation, applying weights that represent each component's two period average share of total costs. For each input, the weight is the input's share of total costs and is derived from BEA data on the components of nominal value added by industry. At both the sector and the industry levels, labor costs are measured as compensation to employees (wages, salaries, and supplements) plus a portion of proprietor’s income as mentioned previously. Most other components of nominal value added are assigned to capital. The exceptions are those taxes on production and imports which are not assigned to either capital or labor (notably sales and excise taxes).
Currently total cost is less than value added by an amount equal to these nonassigned taxes. Labor and capital shares in total cost are computed and then used in the aforementioned aggregation of capital and labor. The effect of computing the shares without taxes involved and applying that to the growth in the input and output statistics that have taxes embedded means that the nonassigned taxes are scaled across the inputs while maintaining their relative shares with each other.
For the more detailed sectors and industries where intermediate inputs have been shown to have an impact, sectoral output is used and the combined inputs include labor, capital, and the intermediate purchases of energy, materials, and purchased services.16
Labor compensation includes monetary and nonmonetary payments to or on behalf of individuals for labor services used to produce output. Workers may be employees, proprietors, and self-employed or unpaid family workers. Compensation of employees includes salaries, wages, bonuses, contributions to benefits plans, and other forms of payment. The compensation of employees in general government, nonprofit institutions, and private households are subtracted from compensation of employees in domestic industries to derive employee compensation for the business sector. For the nonfarm business sector, compensation further excludes farm employees. Proprietor’s income is computed independently and scaled to control totals as described above.
Capital costs is the cost to produce output of goods and services that is attributed to the use of capital. It includes corporate capital income plus imputed proprietor’s capital income. Corporate capital income includes the summation of corporate capital consumption allowances, corporate profits before tax without inventory valuation adjustment, corporate inventory valuation adjustment, corporate net interest and miscellaneous payments, corporate business transfer payments, and the part of taxes on production and imports associated with capital (property taxes and motor vehicle taxes). Proprietor’s income and capital costs are independently estimated and scaled to BEA control totals of proprietor’s mixed income described above.
Nonlabor payment is a measure of the excess of current-dollar output in an economic sector over corresponding labor compensation, and include nonlabor costs as well as corporate profits and the profit-type income of proprietors.
Unit labor costs measure the cost of labor input required to produce one unit of output and are derived by dividing hourly compensation of all persons in current dollars by the output per hour (labor productivity).
Unit nonlabor costs include the nonlabor components of value-added output in a given sector—consumption of fixed capital, taxes on production and imports less subsidies, net interest and miscellaneous payments, business current transfer payments, rental income of persons, and the current surplus of government enterprises—divided by the output index.
1 Robert M. Solow, “Technical change and the aggregate production function,” Review of Economics and Statistics 39, no. 3 (August 1957), pp. 312–20.
2 Further information on this concept of output, see William Gullickson, "Measurement of productivity growth in U.S. manufacturing," Monthly Labor Review (July 1995), pp. 13–27, https://www.bls.gov/mfp/mprgul95.pdf.
3 Ibid.
4 Further information on the intermediate input concept of relating aggregate growth through industry growth, see Frank Gollop, “Accounting for intermediate input: the link between sectoral and aggregate measures of productivity growth,” Measurement and Interpretation of Productivity (The National Academies Press, 1979), pp. 318, https://www.nap.edu/read/9578/chapter/18.
5 Mary Jablonski, Kent Kunze, and Phillis Flohr Otto, “Hours at work: a new base for BLS productivity statistics,” Monthly Labor Review, (February 1990), https://www.bls.gov/opub/mlr/1990/02/art2full.pdf.
6 Cindy Zoghi, “Measuring labor composition. A comparison of alternate methodologies,” Labor in the New Economy (University of Chicago Press, 2010), http://www.nber.org/chapters/c10834.pdf.
7 For more information on capital inputs, see Lucy P. Eldridge, Chris Sparks, and Jay Stewart, “The U.S. Bureau of Labor Statistics productivity program,” The Oxford Handbook of Productivity Analysis (Oxford University Press, 2018), https://www.oxfordhandbooks.com/view/10.1093/oxfordhb/9780190226718.001.0001/oxfordhb-9780190226718-e-3 and Michael J. Harper, “Estimating capital inputs for productivity measurement: an overview of concepts and methods,” (paper presented at the Capital Stock Conference, March 10–14, 1997), http://www.oecd.org/sdd/na/2666894.pdf Passages are borrowed from and quoted throughout the capital input section as the authors of those sections were BLS employees at the time of the writings.
8 BEA and many academic studies assume geometric deterioration, where the rate of deterioration is constant over time. This simplifies calculations, because this deterioration rate can be applied to the entire stock of capital, so there is no need to keep track of assets’ vintages. However, Michael Harper concluded that this assumption was unrealistic in many cases because assets’ productivity tend to decline slowly at first and more rapidly as they approach their maximum lifespans.
For more information on deterioration, see Harper, Michael J. "The Measurement of Productive Capital Stock, Capital Wealth and Capital Services," BLS Working Paper No. 128, 1982. Analysis of the computation of capital depreciation for productivity measurement, and Michael Harper, “Estimating Capital Inputs for Productivity Measurement: An Overview of U.S. Concepts and Methods,” International Statistical Review, no. 3, 1999, pp. 327–37.
9 These values were chosen because they are close to values estimated by Charles Hulten and Frank Wykoff using actual data.
1010 BEA provides the BLS with information on service lives and depreciation rates. BLS does not use BEA service lives. Instead, BLS estimates service lives so that, when used in conjunction with the hyperbolic age-efficiency function, they are consistent with BEA depreciation rates.
11 Because average maximum service lives are estimates and there are no data about individual asset types with categories, the distribution can also be viewed as accounting for the uncertainty, as well as heterogeneity.
12 Depreciation is calculated as the change in wealth stock minus the current year’s investment. The depreciation rate is equal to depreciation divided by the wealth stock, although in practice BLS uses the productive capital stock because it is less volatile than the wealth stock. The present value of $1 of tax depreciation allowance is calculated using equations from Robert Hall and Dale Jorgenson, and the deflator is calculated from the real and nominal investment data BLS gets from BEA. Use of the internal rate of return is necessary because of the assumption of perfect competition, which requires that profits be zero in equilibrium.
For more information on depreciation, see Robert E. Hall and Dale Jorgenson, “Tax policy and investment behavior,” American Economic Review, (June 1967), http://web.stanford.edu/~rehall/Tax-Policy-AER-June-1967.pdf
13 Note that equation (6) is defined for an industry × asset combination, whereas the rental price in equation (9) is defined for an industry only. Since capital income is available only at the industry level, equation (6) is modified using equation (11) so that the rental price used in the derivation of equation (10) is defined at the industry level.
14 Capital input can also be decomposed by type of asset to show the portion of capital input attributable to each type of asset.
15 This description glosses over many details. The Törnqvist aggregation is done in two steps, with the BEA asset categories being aggregated into seven asset groups for each industry (equipment, structures, land, rental residential capital, inventories, intellectual property products, and “all assets”). These asset group × industry combinations are then combined using the Törnqvist formula to arrive at the required intermediate and final aggregates.
16 Frank Gollop, “Accounting for intermediate input: the link between sectoral and aggregate measures of productivity growth,” Measurement and Interpretation of Productivity (National Academy of Productivity 1979), pp. 332, https://www.nap.edu/read/9578/chapter/18#332.