An official website of the United States government
 United States Department of Labor
United States Department of Labor

Crossref 0
The Geometric Young Formula for Elementary Aggregate Producer Price Indexes, Journal of Official Statistics, 2022.
Introducing Producer Price Index research series based on a geometric-mean formula, Monthly Labor Review, 2024.
This article examines the substitution effect in Producer Price Index (PPI) data for final- and intermediate-demand goods. The analysis demonstrates that PPIs calculated with Fisher and Tornqvist formulas, which allow for substitution, are generally lower than PPIs calculated with a Laspeyres formula. This result implies that the effect of substitution toward relatively less expensive goods dominates the effect of substitution toward relatively more expensive goods.
The Producer Price Index (PPI) measures the average change in prices received by domestic producers for their marketed output. The principal PPIs used for analyzing high-level inflation, and the focus of this article, are the Final Demand–Intermediate Demand (FD–ID) price indexes. Final-demand PPIs measure price change for outputs sold for personal consumption, as capital investment, to government, and as exports. Intermediate-demand PPIs measure price change for outputs sold to businesses as inputs to production, excluding capital investment.1
PPIs are calculated with a modified Laspeyres formula. To accurately reflect the relative importance of items included in an overall index category, the PPI program calculates its price indexes by using weights. In the modified Laspeyres formula, these weights are fixed quantities (over a 5-year period), but the formula allows prices to vary monthly. Having fixed quantities as weights restricts product substitution in response to relative price change, causing PPI data not to reflect the substitution effect, which is the effect on price measurement of shifts in production and purchase patterns in response to relative price changes.
Using fixed-base Laspeyres, Paasche, Fisher, and Tornqvist formulas, this article examines the substitution effect in PPI data by reestimating, on an annual basis, selected FD–ID PPIs from 2002 through 2016. To measure the substitution effect, the analysis compares the indexes calculated with Fisher and Tornqvist formulas (both of which allow for substitution) with corresponding indexes calculated with a Laspeyres formula. Importantly, there are no clear expectations about the direction of the substitution effect. In theory, purchasers tend to shift toward relatively less expensive products in an effort to reduce costs or increase utility, whereas producers tend to shift toward relatively higher priced products in order to maximize profits. The substitutions observed in the market are the net result of producer and purchaser responses that potentially work in the opposite directions.
Several studies have analyzed the substitution effect by using consumer price data. These studies typically find that the dominant substitution effect is one of consumers shifting toward relatively cheaper products. For example, Steven D. Braithwait measures the substitution effect by comparing a Laspeyres index with a cost-of-living index from 1958 through 1973.2 Using annual price and quantity data, the author finds that, compared with the cost-of-living index, the Laspeyres index overstated inflation by approximately 1.5 percentage points (about 0.1 percentage points per year) over the entire 15-year period. By examining detailed product categories within personal consumption, Braithwait also finds that the substitution effect varied by class of product. For example, from 1958 through 1973, the substitution effect for household durables was approximately 3.9 percentage points, whereas that for housing and utilities was only 0.1 percentage points. Using personal consumption data for 101 commodities from 1959 through 1985, Marilyn E. Manser and Richard J. McDonald examine the substitution effect by comparing fixed-base Laspeyres and Paasche indexes with Tornqvist and Fisher indexes.3 The authors find that, compared with the Tornqvist index, the Laspeyres index overstated inflation by approximately 0.19 percentage points per year over the entire period. Using weights based on annual consumer expenditure data for 207 product categories, Ana M. Aizcorbe and Patrick C. Jackman measure the substitution effect in the Consumer Price Index (CPI) by calculating fixed-base and chained Laspeyres indexes from 1982 through 1991 and comparing them with fixed-base and chained Tornqvist and Fisher indexes.4 The authors estimate that the Laspeyres index exceeded the Tornqvist index by 2.6 index points over the period, which is approximately 0.2 percentage points per year. Finally, a 1996 report by the U.S. Advisory Commission to Study the Consumer Price Index (commonly known as the Boskin Commission report) found that the CPI overstated inflation by 0.15 percentage points per year because of upper level (cross-commodity) substitution and by 0.25 percentage points per year because of lower level (within-commodity) substitution.5
While commonly examined with consumer price data, the substitution effect is rarely studied with producer price data. In a 1998 working paper cited by Keith Waehrer, Jack Galvin and Kenneth Stewart use both Laspeyres and Paasche formulas to calculate high-level PPI commodity indexes from 1987 to 1992.6 The authors find that, for 13 of the 15 commodity groups they examined, the Laspeyres index increased more than the Paasche index, indicating substitution into relatively cheaper products. Like Galvin and Stewart’s paper, the present article examines the substitution effect by using producer price data. This examination is important because, unlike studies using consumer price data, it can reveal substitution patterns at an earlier point in the supply chain. The article demonstrates that the experimental FD–ID indexes calculated with formulas allowing for substitution are generally lower than the indexes calculated with a Laspeyres formula. This result implies that the effect of substitution toward relatively less expensive products dominates the effect of substitution toward relatively more expensive products.
As noted earlier, the PPI program’s FD–ID indexes are high-level indexes that measure price change for outputs sold for personal consumption, as capital investment, to government, and as exports (final demand) and outputs sold to businesses as inputs to production (intermediate demand). These indexes are not constructed directly from price data but are instead calculated by combining detailed PPI commodity indexes. PPI commodity indexes are lower level price indexes that measure price change for specific products (e.g., beef and veal, processed poultry, unleaded regular gasoline, hardwood lumber, or automobiles). At their lowest level, commodity indexes are calculated directly from detailed price data with the use of a modified Laspeyres formula, in which weights are derived from data collected from survey respondents. To construct the FD–ID indexes, PPI aggregates commodity indexes into higher level price indexes by using a modified Laspeyres formula. The calculation uses aggregation weights based on value-of-shipments data from the quinquennial Economic Census and use-of-commodities-by-industry data from the U.S. Bureau of Economic Analysis.7 Every 5 years, PPI updates the weights used to calculate the FD–ID indexes.
In analyzing the substitution effect in PPI data, this article uses fixed-base Laspeyres, Paasche, Fisher, and Tornqvist formulas to estimate, on an annual basis, experimental FD–ID goods indexes for 2002–16. The article focuses on goods because an annual weight source is more readily available for detailed goods products included in the PPI than for services and construction products. (A description of how weights were constructed is provided toward the end of this section.) The experimental FD–ID indexes are estimated from the annual average values of 662 component PPI commodity indexes. The component commodity indexes are those calculated by the PPI program with the use of its standard modified Laspeyres formula. The FD–ID index calculation formulas can be written as follows:
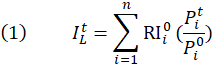
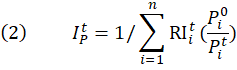
![]()
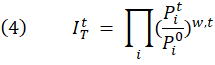
In these formulas, the subscript ![]() denotes each of the
denotes each of the ![]() component commodities included in the index calculation,
component commodities included in the index calculation, ![]() is the Laspeyres index at time
is the Laspeyres index at time ![]() ,
, ![]() is the Paasche index at time
is the Paasche index at time ![]() ,
, ![]() is the Fisher index at time
is the Fisher index at time ![]() ,
, ![]() is the Tornqvist index at time
is the Tornqvist index at time ![]() ,
, ![]() is the relative importance of component index
is the relative importance of component index ![]() in the base period,
in the base period, ![]() is the relative importance of component index
is the relative importance of component index ![]() in period
in period ![]() ,
, ![]() is the component index value in period
is the component index value in period ![]() ,
, ![]() is the component index value in the base period, and
is the component index value in the base period, and ![]() . The relative importance for component
. The relative importance for component ![]() in period
in period ![]() is calculated as
is calculated as
![]()
where ![]() is the value of shipments for commodity
is the value of shipments for commodity ![]() in period
in period ![]() .
.
Statistical agencies, including the U.S. Bureau of Labor Statistics, often use Laspeyres indexes to measure price change because doing so requires only base-period value-of-shipments data for weighting. Current-period value-of-shipments data are typically not available in a timely manner.8 As noted earlier, however, using base-period weight data restricts substitution in response to relative price change. In contrast, Fisher and Tornqvist indexes use a combination of current-period and base-period value-of-shipments data for weighting, relaxing the substitution restriction imposed by Laspeyres indexes. The Fisher and Tornqvist indexes are superlative indexes generally considered better approximations of the theoretical indexes on which PPIs are based.9 Assuming that a superlative index (such as a Fisher or a Tornqvist index) is a better measure of producer price change than a nonsuperlative index, one can measure the substitution effect by comparing the superlative index with the nonsuperlative Laspeyres index.
Calculating the indexes in equations (1) through (4) first requires constructing annual weights for the component indexes. Value-of-shipments data from the U.S. Census Bureau Annual Survey of Manufactures are used to construct weights for the manufacturing sector commodities.10 Weights for agricultural products are constructed with data from the annual Census of Agriculture of the U.S. Department of Agriculture, and finfish and shellfish weights are constructed with data from the annual Fisheries of the United States report of the National Oceanic and Atmospheric Administration.11 An annual data source for mining and utilities weights is not available. To overcome this problem, the analysis uses U.S. Census Bureau data when available (every 5 years), and for missing years, it uses estimates obtained by multiplying these data by the appropriate annual changes in the Federal Reserve’s indexes for industrial production (to account for commodity quantity changes) and then by the annual change in PPIs (to account for commodity price changes).12 The census, industrial production, and PPI data are all available in a form based on the North American Industry Classification System (NAICS). Missing census values are therefore estimated by using the closest matching NAICS-based indexes for industrial production and producer prices. After constructing the weights, the analysis estimates the
The design of this study only allows estimation of the substitution effect based on substitution across PPI commodity categories and not within commodity categories. In the calculation of the experimental superlative
To examine the substitution effect, the analysis looks at both long- and short-term index movements.
Figure 1 presents the PPI for final-demand goods from 2002 through 2016. The index is calculated with the use of Laspeyres, Paasche, Fisher, and Tornqvist formulas. As seen in the figure, the Laspeyres index is higher than the Paasche index over the entire 14-year period, and the Fisher and Tornqvist indexes are very close to each other, falling between the Laspeyres and Paasche indexes. The gap between the Laspeyres and Paasche indexes is generally growing throughout the sample period, but it narrows between 2009 and 2011. Over the entire period, the Laspeyres and Paasche indexes rise by 37.1 percent and 31.7 percent, respectively. Both the Fisher and Tornqvist indexes rise by about 34 percent. The substitution effect, calculated by subtracting the Tornqvist index from the Laspeyres index, is positive and approximately 3.4 percentage points over the period, indicating that the Laspeyres index overstates inflation by 0.18 percentage points per year. These findings for final-demand goods are very similar to those reported in Manser and McDonald’s and Aizcorbe and Jackman’s studies, which, using consumer data, estimate the annual substitution effect to be 0.19 and 0.2 percentage points, respectively.13 Although the PPI for final demand measures price change based on prices received by producers, it reflects price change for commodities sold to specific types of buyers (consumers, government, capital investors, and foreign purchasers of U.S. exports), with sales to consumers being the largest component. In this way, the PPI for final demand is very similar to an index measuring price change from the purchaser’s perspective. The positive sign of the substitution effect implies that purchaser substitutions into relatively less expensive products dominate producer substitutions into relatively more expensive products. A possible cause of this pattern could be that, during the sample period, supply shifts are occurring more frequently than demand shifts.
| Year | Laspeyres | Paasche | Fisher | Tornqvist |
|---|---|---|---|---|
| 2002 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2003 | 104.07 | 103.13 | 103.60 | 103.52 |
| 2004 | 108.07 | 106.53 | 107.29 | 107.25 |
| 2005 | 113.48 | 111.55 | 112.51 | 112.66 |
| 2006 | 118.26 | 115.07 | 116.65 | 117.06 |
| 2007 | 121.92 | 117.80 | 119.84 | 120.61 |
| 2008 | 130.82 | 124.41 | 127.57 | 129.42 |
| 2009 | 124.81 | 120.65 | 122.71 | 124.05 |
| 2010 | 130.35 | 127.06 | 128.70 | 129.56 |
| 2011 | 139.48 | 137.73 | 138.60 | 139.04 |
| 2012 | 141.73 | 139.68 | 140.70 | 140.97 |
| 2013 | 143.06 | 140.38 | 141.71 | 142.02 |
| 2014 | 145.04 | 141.59 | 143.30 | 143.11 |
| 2015 | 138.89 | 134.21 | 136.53 | 135.98 |
| 2016 | 137.15 | 131.74 | 134.41 | 133.76 |
| Source: Author’s calculations based on Producer Price Index data from the U.S. Bureau of Labor Statistics. | ||||
The indexes for processed goods for intermediate demand and unprocessed goods for intermediate demand differ from the index for final demand in that they measure price change for goods sold to businesses as inputs to production (as opposed to goods sold to end users). The index for processed goods for intermediate demand measures price change for goods that have undergone some level of fabrication, whereas the index for unprocessed goods for intermediate demand measures price change for business purchases of unfabricated goods. Figures 2 and 3 present the intermediate-demand indexes, calculated with Laspeyres, Paasche, Fisher, and Tornqvist formulas, for the 2002–16 period.
| Year | Laspeyres | Paasche | Fisher | Tornqvist |
|---|---|---|---|---|
| 2002 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2003 | 105.13 | 104.62 | 104.87 | 104.86 |
| 2004 | 112.07 | 111.14 | 111.61 | 111.64 |
| 2005 | 121.01 | 119.86 | 120.43 | 120.65 |
| 2006 | 129.97 | 128.94 | 129.46 | 129.79 |
| 2007 | 133.66 | 133.34 | 133.50 | 134.02 |
| 2008 | 147.12 | 147.19 | 147.16 | 148.21 |
| 2009 | 135.12 | 135.66 | 135.39 | 135.73 |
| 2010 | 143.77 | 143.75 | 143.76 | 144.48 |
| 2011 | 156.57 | 155.58 | 156.07 | 157.66 |
| 2012 | 157.21 | 157.18 | 157.19 | 158.64 |
| 2013 | 157.33 | 156.65 | 156.99 | 158.49 |
| 2014 | 158.50 | 157.47 | 157.99 | 158.92 |
| 2015 | 147.77 | 145.03 | 146.40 | 146.52 |
| 2016 | 143.12 | 140.37 | 141.74 | 141.81 |
| Source: Author’s calculations based on Producer Price Index data from the U.S. Bureau of Labor Statistics. | ||||
| Year | Laspeyres | Paasche | Fisher | Tornqvist |
|---|---|---|---|---|
| 2002 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2003 | 125.92 | 125.17 | 125.54 | 125.59 |
| 2004 | 146.73 | 143.85 | 145.28 | 145.23 |
| 2005 | 168.31 | 163.17 | 165.72 | 166.05 |
| 2006 | 168.04 | 161.66 | 164.82 | 164.96 |
| 2007 | 185.99 | 184.48 | 185.23 | 185.63 |
| 2008 | 226.44 | 224.30 | 225.37 | 225.67 |
| 2009 | 156.28 | 157.63 | 156.95 | 157.29 |
| 2010 | 188.62 | 188.91 | 188.76 | 189.46 |
| 2011 | 220.45 | 220.22 | 220.33 | 221.28 |
| 2012 | 212.09 | 207.59 | 209.83 | 211.31 |
| 2013 | 218.79 | 219.34 | 219.07 | 220.85 |
| 2014 | 223.59 | 224.81 | 224.20 | 225.63 |
| 2015 | 168.86 | 160.36 | 164.56 | 164.96 |
| 2016 | 154.47 | 146.45 | 150.41 | 150.77 |
| Source: Author’s calculations based on Producer Price Index data from the U.S. Bureau of Labor Statistics. | ||||
For processed goods for intermediate demand, the Laspeyres index is higher than the Paasche index in all years except 2008 and 2009. Likewise, for unprocessed goods for intermediate demand, the Laspeyres index is higher than the Paasche index in all years except 2009, 2010, 2013, and 2014. Over the entire 14-year period, the Laspeyres and Tornqvist indexes for processed goods for intermediate demand rise by 143.1 percent and 141.8 percent, respectively. Therefore, compared with the Tornqvist index, the Laspeyres index overstates inflation by an average rate of 0.07 percentage points per year. For unprocessed goods for intermediate demand, the Laspeyres and Tornqvist indexes rise by 154.5 percent and 150.8 percent, respectively, over the period. Thus, compared with the Tornqvist index, the Laspeyres index overstates inflation by 3.7 percentage points, or 0.18 percentage points per year.
As evidenced by both the index for final demand and the indexes for intermediate demand, the substitution effect during the Great Recession and the subsequent recovery years differs from the substitution effect during the rest of the sample period. (The Great Recession began in December 2007 and ended in June 2009, but the economy continued to slowly return to a more normal state for several years after the recession, with the unemployment rate not falling below 5 percent until late 2015.) For final demand, the Tornqvist index is always lower than the Laspeyres index, but the two indexes are closer to each other during the Great Recession. The Tornqvist index for processed goods for intermediate demand actually exceeds the Laspeyres index from 2007 through 2014. In all years prior to the Great Recession, and after 2014, the Laspeyres index for processed goods for intermediate demand exceeds the Tornqvist index. A similar pattern is found for the index for unprocessed goods for intermediate demand. Owen J. Shoemaker also notes this pattern in comparing the chained CPI for All Urban Consumers (CPI-U) (calculated with a Tornqvist formula above the elementary level) with the regular CPI-U (calculated with a modified Laspeyres formula above the elementary level).14 He observes that, during 2008, the annual rate of change in the chained CPI-U was higher than the rate in the regular CPI-U. A potential area of future research would be to examine how the substitution effect changes during recessions.
For both final and intermediate demand, a long-term analysis of the substitution effect shows evidence of substitution toward relatively less expensive products. In general, the substitution effect seems stronger for final demand than for intermediate demand, which may imply that it is easier for final-demand purchasers to shift their purchases across commodities than for businesses to shift their inputs across commodities.
The previous section examined the substitution effect over the long term. PPI data, however, are often analyzed over the short term. For that reason, this section examines the substitution effect on an annual basis. Aizcorbe and Jackman note that, in short-term index analysis, measuring price change by using a ratio method (forming ratios of an index in two periods of interest) is valid for Laspeyres indexes but not for indexes obtained from many other formulas, such as the Fisher or Paasche formulas.15 Instead, a “true” method for measuring price change must be used, whereby the change is calculated with a formula in which the earlier comparison period is the base period. For example, the following formula would be used to calculate a percent change in a Paasche index between periods ![]() and
and ![]() :
:
![]() .
.
Table 1 presents annual percent changes in FD–ID goods indexes obtained from Laspeyres, Paasche, and Tornqvist formulas. For the Laspeyres indexes, the table includes percent changes calculated with the use of both the ratio and true methods. The true percent change is calculated with the Laspeyres formula (whereby the earlier comparison period is the base period), and the ratio percent change is calculated by forming ratios of the index in the two periods of interest. Table 2 presents estimates of the substitution effect, which is calculated by subtracting the annual percent change in the Tornqvist index from the annual percent change in the Laspeyres index. The substitution effect is calculated for both the true and ratio versions of the indexes. (For the full set of index changes measured by formulas, see appendix tables A-1, A-2, and A-3.)
| Year | Goods for final demand | Processed goods for intermediate demand | Unprocessed goods for intermediate demand | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Laspeyres | Tornqvist | Paasche | Laspeyres | Tornqvist | Paasche | Laspeyres | Tornqvist | Paasche | ||||
| True | Ratio | True | Ratio | True | Ratio | |||||||
| 2003 | 4.1 | 4.1 | 3.5 | 3.1 | 5.1 | 5.1 | 4.9 | 4.6 | 25.9 | 25.9 | 25.6 | 25.2 |
| 2004 | 3.6 | 3.8 | 3.5 | 3.4 | 6.4 | 6.6 | 6.4 | 6.3 | 16.3 | 16.5 | 15.7 | 15.2 |
| 2005 | 4.7 | 5.0 | 4.7 | 4.7 | 7.8 | 8.0 | 7.8 | 7.8 | 15.0 | 14.7 | 14.4 | 13.8 |
| 2006 | 4.3 | 4.2 | 4.0 | 3.7 | 7.7 | 7.4 | 7.4 | 7.2 | -0.5 | -0.2 | -0.9 | -1.2 |
| 2007 | 3.0 | 3.1 | 2.9 | 2.7 | 2.9 | 2.8 | 2.8 | 2.7 | 11.4 | 10.7 | 11.3 | 11.2 |
| 2008 | 6.9 | 7.3 | 6.8 | 6.7 | 10.1 | 10.1 | 10.1 | 10.1 | 22.1 | 21.8 | 21.7 | 21.4 |
| 2009 | -4.6 | -4.6 | -5.2 | -5.9 | -8.4 | -8.2 | -8.9 | -9.4 | -30.1 | -31.0 | -30.7 | -31.2 |
| 2010 | 4.7 | 4.4 | 4.6 | 4.4 | 6.8 | 6.4 | 6.6 | 6.4 | 21.9 | 20.7 | 21.0 | 20.3 |
| 2011 | 7.2 | 7.0 | 7.1 | 7.0 | 9.2 | 8.9 | 9.1 | 9.0 | 18.2 | 16.9 | 17.5 | 17.0 |
| 2012 | 1.5 | 1.6 | 1.5 | 1.5 | 0.3 | 0.4 | 0.4 | 0.4 | -3.6 | -3.8 | -4.5 | -5.4 |
| 2013 | 0.7 | 0.9 | 0.7 | 0.7 | 0.0 | 0.1 | 0.0 | 0.0 | 3.9 | 3.2 | 3.9 | 3.9 |
| 2014 | 1.2 | 1.4 | 1.2 | 1.1 | 0.5 | 0.7 | 0.5 | 0.5 | 1.9 | 2.2 | 1.4 | 0.9 |
| 2015 | -4.6 | -4.2 | -4.8 | -4.9 | -7.6 | -6.8 | -7.7 | -7.7 | -28.7 | -24.5 | -29.2 | -29.7 |
| 2016 | -1.5 | -1.3 | -1.6 | -1.7 | -3.2 | -3.1 | -3.3 | -3.4 | -8.8 | -8.5 | -8.9 | -9.2 |
| Source: Author’s calculations based on Producer Price Index data from the U.S. Bureau of Labor Statistics. | ||||||||||||
| Year | Goods for final demand | Processed goods for intermediate demand | Unprocessed goods for intermediate demand | |||
|---|---|---|---|---|---|---|
| True | Ratio | True | Ratio | True | Ratio | |
| 2003 | 0.5 | 0.5 | 0.3 | 0.3 | 0.3 | 0.3 |
| 2004 | 0.1 | 0.3 | 0.1 | 0.3 | 0.6 | 0.8 |
| 2005 | 0.0 | 0.3 | 0.0 | 0.1 | 0.6 | 0.3 |
| 2006 | 0.3 | 0.2 | 0.2 | 0.0 | 0.4 | 0.7 |
| 2007 | 0.1 | 0.2 | 0.1 | 0.0 | 0.1 | -0.6 |
| 2008 | 0.1 | 0.5 | 0.0 | 0.0 | 0.3 | 0.0 |
| 2009 | 0.6 | 0.6 | 0.5 | 0.8 | 0.6 | -0.3 |
| 2010 | 0.2 | -0.1 | 0.2 | -0.2 | 0.9 | -0.3 |
| 2011 | 0.1 | -0.1 | 0.1 | -0.2 | 0.6 | -0.7 |
| 2012 | 0.0 | 0.1 | 0.0 | 0.0 | 0.8 | 0.7 |
| 2013 | 0.0 | 0.2 | 0.0 | 0.1 | 0.0 | -0.7 |
| 2014 | 0.0 | 0.2 | 0.0 | 0.2 | 0.5 | 0.8 |
| 2015 | 0.2 | 0.6 | 0.1 | 0.9 | 0.5 | 4.7 |
| 2016 | 0.1 | 0.3 | 0.1 | 0.2 | 0.2 | 0.4 |
| Source: Author’s calculations based on Producer Price Index data from the U.S. Bureau of Labor Statistics. | ||||||
The short-term analysis provides additional evidence that, in both final- and intermediate-demand PPI data, the Laspeyres index has an upward bias relative to the Tornqvist index. In the vast majority of cases, the annual rate of change in the Laspeyres indexes for final-demand goods, processed goods for intermediate demand, and unprocessed goods for intermediate demand is higher than the annual rate of change in the Tornqvist index. This is especially evident in comparing the values for the true Laspeyres indexes with those for the Tornqvist indexes. In no case is the annual percent change in the final- or intermediate-demand true Laspeyres indexes lower than the change in the Tornqvist indexes. In some cases, the percent changes are equal, but again, this primarily occurs during the Great Recession or the first few years of the recovery. On average, the annual percent changes in the true Laspeyres indexes for final-demand goods, processed goods for intermediate demand, and unprocessed goods for intermediate demand are 0.16, 0.12, and 0.46 percentage points higher than the corresponding changes in the Tornqvist indexes. Likewise, the annual percent changes in the ratio Laspeyres indexes for final-demand goods, processed goods for intermediate demand, and unprocessed goods for intermediate demand are 0.27, 0.18, and 0.44 percentage points higher than the corresponding changes in the Tornqvist indexes.
The short-term analysis of the substitution effect provides relatively clear evidence of substitution toward cheaper goods for both final and intermediate demand. Like the long-term analysis, the short-term analysis also finds that the substitution effect during the Great Recession is different from the substitution effect in normal economic times.
Using fixed-base Laspeyres, Paasche, Fisher, and Tornqvist formulas and annual weights derived from several sources, this article examined the substitution effect in PPI data for final- and intermediate-demand goods by calculating, on an annual basis, selected FD–ID indexes for 2002–16. To estimate the substitution effect, the analysis compared experimental superlative indexes with fixed-base Laspeyres indexes. The substitution effect was examined by looking at both long- and short-term index movements.
In the long-term analysis, the substitution effect for 2002–16 (calculated by subtracting the Tornqvist index from the Laspeyres index) was found to average 0.18 percentage points per year for final-demand goods, 0.07 percentage points per year for processed goods for intermediate demand, and 0.18 percentage points per year for unprocessed goods for intermediate demand. The short-term analysis also found that the substitution effect for purchases of final-demand goods is toward relatively cheaper products. In an annual comparison of true Laspeyres indexes with Tornqvist indexes, the rate of change in the Laspeyres indexes for final-demand goods, processed goods for intermediate demand, and unprocessed goods for intermediate demand was found to be upwardly biased by, respectively, 0.16, 0.12, and 0.46 percentage points per year, on average.
Both the long- and short-term analyses indicate that the substitution effect during the Great Recession and immediate postrecessionary years differed from the substitution effect observed at other times in the sample period. Again, a possible area of future research would be to analyze how the substitution effect differs across recessionary periods, periods of high economic growth, and normal economic times. A second possible area of further research would be to extend the present analysis by including data for the services and construction sectors of the economy. As noted earlier, this article focused on goods indexes primarily because annual weight data for detailed PPI products are readily available.
Jonathan C. Weinhagen, "Measuring the substitution effect in Producer Price Index goods data: 2002–16," Monthly Labor Review, U.S. Bureau of Labor Statistics, July 2020, https://doi.org/10.21916/mlr.2020.16
1 For additional information on the calculation of PPIs and FD–ID indexes, see chapter 14, “Producer prices,” Handbook of Methods (U.S. Bureau of Labor Statistics, 2014), https://www.bls.gov/opub/hom/pdf/ppi-20111028.pdf.
2 Steven D. Braithwait, “The substitution bias of the Laspeyres price index: an analysis using estimated cost-of-living indexes,” American Economic Review, vol. 70, no. 1, March 1980, pp. 64–77.
3 Marilyn E. Manser and Richard J. McDonald, “An analysis of substitution bias in measuring inflation, 1959–85,” Econometrica, vol. 56, no. 4, 1988, pp. 909–930.
4 Ana M. Aizcorbe A. and Patrick C. Jackman, “The commodity substitution effect in CPI data, 1982–91,” Monthly Labor Review, December 1993, pp. 25–33, https://www.bls.gov/opub/mlr/1993/12/art3full.pdf.
5 Michael J. Boskin, Ellen R. Dulberger, Robert J. Gordon, Zvi Griliches, and Dale Jorgenson, Toward a more accurate measure of the cost of living, final report to the Senate Finance Committee from the Advisory Commission to Study the Consumer Price Index (Washington, DC: Senate Finance Committee, December 4, 1996). In response to the Boskin report, CPI implemented a geometric mean formula at the elementary level to address lower level substitution. In 2002, it began publishing the chained CPI for All Urban Consumers (CPI-U) in order to address upper level substitution. See Kenneth V. Dalton, John S. Greenlees, and Kenneth J. Stewart, “Incorporating a geometric mean formula into the CPI,” Monthly Labor Review, October 1998, pp. 3–7, https://www.bls.gov/mlr/1998/10/art1full.pdf; and Robert Cage, John S. Greenlees, and Patrick Jackman, “Introducing the chained Consumer Price Indices,” in Thierry Lacroix, ed., International Working Group on Price Indices (Ottawa Group): Proceedings of the Seventh Meeting (Paris: INSEE, 2003), pp. 213–246.
6 Keith Waehrer, “A comparison of the substitution effects for input and output price indexes,” Working Paper 327 (U.S. Bureau of Labor Statistics, April 2000), https://www.bls.gov/osmr/research-papers/2000/pdf/ec000020.pdf; and Jack Galvin and Kenneth Stewart, “Alternative measures of price change for the U.S. Producer Price Index,” Mimeo (U.S. Bureau of Labor Statistics, 1998).
7 The U.S. Bureau of Economic Analysis use-of-commodities-by-industry data can be found at https://www.bea.gov/industry/benchmark-input-output-data. Economic Census data can be found at https://www.census.gov/programs-surveys/economic-census.html.
8 The U.S. Bureau of Economic Analysis personal consumption expenditures price index and the chained CPI, both of which use superlative formulas that rely on current-value weights, are subject to revision because final current-period weight information is not available at the time of their initial publication.
9 The International Monetary Fund Producer Price Index manual shows that, under certain conditions, Fisher and Tornqvist indexes can approximate theoretical producer output price indexes. See Producer Price Index manual: theory and practice (International Monetary Fund, 2004), pp. 442–444.
10 For more information on the U.S. Census Bureau Annual Survey of Manufactures, see https://www.census.gov/programs-surveys/asm.html.
11 For more information on the U.S. Department of Agriculture Annual Census of Agriculture, see https://www.nass.usda.gov/AgCensus/index.php. The National Oceanic and Atmospheric Administration Fisheries of the United States reports can be found at https://www.noaa.gov/fisheries.
12 For Federal Reserve data on industrial production, see https://www.federalreserve.gov/releases/g17/Current/default.htm.
13 Manser and McDonald, “An analysis of substitution bias in measuring inflation”; and Aizcorbe and Jackman, “The commodity substitution effect in CPI data.”
14 Owen J. Shoemaker, “10 years of comparative results: chained C-CPI-U vs. regular CPI-U,” Joint Statistical Meetings 2013—Government Statistics Section (American Statistical Association, October 2013), https://www.bls.gov/osmr/research-papers/2013/pdf/st130020.pdf.
15 Aizcorbe and Jackman, “The commodity substitution effect in CPI data.”