An official website of the United States government
 United States Department of Labor
United States Department of Labor
The Consumer Price Index (CPI) is a measure of the average change over time in the prices paid by consumers for a representative basket of consumer goods and services. The CPI measures inflation as experienced by consumers in their day-to-day living expenses. The CPI is used to adjust income eligibility levels for government assistance, federal tax brackets, federally mandated cost of living increases, private sector wage and salary increases, and consumer and commercial rent escalations. Consequently, the CPI directly affects hundreds of millions of Americans.
In the Consumer Price Index (CPI), the urban areas of the United States are divided into 32 geographic areas, called index areas. The set of all goods and services purchased by consumers is divided into 211 categories called item strata: 209 Commodities and Services item strata, plus 2 housing item strata. The number of basic items used for the calculation of aggregate indexes is larger than this, at 243, because the entry level item (ELI) level is used for the calculation of basic cells for health insurance retained earnings (item code SEME) rather than the higher item stratum level. This results in 7,776 (32 x 243) item-area combinations.
Estimation of price change in the CPI is done in two stages. The first stage of CPI estimation is to calculate basic indexes for each of the 7,776 item-area combinations that compose the CPI. For example, the CPI-U series for electricity in the Philadelphia-Camden-Wilmington, PA-NJ-DE-MD CPI area is a basic index. The weights for this first stage come from the sampling frame for the item strata in the index area. Then, at the second stage, we calculate aggregate indexes by averaging across subsets of item-area combinations. For example, the all items index for Philadelphia is the aggregate of all 243 basic index series in that index area. Similarly, the U.S. city average index for electricity is the aggregate of the basic indexes for electricity in each of the 32 index areas. The U.S. city average all items CPI is the aggregate of all basic indexes. For the CPI-U and CPI-W, the weights for the second stage of aggregation are the biennial reference-period expenditures on the item strata in the index area, as calculated using expenditure data from the Consumer Expenditure Surveys.
For the majority of the 209 C&S strata, most information on price change comes from the commodities and services pricing survey. A few C&S strata including those for airline fares, intercity train fares, and used vehicles, use secondary sources of data on prices for their samples. For 24 strata with small weights, price movements are imputed from related strata.
Each month, the processing of the C&S survey data yields a set of price relatives, which are measures of short-term price change for all basic indexes. The CPI uses an index number formula to obtain an average price change for the items in each basic index’s sample. Most item strata use the geometric mean index formula, which is a weighted geometric mean of price ratios (the item’s current price divided by its price in the previous period) with weights equal to expenditures on the items in their sampling periods.
Calculations for a limited number of strata use a modified Laspeyres index number formula, which is a ratio of a weighted arithmetic mean of prices in the current period to the same average of the same items’ prices in the previous period, with estimated quantities of the items purchased in the sampling period serving as weights. The following strata use the Laspeyres formula:
Each month, the estimation system uses the following formulas to compute price relatives for each item-area combination (i,a).
The price relative (using a geometric mean formula) is given by
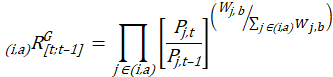
The price relative (using a Laspeyres formula) is given by
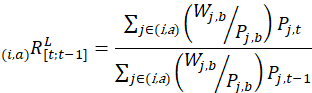
where,
![]() = the geometric price relative for the item-area combination (i,a) from the previous period t–1 to the current period t;
= the geometric price relative for the item-area combination (i,a) from the previous period t–1 to the current period t;
![]() = the Laspeyres price relative for the item-area combination (i,a) from the previous period t–1 to the current period t;
= the Laspeyres price relative for the item-area combination (i,a) from the previous period t–1 to the current period t;
![]() = the price of item j, which is a member of item stratum i, for which a price quote is being collected in area a, observed in period t;
= the price of item j, which is a member of item stratum i, for which a price quote is being collected in area a, observed in period t;
![]() = the price of the same item j in period t–1;
= the price of the same item j in period t–1;
![]() = an estimate of item j’ s price in the base period; and
= an estimate of item j’ s price in the base period; and
![]() = item j’s weight in the base period.
= item j’s weight in the base period.
The product and sums in the formulas presented above are taken over all price quotes which are usable for estimation in the item-area combination (i,a). It is important that the price of each quote be collected (or estimated) in both periods in order to measure price change.
For each individual quote, the weight, or each quote’s share of the average daily expenditure on the ELI in the primary sampling unit (PSU), is given by ![]() which is computed as
which is computed as
![]()
where
![]() = the proportion of CE expenditures for the ELI relative to the entire item category within the Census region;
= the proportion of CE expenditures for the ELI relative to the entire item category within the Census region;
![]() = estimate of the total daily expenditure for the item category in the PSU by people in the CPI-U population (called the basic weight);
= estimate of the total daily expenditure for the item category in the PSU by people in the CPI-U population (called the basic weight);
![]() = a duplication factor that accounts for any special subsampling of outlets and quotes;
= a duplication factor that accounts for any special subsampling of outlets and quotes;
![]() = a geographic factor used to account for differences in the index area’s coverage when the CPI is changing its area design;
= a geographic factor used to account for differences in the index area’s coverage when the CPI is changing its area design;
![]() = the number of quotes planned for collection in the item stratum PSU, which is also the sum of duplication factors for all sampled quotes in the item stratum PSU;
= the number of quotes planned for collection in the item stratum PSU, which is also the sum of duplication factors for all sampled quotes in the item stratum PSU;
![]() = the proportion of CE expenditures for the ELI relative to the item stratum within the region; and
= the proportion of CE expenditures for the ELI relative to the item stratum within the region; and
![]() = a nonresponse adjustment factor calculated as the quantity
= a nonresponse adjustment factor calculated as the quantity ![]() where y is the sum of duplication factors for uninitiated quotes and
where y is the sum of duplication factors for uninitiated quotes and ![]() is the number of quotes in the sample design in the ELI-PSU. This is the ratio of planned quotes to quotes with usable prices in both period t and period t–1 for the ELI-PSU.
is the number of quotes in the sample design in the ELI-PSU. This is the ratio of planned quotes to quotes with usable prices in both period t and period t–1 for the ELI-PSU.
In the modified Laspeyres formula used for C&S items, the quote weight is divided by an estimate of the item’s price in the sampling period to obtain an estimated quantity. An item’s base period occurs sometime before its outlet’s initiation, so one cannot observe its base-period price directly. Instead, the price is estimated from the item’s price at the time the sample was initiated and the best available estimates of price change for the period from the base period to the initiation period.
The price of an item, j, in the base period is given by
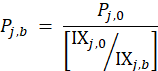
where
![]() = the price of item j at the time of initiation (period 0),
= the price of item j at the time of initiation (period 0),
![]() = the value of the price index most appropriate for item j at the time of initiation, and
= the value of the price index most appropriate for item j at the time of initiation, and
![]() = the value of the same price index in the base period.
= the value of the same price index in the base period.
One of the more difficult problems faced in compiling a price index is the accurate measurement and treatment of quality change due to changing product specifications and consumption patterns. The concept of the CPI requires a measurement through time of the cost of purchasing an unchanging, constant-quality set of goods and services. In reality, products disappear, products are replaced with new versions, and new products emerge.
When a data collector finds that he or she can no longer obtain a price for an item in the CPI sample (often because the outlet permanently stops selling it), the data collector uses the CPI item replacement procedure to find a new item. Each priced item stratum in the CPI contains one or more ELIs. CPI commodity analysts have developed checklists that define further subdivisions of each ELI. When seeking a replacement in a retail outlet, the data collector first uses the checklist for the ELI to find the item sold by the outlet that is the closest to the previously priced item. Then the data collector describes the replacement item on the checklist, capturing its important specifications. The CA assigned to the ELI reviews all replacements and selects one of three methods to adjust for quality change and to account for the change in item specifications.
The following example describes the most common type of quality adjustment problem. Assume that a data collector in period t tries to collect the price for item j in its assigned outlet and is not able to do so because the outlet no longer sells this item. (A price for item j was collected in period t–1.) The data collector then finds a replacement item and collects a price for it. This replacement item becomes the new version v+1 of item j. The commodity analyst decides how the CPI treats the replacement. The commodity analyst has the descriptions of the two versions of item j. In addition, he or she has the t–1 price, ![]() , for the earlier version v and the period t price,
, for the earlier version v and the period t price, ![]() , of the replacement version v+1. The following matrix displays the information available to the commodity analyst:
, of the replacement version v+1. The following matrix displays the information available to the commodity analyst:
|
Version |
Period t–1 price |
Period t price |
|
Old version v |
|
– |
|
Replacement version v+1 |
– |
|
To use the item in index calculation for period t, it is necessary to have an estimate of ![]() , which is the price of the earlier version v in the current period t. If there is no accepted way of estimating either
, which is the price of the earlier version v in the current period t. If there is no accepted way of estimating either ![]() or
or ![]() , the observation for item j is left out of the index calculation for period t, meaning that the observation is treated as a nonresponse handled by imputation.
, the observation for item j is left out of the index calculation for period t, meaning that the observation is treated as a nonresponse handled by imputation.
The three methods from which a commodity analyst can choose to handle the replacement follow.
If the original and replacement items are essentially the same, the CA deems them directly comparable, and the price comparison between the items is used in the index. In this case, it is assumed that no quality difference exists between the versions.
The most explicit method for dealing with a replacement item with a difference in quality is to estimate the value of the differences. The estimate of this value is called a quality adjustment amount, ![]() . In this case,
. In this case,
![]()
where
![]() = the period t price of the replacement version v+1, and
= the period t price of the replacement version v+1, and
![]() = the period t–1 price for the earlier version v.
= the period t–1 price for the earlier version v.
Sources of direct quality adjustment information include observable factors such as size or weight, manufacturers’ cost data, and hedonic regression models.
Imputation is a procedure for handling missing information. The CPI uses imputation for a number of cases, including respondent refusals, items which are out of season or unavailable for some other reason, and the inability to make a satisfactory estimate of the quality change. Replacement items that can be neither directly compared nor quality adjusted are called noncomparable. For noncomparable replacements, an estimate of constant-quality price change is made by imputation. There are two imputation methods used in the CPI: cell-relative imputation and class-mean imputation.
Cell-relative imputation
If there is no reason to believe that the price change for an item is different from the price change observed for the other items in its basic index, the cell-relative method is used to impute the change. This method is used for missing values, because no information is available about the observation in such cases. For noncomparable substitutions, this method is common for food and service items. The price change between the original item and the noncomparable replacement item is assumed to be the same as the average price change of all similar items in 1 month for the same geographic area, (i.e., the same as the average price change for the basic cell for that ELI and PSU). When there is a new version of the item that is not comparable to the previous version, a price of the new version is available. That price is not used in calculations for period t, but will be used in the subsequent period t+1 as the previous price.
Class-mean imputation
Some C&S item strata use a class-mean imputation for many noncomparable replacements, primarily in the item strata for vehicles, for other durables, and for apparel. The logic behind the class-mean procedure is that price change is closely associated with the annual or periodic introduction of new lines or models for many items. For example, at the introduction of new model-year vehicles, there are often price increases while, later in the model year, price decreases are common. The CPI uses the quality adjustment method as frequently as possible to handle item replacements that occur when product lines are updated. Class-mean imputation is employed in the remaining replacement situations. In those cases, the CPI estimates price change from the price changes of other observations that are going through an item replacement at the same time and that were either quality adjusted directly or judged to be directly comparable. For class-mean imputation, the CPI estimates ![]() , which is an estimate of the current period t price for the old version v, and uses this estimated current price in the calculation of the price relative for period t.
, which is an estimate of the current period t price for the old version v, and uses this estimated current price in the calculation of the price relative for period t.
The estimated current-period price is the previous period t–1 price of the old version multiplied by a specially constructed price relative for the class cR:
![]()
where ![]() is computed with either the geometric mean or Laspeyres formula over the subset of the observations in the ELI of which item j is a member. The subset is the class of interest, that is all the comparable and quality-adjusted replacement observations in the same ELI and PSU.
is computed with either the geometric mean or Laspeyres formula over the subset of the observations in the ELI of which item j is a member. The subset is the class of interest, that is all the comparable and quality-adjusted replacement observations in the same ELI and PSU.
All outlier price changes are reviewed by CAs. Outlier price changes, if accurate, are generally included in the calculation of price relatives. Extreme price changes are given upper and lower bounds, say 10 and 0.1.
The rent of primary residence (Rent) index and owners’ equivalent rent of primary residence (OER) index measure the change in the cost of shelter for renters and homeowners, respectively. Price change data for these two item strata come from the CPI housing survey. Each month, BLS data collectors gather information from renter units on the rent for the current month and on what services are provided. Rent and OER are each subject to their own unique estimation procedures.
The rent estimates used in the CPI are contract rents. They are the payment for all services provided by the landlord to the tenant in exchange for rent. For example, if the landlord provides electricity or other utilities, these would be part of the contract rent. The CPI item expenditure weights also include the full contract rent payment. Rents are calculated as the amounts the tenants pay their landlords, plus any rent reductions tenants receive for performing services on behalf of the landlord, plus any subsidy payment paid to the landlord. Reductions for any other reason are not considered part of the rent.
The OER approach to price change for owner-occupied housing is designed to measure the change in the rental value of the owner-occupied housing unit; the investment portion is excluded. In essence, OER measures the change in the amount a homeowner would pay in rent or earn from renting his or her home in a competitive market. It is a measure of the change in the price of the shelter service provided to the homeowner by the owner-occupied housing unit.
The housing sample is made up of renter-occupied units from the 2010 Decennial Census of Population and Housing in which higher rent levels (expenditures) have a higher probability of selection. The U.S. Census Bureau provided the numbers of renters and owners and the average rent of renter units in the block groups, and BLS estimated the average implicit rent of the owner units in the block groups. From these pieces of information, CPI calculated the total cost of rent in the block groups from the renter costs and the owner costs in the block groups.
The CPI breaks up each of the 75 CPI PSUs into small geographic areas, which are called segments. Segments are formed from one (in most cases) or more census block groups. The segments are sorted by PSU, state, county, average rent (or rent level) and tract. Blocks are portions of block groups, while tracts are portions of counties, and counties are portions of states. There can be more than one state in a PSU. The census data needed for sample selection are only available at the block group level.
Each calculation begins with a segment weight based on the probability of selecting the segment. A segment weight is the inverse of the probability of selection, where the probability of selection is the total housing cost for the segment multiplied by the number of segments to be selected in the PSU divided by the total housing cost for the PSU.
![]()
where
![]() = weight of segment s,
= weight of segment s,
![]() = the number of segments in the PSU,
= the number of segments in the PSU,
S = the segment, and
![]() = the total cost of rents in all block groups in segment S.
= the total cost of rents in all block groups in segment S.
![]()
where
![]() = the total cost of rents in all block groups in segment S,
= the total cost of rents in all block groups in segment S,
S = the segment, and
BG = the block group.
To derive the renter weight in the segment, the segment weight is multiplied by the number of renters in the segment and divided by the number of renters sampled in the segment:
![]()
where
![]() renter weight in segment s,
renter weight in segment s,
![]() segment weight,
segment weight,
![]() the number of renters in segment s, and
the number of renters in segment s, and
![]() the number of renters sampled in segment s.
the number of renters sampled in segment s.
Similarly, the owners’ equivalent rents weight is derived by multiplying the segment weight by the number of owners in the segment, and dividing by the number of renters sampled in the segment. Since the housing survey collects rents and not the implicit rents of owners, the ratio of average implicit rent to average rent in the segment is also included in the OER rent weight:
![]()
where
![]() owners’ equivalent rents weight in segment s,
owners’ equivalent rents weight in segment s,
![]() segment weight in segment s,
segment weight in segment s,
![]() number of owners in segment s,
number of owners in segment s,
![]() the number of renters sampled in segment s,
the number of renters sampled in segment s,
![]() average implicit rent in segment s, and
average implicit rent in segment s, and
![]() average rent in segment s.
average rent in segment s.
For the rent index, the current month’s index is derived by applying the sixth root of the 6-month rent change to the index for the previous month. For the OER index, the current month’s index is derived by applying the sixth root of the 6-month OER change to the index for the previous month.
The rent estimator uses the change in the economic rent, which is the contract rent adjusted for any changes in the quality of the housing unit, to estimate the change in the average rent. Due to the panel structure used in the housing sample, the 6-month change in rent is based on sampled, renter-occupied units that have usable 6-month rent changes. The sum of the current period economic rents for each usable unit within a segment, weighted by the renter weight for that segment, is divided by the sum of the weighted economic rents 6 months earlier t–6. This ratio is used to represent the 6-month change in rent for all renter-occupied units within a segment.
![]()
where
![]() = relative rent price change between months t and t–6 in segment s,
= relative rent price change between months t and t–6 in segment s,
![]() current period,
current period,
t–6 = period 6 months before the current period t,
![]() renter weight for segment s, and
renter weight for segment s, and
![]() economic rent of unit i in period t.
economic rent of unit i in period t.
The OER estimator uses the change in the pure rent which excludes the cost of any utilities included in the rent contract. In a parallel calculation to the rent estimator, the sum of the current pure rents for sampled, renter-occupied units within a segment, weighted by the owner weights, is divided by the sum of the weighted pure rents 6 months earlier.
This ratio is used to represent the 6-month change in the OER index for all owner-occupied housing units in the segment:
![]()
where
![]() relative OER price change between months t and t–6 in segment s,
relative OER price change between months t and t–6 in segment s,
t = current period,
![]() owners’ equivalent rent weight for segment s, and
owners’ equivalent rent weight for segment s, and
![]() pure rent for unit i in period t.
pure rent for unit i in period t.
The 6th root of the ![]() is calculated to provide 1-month price relatives for index estimation:
is calculated to provide 1-month price relatives for index estimation:
![]()
Vacant units that were previously occupied by renters are used in the calculation of relatives. The vacancy imputation process incorporates several assumptions about the unobserved rents of vacant units. It is presumed that rents tend to change at a different rate for units that become vacant (in the process of changing tenants) than for other units. The vacancy imputation model assumes that, after an initial lease period, expected rents change at a steady rate until the old tenant moves out of the unit. When there is a change in occupants or a unit becomes vacant, the rent is assumed to jump at some rate. In markets with generally rising rents, this jump rate is usually greater than the average rate of change for occupied units. BLS estimates the jump rate based on nonvacant sample units in the PSU which have had a change in tenant during the 6-month period between t–6 and t. Rent changes for nonvacant units without a tenant change are used to calculate the average continuous rate of change. These values are used to impute rents for vacant units in period t from their rent in period t–6.1
![]() if the unit was not vacant in t–6, or
if the unit was not vacant in t–6, or
![]() if the unit was vacant in t–6,
if the unit was vacant in t–6,
where
![]() imputed rent of vacant rental unit i in period t,
imputed rent of vacant rental unit i in period t,
J = the 6-month jump rate calculated for the PSU, and
C = the 1-month steady rate of change.
The imputation of vacant rents ensures that the unobserved rent change that occurs when a unit becomes vacant is reflected in the final index for rent. The 6-month rent-change estimates capture these changes once the units become occupied.
Housing units that were previously responding but not currently responding and not vacant are also imputed and used in the calculation of the 1-month and 6-month relatives. All units within a PSU are broken up into high, medium, and low rent categories based on their rent level in t–6. The rents of nonresponding, nonvacant units are imputed forward into t by using the average rent change of other housing units in their respective category.
The aging adjustment accounts for the small loss in quality as housing units age (or depreciate) between interviews. The aging adjustment factors are ![]() where d is the monthly rate of physical depreciation. BLS computes factors for each housing unit using a multinomial logistic regression that controls for the age of the unit and a number of structural characteristics.2
where d is the monthly rate of physical depreciation. BLS computes factors for each housing unit using a multinomial logistic regression that controls for the age of the unit and a number of structural characteristics.2
Seasonal items are those commodities and services that are available only at certain times of the year rather than year round. Down parkas, baseball tickets, and bathing suits are examples of seasonal items. Special procedures are employed when selecting and pricing items generally available only part of the year to ensure that they are appropriately represented in the sample and that price changes are correctly included in the calculation of the CPI. In particular, the procedures prevent replacing a seasonal item when it is out of season.
Although seasonal items can exist in any ELI, some ELIs include an especially large percentage of such items and, consequently, receive special treatment. These seasonal ELIs include most apparel items and admission to sporting events. The designation of an ELI as seasonal or nonseasonal is made at the regional level, using the four geographic census regions in the CPI design. Some items that exhibit a seasonal selling pattern in the Northeast region, for example, may be sold year round in the South. In practice, though, nearly all ELIs designated seasonal are seasonal in all four regions.
After the samples for these seasonal ELIs are selected following the normal sample selection procedures, the number of quotes is doubled. This doubling ensures that, despite the seasonal disappearance of a substantial number of quotes, a large enough number of in-season quotes remains to calculate the index.
The quotes in these ELIs are paired. For each original quote that is selected, a second quote in the same ELI and outlet is initiated and priced 6 months later. One quote of each pair is designated fall/winter, and one quote is designated spring/summer. The fall/winter and spring/summer designations are used because these are the distinctions that are most commonly used by the retail trade industry to categorize seasonal merchandise. These seasonal designations are used to help establish the specific items eligible for each quote so that year-round items and items from each season are initiated in their proper proportions.
Data collectors attempt to price every item in each period during which it is designated for collection, even during those months when the item may be out of its indicated season. If the item is available, the price is collected and used in the calculation of the CPI. A common practice in marketing seasonal items, particularly seasonal clothing, is to mark down prices to clear the merchandise from the stores as the end of each season approaches. During the period when a seasonal item is unavailable, its price is imputed following standard imputation procedures. When an item returns at the beginning of its season several months later, the price is directly compared with the item’s last price, as it has been imputed forward. This completes the circle in a sense: having followed the price of the item down to clearance price levels, BLS then follows the price back up to regular (or at least higher) prices the following season. (Keep in mind that, in this context, the “following” season means the same season the next year; that is, the following fall/winter season for the fall/winter sample, and the following spring/summer season for the spring/summer sample.)
When an item becomes permanently unavailable, the standard procedure is to replace it with the most similar item sold in the outlet. In the case of a year-round item that is not in a seasonal ELI, this process takes place as soon as the item is permanently unavailable. For items that are in seasonal ELIs and seasonal items in ELIs that are not designated seasonal, however, the period during which a replacement can take place is restricted to those months when a full selection of appropriate seasonal merchandise is available.
These special initiation, pricing, and substitution procedures are intended to ensure that an adequate sample of items is available every month, and that the correct balance of seasonal and year-round items is maintained. As a result, the estimates of price movement for the ELIs that include seasonal items correctly reflect price changes not just for items available year round but for the entire universe of items included in those ELIs.
There are many circumstances which can cause the price paid for goods and services by consumers to differ from the price posted. Where possible, BLS data collectors attempt to account for these circumstances, using a variety of procedures.
Sometimes, products are offered with free merchandise included with the purchase of the original item. Such “bonus” items may provide additional satisfaction to consumers, and BLS will, therefore, make adjustments to the purchase price to take into consideration the value of the bonus merchandise. The adjustment made depends on the type of merchandise offered and the perceived value of the bonus to the consumer. If the bonus merchandise consists of more of the same item, the adjustment is reflected in the price of the item. For example, if a manufacturer offer ounces of toothpaste free with the purchase of the regular 6-ounce tube, the item’s price is adjusted to reflect a decrease in the price per ounce. When the bonus is removed, the price per ounce returns to its previous level, and a price increase is recorded. In this instance, the value to the consumer is assumed to be one-third greater during the bonus period. If the bonus merchandise consists of an item that has some significant value to the consumer, and the item is different, an adjustment is made to account for the value of the free item when it is feasible to do so. Bonuses that are contingent on an additional unrelated purchase, such as a free can of soup when purchasing a whole chicken are ignored.
For a coupon to be used to reduce the reported price of an item, the coupon must be either attached to the item, attached to the product’s display shelf, dispensed by machines attached to the product’s display shelf, located at promotional displays, or distributed to all shoppers by product representatives standing in the immediate vicinity of the display shelf. All other coupons presented by customers as purchase reductions at the time of payment are ineligible.
A concession is a deduction of a specific amount from the proposed selling price for the item. The usual CPI practice is to subtract the average concession for the priced item over the past 30 days from the proposed selling price.
BLS collects information on container deposits for a variety of nonalcoholic and alcoholic beverages to reflect the influence of changes in deposit legislation on price change. Consumers who purchase throwaway containers are considered to be purchasing both the product itself and the convenience of throwing the container away. When a local jurisdiction enacts deposit legislation and no longer allows stores to sell throwaway containers, those consumers who were previously purchasing throwaway containers may experience a change in the price of this convenience. The price of the same-sized container of product plus its deposit establishes an upper bound for the price change, because the consumer could retain the former convenience by now purchasing returnables and simply throwing them away. In similar fashion, information about deposits and the status of legislation can be used to estimate price change when a container bill is repealed. Changes due to the enactment or repeal of container-deposit bills are shown in data for the month in which the legislation becomes effective.
For a subset of items, if the priced item that has been selected is not available for sale at the time of collection, prices from up to 7 days prior to the actual day of collection are eligible. The item must have been offered for sale during the previous 7 days and the most recently available price is reported. The list of eligible items generally consists of specific items that may not be available every day, such as a specific type of fresh fish.
A discount price is a reduced price that is available only to certain customers in a specific outlet. If the discount is available only during the period of price collection, such as a back-to-school discount, the discount is included only if 50 percent or more of sales for the affected item are discounted. If the discount is in effect for more than one collection period and the discount applies to 5 percent or more of the dollar sales of the item in the outlet, a probability selection is made to determine which price should be collected. For example, if the regular cash price accounts for 84 percent of sales, senior citizens’ discounts account for 10 percent and employee discounts account for 6 percent of sales, a one-time probability-based selection is made among the three options to determine which price to report.
When product manufacturers offer customers cash rebates at the time of purchase for items priced in the CPI, these rebates are reflected in the index as price reductions. When a rebate is offered for a priced new vehicle, it is the estimated average rebate over the past 30 days that is subtracted from the vehicle’s reported price. For vehicle leasing, it is the rebate in effect as of the day the collected price is obtained. For mail-in rebate offers, the price of the affected item is reported without subtracting the amount of the rebate. An attempt is made to determine the proportion of customers who take advantage of the rebate, and prior to its use in the index, the reported price is then adjusted accordingly.
Outlets that require a membership fee to be paid in order to be able to shop at the outlet are eligible for pricing in the CPI. If the actual price paid for products varies with the level of membership, a specific membership is selected and the reported prices reflect that membership level.
Many items in the CPI are sold both individually and in quantity. When consumers are able to purchase an amount greater than a single unit at a discounted price, the first multiple-unit price is reported for use in the CPI. For example, if the 12-ounce can of corn being priced can be purchased at 25 cents for a single can, three cans for 69 cents, or five cans for $1, the price used in the CPI will be the per ounce price of the three cans.
The CPI includes all applicable taxes paid by consumers for services and products purchased. Some prices for services and products used to calculate the CPI are collected with taxes included because this is the manner in which they are sold. Examples are tires and cigarettes. Other prices are collected excluding applicable taxes, with those taxes subsequently added in the Washington office. The tax rates for these items are determined from secondary sources based on the state, county, and local tax structure governing the sale of the service or product at the point of purchase.
If a priced outlet issues a card offering a card discount on selected products purchased by cardholders, such discounts are treated as temporary discounts and processed as follows. The discount is included only if signing up for the card is free and can be done by the consumer on the day of purchase.
If a selected outlet has different prices for priced items based on the day of the week when a purchase is made, a selection is made between special-day and regular-day purchases, based on revenue. If the “special day” is selected, the price collected is for the most recent special-day price.
When food items that are sold on a unit basis but lack a labeled weight are being priced, two items are weighed to permit calculation of an average weight for the item. This helps reduce the variability in size that occurs among individual, loose items and is not overly burdensome for the data collection process. For example, if the item being priced is red delicious apples, and the price is 50 cents each, the BLS field staff report the price of one apple and the combined weight of two apples taken from the produce bin. In computing the price per ounce, the combined weight is divided by 2, and the 50-cent price of the Red Delicious apple is divided by this average weight.
Sometimes, public utility commissions require that utilities such as telephone, natural (piped) gas, or electricity companies issue rebates to their customers for a number of different reasons. For example, a utility may be permitted to use a new rate schedule temporarily until a final determination is made. If the final rates set by the commission are lower than the temporary ones, the difference must be refunded for consumption during the period. The CPI does not always view such refunds as reflecting current period prices for utility services. If all customers, both new and existing, are subject to having the refund applied to their bill, then the refund is included in the total price calculation. However, if the refund is only applied to those customers who were originally subject to the overcharge (i.e., existing customers only) then the refund is excluded. This procedure reduces the month-to-month volatility of utility indexes and ensures that they reflect current prices and price trends more accurately. Also excluded are refunds that are paid directly to consumers in a separate check and are not part of the bill. The utility indexes do include current-period credits that are based on current consumption, such as purchased gas adjustments and fuel adjustments.
As stated earlier, the CPI is actually calculated in two stages. Earlier sections described the first stage of that calculation: how the CPI calculates the basic indexes, which show the average price change of the items in each of the 7,776 CPI item-area combinations. The next section describes the second stage of calculation: how the aggregate indexes are produced by averaging across the 7,776 CPI item-area combinations.
Aggregation of basic CPI data into published indexes requires three ingredients: basic indexes, basic expenditures to use as aggregation weights, and a price index aggregation formula that uses the expenditures to aggregate the sample of basic indexes into a published index.
The CPI-U, CPI-W, and initial, interim, and final versions of the Chained CPI-U are constructed by using the same combination of modified Laspeyres and geometric mean basic indexes. In other words, the prices for each series are combined in the same way to form the basic price indexes.
In the CPI-U and CPI-W, aggregating basic indexes into published indexes using a modified Laspeyres formula requires an aggregation weight for each item-area combination. The function of the aggregation weight is to assign each basic index a relative importance or contribution in the resulting aggregate index. The aggregation weight corresponds to consumer tastes and preferences and resulting expenditure choices among the 243 basic items in the 32 basic areas comprising the CPI sample for a specified period.
Aggregation weights (AW) are defined as:
![]()
where
![]() the estimated price of item i purchased in area a by population p in period
the estimated price of item i purchased in area a by population p in period ![]() , and
, and
![]() the estimated quantity of item i purchased in area a by population p in period
the estimated quantity of item i purchased in area a by population p in period ![]()
The period ![]() is the base period of the corresponding basic item-area index. For example, the “Sports equipment” (ITEM = RC02) for Seattle-Tacoma-Bellevue, WA (AREA = S49D) index series has a base period of
is the base period of the corresponding basic item-area index. For example, the “Sports equipment” (ITEM = RC02) for Seattle-Tacoma-Bellevue, WA (AREA = S49D) index series has a base period of ![]() = June 1985. CPI basic indexes have varying base periods, but most published indexes have an index base period of
= June 1985. CPI basic indexes have varying base periods, but most published indexes have an index base period of ![]() = 1982–84.
= 1982–84.
The period ![]() corresponds to the reference period of the expenditures used to derive the implicit quantity weights needed for Laspeyres aggregation. As of 2018, the CPI-U and CPI-W had an expenditure reference period of
corresponds to the reference period of the expenditures used to derive the implicit quantity weights needed for Laspeyres aggregation. As of 2018, the CPI-U and CPI-W had an expenditure reference period of ![]() = 2015–16. BLS uses a biennial rotation schedule for updating the expenditure reference period. Effective with the January 2016 index, the expenditure reference period changed from
= 2015–16. BLS uses a biennial rotation schedule for updating the expenditure reference period. Effective with the January 2016 index, the expenditure reference period changed from ![]() = 2011–12 to
= 2011–12 to ![]() = 2013–14; effective with the January 2018 index, it was updated again to 2015–16; and so forth. It is worth noting that a change in the expenditure reference period results in a change in the implicit quantity Q assigned to each basic index, but not the implicit price component p of the aggregation weight AW of each basic index.
= 2013–14; effective with the January 2018 index, it was updated again to 2015–16; and so forth. It is worth noting that a change in the expenditure reference period results in a change in the implicit quantity Q assigned to each basic index, but not the implicit price component p of the aggregation weight AW of each basic index.
Aggregation weights for the CPI-U and CPI-W are derived from estimates of household expenditures collected in the CE. Expenditure estimates at the basic item-area level would be unreliable due to sampling error without the use of statistical smoothing procedures. BLS uses two basic techniques to minimize the variance associated with each basic item-area base-period expenditure estimate. First, data are pooled over an extended period in order to build the expenditure estimates on an adequate sample size. The current reference period ![]() uses 24 months of data.3 Second, basic item-area expenditures are averaged, or composite estimated, with item-regional expenditures.4 This has the effect of lowering the variance of each basic item-area expenditure at the cost of biasing it toward the expenditure patterns observed in the larger geographical area. This process is summarized in the equations in exhibit 2.
uses 24 months of data.3 Second, basic item-area expenditures are averaged, or composite estimated, with item-regional expenditures.4 This has the effect of lowering the variance of each basic item-area expenditure at the cost of biasing it toward the expenditure patterns observed in the larger geographical area. This process is summarized in the equations in exhibit 2.
Exhibit 2. Estimation of CPI-U basic aggregation weights
![]() = expenditure on item i in area a by population p in year
= expenditure on item i in area a by population p in year ![]()
![]() = total expenditures in area a by population p in year
= total expenditures in area a by population p in year ![]()
![]() = share of total expenditures for item i in area a for population p in year
= share of total expenditures for item i in area a for population p in year ![]()
![]() = expenditure on item i in major area m by population p in year
= expenditure on item i in major area m by population p in year ![]()
![]() total expenditures in major area m by population p in year
total expenditures in major area m by population p in year ![]()
![]() = share of total expenditures for item i in major area m for population p in year
= share of total expenditures for item i in major area m for population p in year ![]()
![]() = composite-estimated share of total expenditures for item i in area a
= composite-estimated share of total expenditures for item i in area a
for population p in year ![]()
![]() = estimated expenditure on item i in area a by population p in year
= estimated expenditure on item i in area a by population p in year ![]()
![]() = raked expenditures on item i in area a by population p in year
= raked expenditures on item i in area a by population p in year ![]()
![]() = estimated expenditure in expenditure reference period
= estimated expenditure in expenditure reference period ![]()
![]() = cost weight in pivot month v
= cost weight in pivot month v
![]() = aggregation weight
= aggregation weight
where
![]() = population (all urban consumers or urban wage-earners and clerical workers);
= population (all urban consumers or urban wage-earners and clerical workers);
![]() = CPI basic area;
= CPI basic area;
![]() = CPI basic item;
= CPI basic item;
![]() = expenditure class;
= expenditure class;
![]() = one of eight major areas, defined by census region and city-size classification (self-representing and non-self-representing);
= one of eight major areas, defined by census region and city-size classification (self-representing and non-self-representing);
![]() = price;
= price;
![]() = quantity;
= quantity;
![]() = number of years in the CPI-U expenditure reference period (currently, N = 2);
= number of years in the CPI-U expenditure reference period (currently, N = 2);
![]() = year belonging to expenditure reference period
= year belonging to expenditure reference period ![]() ;
;
![]() = the reference period of the expenditures used to derive the implicit quantity weights for aggregation;
= the reference period of the expenditures used to derive the implicit quantity weights for aggregation;
![]() = weight assigned to major area m, where
= weight assigned to major area m, where ![]() ;
;
![]() = lower level index base period;
= lower level index base period;
![]() = year and month, usually December, prior to the month when expenditure weights from the reference weights from reference period
= year and month, usually December, prior to the month when expenditure weights from the reference weights from reference period ![]() are first used;
are first used;
![]() = estimated expenditures PQ for item i in area a for population p in area a in period
= estimated expenditures PQ for item i in area a for population p in area a in period ![]() ;
;
![]() = lower level index of price change from index base period
= lower level index of price change from index base period ![]() to expenditure reference period
to expenditure reference period ![]() for item i in area a; and
for item i in area a; and
![]() = lower level index of price change from index base period
= lower level index of price change from index base period ![]() to pivot month v for item i in area a.
to pivot month v for item i in area a.
The estimated expenditure ![]() for item I in area a for population p in reference period
for item I in area a for population p in reference period ![]() is derived from a weighted average of the item’s relative importance in the basic area a and its relative importance in its corresponding region-size classification m, for each year encompassing reference period
is derived from a weighted average of the item’s relative importance in the basic area a and its relative importance in its corresponding region-size classification m, for each year encompassing reference period ![]() . The weight ẟ
. The weight ẟ![]() assigned to region-size class m and the weight 1–δ assigned to the basic area a are a function of the variance in each area and the covariance of each measure.5 The resulting average share
assigned to region-size class m and the weight 1–δ assigned to the basic area a are a function of the variance in each area and the covariance of each measure.5 The resulting average share ![]() is then multiplied by the sum of all expenditures in the basic area in the corresponding year to obtain a revised item expenditure. In a process called raking, the revised item expenditures are adjusted by a factor such that, once summed, they equal the unadjusted expenditures at the region-size class m expenditure class e level. Annual item-area expenditures in year
is then multiplied by the sum of all expenditures in the basic area in the corresponding year to obtain a revised item expenditure. In a process called raking, the revised item expenditures are adjusted by a factor such that, once summed, they equal the unadjusted expenditures at the region-size class m expenditure class e level. Annual item-area expenditures in year ![]() have a lower bound of $0.01. The raked item expenditures in each year of reference period
have a lower bound of $0.01. The raked item expenditures in each year of reference period ![]() are then averaged to obtain the aggregation weight: an expenditure value with an implicit price of period
are then averaged to obtain the aggregation weight: an expenditure value with an implicit price of period ![]() and implicit quantity of period
and implicit quantity of period ![]() .
.
The initial version of the C-CPI-U is published simultaneously with the CPI-U, so it uses expenditure data from the same expenditure reference period ![]() as the CPI-U for its aggregation weights. Since 2015, BLS has issued four preliminary estimates of the C-CPI-U, by quarter, with final data being published approximately 1 year after the reference month. Hence, if the ensuing year was one in which the weight was updated, then the interim version of each monthly C-CPI-U was based on more contemporaneous expenditures than its initial version. For example, 2015 initial indexes produced in 2015 used
as the CPI-U for its aggregation weights. Since 2015, BLS has issued four preliminary estimates of the C-CPI-U, by quarter, with final data being published approximately 1 year after the reference month. Hence, if the ensuing year was one in which the weight was updated, then the interim version of each monthly C-CPI-U was based on more contemporaneous expenditures than its initial version. For example, 2015 initial indexes produced in 2015 used ![]() = 2011–12. However, 2015 interim indexes produced in 2016 were constructed using
= 2011–12. However, 2015 interim indexes produced in 2016 were constructed using ![]() = 2013–14.
= 2013–14.
For the C-CPI-U, which uses the Törnqvist index formula for upper level aggregation in a monthly chained construct, monthly expenditure estimates for each basic item-area combination are required as aggregation weights. These are derived from the same CE data as the CPI-U aggregation weights. Like the biennial data used for CPI-U aggregation, adequacy of the underlying sample size from which the expenditure weights are estimated is an issue for C-CPI-U aggregation. To minimize the variance of the basic item-area monthly expenditures, a ratio-allocation procedure is adopted to estimate each item-area monthly expenditure from U.S. monthly item expenditures.
Estimated monthly expenditures are given by
![]()
where
p = population (note that C-CPI-U is produced only for the all urban consumers population),
a = CPI basic area,
i = CPI basic item,
A = all CPI basic areas (U.S. city average),
P = price,
Q = quantity,
t = month, and
T = period covering month t and 11 months prior to month t.
The monthly expenditure for an item in a basic area is derived in two steps. First, the monthly expenditure for the item is summed across all 32 areas to obtain a U.S. monthly item expenditure. Second, the U.S. monthly item expenditure is allocated among all 32 basic areas, according to each area’s relative expenditure share for the item during the current and preceding 11 months. Note that:
![]()
The estimated monthly item-area expenditures have a lower bound of $0.000833 (1/12 of a cent), and when summed over the calendar year, they have a lower bound of $0.01, which is equivalent to that of the annual data in the CPI-U expenditure reference period.
A modified Laspeyres price index is used to aggregate basic indexes into published CPI-U and CPI-W indexes. The Laspeyres index uses estimated quantities from the predetermined expenditure reference period ![]() to weight each basic item-area index. These quantity weights remain fixed for a 2-year period, and then are replaced in January of each even-numbered year when the aggregation weights are updated. In a Laspeyres aggregation, consumer substitution between items is assumed to be zero. The aggregate index for any given month is computed as a quantity-weighted average of the current month’s index divided by the index value in the index base period. Month-to-month price change is then calculated as a ratio of the long-term monthly indexes. The relevant equations follow.
to weight each basic item-area index. These quantity weights remain fixed for a 2-year period, and then are replaced in January of each even-numbered year when the aggregation weights are updated. In a Laspeyres aggregation, consumer substitution between items is assumed to be zero. The aggregate index for any given month is computed as a quantity-weighted average of the current month’s index divided by the index value in the index base period. Month-to-month price change is then calculated as a ratio of the long-term monthly indexes. The relevant equations follow.
Long-term price change is given by
![]()
Month-to-month price change is given by
![]()
where
A = all basic areas (U.S. city average),
a = CPI basic area,
p = populations (all urban consumers or urban wage earners and clerical workers),
i = CPI basic item,
I = all basic items,
t = month,
z = base period of the aggregate index (the CPI-U U.S. city average index series for all items has a base period of 1982–84),
![]() = base period of the basic index for item i in area a,
= base period of the basic index for item i in area a,
![]() = the reference period of the expenditures used to derive the implicit quantity weights needed for aggregation,
= the reference period of the expenditures used to derive the implicit quantity weights needed for aggregation,
v = pivot month (usually December) prior to the month when expenditure weights from period ![]() are first used in the CPI,
are first used in the CPI,
![]() = lower level index of price change from period
= lower level index of price change from period ![]() to month t for item i in area a for population p,
to month t for item i in area a for population p,
![]() = lower level index of price change from period
= lower level index of price change from period ![]() to pivot month v for item i in area a for population p,
to pivot month v for item i in area a for population p,
![]() = aggregation weight from reference period
= aggregation weight from reference period ![]() for item i in area a for population p,
for item i in area a for population p,
![]() = aggregate level CPI series of price change from period z to pivot month v for aggregate area i in aggregate area a for population p,
= aggregate level CPI series of price change from period z to pivot month v for aggregate area i in aggregate area a for population p,
![]() = index calculated using a Laspeyres formula, and
= index calculated using a Laspeyres formula, and
![]() = index calculated using a geometric mean formula.
= index calculated using a geometric mean formula.
In contrast, the C-CPI-U is built by chaining together indexes of 1-month price changes. For the final C-CPI-U index, each monthly index is computed using the Törnqvist formula with monthly weights from both the current and the previous month. Consumer substitution behavior is not assumed by the Törnqvist formula; rather, it is implicitly accounted for by use of current- and base-month expenditures. An index of 1-month price change is calculated and then multiplied by the index value for the previous month to obtain the current-month index value. Following are the relevant equations.
Long-term price change is given by
![]()
and month-to-month price change is given by
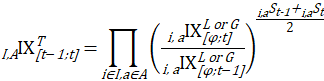
where
A = all basic areas (U.S. city average),
a = CPI basic area,
i = CPI basic item,
I = all basic items,
t = month,
z = base period of the aggregate index (the C-CPI-U U.S. city average index series for all items has a base period of December 1999),
![]() = base period of the basic index for item i in area a,
= base period of the basic index for item i in area a,
![]() = lower level index of price change from period
= lower level index of price change from period ![]() to month t for item i in area a,
to month t for item i in area a,
![]() = lower level index of price change from period
= lower level index of price change from period ![]() to month t–1 for item i in area a,
to month t–1 for item i in area a,
![]() = expenditure in month t for item i in area a as a percentage of total expenditures in month t for aggregate item i in aggregate area A,
= expenditure in month t for item i in area a as a percentage of total expenditures in month t for aggregate item i in aggregate area A,
![]() = expenditure in month t–1 for item i in area a as a percentage of total expenditures in month t–1 for aggregate item i in aggregate area A, and
= expenditure in month t–1 for item i in area a as a percentage of total expenditures in month t–1 for aggregate item i in aggregate area A, and
![]() = aggregate level C-CPI-U Törnqvist index of price change from period z to month t for aggregate item i in aggregate area A.
= aggregate level C-CPI-U Törnqvist index of price change from period z to month t for aggregate item i in aggregate area A.
BLS revises the C-CPI-U quarterly, using the constant elasticity of substitution formula for the calculation of the preliminary versions of that index. The initial version of the C-CPI-U is released concurrently with the CPI-U for each calendar month. The final version of the index is released approximately 10-12 months later. In between the initial release and the final release, there are three quarterly updates. The 1-month price change for each interim release is the same as the initial version. The interim versions reflect only updates to index levels—that is, the value of the index in a given month relative to the value in its base period. These updates result from the conversion of 1-month price changes from initial to final value in preceding months in the monthly chained series. The constant elasticity of substitution uses an estimate of consumer substitution that lies between the estimates assumed in the geometric mean and Laspeyres formulas, and represents a model that is closer to actual consumer behavior. This estimate of consumer substitution σ is called the elasticity of substitution. For additional information on the C-CPI-U framework, see the article Improving initial estimates of the Chained Consumer Price Index.
Month-to-month price change under the constant elasticity of substitution formula is given by:
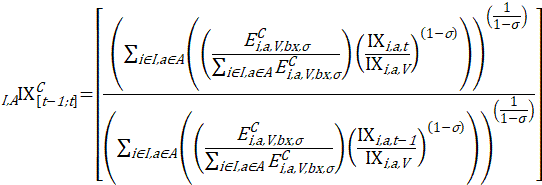
The constant elasticity of substitution pivoted expenditure weight for a biennial period is given by:
![]()
where
A = all basic areas (U.S. city average),
a = CPI basic area,
i = CPI basic item,
I = all basic items,
t = month,
b = biennial expenditure reference period,
x = index base period (initially December 1999 = 100),
V = pivot month,
![]() = price of item i in area a during period b,
= price of item i in area a during period b,
![]() = quantity of item i in area a during period b,
= quantity of item i in area a during period b,
σ = elasticity of substitution for the index period, and
![]() = lower level index for item i in area a in month t.
= lower level index for item i in area a in month t.
Seasonal adjustment removes the estimated effect of changes that normally occur at the same time every year, such as price movements resulting from changing climatic conditions, production cycles, model changeovers, holidays, and sales. CPI series are selected for seasonal adjustment if they pass certain statistical criteria and if there is an economic rationale for the observed seasonality. Seasonal factors used in computing the seasonally adjusted indexes are derived using X-13ARIMA-SEATS seasonal adjustment software. In some cases, intervention analysis seasonal adjustment is carried out using X-13ARIMA-SEATS to derive more accurate seasonal factors. Consumer price indexes may be adjusted directly or aggregately, depending on the level of aggregation of the index and the behavior of the component series.6
Some index series show erratic behavior due to nonseasonal economic events (called interventions) or methodology changes. These events, which can be one-time occurrences or recurring events that happen at infrequent and irregular intervals, adversely affect the estimate of the seasonal component of the series.
Intervention analysis seasonal adjustment allows nonseasonal economic phenomena, such as outliers and level shifts, to be factored out of indexes before calculation of seasonal adjustment factors. (An outlier is an extreme value for a particular month. A level shift is a change or shift in the price level of a CPI series caused by an event, such as an excise tax increase or oil embargo, occurring over 1 or more months.) An index series whose underlying trend has experienced a sharp and permanent shift will generate distorted results when adjusted using the standard X-13ARIMA-SEATS procedure. The X-13ARIMA-SEATS regression techniques are used to model the distortions and account for them as part of the seasonal adjustment process. The result is an adjustment based on a representation of the series with the seasonal pattern emphasized. Intervention analysis seasonal adjustment also makes it possible to account for seasonal shifts, resulting in better seasonal adjustment in the periods before and after the shift occurred. Not all CPI series are adjusted using intervention analysis seasonal adjustment techniques. These seasonal factors are applied to the original unadjusted series. Level shifts and outliers, removed in calculating the seasonal factors, remain in the resulting seasonally adjusted series.
In recent years, BLS has used intervention analysis seasonal adjustment for various indexes, such as gasoline, fuel oil, new vehicles, women’s and girls’ apparel, educational books and supplies, electricity, utility (piped) gas service, water and sewerage maintenance, nonalcoholic beverages and beverage materials, and whiskey at home. Series are adjusted using intervention analysis techniques when interventions are clearly identified. After a number of years, series may revert to adjustment using standard methods. For some series, intervention analysis is used and the resulting series does not show a clear and stable seasonal pattern. In these cases, the series is not seasonally adjusted.
Each year, BLS seasonally adjusts eligible lower-level CPI index series directly with the X-13ARIMA-SEATS software using unadjusted indexes for the latest 5 to 8 calendar years. CPI index series are adjusted using the multiplicative model. Most high-level index series are adjusted by the aggregative method, which is more appropriate for broad categories whose component indexes show strongly different seasonal patterns. Under the aggregative method, direct adjustment is first applied to indexes at lower levels of detail, and thereafter the adjusted detail is aggregated to yield the higher level seasonally adjusted indexes. If intervention analysis is indicated, it will be used in adjusting selected lower level indexes prior to aggregation. For those series that have not been selected for seasonal adjustment, the original unadjusted data are used in the aggregation process.
The seasonal factors are updated annually. Each year in February, BLS recalculates and publishes revised seasonally adjusted indexes for the previous 5 years. Seasonally adjusted indexes become final in the 5th and last year of revision. Seasonal factors for the past year are used to generate seasonally adjusted indexes for the current year starting with the release of the January CPI.
CPI annual average indexes use 12 successive months of CPI values:
![]()
Semiannual average indexes are computed for the first half of the year (January to June) and for the second half of the year (July to December) using 6 successive months of CPI values:
![]()
For bimonthly indexes, the intermediate indexes are calculated using a geometric mean of the values in the months adjacent to the one being estimated.
Average prices are estimated from CPI data for selected food and beverage items, utility (piped) gas, electricity, gasoline, automotive diesel fuel, and fuel oil number 2 to support the research and analytic needs of CPI data users. (See appendix 6.) Average food prices are published without tax, while the other average prices are published with tax included.
All eligible prices are converted to a price per normalized quantity. These prices are then used to estimate a price for a defined fixed quantity. For example, prices for a variety of package sizes for flour are converted to prices per ounce. An average price per ounce of flour is then estimated and multiplied by 16 to yield a price per pound, the published quantity.
The average price for collection period t is estimated as
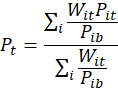
where
![]() the quote-level expenditure weight of items used in the average price estimation for the ELI/PSU/replicate in time period t,
the quote-level expenditure weight of items used in the average price estimation for the ELI/PSU/replicate in time period t,
![]() the price of item i in the base period,
the price of item i in the base period,
![]() the price of item i in period t, and
the price of item i in period t, and
![]() the average price for period t.
the average price for period t.
Dividing the expenditure weight by the base price for a given quote yields an implicit estimate of quantity. Thus, the average price is conceptually a weighted average of prices, where the weights are quantity amounts. Imputed prices are used in estimating average prices.
An important advantage of probability sampling methods is that a measure of the sampling error of survey estimates can be computed directly from the sample data. The CPI sample design accommodates error estimation by making two or more selections (replications) of items and outlets within an index area. Therefore, two or more samples of quotes in each self-representing PSU and one in each non-self-representing PSU are available. With this structure, which reflects all stages of the sample design, variance estimation techniques using replicated samples can be used.
We divide the total error into two sources: sampling error and nonsampling error. Sampling error is the uncertainty in the CPI caused by the fact that a sample of retail prices is used to compute the CPI, instead of using the complete universe of retail prices. The sampling variance attributable to the estimation of expenditure weights is not directly incorporated in the variance estimates computed for the CPI.7 Research suggests that the impact of CE sample sizes is on the variance of the variance and not on the expected value of the variance of CPI estimates. Nonsampling error is the rest of the error, and will be discussed at the end of this section. Incorrect information given by survey respondents and data processing errors are examples of nonsampling error.
BLS constantly tries to improve the precision of the CPI. Variance and sampling error are reduced by using samples of retail prices that are as large as possible, given resource constraints. BLS has developed a model that optimizes the allocation of resources. The model indicates the number of prices that should be observed in each geographic area and each item category to minimize the variance of the U.S. city average all-items index. BLS reduces nonsampling error through a series of computerized and professional data reviews, as well as through continuous survey process improvements and theoretical research.
Starting in 1978, the CPI’s sample design has accommodated variance estimation by using two or more independent samples of items and outlets in each geographic area. This allows two or more statistically independent estimates of the index to be made. The independent samples are called replicates, and the set of all observed prices is called the full sample.
As discussed earlier, BLS calculates indexes for 32 geographic areas across the United States. The 32 areas consist of 23 self-representing areas and 9 non-self-representing areas. Self-representing areas are large metropolitan areas, such as the Boston and the San Francisco metropolitan areas. Non-self-representing areas are collections of smaller metropolitan areas. For example, one non-self-representing area is a collection of 64 small metropolitan areas in the Middle Atlantic division (Pittsburgh, Buffalo, Rochester, Reading, and others) of which four metropolitan areas have been randomly selected to represent the entire set. Within each of the 32 areas, price data are collected for 243 basic item categories. Together, the 243 basic item categories cover all consumer purchases.
Multiplying the number of areas (32) by the number of item strata (243) gives 7,776 different item-area combinations for which price indexes need to be calculated. Separate price indexes are calculated for each one of these 7,776 item-area combinations. After calculating all 7,776 of these basic level indexes, the indexes are then aggregated to form higher level indexes, using expenditure estimates from the CE as their weights.
CPI variances are primarily computed with a stratified random groups method, for 1-, 2-, 6- and 12-month percent changes. Since 1998, BLS uses the stratified random groups method, in which replicate percent change estimates are computed separately for certain subsets of areas by substituting replicate cost weights for full sample cost weights, and then those individual percent change estimates are subtracted from the full sample percent change estimate and squared. These estimates are combined to produce the variance of the entire item-area combination.
Let IX(A,I,f,t) denote the index value for area A, item category I, in month t, where f indicates that it is the full sample value, and let IX(A,I,f,t–k) denote the value of the same index in month t–k. The uppercase letter A denotes a set of areas, such as the Northeast or Midwest region of the country, and the uppercase letter I denotes a set of item strata, such as all items or all items less food and energy, or a single item stratum. Also, let IX(A,I,r,t) and IX(A,I,r,t–k) be the corresponding index values for replicate r. Most areas have two replicates, but some have more.
Then the full-sample k-month percent change between months t–k and t is computed by dividing IX(A,I,f,t) by IX(A,I,f,t–k), subtracting 1, and multiplying by 100:
![]()
where
![]() = full-sample k-month percent change between months t–k and t, for item category I in area A;
= full-sample k-month percent change between months t–k and t, for item category I in area A;
IX(A,I,f,t) = index value for area A, item category I, for the full sample, in month t;
IX(A,I,f,t–k) = index value for area A, item category I, for the full sample, in month t–k;
A= area;
I = item category;
t = month;
t–k = month k months before month t;
f = subscript indicating that the value is for the full sample; and
r = parameter indicating that the value is for a replicate.
Every index has an aggregation weight AGGWT(A, I, f ) or AGGWT(A, I, r ) associated with it, which is used to combine the index with others to produce aggregate indexes for larger geographic areas and larger item categories. For example, the aggregation weights are used to combine all 7,776 basic-level indexes into higher level indexes such as the U.S. city average all-items index.
The product of an index and its weight is called a cost weight:
![]()
where
CW(A,I,f,t) = cost weight for area A, item category I, for the full sample, in month t;
IX(A,I,f,t) = index value for area A, item category I, for the full sample, in month t;
AGGWT(A,I,f,t) = aggregation weight for area A, item category I, for the full sample, in month t;
A= area;
I = item category;
t = month; and
f = parameter indicating that the value is for the full sample.
A cost weight is an estimate of the total cost in area A for consumption of item category I in month t. Replicate cost weights are produced from replicate level indexes and full sample aggregation weights. Because the aggregation weights are not indexed by time (except across pivot months; see the section below, “Bridging across pivot months”), the preceding percent change formula is equivalent to:
![]()
where
![]() = full-sample k-month percent change between months t–k and t, for item category I in area A;
= full-sample k-month percent change between months t–k and t, for item category I in area A;
![]() = cost weight for area A, item category I, for the full sample, in month t;
= cost weight for area A, item category I, for the full sample, in month t;
![]() = cost weight for area A, item category I, for the full sample, in month t–k;
= cost weight for area A, item category I, for the full sample, in month t–k;
A= area;
I = item category;
t = month;
t–k = month k months before month t; and
f = parameter indicating that the value is for the full sample.
which is equivalent to:
![]()
because cost weights are additive from the lowest area-item level up to the highest U.S. city average all items level. The lowercase letter a denotes 1 of the 32 basic-level areas included in area = A, and the lowercase letter i denotes 1 of the 243 item categories. (Note: Item aggregation I can be as small as one item stratum or may comprise one or more major groups.)
For the Stratified Random Groups method used here, replicate percent changes are defined as follows: full sample cost weights are used for every geographic area within area = A except for one of the areas. In the omitted area, the full sample cost weight is replaced by a replicate cost weight. Let the lowercase letter a denote 1 of the 32 basic-level areas included in area = A.
Then, the replicate percent change, for area = a, item = I, replicate = r, between months t–k and t, is computed as:
![]()
where
![]()
![]() = replicate k-month percent change between months t–k and t, for item category I in area A;
= replicate k-month percent change between months t–k and t, for item category I in area A;
a = basic area;
A = aggregate area;
I = item;
r = parameter indicating that the value is for a replicate;
f = parameter indicating that the value is for the full sample;
t = month;
t–k = month k months before month t; and
![]() cost weight in area A of item category I.
cost weight in area A of item category I.
The variance is computed with the following stratified random groups variance estimation formula:
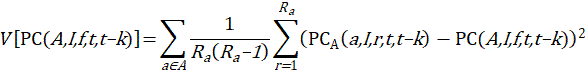
where
![]() = the variance of the full sample k-month percent change between months t–k and t, for item category I in area A;
= the variance of the full sample k-month percent change between months t–k and t, for item category I in area A;
![]() = replicate k-month percent change between months t–k and t, for item category I in area A;
= replicate k-month percent change between months t–k and t, for item category I in area A;
![]() = full-sample k-month percent change between months t–k and t, for item category I in area A;
= full-sample k-month percent change between months t–k and t, for item category I in area A;
a = basic area;
A = aggregate area;
I = item;
r = parameter indicating that the value is for a replicate;
f = parameter indicating that the value is for the full sample;
t = month;
t–k = month k months before month t; and
![]() = the number of replicates in area a.
= the number of replicates in area a.
Finally, the standard error of the percent change is computed by taking the square root of its variance:
![]()
where
![]() the standard error of the full sample k-month percent change between months t–k and t, for item category I in area A;
the standard error of the full sample k-month percent change between months t–k and t, for item category I in area A;
![]() = the variance of the full sample k-month percent change between months t–k and t, for item category I in area A;
= the variance of the full sample k-month percent change between months t–k and t, for item category I in area A;
![]() = replicate k-month percent change between months t–k and t, for item category I in area A;
= replicate k-month percent change between months t–k and t, for item category I in area A;
![]() = full-sample k-month percent change between months t–k and t, for item category I in area A;
= full-sample k-month percent change between months t–k and t, for item category I in area A;
a = basic area;
A = aggregate area;
I = item;
r = parameter indicating that the value is for a replicate;
f = parameter indicating that the value is for the full sample;
t = month; and
t–k = month k months before month t.
BLS publishes index series for 82 special relative (item) categories (SRCs), which are below the item stratum level and thus do not have accompanying replicate index values. (CE weights are produced only down to the item-stratum level in each index area.) The CPI stratified random groups methodology requires a replicate structure. So, for these SRC items (such as butter or pork or new cars), an alternative variance estimation method is needed. Given the availability (at the regional and higher area levels) of independent estimates for these SRC items, the jackknife variance estimation methodology can be employed. Each area’s full-sample cost weight can be subtracted from the all-area full-sample cost weight to provide a jackknife replicate estimate. By taking the ratio of these replicate cost weight estimates at times t and t–k, subtracting 1, and multiplying by 100, one obtains the required jackknife replicate percent change value. (For the U.S. city average special item estimates, there are 32 independent index areas, and so there are 32 jackknife replicate estimates with which to work.)
The full-sample percent change is computed as before (except that, here, item category = I is smaller even than an item stratum):
![]()
where
![]() = full-sample k-month percent change between months t–k and t, for item category I in area A;
= full-sample k-month percent change between months t–k and t, for item category I in area A;
![]() = cost weight for area A, item category I, for the full sample, in month t;
= cost weight for area A, item category I, for the full sample, in month t;
![]() = cost weight for area A, item category I, for the full sample, in month t–k;
= cost weight for area A, item category I, for the full sample, in month t–k;
A= area;
I = item category;
t = month;
t–k = month k months before month t; and
f = parameter indicating that the value is for the full sample.
The jackknife replicate percent change is computed as follows:
![]()
Then the variance for the k-month percent change is computed in the usual jackknife form:
![]()
Every 2 years, BLS updates its set of aggregation index weights based on CE data collected from the t–2 and t–3 years. In January 2016, BLS replaced its old set of aggregation weights with a new 2-year set of weights from expenditure data collected in 2013–14. In January 2018, this set of weights was replaced by an updated set of weights from expenditure data collected in 2015–16, and so on.
Whenever the variance estimates cross the pivot month (as they did in December 2015 and December 2017), a bridging factor has to be introduced into any variance calculation that crosses the pivot month anywhere between t and t–k months (including month t–k, but not including month t ). The bridging factor is then applied directly to the individual ratio of cost weights, for both full-sample and replicate values, inside each percent change calculation.
Thus, in its most general form:
![]()
for every combination of area and item, and for full-sample and replicate values, with the bridging factor defaulting to 1 whenever not applicable.
The bridging factor essentially allows the old aggregation weight in the bridge’s numerator to cancel out the old aggregation weight in the t–k cost weight, while the new aggregation weight in the bridge’s denominator cancels out the new aggregation weight in the t cost weight, leaving the index relative free to move this level’s percent change without disruption.
where
![]() = bridging factor,
= bridging factor,
![]() = old cost weight,
= old cost weight,
![]() = new cost weight,
= new cost weight,
![]() = month, and
= month, and
![]() = the month that is k months before month t.
= the month that is k months before month t.
Surveys involve many operations, all of which are potential sources of nonsampling error. The errors arise from the survey process, regardless of whether the data are collected from the entire universe or from a sample of the population. The most general categories of nonsampling error are coverage error, nonresponse error, response error, processing error, and estimation error.
Coverage error in an estimate results from the omission of part of the target population (undercoverage) or the inclusion of units from outside of the target population (overcoverage). Such errors arise from the omission of cities, households, outlets, and items that are part of the target populations from the relevant sampling frames or from their double-counting or improper inclusion in the frames. A potential source of coverage error is the time lag between the Consumer Expenditure Survey (CE) and the initiation of price collection for commodities and services at sampled outlets. Because of the time lag, the products offered by the outlet at the time pricing is initiated may not coincide with the set from which the CE respondents were purchasing.
Nonresponse error results when data are not collected for some sampled units because of the failure to interview households or outlets. This can occur when selected households and outlets cannot be contacted or refuse to participate in the survey. Response rates during monthly pricing for the CPI C&S and housing surveys are published annually and available online.
Response error results from the collection and use of incorrect, inconsistent, or incomplete data during estimation. Response error may arise because of the collection of data from inappropriate respondents, respondent memory or recall errors, deliberate distortion of responses, interviewer effects, misrecording of responses, pricing of wrong items, misunderstanding or misapplication of data collection procedures, or misunderstanding of the survey needs and/or lack of cooperation from respondents. The pricing methodology in the commodities and services component of the CPI allows the previous period’s price to be available at the time of collection. This dependent pricing methodology is believed to reduce response variance for measuring change, but may cause response bias and lag. The housing component of the CPI employs an independent pricing methodology specifically to avoid potential response bias.
Processing error arises from incorrect editing, coding, and data transfer. Price data are collected by computer-assisted data collection. Automated data checking ensures that only correct data types are collected; other automated logic checks remove all redundant question patterns, and the instrument informs staff when not all required data have been collected. Errors can also result from software problems in the computer processing that cause correctly entered data to be lost. Computer screening and professional review of the data provide checks on processing accuracy. Studies of these processing errors in the CPI have shown them to be extremely small.
Estimation error results when the survey process does not accurately measure what it is intended to measure. Such errors may be conceptual or procedural in nature, arising from a misunderstanding of the underlying survey measurement concepts or a misapplication of rules and procedures.
Substitutions and adjustments for quality change in the items priced for the CPI are possible sources of estimation error due to procedural difficulties. Ideally, CPI data collection forms and procedures would yield all information necessary to determine or explain price and quality differences for all items defined within an ELI. Because such perfect information is not available, BLS economists supplement directly collected data with secondary data. Estimation error will result, if the BLS adjustment process—which may require significant judgment or lack key data—is misapplied, or if it consistently overestimates or underestimates quality change for particular kinds of items.
The effect of the aging of housing units is an example of potential estimation error, which is similar to the issue of quality change in commodities and services. In 1988, BLS began adjusting for the slow depreciation of houses and apartments over time. BLS research indicates that annual changes in the residential rent and owners’ equivalent rent indexes would have been 0.1 to 0.2 percent larger if some type of aging adjustment had been included.
The total nonsampling error of the CPI results from errors in the type of data collected, the methods of collection, the data processing routines, and the estimation processes. The cumulative nonsampling error can be much greater than the sampling error.
Response rates are calculated for the CPI at the data collection phase and at the index estimation phase for ongoing pricing. The response rate at the data collection phase is the number of responding sample units divided by the sum of the number of eligible sample units and the number of sample units with eligibility not determined. A sample unit is eligible if it belongs to the defined target population and responses should be collected from the unit for one or more items. The response rate at estimation is defined as the number of sample units used in estimation divided by the sum of the number of eligible sample units and the number of sample units with eligibility not determined.
Commodities and services items (except rent and owner’s equivalent rent) are further broken down into outlets and quotes. An outlet is a generic term used to describe places where prices are collected. A quote is a specific item to be priced in a specific outlet. There may be from 1 to more than 50 quotes priced in an outlet. Relatively low percentages of quotes are reported collected and reported used in apparel estimation. Low rates for these items can mostly be attributed to the design of the apparel sample. Because apparel items are commonly in stores only at certain times of the year, most of the apparel sample is doubled, with each half of the sample designated for pricing during part of the year. Thus, at any particular time of the year many apparel quotes, although eligible, are designated “out of season,” and prices are not collected. For additional information, see the earlier subsection on seasonal items.
The response rates for housing (shelter) include categories for rental units only; owner-occupied housing units are out of scope for the CPI housing sample. A unit qualifies for inclusion if its tenure status is known either by previous knowledge or is collected in the current interview period. The response rates at the data collection phase for housing (shelter) are separated into three categories. If usable information is obtained, the unit is designated eligible and the data are reported. If the assigned unit is located but is unoccupied, the unit is designated “eligible, found vacant.” In instances where the unit is eligible but no data are available (for example refusals), the unit is designated “eligible, other.” The response rates at the estimation phase are units that are used in either rent or rental equivalence.
[1] For more information on vacancy imputation, see J.P. Sommers and J.D. Rivers, “Vacancy imputation methodology for rents in the CPI,” Proceedings of the American Statistical Association, Business and Economic Statistics Section (Alexandria, VA: American Statistical Association, 1983).
[2] For further information, see Walter F. Lane, William C. Randolph, and Stephen A. Berenson, “Adjusting the CPI shelter index to compensate for effect of depreciation,” Monthly Labor Review, October 1988, pp. 34–37.
[3] Prior to 2002, the expenditure reference period was based on 36 months of data (for example, ![]() = 1993–95 from 1998 to 2001 and
= 1993–95 from 1998 to 2001 and ![]() = 1982–84 from 1987 to 1997).
= 1982–84 from 1987 to 1997).
[4] Basic areas are grouped into city-size classifications by region for the purpose of composite estimation. There are four regions (Northeast, Midwest, South, and West) and two city-size classifications (A-sized cities and non-A-sized cities) for a total of eight regional city-size classifications.
[5] For more information on composite estimation, see Michael P. Cohen and John P. Sommers, “Evaluation of the methods of composite estimation of cost weights for the CPI,” Proceedings of the American Statistical Association, Business and Economic Statistics Section (Alexandria, VA: American Statistical Association, 1984.), pp. 466–471.
[6] J.A. Buszuwski and S. Scott, "On the use of intervention analysis in seasonal adjustment,'' Proceedings of the American Statistical Association, Business and Economics Section (Alexandria, VA, American Statistical Association, 1988).
[7] See the U.S. Bureau of Labor Statistics Consumer Expenditure Survey Methodology for more detail on consumer expenditure weights, https://www.bls.gov/opub/hom/cex/calculation.htm.