An official website of the United States government
 United States Department of Labor
United States Department of Labor

Crossref 0
Higher-Level Aggregation Using Long-Term Links in the Swedish CPI, Journal of Official Statistics, 2025.
Retrospective Computations of Price Index Numbers: Theory and Application, Review of Income and Wealth, 2024.
Substitution Bias in Multilateral Methods for CPI Construction Using Scanner Data, SSRN Electronic Journal, 2018.
Revisiting taste change in cost-of-living measurement, Journal of Economic and Social Measurement, 2022.
In January 2015, the U.S. Bureau of Labor Statistics (BLS) implemented two improvements to the Chained Consumer Price Index for All Urban Consumers (C-CPI-U). First, the revision schedule of the index series was changed from an annual revision to a quarterly revision. As a result of the more frequent revisions, the lag between the initial and final publication of each monthly index was reduced by an average of 11 months.1 Second, and the focus of this article, the index formula used to calculate the initial version of the index was changed from an adjusted Geometric Young formula to a constant elasticity of substitution (CES) formula. The new formula was implemented to more closely approximate the final indexes than the previous Geometric Young formula.
The objective of the BLS Consumer Price Index (CPI) is to approximate a cost-of-living index (COLI). This is accomplished by addressing the following question: What is the cost, at the current month’s market prices, of achieving the standard of living attained in the base period?2 Within the context of consumer utility-maximization behavior, this cost represents the change in spending needed to attain a constant level of consumer satisfaction when faced with prices in future periods that differ from those in the base period. The headline Consumer Price Index for All Urban Consumers (CPI-U) assumes that consumers respond to price change by purchasing the same quantities as in the past and does not reflect consumer substitution in response to relative price change for a defined biennial period. The CPI-U, therefore, is an overstatement of a COLI if, within a biennial period, consumers change their consumption patterns in response to changing relative prices, like buying fewer goods at relatively higher prices and substituting with comparable goods at relatively lower prices.
In contrast to the CPI-U, the C-CPI-U, first introduced with the release of July 2002 CPI data, employs a formula that reflects the effect of substitution that consumers make across item categories in response to changes in relative prices.3 The final C-CPI-U is a superlative index 4 and is a second-order approximation of a COLI.5 The final C-CPI-U better approximates a COLI for several reasons, not the least of which is due to the weights. The weights used are derived from the current period and base period, the periods over which price change is measured. A first-order approximation like the CPI-U uses weights from only one of the periods. The monthly weights for the C-CPI-U formula directly reflect substitutions that consumers make when facing relative price change.
Prior to the release of the January 2015 CPI-U, three upper-level aggregation formulas were calculated for BLS CPI products: Lowe (used for the CPI-U and the Consumer Price Index for Urban Wage Earners and Clerical Workers), Tornqvist (used for the final C-CPI-U), and Geometric Young (used for preliminary versions of the C-CPI-U).6 Starting with the release of the January 2015 CPI-U, the Lloyd–Moulton CES formula (referred to as CES for the remainder of this article) replaced the Geometric Young formula for preliminary versions of the C-CPI-U.7 Each of these formulas use the same measure of elementary item-area price change as an input: (IXt/IXt-1). However, the expenditure weight input varies on the basis of assumption of the overall consumers’ substitution elasticity (σ). The four formulas are summarized in table 1.
The CPI-U is calculated with a Lowe fixed quantity formula, in which quantities are represented by price-updated expenditures.8 This formula assumes that substitution elasticity is zero within a biennial period, meaning consumers do not substitute across items in response to relative price change. The difference between price change estimated using fixed quantity weights and the actual quantities purchased is referred to as upper-level substitution bias in the CPI-U.
A Tornqvist formula, which includes consumer substitution using the current and previous month weights, is used to calculate final C-CPI-U. BLS is currently unable to produce the final C-CPI-U in real time because the monthly expenditure weights lags the current index period by about four quarters. This time lag is necessary to conduct and process the Consumer Expenditure Survey household data, the source of the monthly weight estimates. BLS publishes preliminary C-CPI-U indexes, designed to approximate the final C-CPI-U index, to address the time gap.
Up to the January 2015 CPI-U release, preliminary C-CPI-U indexes were estimated with a Geometric Young formula that assumes substitution elasticity to be unitary within a biennial period. The underlying assumption of this estimator implied consumers always substitute to items whose prices are falling relative to items whose prices are increasing. Since the release of the January 2015 CPI-U, the preliminary versions of the C-CPI-U have been estimated with a CES index formula, which assumes consumer substitution is constant within a biennial time period and the level of substitution is estimated by prior period behavior. The remainder of this article describes the process behind making this formula change to the preliminary C-CPI-U, and the resulting improvement. Table 1 shows the price index formula relationships among different CPI products. Figure 1 displays a comparison of index levels from these formulas with December 1999 = 100.
| Index period | Final C-CPI-U | CPI-U | Geometric Young | CES = 0.0 | CES = 0.1 | CES = 0.2 | CES = 0.3 | CES = 0.4 | CES = 0.5 | CES = 0.6 | CES = 0.7 | CES = 0.8 | CES = 0.9 | CES = 0.999 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan 2000 | 100.337 | 100.332 | 100.256 | 100.334 | 100.327 | 100.320 | 100.313 | 100.306 | 100.298 | 100.291 | 100.283 | 100.274 | 100.265 | 100.256 |
| Feb 2000 | 100.887 | 100.914 | 100.781 | 100.915 | 100.903 | 100.890 | 100.877 | 100.864 | 100.851 | 100.838 | 100.824 | 100.810 | 100.795 | 100.781 |
| Mar 2000 | 101.631 | 101.727 | 101.552 | 101.729 | 101.712 | 101.696 | 101.679 | 101.662 | 101.645 | 101.627 | 101.609 | 101.590 | 101.571 | 101.552 |
| Apr 2000 | 101.649 | 101.803 | 101.621 | 101.804 | 101.788 | 101.771 | 101.754 | 101.736 | 101.719 | 101.700 | 101.682 | 101.662 | 101.642 | 101.621 |
| May 2000 | 101.683 | 101.888 | 101.690 | 101.889 | 101.872 | 101.854 | 101.835 | 101.816 | 101.797 | 101.777 | 101.757 | 101.735 | 101.713 | 101.690 |
| Jun 2000 | 102.111 | 102.453 | 102.128 | 102.455 | 102.425 | 102.395 | 102.365 | 102.334 | 102.302 | 102.270 | 102.236 | 102.201 | 102.166 | 102.129 |
| Jul 2000 | 102.305 | 102.659 | 102.274 | 102.660 | 102.626 | 102.591 | 102.555 | 102.519 | 102.481 | 102.443 | 102.403 | 102.362 | 102.319 | 102.275 |
| Aug 2000 | 102.297 | 102.675 | 102.284 | 102.677 | 102.642 | 102.607 | 102.571 | 102.535 | 102.497 | 102.457 | 102.417 | 102.374 | 102.330 | 102.284 |
| Sep 2000 | 102.796 | 103.225 | 102.814 | 103.227 | 103.190 | 103.153 | 103.115 | 103.076 | 103.036 | 102.995 | 102.952 | 102.908 | 102.862 | 102.814 |
| Oct 2000 | 102.899 | 103.386 | 102.976 | 103.388 | 103.352 | 103.315 | 103.277 | 103.239 | 103.199 | 103.158 | 103.115 | 103.071 | 103.025 | 102.977 |
| Nov 2000 | 102.834 | 103.462 | 102.973 | 103.463 | 103.421 | 103.379 | 103.335 | 103.289 | 103.242 | 103.194 | 103.143 | 103.089 | 103.032 | 102.973 |
| Dec 2000 | 102.624 | 103.384 | 102.862 | 103.385 | 103.341 | 103.296 | 103.250 | 103.202 | 103.152 | 103.100 | 103.045 | 102.988 | 102.927 | 102.863 |
| Jan 2001 | 103.303 | 104.052 | 103.358 | 104.053 | 103.992 | 103.931 | 103.868 | 103.803 | 103.737 | 103.668 | 103.596 | 103.521 | 103.441 | 103.359 |
| Feb 2001 | 103.658 | 104.480 | 103.776 | 104.482 | 104.422 | 104.361 | 104.298 | 104.233 | 104.166 | 104.096 | 104.022 | 103.945 | 103.863 | 103.777 |
| Mar 2001 | 103.894 | 104.736 | 104.064 | 104.738 | 104.682 | 104.624 | 104.565 | 104.504 | 104.440 | 104.374 | 104.303 | 104.229 | 104.150 | 104.065 |
| Apr 2001 | 104.201 | 105.129 | 104.389 | 105.131 | 105.069 | 105.005 | 104.940 | 104.872 | 104.802 | 104.728 | 104.651 | 104.569 | 104.482 | 104.390 |
| May 2001 | 104.557 | 105.572 | 104.731 | 105.573 | 105.503 | 105.430 | 105.356 | 105.278 | 105.198 | 105.115 | 105.027 | 104.934 | 104.836 | 104.732 |
| Jun 2001 | 104.830 | 105.800 | 104.941 | 105.801 | 105.731 | 105.659 | 105.584 | 105.506 | 105.424 | 105.339 | 105.249 | 105.153 | 105.051 | 104.942 |
| Jul 2001 | 104.494 | 105.460 | 104.557 | 105.461 | 105.387 | 105.311 | 105.232 | 105.150 | 105.064 | 104.974 | 104.879 | 104.779 | 104.672 | 104.558 |
| Aug 2001 | 104.604 | 105.499 | 104.576 | 105.501 | 105.426 | 105.350 | 105.270 | 105.187 | 105.100 | 105.008 | 104.911 | 104.807 | 104.696 | 104.578 |
| Sep 2001 | 104.940 | 105.929 | 104.956 | 105.930 | 105.851 | 105.769 | 105.685 | 105.597 | 105.505 | 105.409 | 105.307 | 105.198 | 105.081 | 104.957 |
| Oct 2001 | 104.654 | 105.581 | 104.661 | 105.583 | 105.509 | 105.433 | 105.354 | 105.271 | 105.185 | 105.094 | 104.997 | 104.893 | 104.782 | 104.662 |
| Nov 2001 | 104.366 | 105.395 | 104.381 | 105.396 | 105.314 | 105.229 | 105.141 | 105.050 | 104.954 | 104.853 | 104.747 | 104.634 | 104.512 | 104.382 |
| Dec 2001 | 103.869 | 104.988 | 103.899 | 104.989 | 104.901 | 104.809 | 104.715 | 104.617 | 104.514 | 104.406 | 104.291 | 104.170 | 104.039 | 103.900 |
| Jan 2002 | 104.166 | 105.262 | 104.146 | 105.263 | 105.172 | 105.079 | 104.982 | 104.882 | 104.776 | 104.665 | 104.548 | 104.423 | 104.290 | 104.147 |
| Feb 2002 | 104.502 | 105.669 | 104.507 | 105.670 | 105.576 | 105.478 | 105.377 | 105.272 | 105.162 | 105.047 | 104.925 | 104.795 | 104.657 | 104.509 |
| Mar 2002 | 105.068 | 106.239 | 105.106 | 106.240 | 106.148 | 106.053 | 105.955 | 105.853 | 105.746 | 105.633 | 105.514 | 105.388 | 105.252 | 105.108 |
| Apr 2002 | 105.634 | 106.842 | 105.715 | 106.843 | 106.752 | 106.658 | 106.561 | 106.460 | 106.353 | 106.241 | 106.123 | 105.996 | 105.861 | 105.716 |
| May 2002 | 105.573 | 106.819 | 105.688 | 106.820 | 106.729 | 106.635 | 106.537 | 106.436 | 106.329 | 106.217 | 106.098 | 105.971 | 105.835 | 105.690 |
| Jun 2002 | 105.582 | 106.906 | 105.729 | 106.917 | 106.821 | 106.722 | 106.619 | 106.512 | 106.400 | 106.282 | 106.157 | 106.024 | 105.882 | 105.730 |
| Jul 2002 | 105.737 | 107.024 | 105.781 | 107.028 | 106.927 | 106.822 | 106.713 | 106.600 | 106.483 | 106.359 | 106.228 | 106.089 | 105.940 | 105.782 |
| Aug 2002 | 106.034 | 107.354 | 106.076 | 107.359 | 107.254 | 107.146 | 107.034 | 106.918 | 106.797 | 106.669 | 106.535 | 106.392 | 106.240 | 106.078 |
| Sep 2002 | 106.254 | 107.545 | 106.252 | 107.549 | 107.444 | 107.334 | 107.221 | 107.104 | 106.981 | 106.852 | 106.716 | 106.572 | 106.417 | 106.254 |
| Oct 2002 | 106.405 | 107.750 | 106.438 | 107.752 | 107.645 | 107.535 | 107.420 | 107.301 | 107.177 | 107.046 | 106.908 | 106.762 | 106.606 | 106.439 |
| Nov 2002 | 106.326 | 107.748 | 106.375 | 107.750 | 107.637 | 107.521 | 107.401 | 107.277 | 107.146 | 107.010 | 106.865 | 106.713 | 106.550 | 106.377 |
| Dec 2002 | 106.046 | 107.507 | 106.068 | 107.508 | 107.390 | 107.268 | 107.141 | 107.010 | 106.874 | 106.730 | 106.579 | 106.420 | 106.250 | 106.070 |
| Jan 2003 | 106.495 | 107.955 | 106.457 | 107.961 | 107.837 | 107.709 | 107.577 | 107.440 | 107.297 | 107.147 | 106.989 | 106.823 | 106.646 | 106.459 |
| Feb 2003 | 107.256 | 108.811 | 107.226 | 108.815 | 108.683 | 108.547 | 108.406 | 108.261 | 108.110 | 107.952 | 107.785 | 107.610 | 107.424 | 107.228 |
| Mar 2003 | 107.938 | 109.470 | 107.833 | 109.471 | 109.334 | 109.193 | 109.047 | 108.897 | 108.741 | 108.578 | 108.407 | 108.227 | 108.037 | 107.835 |
| Apr 2003 | 107.682 | 109.204 | 107.611 | 109.205 | 109.073 | 108.936 | 108.796 | 108.650 | 108.498 | 108.339 | 108.172 | 107.997 | 107.810 | 107.613 |
| May 2003 | 107.521 | 109.044 | 107.435 | 109.045 | 108.912 | 108.776 | 108.634 | 108.487 | 108.334 | 108.174 | 108.005 | 107.827 | 107.638 | 107.437 |
| Jun 2003 | 107.617 | 109.180 | 107.513 | 109.181 | 109.043 | 108.901 | 108.754 | 108.601 | 108.442 | 108.276 | 108.102 | 107.917 | 107.722 | 107.515 |
| Jul 2003 | 107.730 | 109.292 | 107.553 | 109.292 | 109.148 | 108.999 | 108.846 | 108.686 | 108.520 | 108.347 | 108.165 | 107.973 | 107.770 | 107.555 |
| Aug 2003 | 108.160 | 109.696 | 107.872 | 109.695 | 109.543 | 109.387 | 109.225 | 109.058 | 108.884 | 108.702 | 108.512 | 108.311 | 108.099 | 107.875 |
| Sep 2003 | 108.478 | 110.035 | 108.163 | 110.036 | 109.879 | 109.718 | 109.551 | 109.379 | 109.200 | 109.013 | 108.818 | 108.612 | 108.394 | 108.165 |
| Oct 2003 | 108.354 | 109.953 | 108.101 | 109.953 | 109.798 | 109.638 | 109.474 | 109.303 | 109.127 | 108.942 | 108.749 | 108.545 | 108.330 | 108.103 |
| Nov 2003 | 107.980 | 109.642 | 107.722 | 109.643 | 109.482 | 109.316 | 109.145 | 108.968 | 108.784 | 108.593 | 108.393 | 108.182 | 107.959 | 107.724 |
| Dec 2003 | 107.821 | 109.515 | 107.530 | 109.516 | 109.348 | 109.177 | 109.000 | 108.816 | 108.626 | 108.429 | 108.221 | 108.004 | 107.774 | 107.533 |
| Jan 2004 | 108.450 | 110.074 | 108.039 | 110.074 | 109.902 | 109.725 | 109.542 | 109.354 | 109.158 | 108.955 | 108.743 | 108.521 | 108.287 | 108.041 |
| Feb 2004 | 109.061 | 110.679 | 108.609 | 110.680 | 110.504 | 110.323 | 110.138 | 109.946 | 109.747 | 109.541 | 109.325 | 109.099 | 108.861 | 108.611 |
| Mar 2004 | 109.695 | 111.385 | 109.276 | 111.386 | 111.206 | 111.022 | 110.832 | 110.636 | 110.434 | 110.223 | 110.004 | 109.774 | 109.532 | 109.279 |
| Apr 2004 | 110.011 | 111.732 | 109.563 | 111.730 | 111.546 | 111.357 | 111.162 | 110.961 | 110.753 | 110.537 | 110.312 | 110.076 | 109.826 | 109.565 |
| May 2004 | 110.560 | 112.355 | 110.053 | 112.355 | 112.156 | 111.953 | 111.745 | 111.531 | 111.309 | 111.080 | 110.841 | 110.592 | 110.329 | 110.056 |
| Jun 2004 | 110.786 | 112.718 | 110.347 | 112.727 | 112.521 | 112.310 | 112.094 | 111.872 | 111.643 | 111.406 | 111.160 | 110.902 | 110.632 | 110.350 |
| Jul 2004 | 110.651 | 112.574 | 110.210 | 112.583 | 112.379 | 112.170 | 111.955 | 111.734 | 111.505 | 111.269 | 111.022 | 110.765 | 110.495 | 110.213 |
| Aug 2004 | 110.706 | 112.605 | 110.221 | 112.615 | 112.409 | 112.198 | 111.981 | 111.758 | 111.528 | 111.289 | 111.040 | 110.781 | 110.508 | 110.224 |
| Sep 2004 | 111.014 | 112.823 | 110.466 | 112.832 | 112.629 | 112.421 | 112.207 | 111.987 | 111.760 | 111.524 | 111.278 | 111.021 | 110.751 | 110.469 |
| Oct 2004 | 111.580 | 113.452 | 110.993 | 113.462 | 113.247 | 113.028 | 112.804 | 112.573 | 112.335 | 112.089 | 111.834 | 111.567 | 111.287 | 110.996 |
| Nov 2004 | 111.577 | 113.514 | 111.008 | 113.514 | 113.296 | 113.073 | 112.844 | 112.610 | 112.368 | 112.118 | 111.859 | 111.589 | 111.306 | 111.011 |
| Dec 2004 | 111.156 | 113.094 | 110.612 | 113.094 | 112.879 | 112.659 | 112.434 | 112.202 | 111.963 | 111.716 | 111.458 | 111.190 | 110.909 | 110.615 |
| Jan 2005 | 111.350 | 113.305 | 110.826 | 113.305 | 113.092 | 112.873 | 112.648 | 112.417 | 112.178 | 111.931 | 111.674 | 111.405 | 111.123 | 110.829 |
| Feb 2005 | 111.925 | 113.966 | 111.421 | 113.966 | 113.745 | 113.520 | 113.289 | 113.052 | 112.806 | 112.553 | 112.289 | 112.014 | 111.725 | 111.425 |
| Mar 2005 | 112.637 | 114.853 | 112.198 | 114.852 | 114.620 | 114.383 | 114.140 | 113.891 | 113.635 | 113.370 | 113.096 | 112.810 | 112.512 | 112.201 |
| Apr 2005 | 113.371 | 115.630 | 112.805 | 115.629 | 115.378 | 115.123 | 114.862 | 114.596 | 114.323 | 114.041 | 113.750 | 113.449 | 113.134 | 112.809 |
| May 2005 | 113.290 | 115.536 | 112.761 | 115.536 | 115.291 | 115.042 | 114.787 | 114.526 | 114.258 | 113.981 | 113.695 | 113.397 | 113.087 | 112.765 |
| Jun 2005 | 113.246 | 115.572 | 112.743 | 115.572 | 115.324 | 115.070 | 114.811 | 114.545 | 114.272 | 113.990 | 113.698 | 113.394 | 113.076 | 112.747 |
| Jul 2005 | 113.684 | 116.088 | 113.051 | 116.087 | 115.817 | 115.542 | 115.262 | 114.975 | 114.681 | 114.378 | 114.066 | 113.742 | 113.404 | 113.055 |
| Aug 2005 | 114.295 | 116.683 | 113.469 | 116.683 | 116.392 | 116.097 | 115.797 | 115.491 | 115.179 | 114.859 | 114.530 | 114.190 | 113.837 | 113.473 |
| Sep 2005 | 115.577 | 118.112 | 114.393 | 118.112 | 117.757 | 117.402 | 117.044 | 116.685 | 116.321 | 115.953 | 115.577 | 115.194 | 114.799 | 114.397 |
| Oct 2005 | 115.748 | 118.373 | 114.700 | 118.373 | 118.026 | 117.678 | 117.327 | 116.973 | 116.614 | 116.250 | 115.878 | 115.497 | 115.105 | 114.704 |
| Nov 2005 | 114.890 | 117.436 | 114.138 | 117.436 | 117.136 | 116.832 | 116.524 | 116.210 | 115.889 | 115.561 | 115.223 | 114.875 | 114.514 | 114.141 |
| Dec 2005 | 114.418 | 116.923 | 113.728 | 116.922 | 116.636 | 116.345 | 116.049 | 115.746 | 115.436 | 115.118 | 114.790 | 114.450 | 114.097 | 113.732 |
| Jan 2006 | 115.208 | 117.821 | 114.480 | 117.814 | 117.513 | 117.208 | 116.897 | 116.581 | 116.257 | 115.924 | 115.582 | 115.229 | 114.862 | 114.484 |
| Feb 2006 | 115.412 | 118.081 | 114.777 | 118.076 | 117.779 | 117.478 | 117.172 | 116.859 | 116.539 | 116.210 | 115.871 | 115.521 | 115.157 | 114.781 |
| Mar 2006 | 116.023 | 118.758 | 115.405 | 118.751 | 118.449 | 118.143 | 117.832 | 117.514 | 117.189 | 116.856 | 116.512 | 116.157 | 115.789 | 115.408 |
| Apr 2006 | 116.945 | 119.723 | 116.142 | 119.723 | 119.395 | 119.063 | 118.726 | 118.384 | 118.036 | 117.679 | 117.313 | 116.937 | 116.547 | 116.147 |
| May 2006 | 117.460 | 120.311 | 116.560 | 120.312 | 119.964 | 119.613 | 119.259 | 118.899 | 118.533 | 118.160 | 117.778 | 117.385 | 116.980 | 116.565 |
| Jun 2006 | 117.731 | 120.571 | 116.777 | 120.570 | 120.220 | 119.866 | 119.508 | 119.144 | 118.774 | 118.397 | 118.010 | 117.613 | 117.202 | 116.782 |
| Jul 2006 | 118.060 | 120.922 | 116.967 | 120.922 | 120.555 | 120.185 | 119.811 | 119.432 | 119.046 | 118.653 | 118.250 | 117.837 | 117.410 | 116.971 |
| Aug 2006 | 118.324 | 121.192 | 117.222 | 121.192 | 120.824 | 120.453 | 120.078 | 119.698 | 119.311 | 118.916 | 118.512 | 118.096 | 117.667 | 117.227 |
| Sep 2006 | 117.815 | 120.586 | 116.947 | 120.585 | 120.255 | 119.920 | 119.579 | 119.233 | 118.879 | 118.516 | 118.143 | 117.759 | 117.361 | 116.951 |
| Oct 2006 | 117.134 | 119.937 | 116.480 | 119.936 | 119.626 | 119.311 | 118.990 | 118.662 | 118.326 | 117.982 | 117.626 | 117.259 | 116.877 | 116.484 |
| Nov 2006 | 116.910 | 119.748 | 116.299 | 119.748 | 119.439 | 119.125 | 118.806 | 118.479 | 118.144 | 117.800 | 117.445 | 117.078 | 116.697 | 116.303 |
| Dec 2006 | 117.016 | 119.928 | 116.383 | 119.927 | 119.609 | 119.286 | 118.956 | 118.620 | 118.276 | 117.922 | 117.558 | 117.181 | 116.790 | 116.387 |
| Jan 2007 | 117.330 | 120.286 | 116.720 | 120.287 | 119.968 | 119.643 | 119.312 | 118.974 | 118.627 | 118.271 | 117.905 | 117.525 | 117.131 | 116.724 |
| Feb 2007 | 117.877 | 120.930 | 117.319 | 120.929 | 120.606 | 120.277 | 119.941 | 119.599 | 119.248 | 118.888 | 118.517 | 118.133 | 117.734 | 117.323 |
| Mar 2007 | 118.913 | 122.031 | 118.245 | 122.030 | 121.688 | 121.341 | 120.987 | 120.627 | 120.259 | 119.881 | 119.493 | 119.092 | 118.677 | 118.250 |
| Apr 2007 | 119.666 | 122.824 | 118.832 | 122.823 | 122.457 | 122.087 | 121.712 | 121.330 | 120.941 | 120.544 | 120.136 | 119.716 | 119.282 | 118.836 |
| May 2007 | 120.292 | 123.574 | 119.318 | 123.573 | 123.177 | 122.777 | 122.373 | 121.964 | 121.549 | 121.125 | 120.692 | 120.248 | 119.791 | 119.323 |
| Jun 2007 | 120.439 | 123.813 | 119.506 | 123.813 | 123.413 | 123.009 | 122.601 | 122.187 | 121.767 | 121.338 | 120.899 | 120.449 | 119.985 | 119.511 |
| Jul 2007 | 120.377 | 123.782 | 119.433 | 123.781 | 123.381 | 122.977 | 122.567 | 122.152 | 121.729 | 121.297 | 120.854 | 120.398 | 119.927 | 119.438 |
| Aug 2007 | 120.288 | 123.555 | 119.354 | 123.554 | 123.170 | 122.781 | 122.387 | 121.985 | 121.575 | 121.157 | 120.727 | 120.285 | 119.828 | 119.358 |
| Sep 2007 | 120.638 | 123.895 | 119.698 | 123.894 | 123.511 | 123.122 | 122.728 | 122.326 | 121.917 | 121.499 | 121.070 | 120.628 | 120.171 | 119.703 |
| Oct 2007 | 120.885 | 124.160 | 119.972 | 124.158 | 123.775 | 123.388 | 122.995 | 122.595 | 122.187 | 121.770 | 121.341 | 120.900 | 120.444 | 119.976 |
| Nov 2007 | 121.481 | 124.898 | 120.448 | 124.897 | 124.485 | 124.069 | 123.647 | 123.220 | 122.786 | 122.342 | 121.889 | 121.424 | 120.944 | 120.453 |
| Dec 2007 | 121.295 | 124.814 | 120.359 | 124.813 | 124.401 | 123.985 | 123.564 | 123.137 | 122.702 | 122.258 | 121.804 | 121.337 | 120.856 | 120.364 |
| Jan 2008 | 121.867 | 125.434 | 120.927 | 125.433 | 125.017 | 124.596 | 124.170 | 123.737 | 123.297 | 122.848 | 122.388 | 121.917 | 121.430 | 120.932 |
| Feb 2008 | 122.250 | 125.799 | 121.280 | 125.798 | 125.380 | 124.958 | 124.531 | 124.098 | 123.656 | 123.206 | 122.746 | 122.273 | 121.785 | 121.286 |
| Mar 2008 | 123.323 | 126.890 | 122.226 | 126.888 | 126.456 | 126.019 | 125.577 | 125.129 | 124.673 | 124.208 | 123.733 | 123.246 | 122.744 | 122.231 |
| Apr 2008 | 124.116 | 127.659 | 122.861 | 127.658 | 127.211 | 126.760 | 126.304 | 125.842 | 125.373 | 124.895 | 124.407 | 123.907 | 123.393 | 122.867 |
| May 2008 | 125.171 | 128.734 | 123.656 | 128.733 | 128.255 | 127.773 | 127.288 | 126.797 | 126.300 | 125.794 | 125.279 | 124.753 | 124.212 | 123.661 |
| Jun 2008 | 126.307 | 130.031 | 124.585 | 130.030 | 129.511 | 128.991 | 128.467 | 127.938 | 127.404 | 126.862 | 126.311 | 125.750 | 125.175 | 124.591 |
| Jul 2008 | 126.918 | 130.714 | 125.114 | 130.712 | 130.179 | 129.644 | 129.104 | 128.561 | 128.011 | 127.454 | 126.888 | 126.311 | 125.721 | 125.120 |
| Aug 2008 | 126.594 | 130.192 | 124.844 | 130.191 | 129.687 | 129.180 | 128.669 | 128.152 | 127.627 | 127.095 | 126.553 | 125.998 | 125.429 | 124.850 |
| Sep 2008 | 126.551 | 130.012 | 124.775 | 130.010 | 129.519 | 129.024 | 128.524 | 128.019 | 127.506 | 126.984 | 126.453 | 125.909 | 125.351 | 124.781 |
| Oct 2008 | 125.500 | 128.699 | 123.794 | 128.698 | 128.243 | 127.784 | 127.319 | 126.847 | 126.368 | 125.879 | 125.379 | 124.867 | 124.339 | 123.799 |
| Nov 2008 | 123.044 | 126.234 | 121.313 | 126.233 | 125.784 | 125.330 | 124.869 | 124.402 | 123.925 | 123.438 | 122.938 | 122.421 | 121.882 | 121.319 |
| Dec 2008 | 121.557 | 124.929 | 119.703 | 124.927 | 124.450 | 123.967 | 123.478 | 122.981 | 122.474 | 121.956 | 121.424 | 120.875 | 120.304 | 119.709 |
| Jan 2009 | 122.095 | 125.472 | 120.272 | 125.471 | 124.996 | 124.516 | 124.029 | 123.534 | 123.030 | 122.514 | 121.985 | 121.439 | 120.871 | 120.278 |
| Feb 2009 | 122.598 | 126.096 | 120.960 | 126.095 | 125.626 | 125.151 | 124.670 | 124.182 | 123.684 | 123.175 | 122.652 | 122.113 | 121.551 | 120.966 |
| Mar 2009 | 122.803 | 126.403 | 121.238 | 126.401 | 125.930 | 125.452 | 124.969 | 124.477 | 123.977 | 123.465 | 122.940 | 122.397 | 121.833 | 121.245 |
| Apr 2009 | 123.053 | 126.718 | 121.560 | 126.716 | 126.245 | 125.768 | 125.285 | 124.794 | 124.294 | 123.783 | 123.259 | 122.717 | 122.154 | 121.566 |
| May 2009 | 123.427 | 127.084 | 121.950 | 127.082 | 126.614 | 126.140 | 125.659 | 125.171 | 124.674 | 124.165 | 123.643 | 123.104 | 122.542 | 121.956 |
| Jun 2009 | 124.485 | 128.176 | 123.010 | 128.174 | 127.704 | 127.228 | 126.745 | 126.254 | 125.754 | 125.243 | 124.717 | 124.174 | 123.608 | 123.016 |
| Jul 2009 | 124.293 | 127.973 | 122.756 | 127.971 | 127.495 | 127.014 | 126.526 | 126.031 | 125.525 | 125.009 | 124.478 | 123.929 | 123.358 | 122.762 |
| Aug 2009 | 124.620 | 128.260 | 122.999 | 128.258 | 127.778 | 127.293 | 126.801 | 126.301 | 125.791 | 125.270 | 124.735 | 124.182 | 123.606 | 123.005 |
| Sep 2009 | 124.706 | 128.340 | 123.064 | 128.338 | 127.857 | 127.370 | 126.877 | 126.375 | 125.864 | 125.342 | 124.805 | 124.250 | 123.673 | 123.070 |
| Oct 2009 | 124.791 | 128.463 | 123.221 | 128.461 | 127.984 | 127.501 | 127.012 | 126.514 | 126.007 | 125.487 | 124.954 | 124.402 | 123.827 | 123.227 |
| Nov 2009 | 124.788 | 128.554 | 123.272 | 128.552 | 128.072 | 127.585 | 127.092 | 126.590 | 126.079 | 125.556 | 125.018 | 124.462 | 123.883 | 123.279 |
| Dec 2009 | 124.544 | 128.328 | 123.008 | 128.326 | 127.842 | 127.353 | 126.856 | 126.351 | 125.836 | 125.308 | 124.767 | 124.207 | 123.623 | 123.015 |
| Jan 2010 | 124.987 | 128.767 | 123.455 | 128.767 | 128.283 | 127.794 | 127.299 | 126.794 | 126.280 | 125.753 | 125.212 | 124.653 | 124.070 | 123.461 |
| Feb 2010 | 124.972 | 128.799 | 123.431 | 128.798 | 128.310 | 127.815 | 127.314 | 126.804 | 126.284 | 125.752 | 125.206 | 124.641 | 124.052 | 123.438 |
| Mar 2010 | 125.442 | 129.327 | 123.979 | 129.327 | 128.841 | 128.348 | 127.849 | 127.341 | 126.823 | 126.293 | 125.748 | 125.185 | 124.598 | 123.986 |
| Apr 2010 | 125.620 | 129.552 | 124.189 | 129.552 | 129.064 | 128.570 | 128.070 | 127.560 | 127.041 | 126.510 | 125.963 | 125.399 | 124.810 | 124.196 |
| May 2010 | 125.678 | 129.653 | 124.263 | 129.650 | 129.160 | 128.664 | 128.161 | 127.649 | 127.128 | 126.594 | 126.045 | 125.478 | 124.887 | 124.270 |
| Jun 2010 | 125.521 | 129.526 | 124.064 | 129.524 | 129.026 | 128.523 | 128.012 | 127.493 | 126.964 | 126.423 | 125.867 | 125.292 | 124.694 | 124.070 |
| Jul 2010 | 125.536 | 129.554 | 124.020 | 129.551 | 129.048 | 128.539 | 128.023 | 127.497 | 126.962 | 126.414 | 125.850 | 125.267 | 124.660 | 124.026 |
| Aug 2010 | 125.756 | 129.732 | 124.168 | 129.730 | 129.224 | 128.712 | 128.192 | 127.664 | 127.126 | 126.574 | 126.008 | 125.422 | 124.811 | 124.174 |
| Sep 2010 | 125.830 | 129.808 | 124.231 | 129.805 | 129.296 | 128.782 | 128.260 | 127.729 | 127.189 | 126.636 | 126.069 | 125.483 | 124.873 | 124.237 |
| Oct 2010 | 125.969 | 129.969 | 124.423 | 129.967 | 129.461 | 128.949 | 128.431 | 127.903 | 127.366 | 126.816 | 126.251 | 125.668 | 125.062 | 124.430 |
| Nov 2010 | 125.920 | 130.024 | 124.459 | 130.022 | 129.514 | 129.001 | 128.481 | 127.951 | 127.412 | 126.860 | 126.294 | 125.709 | 125.100 | 124.466 |
| Dec 2010 | 126.143 | 130.247 | 124.672 | 130.245 | 129.737 | 129.223 | 128.701 | 128.172 | 127.631 | 127.078 | 126.511 | 125.924 | 125.314 | 124.678 |
| Jan 2011 | 126.778 | 130.868 | 125.247 | 130.870 | 130.357 | 129.839 | 129.313 | 128.778 | 128.233 | 127.675 | 127.102 | 126.510 | 125.894 | 125.253 |
| Feb 2011 | 127.363 | 131.513 | 125.857 | 131.510 | 130.995 | 130.473 | 129.945 | 129.407 | 128.859 | 128.298 | 127.722 | 127.127 | 126.508 | 125.864 |
| Mar 2011 | 128.585 | 132.796 | 127.032 | 132.793 | 132.268 | 131.736 | 131.197 | 130.649 | 130.091 | 129.519 | 128.932 | 128.326 | 127.695 | 127.039 |
| Apr 2011 | 129.483 | 133.650 | 127.812 | 133.642 | 133.105 | 132.563 | 132.012 | 131.453 | 130.884 | 130.303 | 129.708 | 129.096 | 128.465 | 127.819 |
| May 2011 | 129.999 | 134.279 | 128.341 | 134.274 | 133.727 | 133.174 | 132.613 | 132.044 | 131.465 | 130.873 | 130.268 | 129.646 | 129.004 | 128.347 |
| Jun 2011 | 129.846 | 134.136 | 128.240 | 134.130 | 133.588 | 133.040 | 132.485 | 131.920 | 131.345 | 130.758 | 130.156 | 129.538 | 128.900 | 128.247 |
| Jul 2011 | 129.983 | 134.255 | 128.327 | 134.252 | 133.707 | 133.156 | 132.597 | 132.029 | 131.451 | 130.860 | 130.255 | 129.633 | 128.991 | 128.334 |
| Aug 2011 | 130.351 | 134.625 | 128.651 | 134.622 | 134.073 | 133.518 | 132.954 | 132.382 | 131.799 | 131.204 | 130.594 | 129.967 | 129.321 | 128.658 |
| Sep 2011 | 130.635 | 134.829 | 128.841 | 134.826 | 134.276 | 133.719 | 133.154 | 132.581 | 131.996 | 131.400 | 130.788 | 130.160 | 129.512 | 128.847 |
| Oct 2011 | 130.373 | 134.551 | 128.599 | 134.549 | 134.002 | 133.449 | 132.888 | 132.318 | 131.738 | 131.144 | 130.536 | 129.911 | 129.266 | 128.605 |
| Nov 2011 | 130.196 | 134.437 | 128.461 | 134.435 | 133.887 | 133.331 | 132.768 | 132.196 | 131.613 | 131.018 | 130.407 | 129.780 | 129.132 | 128.468 |
| Dec 2011 | 129.844 | 134.106 | 128.119 | 134.104 | 133.554 | 132.998 | 132.434 | 131.861 | 131.277 | 130.680 | 130.068 | 129.439 | 128.791 | 128.126 |
| Jan 2012 | 130.438 | 134.696 | 128.631 | 134.706 | 134.147 | 133.581 | 133.008 | 132.426 | 131.833 | 131.227 | 130.607 | 129.969 | 129.312 | 128.638 |
| Feb 2012 | 130.953 | 135.289 | 129.090 | 135.287 | 134.715 | 134.137 | 133.551 | 132.956 | 132.351 | 131.733 | 131.101 | 130.452 | 129.782 | 129.097 |
| Mar 2012 | 131.905 | 136.317 | 129.900 | 136.314 | 135.718 | 135.116 | 134.507 | 133.890 | 133.263 | 132.624 | 131.971 | 131.301 | 130.612 | 129.907 |
| Apr 2012 | 132.284 | 136.728 | 130.239 | 136.726 | 136.122 | 135.513 | 134.897 | 134.272 | 133.638 | 132.992 | 132.331 | 131.654 | 130.958 | 130.247 |
| May 2012 | 132.154 | 136.568 | 130.149 | 136.566 | 135.971 | 135.370 | 134.762 | 134.145 | 133.518 | 132.878 | 132.224 | 131.553 | 130.862 | 130.156 |
| Jun 2012 | 131.956 | 136.368 | 130.067 | 136.366 | 135.785 | 135.198 | 134.602 | 133.998 | 133.383 | 132.755 | 132.112 | 131.452 | 130.771 | 130.074 |
| Jul 2012 | 131.731 | 136.145 | 129.865 | 136.143 | 135.565 | 134.981 | 134.388 | 133.786 | 133.173 | 132.547 | 131.906 | 131.247 | 130.568 | 129.872 |
| Aug 2012 | 132.430 | 136.903 | 130.446 | 136.901 | 136.304 | 135.700 | 135.089 | 134.469 | 133.838 | 133.195 | 132.537 | 131.861 | 131.165 | 130.454 |
| Sep 2012 | 132.988 | 137.514 | 130.939 | 137.512 | 136.901 | 136.285 | 135.661 | 135.029 | 134.386 | 133.731 | 133.061 | 132.375 | 131.668 | 130.946 |
| Oct 2012 | 132.892 | 137.460 | 130.935 | 137.459 | 136.854 | 136.243 | 135.625 | 134.998 | 134.360 | 133.710 | 133.045 | 132.363 | 131.661 | 130.943 |
| Nov 2012 | 132.208 | 136.809 | 130.455 | 136.807 | 136.222 | 135.630 | 135.030 | 134.421 | 133.800 | 133.167 | 132.519 | 131.852 | 131.166 | 130.463 |
| Dec 2012 | 131.770 | 136.441 | 130.143 | 136.439 | 135.860 | 135.275 | 134.681 | 134.078 | 133.463 | 132.835 | 132.192 | 131.531 | 130.849 | 130.151 |
| Source: U.S. Bureau of Labor Statistics. | ||||||||||||||
When the C-CPI-U was introduced in 2002, the Geometric Young formula was selected over the CES formula as a, “plausible, simpler approximate of the Tornqvist in real time.”9 At that time, CES was characterized as a possible alternative. However, many issues related to the substitution elasticity estimate could not be resolved, including a variable estimate of substitution elasticity, an unstable value across months, and a lagged estimate not representative of the current index period.
A variable substitution elasticity estimate would, in principal, be linked to the CPI elementary level of indexes to construct an entire demand system. The CPI elementary structure consists of more than 200 consumption items and 38 geographic areas. This structure would theoretically be based on over 20,000 substitution pairs of items ((211 * 210)/2) in each of the 38 areas. Creating a representative measure of substitution across the requisite elementary cells is not feasible for index estimation; therefore, research shifted to establishing a single “constant” estimate of substitution elasticity.
Robert Cage, John Greenlees, and Patrick Jackman attempted to determine which substitution parameter most consistently produced a CES index that came closest to the final Tornqvist index, based on data from 1987 to 2000. To do this, they calculated monthly CES indexes using the substitution parameter values 0.1, 0.5, and 0.9. Then, the optimal parameter value was selected in which the resulting CES index was closest to the final Tornqvist index. For the original analysis of a constant estimate of substitution elasticity, the stability of the estimator was cited as a major weakness of CES and research showed monthly substitution values that ranged from 0.06 to 2.78.10
Research by John Greenlees in 2010 demonstrated that many of the earlier cited weaknesses could be effectively addressed.11 First, as indicated above, a constant estimate of substitution elasticity could replace a variable estimator. Second, using a model to pool data over longer periods created a more stable estimator by minimizing the impact of monthly price changes. Finally, fixed biennial expenditure shares could be replaced by weights that are updated to an index month comparable to the CPI-U aggregation weights.
Furthermore, Greenlees showed the CES formula could outperform the Geometric Young formula using empirical CPI data, resulting in smaller C-CPI-U revisions and smaller estimates of prediction error. Subsequent research focused on evaluating which preliminary C-CPI-U formula is the best estimate of the final C-CPI-U. The following sections explain why CES formula performed better than the Geometric Young formula for estimation of the preliminary C-CPI-U.
Sigma
Sigma is the measure of elasticity of substitution in the CES formula. To estimate sigma, Greenlees used a regression model developed by Robert Feenstra and Marshall Reinsdorf.12 The model estimates consumer elasticity of substitution as a function of the relationship between the relative change in expenditure shares and the relative change in prices. Greenlees calculated sigma values that ranged from 0.56 to 0.64 and effectively addressed the weakness of an unstable sigma by using the Feenstra–Reinsdorf model and pooling data over annual periods.
The limitations of using a constant elasticity-of-substitution measure for all items and areas remain. The level of consumer substitution between two items such as gasoline and public transportation may be much different from the level of substitution between a different pair, such as coffee and tea. The Feenstra–Reinsdorf pooled regression model, however, measures the average level of consumer substitution across all elementary items and areas to produce a constant sigma value. So the assumption that consumer substitution across all pairs of elementary items is constant remains.
The Feenstra–Reinsdorf model, shown in equation (1), is summarized as the change in expenditures because of a change in price. Sigma is measured as 1 minus the resulting beta (β) of the Feenstra–Reinsdorf pooled regression. The annual expenditure shares are calculated using elementary level annual expenditure weights. The annual average index relatives are calculated using elementary level 12-month average price index relatives.
The Feenstra–Reinsdorf pooled regression over annual periods is expressed as follows:
![]() ,(1)
,(1)
where
is the natural log annual expenditure weight share at the item area stratum level,
is the natural log annual index relative at the item area stratum level,
is the annual reference period of expenditure weights and indexes, and
is the previous annual reference year of expenditure weights and indexes.
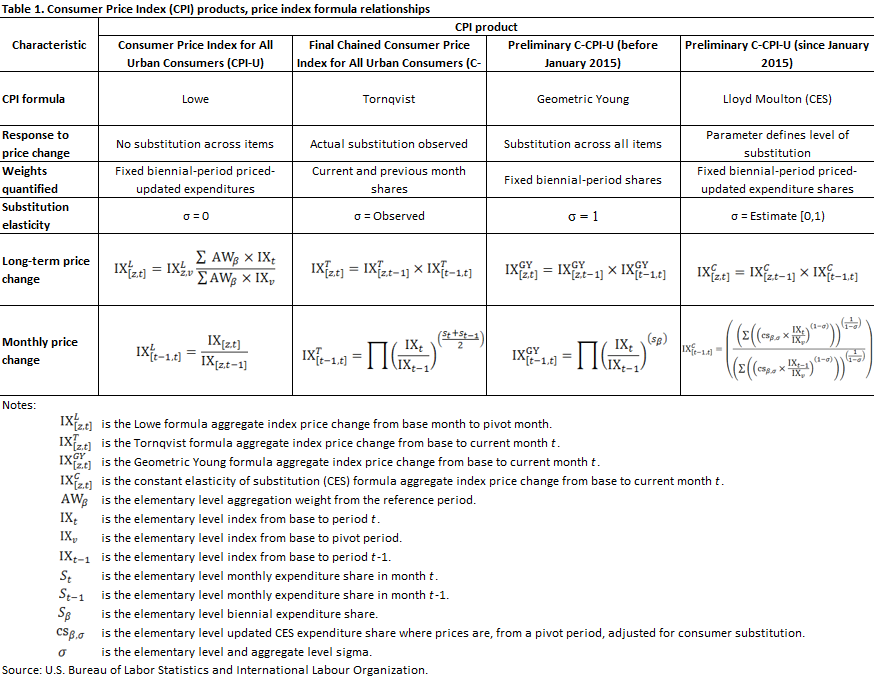
The Feenstra–Reinsdorf formula, equation (1), is weighted as follows:
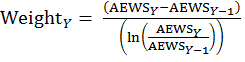 ,(2)
,(2)
where AEWS is the annual expenditure weight share at the item area stratum level.
Greenlees used annual expenditure weight and price index data from 1999 to 2008, and recommended excluding items with large decreasing index relatives. He calculated a relatively stable sigma value that ranged from 0.58 to 0.64, pooled across annual periods.
The results from the Greenlees article are based on an analysis of annual data; however, estimating an optimal sigma using annualized data from biennial expenditure reference periods would procedurally coincide with the weight updates of the CPI-U as demonstrated in equation (3).
The Feenstra–Reinsdorf pooled regression over biennial periods is expressed as follows:
![]() ,(3)
,(3)
where
is the natural log biennial expenditure weight share at the item area stratum level,
is the natural log biennial index relative at the item area stratum level,
is the biennial reference period of expenditure weights and indexes, and
is the previous annual reference year of expenditure weights and indexes.
The above Feenstra–Reinsdorf formula, equation (3), is weighted as follows:
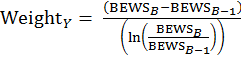 ,(4)
,(4)
where BEWS is the biennial expenditure weight share at the item area stratum level.
Sigma results based on a biennial time frame are summarized in table 2. For the biennial relative years 2003–04:2001–02, the biennial expenditure weight share is equal to the natural log expenditure share and the 24-month average price indexes are based on natural log average price indexes from 2003–04 relative to 2001–02 time frame. The pooled results summarize the Beta values across biennial time periods, and then the sigma pooled is equal to 1 minus beta pooled.
| Biennial period | Relative period | Beta | Pooled biennial periods from 2003-04 | Beta pooled | Sigma pooled | Constant elasticity of substitution index period |
|---|---|---|---|---|---|---|
| 2003–04 | 2001–02 | 0.398 | to 2003–04 | 0.398 | 0.602 | ― |
| 2004–05 | 2003–04 | 0.479 | to 2005–06 | 0.438 | 0.562 | ― |
| 2007–08 | 2005–06 | 0.324 | to 2007–08 | 0.403 | 0.597 | ― |
| 2009–10 | 2007–08 | 0.493 | to 2009–10 | 0.417 | 0.583 | ― |
| 2011–12 | 2009–10 | 0.522 | to 2011–12 | 0.438 | 0.562 | 2014–15 |
| 2013–14 | 2011–12 | 0.229 | to 2013–14 | 0.421 | 0.579 | 2016–17 |
| Source: U.S. Bureau of Labor Statistics. | ||||||
Beta values range from 0.229 to 0.522 over the 6 biennial periods. Beta averaged across the 6 biennial periods is equal to 0.408, comparable to the 2003–04 to 2013–14 beta pooled result of 0.421. Sigma pooled values range from 0.562 to 0.602 across the pooled biennial periods. The CPI has elected to use a sigma value of 0.6, which equals the rounded sigma pooled value for the current period, as well as the previous 5 pooled biennial periods.13
Revisions to the value of sigma will be considered in conjunction with biennial weight revisions, which occur in January of even years. The criteria for making a revision to the sigma value will be based on evaluating the size of changes to the pooled estimate of sigma, and evaluating potential index direction bias. Small changes to sigma have a limited impact on the resulting CES index. Therefore, sigma will only be updated if its optimal value changes by greater than 0.1.
Updated CES weights
The Geometric Young formula uses biennial expenditure weights from 12 to 24 months before the index month. For instance, the initial indexes in 2012 used weights that reflect expenditures made by consumers in 2009 and 2010. The CES formula uses biennial expenditure weights that are more current because the price portion is updated to the current index pivot month by using index relatives, as shown in equation (5). For example, 2009–10 biennial weights are updated by index relatives to represent expenditures in December 2011. Equation (5) displays how the CES expenditure weights are updated to the pivot period. This weight update process is comparable to the last step of aggregation weight calculation. There, elementary level expenditure weights are adjusted by the corresponding elementary level index in order to calculate an expenditure weight value with an implicit price in the pivot month and an implicit quantity of the weight reference period.14
The CES pivoted expenditure weight for biennial reference periods is expressed as follows:
![]() ,(5)
,(5)
where
is the elementary level annualized expenditure weight from the biennial reference period,
is the elementary level 24 month average index from the biennial reference period,
is the sigma for the biennial reference weight period, and
is the elementary level annualized expenditure weight from a biennial reference period in which prices are from a pivot period adjusted for consumer substitution.
CES index relatives
The CPI preliminary estimate of 1-month price change, calculated using the CES formula, is derived from the ratio of CES current and previous month indexes, relative to the pivot month, as shown in equation (6). The pivot-month index is updated every 24 months in conjunction with the biennial weight revisions. The CES functional form also contains the substitution parameters as exponents applied at the elementary-level index relatives, and then at the aggregate level. To create a constant level of substitution across elementary level cells, the same sigma must be applied to the elementary level index relative and the resulting aggregate level index relative.
The CES index for relative biennial periods is expressed as follows:
 (6)
(6)
Distributional analysis of optimal sigma
The following analysis extends the distributional analysis of sigma prepared by Cage, Greenlees, and Jackman by evaluating biennial, annual, and monthly weights to create a real time CES that uses previous period weights. The optimal sigma for each period is the value yielding the closest CES estimate of the final C-CPI-U index. Sigmas ranging from 0 to 1, incremented by 0.01, were tested, as shown in equations (7) and (8). Analysis of the optimal sigma was capped at 1 because in theory, sigma of 1 will result in unitary substitution preferences and therefore will be equal to the Geometric Young formula. CES index relatives are trimmed values in which elementary-level (item/area) relatives greater than 10 are set equal to a value of 10 and relatives less than a value of 0.1 are set equal to a value of 0.1. A histogram of the optimal values is shown in figure 1.
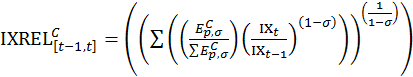 ,(7)
,(7)
![]() (8)
(8)
where
is the weight periodicity (biennial, annual, monthly) from the previous period;
is the sigma for component index period, and aggregate index period ranging from .01 to .99, incremented by .01; and
is the final aggregate index relative.
Optimal sigmas are relatively similar across weight periodicity as shown in figure 2, which displays a count of months with optimal sigmas from 2000–12. The largest difference of absolute values across weight periodicities was 7 months for bins 0.1, 0.3, 0.7, and 0.9. The overall average across weight periods is approximately 0.7, which indicates that the weight periodicity potentially has a minimal impact when optimal sigma is evaluated for this type of analysis.
| Bin | Previous biennial period | Previous year | Previous month |
|---|---|---|---|
| 0.1 | 32 | 27 | 25 |
| 0.2 | 1 | 2 | 3 |
| 0.3 | 11 | 5 | 4 |
| 0.4 | 5 | 4 | 5 |
| 0.5 | 5 | 6 | 3 |
| 0.6 | 3 | 9 | 9 |
| 0.7 | 4 | 11 | 3 |
| 0.8 | 7 | 7 | 11 |
| 0.9 | 4 | 4 | 11 |
| 1.0 | 84 | 81 | 82 |
| Source: U.S. Bureau of Labor Statistics. | |||
Index analysis of optimal sigma
The optimal sigma producing the best CES estimate relative to the final C-CPI-U index varies across index months. The index months can roughly be divided into three optimal sigma periods, as displayed by the periods to the left, center, and right of the gray highlight in figure 3. From January 2000 to December 2003, the optimal sigma is 0.999, indicating unitary substitution preferences. From January 2004 to December 2007, the optimal sigma is 0.8, and from January 2008 to December 2012, the optimal sigma is 0.7.
| Index period | CPI-U | Geometric Young | CES = 0.0 | CES = 0.6 | CES = 0.7 | CES = 0.8 | CES = 0.999 |
|---|---|---|---|---|---|---|---|
| Jan 2000 | 0.005 | 0.081 | 0.003 | 0.046 | 0.054 | 0.063 | 0.081 |
| Feb 2000 | -0.027 | 0.107 | -0.028 | 0.050 | 0.063 | 0.078 | 0.106 |
| Mar 2000 | -0.096 | 0.079 | -0.098 | 0.003 | 0.022 | 0.040 | 0.079 |
| Apr 2000 | -0.153 | 0.028 | -0.155 | -0.051 | -0.032 | -0.013 | 0.028 |
| May 2000 | -0.205 | -0.008 | -0.207 | -0.095 | -0.074 | -0.053 | -0.008 |
| Jun 2000 | -0.342 | -0.017 | -0.343 | -0.158 | -0.125 | -0.090 | -0.017 |
| Jul 2000 | -0.354 | 0.031 | -0.355 | -0.138 | -0.098 | -0.056 | 0.031 |
| Aug 2000 | -0.378 | 0.013 | -0.380 | -0.160 | -0.120 | -0.077 | 0.013 |
| Sep 2000 | -0.429 | -0.018 | -0.431 | -0.198 | -0.156 | -0.112 | -0.018 |
| Oct 2000 | -0.487 | -0.077 | -0.488 | -0.259 | -0.216 | -0.172 | -0.077 |
| Nov 2000 | -0.628 | -0.139 | -0.629 | -0.360 | -0.309 | -0.255 | -0.139 |
| Dec 2000 | -0.760 | -0.239 | -0.762 | -0.476 | -0.422 | -0.364 | -0.239 |
| Jan 2001 | -0.748 | -0.054 | -0.750 | -0.364 | -0.293 | -0.217 | -0.055 |
| Feb 2001 | -0.822 | -0.118 | -0.823 | -0.437 | -0.364 | -0.287 | -0.118 |
| Mar 2001 | -0.842 | -0.170 | -0.843 | -0.479 | -0.409 | -0.335 | -0.171 |
| Apr 2001 | -0.928 | -0.188 | -0.929 | -0.527 | -0.450 | -0.368 | -0.189 |
| May 2001 | -1.015 | -0.174 | -1.016 | -0.558 | -0.470 | -0.377 | -0.175 |
| Jun 2001 | -0.970 | -0.111 | -0.971 | -0.509 | -0.418 | -0.323 | -0.112 |
| Jul 2001 | -0.966 | -0.062 | -0.967 | -0.480 | -0.385 | -0.284 | -0.063 |
| Aug 2001 | -0.896 | 0.027 | -0.897 | -0.404 | -0.307 | -0.204 | 0.026 |
| Sep 2001 | -0.988 | -0.016 | -0.990 | -0.469 | -0.366 | -0.258 | -0.017 |
| Oct 2001 | -0.927 | -0.007 | -0.928 | -0.439 | -0.343 | -0.239 | -0.008 |
| Nov 2001 | -1.028 | -0.014 | -1.030 | -0.487 | -0.381 | -0.267 | -0.016 |
| Dec 2001 | -1.119 | -0.030 | -1.120 | -0.537 | -0.423 | -0.301 | -0.032 |
| Jan 2002 | -1.096 | 0.020 | -1.097 | -0.499 | -0.382 | -0.257 | 0.019 |
| Feb 2002 | -1.167 | -0.005 | -1.168 | -0.545 | -0.423 | -0.293 | -0.007 |
| Mar 2002 | -1.171 | -0.039 | -1.173 | -0.566 | -0.447 | -0.320 | -0.040 |
| Apr 2002 | -1.208 | -0.081 | -1.209 | -0.607 | -0.489 | -0.363 | -0.082 |
| May 2002 | -1.245 | -0.115 | -1.247 | -0.643 | -0.524 | -0.398 | -0.116 |
| Jun 2002 | -1.324 | -0.147 | -1.335 | -0.700 | -0.575 | -0.443 | -0.149 |
| Jul 2002 | -1.286 | -0.043 | -1.291 | -0.621 | -0.490 | -0.352 | -0.045 |
| Aug 2002 | -1.321 | -0.042 | -1.325 | -0.635 | -0.501 | -0.358 | -0.044 |
| Sep 2002 | -1.291 | 0.002 | -1.295 | -0.598 | -0.462 | -0.318 | 0.001 |
| Oct 2002 | -1.345 | -0.033 | -1.347 | -0.641 | -0.503 | -0.357 | -0.034 |
| Nov 2002 | -1.422 | -0.049 | -1.424 | -0.684 | -0.539 | -0.387 | -0.051 |
| Dec 2002 | -1.461 | -0.022 | -1.462 | -0.684 | -0.533 | -0.374 | -0.024 |
| Jan 2003 | -1.460 | 0.039 | -1.466 | -0.652 | -0.494 | -0.328 | 0.037 |
| Feb 2003 | -1.555 | 0.030 | -1.559 | -0.696 | -0.530 | -0.355 | 0.028 |
| Mar 2003 | -1.531 | 0.105 | -1.532 | -0.640 | -0.469 | -0.289 | 0.103 |
| Apr 2003 | -1.522 | 0.071 | -1.523 | -0.657 | -0.491 | -0.315 | 0.069 |
| May 2003 | -1.523 | 0.085 | -1.524 | -0.653 | -0.484 | -0.306 | 0.083 |
| Jun 2003 | -1.563 | 0.104 | -1.564 | -0.659 | -0.485 | -0.301 | 0.102 |
| Jul 2003 | -1.562 | 0.177 | -1.562 | -0.617 | -0.435 | -0.243 | 0.175 |
| Aug 2003 | -1.537 | 0.287 | -1.535 | -0.543 | -0.352 | -0.151 | 0.285 |
| Sep 2003 | -1.557 | 0.315 | -1.558 | -0.536 | -0.340 | -0.134 | 0.312 |
| Oct 2003 | -1.599 | 0.253 | -1.600 | -0.588 | -0.395 | -0.191 | 0.250 |
| Nov 2003 | -1.662 | 0.258 | -1.663 | -0.613 | -0.413 | -0.202 | 0.256 |
| Dec 2003 | -1.694 | 0.290 | -1.695 | -0.608 | -0.401 | -0.183 | 0.288 |
| Jan 2004 | -1.624 | 0.412 | -1.624 | -0.505 | -0.293 | -0.071 | 0.409 |
| Feb 2004 | -1.619 | 0.452 | -1.619 | -0.480 | -0.265 | -0.038 | 0.449 |
| Mar 2004 | -1.690 | 0.419 | -1.691 | -0.529 | -0.309 | -0.079 | 0.416 |
| Apr 2004 | -1.721 | 0.448 | -1.720 | -0.527 | -0.301 | -0.065 | 0.445 |
| May 2004 | -1.795 | 0.507 | -1.795 | -0.520 | -0.282 | -0.032 | 0.504 |
| Jun 2004 | -1.932 | 0.439 | -1.941 | -0.620 | -0.373 | -0.116 | 0.436 |
| Jul 2004 | -1.923 | 0.441 | -1.932 | -0.618 | -0.371 | -0.114 | 0.438 |
| Aug 2004 | -1.899 | 0.485 | -1.909 | -0.583 | -0.335 | -0.075 | 0.482 |
| Sep 2004 | -1.809 | 0.548 | -1.818 | -0.510 | -0.264 | -0.007 | 0.545 |
| Oct 2004 | -1.872 | 0.588 | -1.881 | -0.509 | -0.253 | 0.014 | 0.585 |
| Nov 2004 | -1.936 | 0.569 | -1.937 | -0.541 | -0.282 | -0.012 | 0.566 |
| Dec 2004 | -1.938 | 0.544 | -1.938 | -0.560 | -0.303 | -0.034 | 0.541 |
| Jan 2005 | -1.955 | 0.524 | -1.955 | -0.581 | -0.324 | -0.055 | 0.521 |
| Feb 2005 | -2.040 | 0.504 | -2.040 | -0.627 | -0.364 | -0.088 | 0.501 |
| Mar 2005 | -2.216 | 0.439 | -2.215 | -0.733 | -0.459 | -0.173 | 0.436 |
| Apr 2005 | -2.260 | 0.565 | -2.259 | -0.671 | -0.380 | -0.078 | 0.562 |
| May 2005 | -2.246 | 0.529 | -2.246 | -0.691 | -0.405 | -0.107 | 0.525 |
| Jun 2005 | -2.326 | 0.503 | -2.326 | -0.744 | -0.452 | -0.148 | 0.499 |
| Jul 2005 | -2.404 | 0.632 | -2.404 | -0.695 | -0.382 | -0.058 | 0.629 |
| Aug 2005 | -2.388 | 0.826 | -2.388 | -0.564 | -0.235 | 0.106 | 0.822 |
| Sep 2005 | -2.535 | 1.184 | -2.535 | -0.376 | -0.001 | 0.383 | 1.180 |
| Oct 2005 | -2.626 | 1.048 | -2.625 | -0.502 | -0.130 | 0.251 | 1.044 |
| Nov 2005 | -2.546 | 0.752 | -2.546 | -0.671 | -0.333 | 0.015 | 0.749 |
| Dec 2005 | -2.505 | 0.689 | -2.505 | -0.701 | -0.372 | -0.033 | 0.685 |
| Jan 2006 | -2.613 | 0.728 | -2.605 | -0.716 | -0.374 | -0.021 | 0.724 |
| Feb 2006 | -2.669 | 0.634 | -2.664 | -0.798 | -0.460 | -0.109 | 0.630 |
| Mar 2006 | -2.735 | 0.619 | -2.728 | -0.832 | -0.489 | -0.134 | 0.615 |
| Apr 2006 | -2.778 | 0.802 | -2.778 | -0.734 | -0.368 | 0.008 | 0.798 |
| May 2006 | -2.851 | 0.900 | -2.851 | -0.699 | -0.317 | 0.075 | 0.896 |
| Jun 2006 | -2.840 | 0.953 | -2.840 | -0.666 | -0.279 | 0.118 | 0.949 |
| Jul 2006 | -2.862 | 1.094 | -2.862 | -0.593 | -0.190 | 0.224 | 1.089 |
| Aug 2006 | -2.869 | 1.101 | -2.868 | -0.593 | -0.188 | 0.227 | 1.097 |
| Sep 2006 | -2.770 | 0.869 | -2.770 | -0.701 | -0.328 | 0.057 | 0.865 |
| Oct 2006 | -2.803 | 0.654 | -2.803 | -0.848 | -0.492 | -0.125 | 0.650 |
| Nov 2006 | -2.838 | 0.611 | -2.837 | -0.890 | -0.535 | -0.168 | 0.607 |
| Dec 2006 | -2.912 | 0.633 | -2.912 | -0.907 | -0.543 | -0.166 | 0.628 |
| Jan 2007 | -2.956 | 0.610 | -2.957 | -0.941 | -0.574 | -0.195 | 0.606 |
| Feb 2007 | -3.053 | 0.558 | -3.052 | -1.011 | -0.640 | -0.256 | 0.554 |
| Mar 2007 | -3.118 | 0.668 | -3.117 | -0.968 | -0.580 | -0.179 | 0.663 |
| Apr 2007 | -3.157 | 0.835 | -3.156 | -0.877 | -0.469 | -0.049 | 0.830 |
| May 2007 | -3.281 | 0.974 | -3.281 | -0.833 | -0.400 | 0.044 | 0.970 |
| Jun 2007 | -3.374 | 0.933 | -3.374 | -0.899 | -0.460 | -0.010 | 0.928 |
| Jul 2007 | -3.405 | 0.944 | -3.404 | -0.920 | -0.477 | -0.022 | 0.939 |
| Aug 2007 | -3.267 | 0.934 | -3.266 | -0.869 | -0.439 | 0.003 | 0.930 |
| Sep 2007 | -3.258 | 0.940 | -3.257 | -0.861 | -0.432 | 0.010 | 0.935 |
| Oct 2007 | -3.275 | 0.914 | -3.272 | -0.884 | -0.456 | -0.015 | 0.909 |
| Nov 2007 | -3.417 | 1.033 | -3.416 | -0.861 | -0.408 | 0.057 | 1.028 |
| Dec 2007 | -3.519 | 0.936 | -3.518 | -0.963 | -0.509 | -0.042 | 0.931 |
| Jan 2008 | -3.568 | 0.940 | -3.567 | -0.981 | -0.522 | -0.050 | 0.935 |
| Feb 2008 | -3.549 | 0.970 | -3.547 | -0.956 | -0.495 | -0.022 | 0.965 |
| Mar 2008 | -3.567 | 1.097 | -3.565 | -0.885 | -0.411 | 0.077 | 1.092 |
| Apr 2008 | -3.544 | 1.254 | -3.542 | -0.780 | -0.292 | 0.209 | 1.249 |
| May 2008 | -3.562 | 1.516 | -3.561 | -0.623 | -0.108 | 0.419 | 1.510 |
| Jun 2008 | -3.725 | 1.722 | -3.723 | -0.555 | -0.005 | 0.557 | 1.716 |
| Jul 2008 | -3.796 | 1.804 | -3.794 | -0.536 | 0.030 | 0.607 | 1.798 |
| Aug 2008 | -3.598 | 1.750 | -3.597 | -0.501 | 0.041 | 0.596 | 1.744 |
| Sep 2008 | -3.461 | 1.775 | -3.460 | -0.434 | 0.098 | 0.642 | 1.769 |
| Oct 2008 | -3.199 | 1.706 | -3.198 | -0.379 | 0.121 | 0.633 | 1.701 |
| Nov 2008 | -3.190 | 1.731 | -3.189 | -0.394 | 0.106 | 0.624 | 1.725 |
| Dec 2008 | -3.371 | 1.854 | -3.370 | -0.399 | 0.133 | 0.682 | 1.848 |
| Jan 2009 | -3.377 | 1.823 | -3.375 | -0.419 | 0.110 | 0.657 | 1.817 |
| Feb 2009 | -3.498 | 1.639 | -3.496 | -0.576 | -0.054 | 0.486 | 1.633 |
| Mar 2009 | -3.600 | 1.564 | -3.599 | -0.662 | -0.137 | 0.405 | 1.558 |
| Apr 2009 | -3.665 | 1.493 | -3.664 | -0.731 | -0.206 | 0.335 | 1.486 |
| May 2009 | -3.657 | 1.478 | -3.655 | -0.738 | -0.216 | 0.324 | 1.471 |
| Jun 2009 | -3.691 | 1.475 | -3.689 | -0.758 | -0.232 | 0.311 | 1.468 |
| Jul 2009 | -3.679 | 1.537 | -3.678 | -0.715 | -0.184 | 0.364 | 1.531 |
| Aug 2009 | -3.640 | 1.621 | -3.638 | -0.650 | -0.115 | 0.438 | 1.615 |
| Sep 2009 | -3.634 | 1.642 | -3.632 | -0.636 | -0.099 | 0.456 | 1.636 |
| Oct 2009 | -3.673 | 1.570 | -3.671 | -0.696 | -0.163 | 0.389 | 1.564 |
| Nov 2009 | -3.766 | 1.516 | -3.765 | -0.768 | -0.230 | 0.326 | 1.509 |
| Dec 2009 | -3.784 | 1.536 | -3.782 | -0.764 | -0.222 | 0.337 | 1.530 |
| Jan 2010 | -3.780 | 1.532 | -3.779 | -0.766 | -0.225 | 0.334 | 1.526 |
| Feb 2010 | -3.827 | 1.540 | -3.827 | -0.780 | -0.234 | 0.331 | 1.534 |
| Mar 2010 | -3.885 | 1.463 | -3.885 | -0.851 | -0.306 | 0.257 | 1.456 |
| Apr 2010 | -3.932 | 1.431 | -3.932 | -0.890 | -0.343 | 0.221 | 1.424 |
| May 2010 | -3.975 | 1.414 | -3.973 | -0.916 | -0.367 | 0.200 | 1.408 |
| Jun 2010 | -4.005 | 1.457 | -4.003 | -0.902 | -0.346 | 0.228 | 1.451 |
| Jul 2010 | -4.018 | 1.516 | -4.015 | -0.877 | -0.314 | 0.269 | 1.510 |
| Aug 2010 | -3.976 | 1.588 | -3.974 | -0.818 | -0.252 | 0.334 | 1.582 |
| Sep 2010 | -3.978 | 1.599 | -3.975 | -0.807 | -0.239 | 0.347 | 1.592 |
| Oct 2010 | -4.000 | 1.546 | -3.997 | -0.847 | -0.282 | 0.301 | 1.539 |
| Nov 2010 | -4.104 | 1.461 | -4.101 | -0.940 | -0.374 | 0.212 | 1.455 |
| Dec 2010 | -4.105 | 1.471 | -4.102 | -0.936 | -0.368 | 0.218 | 1.464 |
| Jan 2011 | -4.090 | 1.531 | -4.092 | -0.897 | -0.324 | 0.267 | 1.524 |
| Feb 2011 | -4.150 | 1.506 | -4.147 | -0.935 | -0.359 | 0.236 | 1.499 |
| Mar 2011 | -4.211 | 1.553 | -4.208 | -0.934 | -0.347 | 0.259 | 1.546 |
| Apr 2011 | -4.167 | 1.671 | -4.159 | -0.820 | -0.224 | 0.387 | 1.665 |
| May 2011 | -4.280 | 1.658 | -4.275 | -0.875 | -0.269 | 0.353 | 1.651 |
| Jun 2011 | -4.289 | 1.606 | -4.284 | -0.912 | -0.310 | 0.308 | 1.600 |
| Jul 2011 | -4.272 | 1.656 | -4.269 | -0.878 | -0.273 | 0.350 | 1.649 |
| Aug 2011 | -4.273 | 1.700 | -4.271 | -0.853 | -0.243 | 0.384 | 1.693 |
| Sep 2011 | -4.194 | 1.795 | -4.191 | -0.764 | -0.153 | 0.475 | 1.788 |
| Oct 2011 | -4.178 | 1.774 | -4.176 | -0.771 | -0.163 | 0.462 | 1.768 |
| Nov 2011 | -4.241 | 1.735 | -4.239 | -0.821 | -0.211 | 0.417 | 1.728 |
| Dec 2011 | -4.262 | 1.725 | -4.260 | -0.836 | -0.224 | 0.405 | 1.719 |
| Jan 2012 | -4.259 | 1.807 | -4.268 | -0.790 | -0.169 | 0.468 | 1.800 |
| Feb 2012 | -4.336 | 1.863 | -4.334 | -0.780 | -0.148 | 0.501 | 1.856 |
| Mar 2012 | -4.412 | 2.005 | -4.409 | -0.719 | -0.066 | 0.604 | 1.998 |
| Apr 2012 | -4.444 | 2.045 | -4.442 | -0.708 | -0.047 | 0.630 | 2.037 |
| May 2012 | -4.413 | 2.006 | -4.411 | -0.724 | -0.070 | 0.601 | 1.998 |
| Jun 2012 | -4.412 | 1.888 | -4.410 | -0.799 | -0.156 | 0.504 | 1.881 |
| Jul 2012 | -4.415 | 1.866 | -4.413 | -0.817 | -0.175 | 0.483 | 1.858 |
| Aug 2012 | -4.473 | 1.984 | -4.471 | -0.765 | -0.107 | 0.569 | 1.976 |
| Sep 2012 | -4.526 | 2.050 | -4.523 | -0.743 | -0.073 | 0.614 | 2.042 |
| Oct 2012 | -4.569 | 1.957 | -4.567 | -0.818 | -0.153 | 0.529 | 1.949 |
| Nov 2012 | -4.600 | 1.753 | -4.599 | -0.959 | -0.310 | 0.356 | 1.746 |
| Dec 2012 | -4.671 | 1.627 | -4.669 | -1.065 | -0.422 | 0.239 | 1.619 |
| Source: U.S. Bureau of Labor Statistics. | |||||||
The following analysis compares revision sizes of the final C-CPI-U less the CES and Geometric Young formulas to evaluate how predictive these preliminary formulas are of the final C-CPI-U. This analysis excludes revision chaining to isolate the impact of the preliminary formula.15
For a 1-month change, the revision size of CES is smaller than Geometric Young for 101 out of 156 months (65 percent), as displayed in figure 4. The size of revision associated with each formula is summarized in absolute terms in table 3. For a sum of absolute revision size, CES is 77 percent of Geometric Young. For a mean of absolute errors, CES is 78 percent of Geometric Young. For the root mean squared error revision size, CES is 66 percent of Geometric Young. Each of these measures of revision size of a 1-month change from the CES formula is lower than the Geometric Young formula, indicating the CES formula more closely predicted the final C-CPI-U than the Geometric Young formula.16
| Index period | Geometric Young | Constant elasticity of substitution |
|---|---|---|
| Jan 2000 | 0.000808 | 0.000464 |
| Feb 2000 | 0.000253 | 0.000030 |
| Mar 2000 | -0.000281 | -0.000463 |
| Apr 2000 | -0.000498 | -0.000535 |
| May 2000 | -0.000354 | -0.000430 |
| Jun 2000 | -0.000092 | -0.000621 |
| Jul 2000 | 0.000470 | 0.000205 |
| Aug 2000 | -0.000173 | -0.000223 |
| Sep 2000 | -0.000303 | -0.000363 |
| Oct 2000 | -0.000576 | -0.000583 |
| Nov 2000 | -0.000601 | -0.000982 |
| Dec 2000 | -0.000975 | -0.001135 |
| Jan 2001 | 0.001809 | 0.001113 |
| Feb 2001 | -0.000610 | -0.000689 |
| Mar 2001 | -0.000502 | -0.000397 |
| Apr 2001 | -0.000170 | -0.000443 |
| May 2001 | 0.000145 | -0.000275 |
| Jun 2001 | 0.000601 | 0.000482 |
| Jul 2001 | 0.000463 | 0.000259 |
| Aug 2001 | 0.000855 | 0.000721 |
| Sep 2001 | -0.000410 | -0.000599 |
| Oct 2001 | 0.000084 | 0.000264 |
| Nov 2001 | -0.000072 | -0.000464 |
| Dec 2001 | -0.000153 | -0.000500 |
| Jan 2002 | 0.000485 | 0.000377 |
| Feb 2002 | -0.000244 | -0.000419 |
| Mar 2002 | -0.000318 | -0.000171 |
| Apr 2002 | -0.000401 | -0.000366 |
| May 2002 | -0.000321 | -0.000342 |
| Jun 2002 | -0.000309 | -0.000534 |
| Jul 2002 | 0.000986 | 0.000751 |
| Aug 2002 | 0.000011 | -0.000115 |
| Sep 2002 | 0.000422 | 0.000361 |
| Oct 2002 | -0.000329 | -0.000396 |
| Nov 2002 | -0.000152 | -0.000400 |
| Dec 2002 | 0.000252 | -0.000022 |
| Jan 2003 | 0.000572 | 0.000330 |
| Feb 2003 | -0.000087 | -0.000370 |
| Mar 2003 | 0.000700 | 0.000563 |
| Apr 2003 | -0.000314 | -0.000178 |
| May 2003 | 0.000136 | 0.000033 |
| Jun 2003 | 0.000172 | -0.000054 |
| Jul 2003 | 0.000678 | 0.000395 |
| Aug 2003 | 0.001020 | 0.000712 |
| Sep 2003 | 0.000247 | 0.000080 |
| Oct 2003 | -0.000573 | -0.000490 |
| Nov 2003 | 0.000058 | -0.000246 |
| Dec 2003 | 0.000306 | 0.000040 |
| Jan 2004 | 0.001112 | 0.000980 |
| Feb 2004 | 0.000348 | 0.000255 |
| Mar 2004 | -0.000330 | -0.000417 |
| Apr 2004 | 0.000257 | 0.000029 |
| May 2004 | 0.000520 | 0.000083 |
| Jun 2004 | -0.000630 | -0.000888 |
| Jul 2004 | 0.000029 | 0.000016 |
| Aug 2004 | 0.000394 | 0.000312 |
| Sep 2004 | 0.000562 | 0.000675 |
| Oct 2004 | 0.000331 | 0.000030 |
| Nov 2004 | -0.000167 | -0.000288 |
| Dec 2004 | -0.000210 | -0.000184 |
| Jan 2005 | -0.000190 | -0.000183 |
| Feb 2005 | -0.000203 | -0.000387 |
| Mar 2005 | -0.000608 | -0.000903 |
| Apr 2005 | 0.001099 | 0.000592 |
| May 2005 | -0.000321 | -0.000182 |
| Jun 2005 | -0.000227 | -0.000465 |
| Jul 2005 | 0.001130 | 0.000454 |
| Aug 2005 | 0.001684 | 0.001179 |
| Sep 2005 | 0.003073 | 0.001691 |
| Oct 2005 | -0.001205 | -0.001083 |
| Nov 2005 | -0.002508 | -0.001483 |
| Dec 2005 | -0.000527 | -0.000282 |
| Jan 2006 | 0.000303 | -0.000094 |
| Feb 2006 | -0.000833 | -0.000699 |
| Mar 2006 | -0.000165 | -0.000256 |
| Apr 2006 | 0.001550 | 0.000897 |
| May 2006 | 0.000810 | 0.000323 |
| Jun 2006 | 0.000440 | 0.000296 |
| Jul 2006 | 0.001179 | 0.000635 |
| Aug 2006 | 0.000045 | 0.000013 |
| Sep 2006 | -0.001943 | -0.000931 |
| Oct 2006 | -0.001793 | -0.001275 |
| Nov 2006 | -0.000360 | -0.000369 |
| Dec 2006 | 0.000180 | -0.000139 |
| Jan 2007 | -0.000206 | -0.000272 |
| Feb 2007 | -0.000470 | -0.000553 |
| Mar 2007 | 0.000892 | 0.000437 |
| Apr 2007 | 0.001377 | 0.000809 |
| May 2007 | 0.001136 | 0.000406 |
| Jun 2007 | -0.000357 | -0.000539 |
| Jul 2007 | 0.000098 | -0.000175 |
| Aug 2007 | -0.000076 | 0.000415 |
| Sep 2007 | 0.000022 | 0.000084 |
| Oct 2007 | -0.000232 | -0.000175 |
| Nov 2007 | 0.000954 | 0.000224 |
| Dec 2007 | -0.000789 | -0.000843 |
| Jan 2008 | -0.000007 | -0.000111 |
| Feb 2008 | 0.000224 | 0.000229 |
| Mar 2008 | 0.000978 | 0.000641 |
| Apr 2008 | 0.001228 | 0.000897 |
| May 2008 | 0.002044 | 0.001308 |
| Jun 2008 | 0.001553 | 0.000581 |
| Jul 2008 | 0.000593 | 0.000175 |
| Aug 2008 | -0.000396 | 0.000262 |
| Sep 2008 | 0.000208 | 0.000530 |
| Oct 2008 | -0.000434 | 0.000401 |
| Nov 2008 | 0.000472 | -0.000177 |
| Dec 2008 | 0.001184 | -0.000079 |
| Jan 2009 | -0.000324 | -0.000147 |
| Feb 2009 | -0.001598 | -0.001274 |
| Mar 2009 | -0.000639 | -0.000690 |
| Apr 2009 | -0.000617 | -0.000543 |
| May 2009 | -0.000161 | -0.000040 |
| Jun 2009 | -0.000128 | -0.000108 |
| Jul 2009 | 0.000529 | 0.000330 |
| Aug 2009 | 0.000647 | 0.000533 |
| Sep 2009 | 0.000163 | 0.000121 |
| Oct 2009 | -0.000595 | -0.000480 |
| Nov 2009 | -0.000440 | -0.000570 |
| Dec 2009 | 0.000189 | 0.000018 |
| Jan 2010 | -0.000077 | 0.000005 |
| Feb 2010 | 0.000069 | -0.000112 |
| Mar 2010 | -0.000678 | -0.000539 |
| Apr 2010 | -0.000274 | -0.000296 |
| May 2010 | -0.000138 | -0.000205 |
| Jun 2010 | 0.000358 | 0.000099 |
| Jul 2010 | 0.000477 | 0.000199 |
| Aug 2010 | 0.000560 | 0.000480 |
| Sep 2010 | 0.000078 | 0.000097 |
| Oct 2010 | -0.000442 | -0.000309 |
| Nov 2010 | -0.000676 | -0.000741 |
| Dec 2010 | 0.000058 | 0.000048 |
| Jan 2011 | 0.000422 | 0.000340 |
| Feb 2011 | -0.000256 | -0.000264 |
| Mar 2011 | 0.000257 | 0.000078 |
| Apr 2011 | 0.000846 | 0.000934 |
| May 2011 | -0.000153 | -0.000397 |
| Jun 2011 | -0.000390 | -0.000292 |
| Jul 2011 | 0.000371 | 0.000267 |
| Aug 2011 | 0.000312 | 0.000212 |
| Sep 2011 | 0.000705 | 0.000686 |
| Oct 2011 | -0.000129 | -0.000064 |
| Nov 2011 | -0.000289 | -0.000389 |
| Dec 2011 | -0.000037 | -0.000127 |
| Jan 2012 | 0.000572 | 0.000381 |
| Feb 2012 | 0.000381 | 0.000094 |
| Mar 2012 | 0.000998 | 0.000509 |
| Apr 2012 | 0.000260 | 0.000101 |
| May 2012 | -0.000284 | -0.000125 |
| Jun 2012 | -0.000878 | -0.000578 |
| Jul 2012 | -0.000150 | -0.000140 |
| Aug 2012 | 0.000832 | 0.000422 |
| Sep 2012 | 0.000443 | 0.000193 |
| Oct 2012 | -0.000700 | -0.000569 |
| Nov 2012 | -0.001477 | -0.001082 |
| Dec 2012 | -0.000925 | -0.000823 |
| Source: U.S. Bureau of Labor Statistics. | ||
| Values | Geometric Young formula | Constant elasticity of substitution (CES) formula | CES/Geometric Young |
|---|---|---|---|
| Sum absolute | 8.46 | 6.55 | 77 |
| Mean absolute | 0.055 | 0.043 | 78 |
| Root mean square error absolute | 0.050 | 0.033 | 66 |
| Source: U.S. Bureau of Labor Statistics. | |||
For 12-month change, the revision size of CES is smaller than Geometric Young for 83 out of 132 months (63 percent) as displayed in figure 5. The size of revision is summarized in absolute terms in table 4. For a sum of absolute revision size, CES is 65 percent of Geometric Young. For a mean of absolute revision size, CES is 65 percent of Geometric Young. For the root mean square error of revision size, CES is 57 percent of Geometric Young. Each of these measures of revision size of 12-month change is lower for CES than the Geometric Young formula, indicating the CES formula more closely predicts the final C-CPI-U than the Geometric Young formula.
| Index period | Geometric Young | Constant elasticity of substitution |
|---|---|---|
| Jan 2002 | 0.000724 | -0.001272 |
| Feb 2002 | 0.001090 | -0.001000 |
| Mar 2002 | 0.001281 | -0.000775 |
| Apr 2002 | 0.001052 | -0.000697 |
| May 2002 | 0.000579 | -0.000763 |
| Jun 2002 | -0.000338 | -0.001784 |
| Jul 2002 | 0.000187 | -0.001295 |
| Aug 2002 | -0.000668 | -0.002145 |
| Sep 2002 | 0.000173 | -0.001173 |
| Oct 2002 | -0.000246 | -0.001850 |
| Nov 2002 | -0.000328 | -0.001787 |
| Dec 2002 | 0.000086 | -0.001300 |
| Jan 2003 | 0.000175 | -0.001349 |
| Feb 2003 | 0.000337 | -0.001303 |
| Mar 2003 | 0.001375 | -0.000554 |
| Apr 2003 | 0.001450 | -0.000360 |
| May 2003 | 0.001913 | 0.000021 |
| Jun 2003 | 0.002404 | 0.000510 |
| Jul 2003 | 0.002091 | 0.000148 |
| Aug 2003 | 0.003116 | 0.000988 |
| Sep 2003 | 0.002941 | 0.000703 |
| Oct 2003 | 0.002685 | 0.000604 |
| Nov 2003 | 0.002891 | 0.000758 |
| Dec 2003 | 0.002949 | 0.000822 |
| Jan 2004 | 0.003498 | 0.001480 |
| Feb 2004 | 0.003931 | 0.002108 |
| Mar 2004 | 0.002892 | 0.001119 |
| Apr 2004 | 0.003488 | 0.001336 |
| May 2004 | 0.003902 | 0.001396 |
| Jun 2004 | 0.003085 | 0.000543 |
| Jul 2004 | 0.002414 | 0.000153 |
| Aug 2004 | 0.001770 | -0.000255 |
| Sep 2004 | 0.002090 | 0.000352 |
| Oct 2004 | 0.003030 | 0.000890 |
| Nov 2004 | 0.002809 | 0.000851 |
| Dec 2004 | 0.002271 | 0.000617 |
| Jan 2005 | 0.000933 | -0.000574 |
| Feb 2005 | 0.000370 | -0.001230 |
| Mar 2005 | 0.000087 | -0.001726 |
| Apr 2005 | 0.000948 | -0.001155 |
| May 2005 | 0.000083 | -0.001421 |
| Jun 2005 | 0.000493 | -0.000987 |
| Jul 2005 | 0.001621 | -0.000543 |
| Aug 2005 | 0.002950 | 0.000343 |
| Sep 2005 | 0.005550 | 0.001387 |
| Oct 2005 | 0.003948 | 0.000230 |
| Nov 2005 | 0.001499 | -0.001013 |
| Dec 2005 | 0.001171 | -0.001114 |
| Jan 2006 | 0.001684 | -0.001027 |
| Feb 2006 | 0.001031 | -0.001346 |
| Mar 2006 | 0.001483 | -0.000682 |
| Apr 2006 | 0.001945 | -0.000372 |
| May 2006 | 0.003121 | 0.000150 |
| Jun 2006 | 0.003820 | 0.000940 |
| Jul 2006 | 0.003867 | 0.001127 |
| Aug 2006 | 0.002171 | -0.000077 |
| Sep 2006 | -0.002954 | -0.002738 |
| Oct 2006 | -0.003541 | -0.002922 |
| Nov 2006 | -0.001354 | -0.001792 |
| Dec 2006 | -0.000635 | -0.001654 |
| Jan 2007 | -0.001149 | -0.001828 |
| Feb 2007 | -0.000781 | -0.001683 |
| Mar 2007 | 0.000292 | -0.000982 |
| Apr 2007 | 0.000119 | -0.001069 |
| May 2007 | 0.000451 | -0.000986 |
| Jun 2007 | -0.000364 | -0.001838 |
| Jul 2007 | -0.001463 | -0.002658 |
| Aug 2007 | -0.001581 | -0.002240 |
| Sep 2007 | 0.000427 | -0.001212 |
| Oct 2007 | 0.002049 | -0.000078 |
| Nov 2007 | 0.003422 | 0.000536 |
| Dec 2007 | 0.002411 | -0.000196 |
| Jan 2008 | 0.002620 | -0.000029 |
| Feb 2008 | 0.003331 | 0.000778 |
| Mar 2008 | 0.003420 | 0.000988 |
| Apr 2008 | 0.003266 | 0.001079 |
| May 2008 | 0.004208 | 0.002011 |
| Jun 2008 | 0.006221 | 0.003192 |
| Jul 2008 | 0.006770 | 0.003576 |
| Aug 2008 | 0.006422 | 0.003409 |
| Sep 2008 | 0.006595 | 0.003864 |
| Oct 2008 | 0.006314 | 0.004423 |
| Nov 2008 | 0.005688 | 0.003909 |
| Dec 2008 | 0.007608 | 0.004631 |
| Jan 2009 | 0.007293 | 0.004594 |
| Feb 2009 | 0.005492 | 0.003103 |
| Mar 2009 | 0.003860 | 0.001765 |
| Apr 2009 | 0.002028 | 0.000338 |
| May 2009 | -0.000140 | -0.000984 |
| Jun 2009 | -0.001784 | -0.001657 |
| Jul 2009 | -0.001832 | -0.001493 |
| Aug 2009 | -0.000814 | -0.001235 |
| Sep 2009 | -0.000859 | -0.001641 |
| Oct 2009 | -0.001024 | -0.002537 |
| Nov 2009 | -0.001980 | -0.002983 |
| Dec 2009 | -0.003037 | -0.002914 |
| Jan 2010 | -0.002782 | -0.002757 |
| Feb 2010 | -0.001075 | -0.001565 |
| Mar 2010 | -0.001116 | -0.001413 |
| Apr 2010 | -0.000765 | -0.001160 |
| May 2010 | -0.000740 | -0.001326 |
| Jun 2010 | -0.000243 | -0.001105 |
| Jul 2010 | -0.000297 | -0.001240 |
| Aug 2010 | -0.000384 | -0.001293 |
| Sep 2010 | -0.000470 | -0.001317 |
| Oct 2010 | -0.000315 | -0.001145 |
| Nov 2010 | -0.000553 | -0.001317 |
| Dec 2010 | -0.000689 | -0.001291 |
| Jan 2011 | -0.000185 | -0.000954 |
| Feb 2011 | -0.000517 | -0.001112 |
| Mar 2011 | 0.000433 | -0.000489 |
| Apr 2011 | 0.001582 | 0.000770 |
| May 2011 | 0.001572 | 0.000577 |
| Jun 2011 | 0.000798 | 0.000173 |
| Jul 2011 | 0.000689 | 0.000244 |
| Aug 2011 | 0.000433 | -0.000034 |
| Sep 2011 | 0.001083 | 0.000576 |
| Oct 2011 | 0.001402 | 0.000827 |
| Nov 2011 | 0.001799 | 0.001189 |
| Dec 2011 | 0.001694 | 0.001005 |
| Jan 2012 | 0.001847 | 0.001046 |
| Feb 2012 | 0.002496 | 0.001412 |
| Mar 2012 | 0.003244 | 0.001847 |
| Apr 2012 | 0.002639 | 0.000995 |
| May 2012 | 0.002493 | 0.001265 |
| Jun 2012 | 0.001996 | 0.000973 |
| Jul 2012 | 0.001464 | 0.000557 |
| Aug 2012 | 0.001991 | 0.000770 |
| Sep 2012 | 0.001728 | 0.000271 |
| Oct 2012 | 0.001150 | -0.000243 |
| Nov 2012 | -0.000067 | -0.000952 |
| Dec 2012 | -0.000971 | -0.001661 |
| Source: U.S. Bureau of Labor Statistics. | ||
| Values | Geometric Young formula | Constant elasticity of substitution (CES) formula | CES/Geometric Young |
|---|---|---|---|
| Sum absolute | 26.43 | 17.09 | 65 |
| Mean absolute | 0.200 | 0.129 | 65 |
| Root mean square error absolute | 0.168 | 0.095 | 57 |
| Source: U.S. Bureau of Labor Statistics. | |||
For the 2002 introduction of the C-CPI-U, the CPI opted to implement the Geometric Young formula for the preliminary version. This formula was, in large part, chosen over the CES formula because of problems with the CES formula identified by Cage et al., such as the instability of a monthly sigma. In 2010, Greenlees effectively resolved the instability of sigma with a Feenstra–Reinsdorf regression model that pooled data across biennial periods. The CPI has also identified another improvement in the CES formula: the incorporation of weights updated to a more current pivot period, comparable to the aggregation weights of the CPI-U. This implementation of the CES formula produces a better estimate of the final C-CPI-U than the Geometric Young formula because, for most months, the revisions are smaller and the corresponding absolute revision sizes and root mean square errors are smaller. The updated CES formula allows for a defined level substitution within a biennial time frame that is more flexible than the unitary substitution preferences of the Geometric Young formula, in which substitution across items occurs in response to price change, and more flexible than the substitution preferences of the Lowe formula, in which substitution across items does not occur in response to price change. The CPI implemented the CES formula with the release of the January 2015 CPI-U for the preliminary version of the C-CPI-U. This analysis supports the Greenlees 2010 analysis that the CES formula with a sigma equal to 0.6 approximates the final C-CPI-U better than the Geometric Young formula.
Joshua Klick, "Improving initial estimates of the Chained Consumer Price Index," Monthly Labor Review, U.S. Bureau of Labor Statistics, February 2018, https://doi.org/10.21916/mlr.2018.6
1 See Consumer Price Index: October 2014, USDL-14-2106 (U.S. Bureau of Labor Statistics, November 20, 2014), https://www.bls.gov/news.release/archives/cpi_11202014.pdf.
2 BLS handbook of methods, chapter 17, “The Consumer Price Index” (U.S. Bureau of Labor Statistics, June 2015), p. 2, https://www.bls.gov/opub/hom/pdf/homch17.pdf.
4 Robert Cage, John Greenlees, and Patrick Jackman, “Introducing the chained Consumer Price Index” (paper presented at the Seventh Meeting of the International Working Group on Price Indices, Paris, France, 2003), p. 213, http://www.ottawagroup.org/Ottawa/ottawagroup.nsf/home/Meeting+7/$file/2003+7th+Meeting+-+Cage+&+Greenlees+&+Jackman+-+Introducing+the+Chained+Consumer+Price+Index.pdf.
5 W. E. Diewert, “Exact and superlative index numbers,” Journal of Econometrics 4, 1976, p. 117; Practical guide to producing consumer price indices (International Labour Organization, 2009), p. 3, http://www.ilo.org/public/english/bureau/stat/download/cpi/guide1.pdf.
6 Upper-level estimation uses these price index formulas to aggregate elementary indexes and elementary weights into a final product such as the all-items U.S. city average, the default aggregation level used throughout this article.
7 See P.J. Lloyd, “Substitution effects and bias in nontrue price indexes,” American Economic Review, 1975, vol. 65, issue 3, pp. 301–13; Brent Moulton, “Constant elasticity cost of living index in share relative form,” unpublished manuscript (U.S. Bureau of Labor Statistics, 1996).
8 Consumer price index manual: theory and practice (International Labour Organization, 2004), pg. 6, par. 1.48, http://www.ilo.org/wcmsp5/groups/public/---dgreports/---stat/documents/presentation/wcms_331153.pdf.
9 Cage, et al., “Introducing the chained Consumer Price Index,” p. 228.
10 Ibid.
11 John Greenlees, “Improving preliminary values of the chained CPI-U,” Business and Economic Statistics Section—JSM, 2010, https://www.bls.gov/osmr/research-papers/2010/pdf/st100060.pdf.
12 Robert C. Feenstra and Marshall B. Reinsdorf, “Should exact index numbers have standard errors? Theory and application to Asian growth” (paper presented at the CRIW Conference, September 2003), http://cid.econ.ucdavis.edu/Papers/pdf/Feenstra-Reinsdorf.pdf.
13 Note that this model is sensitive to outlier values, particularly large decreases, because of natural logged index relatives. To mitigate the impact of outliers for the sigma analysis below, index relatives less than 0.25 were set at 0.25. Six cells were trimmed over the 2001–02 to 2013–14 biennial periods: two cells during 2001–02, one cell during 2005–06, and three cells during 2009–10.
14 BLS handbook of methods, chapter 17, p. 33.
15 The published initial C-CPI-U CES formula is revised for 3 quarters in succession by chaining to the terminal month final C-CPI-U. In contrast, the discontinued published C-CPI-U Geometric Young formula is revised annually by chaining to the terminal month final C-CPI-U. For more information, see BLS handbook of methods, chapter 17, p. 34 https://www.bls.gov/opub/hom/pdf/homch17.pdf; BLS News Release, Consumer Price Index- January 2015, p. 5, https://www.bls.gov/news.release/archives/cpi_02262015.pdf.
16 Results support Statistical Canada CPI analysis of price index formulas to reduce substitution bias that results from an asymmetric formula such as Lowe. For more information, see Ning Huang, Waruna Wimalaratne, and Brent Pollard, “Choice of index number formula and the upper-level substitution bias in the Canadian CPI” (paper presented at the 14th Ottawa Group Meeting, May 2015), http://www.stat.go.jp/english/info/meetings/og2015/pdf/t1s4p13_pap.pdf.