An official website of the United States government
 United States Department of Labor
United States Department of Labor

Crossref 0
Analytical Explanation for the Effects of Working from Home on Optimal Environmental Road Pricing, Transportation Research Record: Journal of the Transportation Research Board, 2024.
Automotive dealerships 2019–22: dealer markup increases drive new-vehicle consumer inflation, Monthly Labor Review, 2023.
This article describes U.S. Bureau of Labor Statistics efforts to develop a new set of satellite net inputs to industry price indexes that capture price change for both domestically produced and imported inputs to production. In addition to detailing the methodology for constructing the new indexes, the article discusses their publication structure and potential uses.
In September 2020, the U.S. Bureau of Labor Statistics (BLS) introduced a new set of satellite net inputs to industry price indexes.1 These indexes measure price changes for both domestically produced and imported inputs (excluding capital investment and labor) consumed by most three-digit North American Industry Classification System (NAICS) industry groups.2 The new indexes are calculated by using the detailed price indexes published with the BLS Principal Federal Economic Indicators of the Producer Price Index (PPI) program and the International Price Program (which produces the U.S. Import and Export Price Indexes).
The new satellite series, published on the PPI webpage, is the culmination of a long-term BLS effort to develop a comprehensive set of net inputs to industry price indexes. BLS first proposed calculating such indexes in the late 1970s and published its first series in 1986. The scope of these indexes and the methodology for calculating them were relatively limited, because the indexes were only published for the construction sector of the economy and excluded input prices for services, imports, capital investment, and labor. In 2015, BLS improved the construction industry input indexes by adding prices for services inputs. At the same time, the input price index series was expanded with indexes for a small number of manufacturing and service industries. After 2015, BLS continued its improvement efforts, and, in September 2020, it introduced a new satellite series of input indexes. While the new satellite indexes complement official BLS indexes already in existence, they are produced and published separately from them. The new data series improves upon the existing input price indexes by adding prices for imported goods inputs. In addition, it represents a major coverage expansion, because the official input indexes are only available for construction industries and a limited number of manufacturing and service industries.
This article describes the methodology used to construct the new input indexes, explains their publication structure, and provides examples of their potential uses.
The BLS net inputs to industry price indexes presented in this article measure the average change in prices most domestic industries pay for nearly all inputs to production, excluding capital investment and labor. As noted previously, by tracking price changes for both domestically produced and imported inputs, these new indexes differ from currently published BLS net inputs to industry price indexes, which account only for prices of domestically produced inputs.
To construct an overall net inputs to industry price index, BLS calculates two separate indexes: one measuring price change for domestically produced inputs and the other measuring price change for imported goods inputs.3 The two indexes are then aggregated into an overall input price index that measures price change for industry inputs regardless of their country of origin. PPI commodity indexes are used to construct the domestic portion of the overall index, and import price indexes (MPIs) are used to construct the imported portion of the index.
The first subsection below describes the use of U.S. Bureau of Economic Analysis (BEA) Input–Output
To determine the set of inputs consumed by an industry, BLS relies on the BEA “Use of commodities by industries” table (hereafter referred to as the “use table”).4 The use table provides, on an industry basis, the set and dollar value of products consumed by each domestic industry as inputs to production. The data in the use table are classified by I–O codes, which are very similar to NAICS codes. Importantly, the values included in the use table represent the combined value of domestic and foreign production of the product consumed by an industry. For this reason, the set of domestic inputs included in a given industry input index is the same as the set of imported inputs included in that index. However, as explained below, the weights assigned to the domestically produced commodity differ from those assigned to the imported commodity. The domestic weights reflect the relative value of the input commodity produced in the United States, whereas the imported weights reflect the relative value of the input commodity produced abroad.
The domestic portion of a net inputs to industry price index is constructed from PPI commodity indexes, which measure price change for domestically produced goods, services, and construction products. In determining the appropriate set of PPI commodity indexes to be included in an input price index for an industry, the PPI program matches the industry’s use-table data to PPI codes.5 This matching results in a set of PPIs that correspond with the products the industry consumes.
After the set of PPIs to be included in an industry’s input price index is determined, it is necessary to construct weights for each component PPI. These weights reflect the value of an input relative to all inputs consumed by the industry. The gross weight for a component PPI equals the share of the total value of the commodity consumed by the industry multiplied by the U.S. Census Bureau wherever-made value of shipments for that commodity, which reflects the total value of the commodity’s domestic production in a given year. Assuming there are n industries and m commodities, one can calculate the share of commodity c consumed by industry i in base period b as
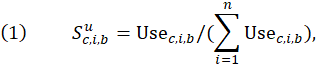
where ![]() denotes the use of commodity c by industry i in base period b; and
denotes the use of commodity c by industry i in base period b; and ![]() is the total use of commodity c by all use-table industries in base period b.
is the total use of commodity c by all use-table industries in base period b.
The gross weight of commodity c in the input index for industry i at time b can then be written as
![]()
where ![]() is the wherever-made value of shipments for commodity c in base period b.
is the wherever-made value of shipments for commodity c in base period b.
After the gross weight of an input commodity is determined, it is converted to a net weight by removing the portion of the commodity’s value that was produced within the industry. Net weighting removes multiple-counting bias from the overall input price index. This bias occurs when prices from several stages of production are included in an aggregate index.
A net weight is calculated by applying a net input ratio to the gross weight. The net input ratio is calculated by using data from the BEA “Make of commodities by industry” table, which provides the set and dollar value of products made by each domestic industry,6 and represents the share of the commodity produced outside the consuming industry. The share of commodity c produced by industry i in base period b is given by
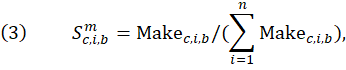
where ![]() is the make of commodity c by industry i in base period b; and
is the make of commodity c by industry i in base period b; and ![]() is the total make of commodity c by all industries in base period b.
is the total make of commodity c by all industries in base period b.
The net input ratio of commodity c for industry i in base period b is the share of commodity c not made by industry i and is calculated as follows:
![]()
The final net value weight for commodity c in the input index for industry i in base period b is calculated as
![]()
which can be rewritten as
![]()
Once the products and weights for a net inputs to industry price index are determined, the index is calculated with a modified Laspeyres formula based on standard PPI methodology.7 An approximation of the PPI aggregate price index for month t is given by
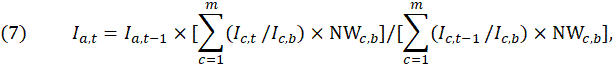
where ![]() is the aggregate price index in period t – 1;
is the aggregate price index in period t – 1; ![]() is the price index for commodity c in period t;
is the price index for commodity c in period t; ![]() is the price index for commodity c in period t – 1;
is the price index for commodity c in period t – 1; ![]() is the price index for commodity c in base period b; and
is the price index for commodity c in base period b; and ![]() is the net weight for commodity c in base period b.
is the net weight for commodity c in base period b.
The imported portion of an input price index is constructed from MPIs, which measure price change for imported commodities and are classified by NAICS codes. As was the case with domestic inputs, determining the set of MPIs to be included in an input price index for an industry requires converting the industry’s use-table data from I–O codes to MPIs (based on NAICS codes). This concordance results in a set of MPIs that correspond with the products consumed by the industry, and these MPIs are the imported components of the input price index for the industry.
After the set of MPIs to be included in an input price index is determined, weights are constructed for the component MPIs. The gross weight for an MPI equals the share of the total value of the commodity consumed by the industry, as shown in equation (1), multiplied by the census import trade value of shipments for the commodity during the base period. This calculation results in weights reflecting only the foreign-produced portion of the input commodity’s value. The gross weight of commodity c in the input index for industry i at time t can then be written as
![]()
where ![]() is the value of imports for commodity c in base period b.
is the value of imports for commodity c in base period b.
Unlike the domestic portion of the input index, the imported portion does not require net weighting. Because domestic industries cannot produce imports, the share of a domestic industry’s production of the import commodity is 0 (![]() ) and the net input ratio is 1. When all net input ratios equal 1, the net weights exactly equal the gross weights.
) and the net input ratio is 1. When all net input ratios equal 1, the net weights exactly equal the gross weights.
Once the products and weights for an inputs to industry price index are determined, the index is calculated with a modified Laspeyres formula, as shown in equation (7).
As noted previously, the domestic and imported input price indexes are aggregated into a total index.8 The aggregate price index at time t is given by
![]()
where![]() is the aggregate price index at time t – 1;
is the aggregate price index at time t – 1; ![]() is the domestic price index for commodity c in period t;
is the domestic price index for commodity c in period t;![]() is the domestic price index for commodity c in period t – 1;
is the domestic price index for commodity c in period t – 1; ![]() is the domestic price index for commodity c in base period b;
is the domestic price index for commodity c in base period b; ![]() is the net weight for domestic commodity c in base period b;
is the net weight for domestic commodity c in base period b; ![]() is the foreign price index for commodity c in period t;
is the foreign price index for commodity c in period t; ![]() is the foreign price index for commodity c in period t – 1;
is the foreign price index for commodity c in period t – 1; ![]() is the foreign price index for commodity c in base period b; and
is the foreign price index for commodity c in base period b; and ![]() is the net weight for foreign commodity c in base period b.
is the net weight for foreign commodity c in base period b.
For each three-digit NAICS industry group, BLS publishes an aggregate input index measuring price change for inputs (excluding capital investment and labor) consumed by the group.9 BLS also publishes separate subaggregate indexes measuring price change for domestically produced and imported inputs consumed by the industry group. Final breakdowns under the domestic subaggregate are published for goods, services, and construction products. No index is produced for industry groups that do not consume a sufficient quantity of inputs in a specific goods or service category. An example of the publication structure is presented in table 1.
| Title | Code |
|---|---|
| Inputs to NAICS 327, nonmetallic mineral product manufacturing, excluding capital investment and labor | IN327 |
| Inputs to NAICS 327, domestically produced products | IN3271 |
| Inputs to NAICS 327, domestically produced goods | IN32711 |
| Inputs to NAICS 327, domestically produced services | IN32712 |
| Inputs to NAICS 327, domestically produced maintenance and repair construction | IN32713 |
| Inputs to NAICS 327, imported goods | IN3272 |
| Note: NAICS = North American Industry Classification System. Source: U.S. Bureau of Labor Statistics. | |
The publication table includes historical index values from the first period of index calculation forward. (In most cases, the index calculation began in December 2018.) Each month, after the release of PPI and MPI data, data for the current period are added to the table, and data for the 4 months prior to the current period are revised. These published data are rounded to the third decimal place.10
This section describes four potential uses for the BLS satellite index series: industry cost analysis, price transmission analysis, contract escalation, and deflation.
The most straightforward use of the net inputs to industry price indexes is to measure changes in industry input costs over time. Calculating the percent change in index levels between two periods provides a measure of the change in an industry’s input costs, excluding those for labor and capital investment. In addition, subaggregate indexes can be used to compare price trends for domestically produced and imported inputs. Finally, subaggregate indexes within the index for domestically produced inputs can be used to compare price trends for domestically produced goods and services inputs.
As an example, figure 1 presents input price indexes for the transportation equipment manufacturing industry group (NAICS 336). From December 2018 through January 2020, the overall input price index rose 0.4 percent, the index for imported inputs fell 1.1 percent, and the index for domestically produced inputs increased 1.0 percent. The inclusion of prices for imported inputs is clearly important for this industry, causing a 0.6-percentage-point difference in the index movements over the sample period. (Without the inclusion, the index rose 1.0 percent.)
| Period | Total | Domestic | Imported |
|---|---|---|---|
| Dec 2018 | 100.000 | 100.000 | 100.000 |
| Jan 2019 | 100.275 | 100.431 | 99.923 |
| Feb 2019 | 100.054 | 100.147 | 99.843 |
| Mar 2019 | 100.418 | 100.737 | 99.697 |
| Apr 2019 | 100.665 | 101.052 | 99.788 |
| May 2019 | 100.634 | 100.983 | 99.842 |
| Jun 2019 | 100.881 | 101.264 | 100.011 |
| Jul 2019 | 100.540 | 100.895 | 99.736 |
| Aug 2019 | 100.699 | 101.107 | 99.776 |
| Sep 2019 | 100.658 | 101.121 | 99.610 |
| Oct 2019 | 100.015 | 100.339 | 99.280 |
| Nov 2019 | 99.920 | 100.262 | 99.144 |
| Dec 2019 | 100.117 | 100.620 | 98.977 |
| Jan 2020 | 100.387 | 101.036 | 98.916 |
| Note: NAICS = North American Industry Classification System. Source: U.S. Bureau of Labor Statistics. | |||
Figure 2 presents the subaggregate price index for domestically produced inputs, along with a further breakdown for domestically produced goods and services. For transportation equipment manufacturing, the input index for domestically produced goods fell 2.9 percent, while that for services rose 6.2 percent. Therefore, the increase in the overall input price index can be traced to prices for domestically produced services, because prices for both imported and domestically produced goods declined. (See figure 1.)
| Period | Total domestic | Domestic goods | Domestic services |
|---|---|---|---|
| Dec 2018 | 100.000 | 100.000 | 100.000 |
| Jan 2019 | 100.431 | 100.248 | 100.669 |
| Feb 2019 | 100.147 | 99.838 | 100.550 |
| Mar 2019 | 100.737 | 99.787 | 101.978 |
| Apr 2019 | 101.052 | 99.458 | 103.136 |
| May 2019 | 100.983 | 99.350 | 103.119 |
| Jun 2019 | 101.264 | 99.074 | 104.129 |
| Jul 2019 | 100.895 | 98.699 | 103.766 |
| Aug 2019 | 101.107 | 98.304 | 104.772 |
| Sep 2019 | 101.121 | 98.125 | 105.038 |
| Oct 2019 | 100.339 | 97.476 | 104.081 |
| Nov 2019 | 100.262 | 97.064 | 104.444 |
| Dec 2019 | 100.620 | 96.839 | 105.565 |
| Jan 2020 | 101.036 | 97.099 | 106.183 |
| Note: NAICS = North American Industry Classification System. Source: U.S. Bureau of Labor Statistics. | |||
This subsection has illustrated that the new input price indexes provide a relatively detailed measure of changes in industry costs, allowing data users to compare price trends for domestically produced and imported inputs and for domestically produced goods and services inputs.
BLS price index data are widely recognized as useful in price adjustment clauses, because they provide an objective price-change measure free from possible manipulation by contracting parties. The satellite series of input price indexes offers a new set of data that contracting parties can use in price adjustment clauses. In some cases, contracting parties may want to make price adjustments based on either broad-level inflation or price change for a specific product. In other instances, the parties may prefer to adjust prices on the basis of changes in overall input costs. For these latter cases, the input price indexes may be useful by providing an objective measure of price change for inputs purchased by specific industry groups.
There are several methods of using BLS data in price adjustment, including the “simple percentage” method, the “adjusting a portion of the base price” method, the “index points” method, the “limits for price adjustment” method, and the “composite indexes” method.11 An example using the composite indexes method, which is often implemented by parties that want to adjust prices on the basis of changes in input costs, is provided below. To implement this method, parties select a set of component price indexes that represent significant inputs and calculate a weighted average of price change for those indexes. The weighted average is then used to adjust the contract price. The composite indexes method often includes prices for goods inputs, services inputs, and labor. The benefit of using a new input index is that it incorporates the near-full set of material and services inputs consumed by an industry group. Without this index, parties would need to identify important material and services inputs individually and then attempt to weight them properly, likely obtaining a less complete input measure than the one calculated by BLS.
Table 2 presents an example of a composite price adjustment for the sale of 500 plastic containers. The contracting parties agree to use the net inputs to industry price index for plastic and rubber products (NAICS 326), to account for price changes in material and services inputs, and the Employment Cost Index, to account for changes in labor input costs.12
| Step | Inputs to NAICS 326 | Employment Cost Index | Composite |
|---|---|---|---|
| 1: Base price (December 2018) = $1,000 per 500 plastic containers | — | — | — |
| 2: 2018 index value | 100.0 | 131.9 | — |
| 3: 2019 index value | 95.4 | 135.8 | — |
| 4: Index relative = (2019 index)/(2018 index) | 0.954 | 1.030 | — |
| 5: Assigned proportion | 0.65 | 0.35 | — |
| 6: (Index relative) × (Assigned proportion) | 0.620 | 0.360 | — |
| 7: Composite relative = Sum [(Index relative) x (Assigned proportion)] | — | — | 0.980 |
| 8: Adjusted price = (Base price) × (Composite relative) | — | — | $980 |
| Note: NAICS = North American Industry Classification System. Source: Authors' calculations based on data from the U.S. Bureau of Labor Statistics. | |||
As shown in row 1 of table 2, in the contract’s base period (December 2018), the price of 500 plastic containers is set at $1,000. To adjust the contract price from the base period to the current period, one begins by deriving relatives of the component indexes, dividing the 2019 index values by the 2018 index values.13 (See row 4.) Then, the index relatives are multiplied by their respective proportions, which have been agreed to by the contracting parties. (See row 6.) The composite relative is then calculated by summing the values from step 6. (See row 7.) Finally, the adjusted price is calculated by multiplying the base period price by the composite relative. (See row 8.) In this example using the composite indexes method, the base-period price of $1,000 is adjusted downward to a new price of $980.
The analysis of price transmission involves estimating the causal relationships between prices in a supply chain. The new satellite net inputs to industry indexes provide data users with an opportunity to analyze price transmission between BLS input and output price indexes for industry groups.
A rigorous price transmission analysis uses econometric time-series models to estimate the causal relationships between prices in a supply chain.14 To be accurately estimated, these econometric models require some minimum amount of data. In the case of the new net inputs to industry price indexes, for which most data begin in December 2018, the sample period is too short for a formal econometric analysis. For this reason, this subsection presents an informal comparison of prices. Figure 3 displays the input and output price indexes for leather and applied product manufacturing (NAICS 316). For comparison purposes, both indexes are rebased to equal 100 in December 2018.
| Period | Input price index | Output price index |
|---|---|---|
| Dec 2018 | 100.000 | 100.000 |
| Jan 2019 | 99.550 | 100.287 |
| Feb 2019 | 99.835 | 100.918 |
| Mar 2019 | 100.263 | 101.033 |
| Apr 2019 | 99.023 | 101.090 |
| May 2019 | 98.674 | 100.746 |
| Jun 2019 | 97.152 | 99.943 |
| Jul 2019 | 97.296 | 100.000 |
| Aug 2019 | 98.055 | 100.402 |
| Sep 2019 | 98.590 | 100.459 |
| Oct 2019 | 97.945 | 100.402 |
| Nov 2019 | 97.850 | 100.459 |
| Dec 2019 | 98.222 | 100.516 |
| Jan 2020 | 98.567 | 100.803 |
| Note: NAICS = North American Industry Classification System. Source: U.S. Bureau of Labor Statistics. | ||
The trends in the input and output price indexes presented in figure 3 are visually similar, suggesting price transmission between the indexes. After an initial drop in the input price index in January 2019, both the input and output price indexes trended upward during the first quarter of 2019, declined for most of the second quarter, and then turned up in July 2019, rising for several months. The trends diverged slightly in October 2019, as the input price index fell while the output price index remained flat. However, for most of the final quarter of 2019, and through January 2020, both indexes trended up. A relatively high correlation of 0.67 between the monthly percent changes in the input and output price indexes also suggests price transmission.
Although the price transmission relationship appears to be relatively strong in leather and applied product manufacturing, it may be weaker in other industries. This is particularly evident in cases in which wages account for a larger share of an industry’s inputs or in which the industry is subject to frequent demand shocks. Figure 4 presents an example for a second industry, accommodation (NAICS 721), in which the relationship between input and output prices appears to be weaker.
| Period | Input price index | Output price index |
|---|---|---|
| Dec 2018 | 100.000 | 100.000 |
| Jan 2019 | 100.453 | 100.184 |
| Feb 2019 | 100.918 | 104.406 |
| Mar 2019 | 101.495 | 106.120 |
| Apr 2019 | 101.842 | 104.223 |
| May 2019 | 102.285 | 106.059 |
| Jun 2019 | 102.471 | 107.222 |
| Jul 2019 | 102.817 | 108.629 |
| Aug 2019 | 102.820 | 108.629 |
| Sep 2019 | 102.817 | 105.202 |
| Oct 2019 | 102.090 | 105.875 |
| Nov 2019 | 102.032 | 103.182 |
| Dec 2019 | 102.191 | 101.469 |
| Jan 2020 | 102.495 | 102.570 |
| Note: NAICS = North American Industry Classification System. Source: U.S. Bureau of Labor Statistics. | ||
While both the input and output price indexes for accommodation saw nearly identical increases over the sample period, they did not exhibit similar turning points, and the output price index displayed much more volatility. The output price index generally rose from December 2018 through the summer of 2019, except for a small downturn in April, and then fell for most of the remainder of 2019 before beginning to increase again in January 2020. In contrast, the input price index rose over almost the entire sample period, except for a small decline from September through November 2019. The substantial difference in trends between the input and output price indexes suggests that price transmission in accommodation is weaker than price transmission in leather and applied product manufacturing. The correlation in monthly percent changes between the input and output price indexes in accommodation is 0.37, which also indicates weak price transmission in that industry.
A closer examination of the output price index for accommodation over a longer period may partially explain the relatively weak price transmission in the industry. Figure 5 presents the output price index for accommodation from January 2012 to December 2019.
| Period | Index level |
|---|---|
| Jan 2012 | 142.4 |
| Feb 2012 | 143.9 |
| Mar 2012 | 149.0 |
| Apr 2012 | 147.6 |
| May 2012 | 146.0 |
| Jun 2012 | 147.2 |
| Jul 2012 | 148.0 |
| Aug 2012 | 148.7 |
| Sep 2012 | 148.4 |
| Oct 2012 | 148.2 |
| Nov 2012 | 144.2 |
| Dec 2012 | 142.1 |
| Jan 2013 | 142.2 |
| Feb 2013 | 145.6 |
| Mar 2013 | 150.7 |
| Apr 2013 | 149.8 |
| May 2013 | 149.2 |
| Jun 2013 | 150.9 |
| Jul 2013 | 154.5 |
| Aug 2013 | 151.5 |
| Sep 2013 | 151.4 |
| Oct 2013 | 150.9 |
| Nov 2013 | 147.9 |
| Dec 2013 | 144.7 |
| Jan 2014 | 147.1 |
| Feb 2014 | 150.4 |
| Mar 2014 | 152.3 |
| Apr 2014 | 152.8 |
| May 2014 | 154.6 |
| Jun 2014 | 155.8 |
| Jul 2014 | 156.8 |
| Aug 2014 | 158.7 |
| Sep 2014 | 156.0 |
| Oct 2014 | 159.0 |
| Nov 2014 | 152.2 |
| Dec 2014 | 149.8 |
| Jan 2015 | 151.1 |
| Feb 2015 | 154.8 |
| Mar 2015 | 158.5 |
| Apr 2015 | 155.9 |
| May 2015 | 156.7 |
| Jun 2015 | 159.6 |
| Jul 2015 | 164.1 |
| Aug 2015 | 161.1 |
| Sep 2015 | 157.8 |
| Oct 2015 | 160.0 |
| Nov 2015 | 152.8 |
| Dec 2015 | 151.2 |
| Jan 2016 | 153.9 |
| Feb 2016 | 156.3 |
| Mar 2016 | 161.4 |
| Apr 2016 | 159.0 |
| May 2016 | 159.3 |
| Jun 2016 | 165.1 |
| Jul 2016 | 167.4 |
| Aug 2016 | 165.6 |
| Sep 2016 | 162.1 |
| Oct 2016 | 162.9 |
| Nov 2016 | 155.5 |
| Dec 2016 | 154.6 |
| Jan 2017 | 155.0 |
| Feb 2017 | 158.2 |
| Mar 2017 | 163.0 |
| Apr 2017 | 163.8 |
| May 2017 | 162.7 |
| Jun 2017 | 166.2 |
| Jul 2017 | 172.8 |
| Aug 2017 | 166.2 |
| Sep 2017 | 163.8 |
| Oct 2017 | 165.0 |
| Nov 2017 | 159.8 |
| Dec 2017 | 157.2 |
| Jan 2018 | 160.2 |
| Feb 2018 | 166.9 |
| Mar 2018 | 172.8 |
| Apr 2018 | 164.5 |
| May 2018 | 165.9 |
| Jun 2018 | 169.2 |
| Jul 2018 | 175.3 |
| Aug 2018 | 173.0 |
| Sep 2018 | 168.3 |
| Oct 2018 | 170.4 |
| Nov 2018 | 164.6 |
| Dec 2018 | 163.4 |
| Jan 2019 | 163.7 |
| Feb 2019 | 170.6 |
| Mar 2019 | 173.4 |
| Apr 2019 | 170.3 |
| May 2019 | 173.3 |
| Jun 2019 | 175.2 |
| Jul 2019 | 177.5 |
| Aug 2019 | 177.5 |
| Sep 2019 | 171.9 |
| Oct 2019 | 173.0 |
| Nov 2019 | 168.6 |
| Dec 2019 | 165.8 |
| Note: NAICS = North American Industry Classification System. Source: U.S. Bureau of Labor Statistics. | |
The output price index for accommodation appears to exhibit a pronounced seasonal pattern, with a strong peak in the summer.15 This seasonal pattern is likely due to an increase in demand for accommodation during the summer months. In contrast, the input index for accommodation does not appear to exhibit this type of seasonality. This difference in seasonal patterns partially explains the relatively weak price transmission between the input and output price indexes. Of course, the long-term trends of the indexes appear to be similar, but the available input price data are insufficient to make this determination.
For industries that consume a substantial amount of imports as inputs, the inclusion of both domestic and imported inputs is likely important for price transmission analysis. To illustrate this point, table 3 presents an example for apparel manufacturing (NAICS 315), showing correlations in 1-month percent index changes (from January 2019 through April 2020) between the industry’s output price index and its input price indexes for total, domestic, and imported inputs.
| Input price index | Relative importance | Correlation with output index |
|---|---|---|
| Total inputs | 100.0 | 0.30 |
| Domestic inputs | 71.1 | 0.22 |
| Imported inputs | 28.9 | 0.24 |
| Note: NAICS = North American Industry Classification System. Source: Authors' calculations based on data from the U.S. Bureau of Labor Statistics | ||
The correlation between the overall input price index (for both domestically produced and imported inputs) and the output price index is approximately 0.08 points (or 36 percent) higher than the correlation between the input index for domestically produced inputs and the output price index. Although this example is based on a short timeframe and a limited analysis method, it illustrates that, in cases in which imports account for a relatively large portion of industry inputs, the inclusion of imported inputs may be important for price transmission analysis.
Deflation entails removing the effect of price changes from a revenue stream in order to separate changes in revenue due to changes in product quantities sold from changes in revenue due to changes in prices. A revenue stream is deflated (i.e., converted from nominal to real) with the following formula:
![]()
Applying equation (10) to a nominal revenue value converts it to a real revenue value expressed in constant dollars from the price index’s base period. In the context of deflation, the base period is the period in which the index equals 100.
For most revenue streams, output price indexes or consumer price indexes that correspond with the industry or product whose revenue is being deflated are used as deflators. For some industries and products, however, corresponding price indexes are not available. BLS may not calculate a price index for an industry or product for two main reasons. First, the product or industry may be in scope for a BLS pricing program, but the program may lack the resources to produce the price index. For example, PPI does not currently publish price indexes for industries in the education sector (NAICS 611) and for the custom computer programming services industry (NAICS 541511). Second, the product or industry may be out of scope for BLS because it has no marketed output. For example, the temporary shelters industry (NAICS 624221), which provides short-term emergency shelter for victims of violence and child abuse, as well as for other people in need, does not typically sell its output. Therefore, BLS cannot calculate an output price index for temporary shelters, because there are no prices for that industry’s output. In cases in which no output or consumer price index is available, an input index can be used as a deflator.
Table 4 presents an example of deflating U.S. Census Bureau revenue data for the social assistance industry group (NAICS 624) with the BLS input price index for that group. BLS does not currently publish an output price index for social assistance, because most industries within this three-digit NAICS group are out of scope for the PPI program. In the example presented in table 4, the net inputs to industry price index is first converted from a monthly index to a quarterly index by averaging the three monthly price indexes in each quarter. This step is necessary because the census revenue data are only available quarterly. Next, the quarterly price index data are rebased to equal 100 in the first quarter of 2019. This step ensures that, after the deflation is complete, the resulting revenue will be expressed in constant first-quarter-2019 dollar values. The nominal revenue (shown in the third data column of table 4) is then converted to real revenue with the use of equation (10).
| Quarter | Price index | Price index rebased | Nominal revenue (millions of dollars) | Real revenue (millions of dollars) |
|---|---|---|---|---|
| First quarter | 100.418 | 100.000 | $49,431 | $49,431 |
| Second quarter | 102.145 | 101.720 | 51,385 | 50,516 |
| Third quarter | 102.423 | 101.997 | 51,194 | 50,192 |
| Fourth quarter | 102.346 | 101.920 | 55,954 | 54,900 |
| Note: NAICS = North American Industry Classification System. Source: Authors' calculations based on data from the U.S. Bureau of Labor Statistics and the U.S. Census Bureau. | ||||
Finally, it should be noted that the example presented in table 4 is likely oversimplified. In practice, data users performing a deflation for social assistance may want to combine BLS input price index data with wage data, because wages represent a substantial portion of this industry group’s inputs.16
In September 2020, BLS introduced a new set of satellite net inputs to industry price indexes. These indexes measure price change for inputs (excluding capital investment and labor) consumed by most three-digit NAICS industries and are constructed by combining PPI commodity indexes and MPIs. This article has identified a number of potential uses for the new indexes, including industry cost analysis, contract escalation, price transmission analysis, and deflation. BLS will be further examining this satellite data series and soliciting user feedback on it, aiming to make it an official series in the future.
Jayson Pollock, and Jonathan C. Weinhagen, "A new BLS satellite series of net inputs to industry price indexes: methodology and uses," Monthly Labor Review, U.S. Bureau of Labor Statistics, September 2020, https://doi.org/10.21916/mlr.2020.22
1 As of this article’s release, the term “satellite” is used to describe the new input price indexes because, while the indexes provide data that expand the analytical utility of the currently published input price indexes, they are not considered an official U.S. Bureau of Labor Statistics (BLS) output. Upon further review, BLS may release the new index series as an official output as early as 2021.
2 Input components for which BLS does not calculate price indexes are also excluded from the satellite series. Most importantly, BLS does not calculate price indexes for approximately 28 percent of domestically produced services or any imported services. For cases in which coverage is missing for a substantial portion of an industry’s inputs, a net input price index for that industry is not produced.
3 BLS does not publish an overall services import price index; imported services account for one-fifth of U.S. imports. Import price index measures are available at https://www.bls.gov/mxp/.
4 The BEA use table is available at http://www.bea.gov/industry/io_annual.htm.
5 The industry input index excludes cases in which the I–O code is out of scope or not currently covered by the PPI program. BLS also implements a cutoff rule that removes commodities accounting for less than 0.5 percent of an industry’s total inputs from the industry’s input indexes. The cutoff rule substantially reduces the work required to build and maintain the net inputs to industry price indexes, while having a negligible effect on index movements.
6 The BEA “Make of commodities by industries” table is available at http://www.bea.gov/industry/io_annual.htm.
7 For an overview of the PPI methodology, see chapter 14, “Producer prices,” Handbook of Methods (U.S. Bureau of Labor Statistics), https://www.bls.gov/opub/hom/pdf/homch14.pdf.
8 See ibid.
9 The BLS satellite net inputs to industry price indexes for three-digit NAICS industry groups are published at https://www.bls.gov/ppi/input-indexes/. Input indexes were not calculated if prices for a substantial portion of an industry group’s inputs were not available.
10 Official PPIs are revised only once, 4 months after original publication. In addition, official PPI data are rounded to the first decimal place.
11 For descriptions of these methods and for an overview of applying PPIs to price adjustment (escalation) clauses, see “Price adjustment guide for contracting parties,” Producer Price Indexes (U.S. Bureau of Labor Statistics), https://www.bls.gov/ppi/publications/price-adjustment-guide-for-contracting-parties.htm.
12 The specific Employment Cost Index (ECI) used in the example is for total compensation (wages and benefits), private industry, and goods-producing industries (database code CIU201G000000000I, https://www.bls.gov/ncs/ect/). BLS does not directly assist in writing contracts and does not make recommendations about what data or indexes contracting parties should use.
13 Because the ECI is published on a quarterly basis, fourth-quarter values are used for the price adjustment calculation. The input index is a monthly index, so December values are used for the calculation.
14 See, for example, Jonathan C. Weinhagen, “Price transmission: from crude petroleum to plastics products,” Monthly Labor Review, December 2006, https://www.bls.gov/opub/mlr/2006/12/art4full.pdf.
15 Formal seasonality testing based on the U.S. Census Bureau X-12-ARIMA program indicates that this series exhibits statistically significant seasonality.
16 The BLS ECI series is a potential source of data for measuring wages. These data can be found at https://www.bls.gov/ncs/ect/.