An official website of the United States government
 United States Department of Labor
United States Department of Labor

Crossref 0
Income inequality and healthcare utilization of the older adults-based on a study in three provinces and six cities in China, Frontiers in Public Health, 2024.
The Modeled Wage Estimates (MWE) program publishes mean hourly wages by occupation, geographic area, and worker characteristic (for example, full-time workers). The MWE program combines data from two U.S. Bureau of Labor Statistics programs: the Occupational Employment Statistics (OES) and the National Compensation Survey (NCS). For the first few years of the MWE program, there were no estimates of variance. In 2018, variance estimates were published for the first time for the MWE program, for the May 2017 reference month. This article first shows how the OES and NCS microdata are combined to produce a mean wage estimate. It then focuses on the new variance estimation methodology, highlighting how the variability of both the OES and NCS sample designs are simultaneously captured. A small sample of MWE mean wages and variances are provided for the most recent estimates, for the May 2018 reference month.
The Occupational Employment Statistics (OES) and the National Compensation Survey (NCS) programs both estimate mean hourly wages. Their data come from two independent establishment samples spanning the nation. The OES program collects employment and wage data from all occupations in an establishment, whereas the NCS program only collects data from a sample of occupations. The NCS program also collects information on worker characteristics, such as full- or part-time status, union or nonunion status, whether pay is time based only (for example, a wage) or contains incentive-based pay (for example, commissions), and the NCS generic work level.1 The OES program does not collect data on these worker characteristics.
The OES program samples about 1.2 million establishments over a 3-year period. The NCS program samples only about 8,000 establishments. The OES program produces reliable estimates for many estimation domains, such as occupations within geographic areas. The OES program does not have worker-characteristic breakouts. The NCS program, however, can produce worker-characteristic breakouts. But for many small domains, the NCS sample size is too small to produce reliable estimates, either for the entire domain or for some of its worker-characteristic breakouts.
The Modeled Wage Estimates (MWE) program was created to bridge this coverage gap between the OES and NCS programs. The MWE program produces worker-characteristic estimates for many OES estimation domains, including small OES domains in which NCS estimates are unreliable. The MWE program combines microdata from both the OES and NCS programs. The MWE estimation methodology was previously introduced in a 2013 Monthly Labor Review article, “Wage estimates by job characteristic: NCS and OES program data.”2 As will be shown, the mean wage estimator for the MWE program is identical to the mean wage estimator for the OES program, except for the inclusion of a new factor, the characteristic proportion for the worker characteristic. The proportion is an estimate of the fraction of workers (in an OES microdata row) who have a worker characteristic—for example, the fraction that is full time or the fraction that is both part time and in NCS generic work level 9. The MWE program has breakouts for 54 worker characteristics. See appendix A for a list.
To gauge the reliability of any estimator, we estimate its variance. The variance is the mean squared deviation of the sample estimates from the mean of the sample estimates, evaluated over the entire sampling distribution. The variance measures the dispersion of the sampling distribution. High variance indicates high dispersion, and low variance means that the estimates are tightly clustered. The lower the variance, the more likely that a randomly selected sample estimate from this distribution will be close to its mean and, hence, the more reliable the sample design. The variance also can be used to estimate a confidence interval (margin of error).
For any estimator, its variance cannot be calculated directly because we have only one sample, so its variance is estimated. We can estimate this variance in several ways. One method is the Taylor series, which is used to estimate one component of the variance of the OES mean wage estimator.3 Another method is Fay’s method of balanced repeated replication (Fay’s BRR), which is used by the NCS program.4 After weighing the options for the MWE program, we decided to use Fay’s BRR.
To compute the Fay’s BRR variance estimate for the MWE program, we start with the original mean wage estimate for the MWE program, which we call the full-sample estimate. Then we compute R new mean wage estimates, called replicate estimates. Each replicate estimate is computed with the use of the same formula as the full-sample estimate, except that the sampling weights are perturbed. The sampling weight of each noncertainty sampled unit is either increased by 50 percent or decreased by 50 percent. The choice of whether to increase or decrease is not static; rather, it will vary both by sample unit and replicate. The Fay’s BRR variance estimate is 4 times the mean squared deviation of these R replicate estimates from the full-sample estimate. Multiplying the mean squared deviation by four is necessary to properly scale the result.
The perturbation patterns for the replicates are designed to capture how the actual sample units and weights might vary from sample to sample. To define these perturbation patterns, we first divide the microdata into special subsets called variance strata, which are based on first-stage sampling strata. A sampling stratum is a subset of the sampling frame from which independent samples are selected. Ideally, the variance strata should be these first-stage sampling strata. But in some cases, we collapse the variance strata together. In other cases, we split them up.
Once formed, each variance stratum is then randomly split into two subsets, labeled “variance PSU 1” and “variance PSU 2” (PSU = primary sampling unit). For each replicate and stratum pair, we upweight one variance PSU and downweight the other variance PSU. That is, we first select one of the two variance PSUs. If a noncertainty unit is in this selected variance PSU, we increase its weight by 50 percent; otherwise, we decrease its weight by 50 percent. The pattern of perturbations, across all replicates and strata, are carefully chosen to ensure a good balance.
Adapting Fay’s BRR to the MWE program is challenging because the MWE variance estimator must capture the sampling variance of both the NCS and OES sample designs. Hence, we use a mixture of variance strata. Some MWE variance strata are based on the NCS locality sample design, some on the NCS national sample design, and the rest on the OES sample design. Each MWE estimation domain has a unique set of MWE variance strata. This practice of defining new variance strata for each MWE domain deviates from the method used for other NCS products, in which only one set of variance strata is used for all NCS domains.
The OES sample has about 1.2 million establishments spread over six semiannual OES sampling panels. Each establishment is contacted only once. From most establishments, the OES program collects the employment of each “estab-occ-interval,” which is a wage interval within a six-digit Standard Occupational Classification (SOC) code occupation within the establishment. From some establishments, however, the OES program collects the individual wage rate of each worker. A wage interval is a range of mean hourly wages, for example $7.25 to $9.25 per hour. There are 12 OES wage intervals, which can vary by panel, and up to 840 possible SOC codes.5
The OES program computes mean hourly wage estimates for the nation, the states, and OES localities. For May 2018 estimates, there were two types of OES localities: metropolitan statistical areas (MSAs) and balance of state (BOS) areas. A BOS area is a cluster of nonmetropolitan counties. Each MSA can overlap more than one state, yet each BOS area is contained in a single state.
The NCS sample has about 8,000 establishments spread over several annual sampling panels. Each establishment in each sampling panel is recontacted every quarter, and its data are updated, until the sampling panel rotates out. From each establishment, the NCS program selects a sample of job quotes. Each sampled quote is a collection of workers who share the same six-digit SOC code and the same set of worker characteristics, such as full- or part-time status, union or nonunion status, time or incentive status, and NCS work level. From each quote, the NCS program collects the hourly wage rate of each worker. The NCS program also collects information on benefits, such as benefit costs, access, and participation. These microdata support the Employment Cost Index (ECI), the Employer Costs for Employee Compensation (ECEC), the Employee Benefits publications, and other statistics.6 The occupational and geographic scope of the NCS target population is similar to the scope of the OES target population. However, the NCS sampling strata are too coarse to support estimates for most OES localities, and they cannot support any state estimates.
For the May 2018 reference month, mean wage estimates for the MWE program are computed for 521 OES localities. In contrast, the NCS program has only 120 national sampling strata made of 24 NCS sample areas split into 5 aggregate industry groups. These 24 NCS sample areas are the 15 largest NCS localities and 9 broad “rest-of-census-division” areas. To form a rest-of-census-division area, we start with the entire division and remove all territory that overlaps any of the 15 largest NCS localities. Hence, the NCS program can only support the MWE localities that correspond to the 15 largest NCS sample areas. In addition, the NCS program has too few sample units to produce reliable mean wage estimates for the MWE program for most MWE geographic and occupational domains, let alone for worker-characteristic breakouts of these domains. On the other hand, although the OES program has adequate occupational and geographic coverage, the OES program cannot produce any breakouts by worker characteristic.
The MWE program is designed to bridge these coverage gaps. The mean wage estimates of the MWE program are anchored on the broad and deep occupational and geographic coverage of the OES microdata. These OES microdata are then supplemented with information on worker characteristics only found in NCS microdata. The OES microdata are used as a skeleton, to allow reliable estimates for some small OES domains. The NCS microdata are used to estimate mean wages for each worker characteristic for each OES domain. For each OES estab-occ-interval and for each worker characteristic, ideally we would like to know the true characteristic proportion, which is the fraction of workers in the OES estab-occ-interval who have the given characteristic. But the OES does not collect data on worker characteristics, so the true characteristic proportion is unknown and hence must be imputed.
The NCS microdata are used to impute these characteristic proportions. First, we partition the NCS microdata into imputation cells. In order for us to compute reliable estimates of characteristic proportions, each cell should have a sufficient amount of NCS microdata. Cells with insufficient microdata are collapsed together with other cells until each collapsed cell has enough microdata. The resulting collapsed cells are called final imputation cells. Next, using just the NCS microdata in the final imputation cell, we compute an NCS characteristic proportion for each final imputation cell and each of the 54 worker characteristics. Lastly, we map each OES estab-occ-interval to one final imputation cell. The 54 imputed characteristic proportions for this OES estab-occ-interval are set equal to the corresponding 54 characteristic proportions for the NCS final imputation cell to which the OES estab-occ-interval maps.
Within a single OES domain, however, this mapping will be imperfect. Because of the smaller NCS sample size, many of these final imputation cells may not be subsets of the OES domain. As a result, the imputed characteristic proportions used for an OES domain will often be based in part on NCS microdata outside the OES domain. For example, the OES domain might be restricted to one locality, such as Lexington, Kentucky. However, the associated NCS imputation cell might span all of the East South Central census division (Alabama, Kentucky, Mississippi, and Tennessee). In another example, the initial imputation cell is restricted to a single six-digit SOC code, yet the final cell, after collapsing, spans an entire major occupational group (MOG).
The mean wage estimator for the MWE program is nearly identical to the mean wage estimator for the OES program, so discussing the OES mean wage estimator first is helpful. An OES estimation domain D is an occupational or industry domain within a geographic domain. The OES mean hourly wage for D is given by
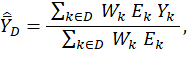
where ![]() = OES estimate of the mean hourly wage for domain D; for OES interval data, k = OES estab-occ-interval and Yk = NCS interval-mean wage that is associated with k; for OES point data, k = OES individual wage record in an OES estab-occ and Yk = OES individual wage rate for k; and for the other variables, D = OES estimation domain (which is an occupational or industry domain in a geographic domain), Wk = OES weight for the OES establishment containing k, and Ek = OES employment of k.
= OES estimate of the mean hourly wage for domain D; for OES interval data, k = OES estab-occ-interval and Yk = NCS interval-mean wage that is associated with k; for OES point data, k = OES individual wage record in an OES estab-occ and Yk = OES individual wage rate for k; and for the other variables, D = OES estimation domain (which is an occupational or industry domain in a geographic domain), Wk = OES weight for the OES establishment containing k, and Ek = OES employment of k.
If k is an estab-occ-interval, the NCS interval mean wage Yk is computed as follows. First, we collect 3 years of NCS microdata (using the June quarter). We then create six NCS datasets, one for each OES panel. For the first year, NCS data are duplicated to create panels 5 and 4, the second year creates panels 3 and 2, and the third year creates panels 1 and 0. Next, if a wage is below the federal minimum wage, it is increased to this minimum, and some upper outlier wages are dropped. We then assign each row of NCS data to an OES wage interval, using the interval definitions for that panel. Finally, the NCS data are divided into interval-mean estimation cells, on the basis of panel and interval number. The estab-occ-interval k is mapped to one of these cells Mk, and an initial mean wage is computed for the cell as
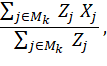
where j = individual wage record in an NCS quote; Mk = interval-mean cell, associated with k; Zj = NCS individual weight for j; and Xj = NCS mean hourly wage for j.
The interval means for the five older OES panels are then aged forward with the use of the ECI. That is, if the ECI went up by 2 percent, the interval means are increased by 2 percent. The aging factors vary by panel and MOG. One final adjustment may be required, since for some OES panels and states, the state minimum wage exceeds the lower bound of interval 1 or even interval 2. In these situations, the interval mean wages are shifted up. In some cases, the value is replaced with the geometric mean of the endpoints of a wage interval.
The estimation domains for the MWE program are occupational domains within geographic domains. Most of the occupational domains are six-digit or two-digit SOC codes. The rest are small clusters of six-digit SOC codes, called rollup SOC codes. The geographic domains for May 2018 estimates include 521 OES localities, 51 states (when we include the District of Columbia), and the nation. Currently, we compute mean hourly wages for the MWE program for four dimensions of worker characteristics: union or nonunion, full or part-time, time or incentive, and work levels (levels 1–15, plus an extra category for nonleveled quotes). These definitions yield 22 worker characteristics. We also break out the full-time and part-time estimates by work level, which adds 32 more worker characteristics. Hence, each MWE estimation domain has 54 NCS worker characteristics. See appendix A for a list.
The mean wage estimator for the MWE program is nearly identical to the mean wage estimator for the OES program, except for the introduction of a new factor, the characteristic proportion FkC. For the MWE program, the mean hourly wage for a domain D and worker characteristic C is given by
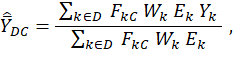
where ![]() = estimate of the mean hourly wage for the MWE program for domain D and worker characteristic C; the symbol D = MWE estimation domain (which is an occupational domain in a geographic domain); C = worker characteristic (full time, union, time-based-pay, work level, etc.); the subscript k and the variables Wk, Ek, and Yk are the same as in the OES mean wage estimator shown previously; and FkC = MWE characteristic proportion for C, that is associated with k. Note that the definition of D has changed compared with what is used in the OES program. For the OES program, a domain is an occupational or industry domain in a geographic domain. For the MWE program, however, currently no mean wage estimates exist for industry groups (for any geographic breakout).
= estimate of the mean hourly wage for the MWE program for domain D and worker characteristic C; the symbol D = MWE estimation domain (which is an occupational domain in a geographic domain); C = worker characteristic (full time, union, time-based-pay, work level, etc.); the subscript k and the variables Wk, Ek, and Yk are the same as in the OES mean wage estimator shown previously; and FkC = MWE characteristic proportion for C, that is associated with k. Note that the definition of D has changed compared with what is used in the OES program. For the OES program, a domain is an occupational or industry domain in a geographic domain. For the MWE program, however, currently no mean wage estimates exist for industry groups (for any geographic breakout).
The characteristic proportion for k and C is computed from NCS microdata as
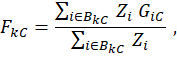
where i = individual wage record in an NCS quote, BkC = characteristic-proportion final imputation cell associated with k, Zi = NCS individual weight for i, and GiC = 1, if the quote containing i has worker characteristic C. Otherwise, GiC = 0.
The characteristic-proportion cells BkC are initially broken out by OES panel, wage interval, six-digit SOC code, and NCS sample area (24 NCS sample areas exist, which were referred to previously). Yet, if fewer than three NCS quotes are in the cell, it is collapsed and the characteristic proportion is recomputed with the use of the microdata from the collapsed cell. First, we collapse the NCS sample areas into census divisions, then census regions, and then the nation. Next, we collapse the six-digit SOC codes into MOGs. Finally, we collapse the MOGs together. If the final imputation cell has no quotes with the characteristic, we set the characteristic proportion to zero.
The variance of the mean wage estimator for the MWE program is the expected value of the squared deviation of the estimates from their expected value, which is defined as
![]()
where D = MWE domain; C = worker characteristic; s = sample; Pr(s) = probability of selecting s; ![]() = variance of the estimator
= variance of the estimator ![]() ;
; ![]() = mean wage estimator for the MWE program for D and C;
= mean wage estimator for the MWE program for D and C; ![]() = mean wage estimator for the MWE program for D and C, for the given sample s; and
= mean wage estimator for the MWE program for D and C, for the given sample s; and ![]() = expected value of the estimator
= expected value of the estimator ![]() , where
, where ![]() =
=![]() .
.
We cannot compute the variance directly because we only have one sample to work with, so we must estimate the variance. Several different methods can be used for estimating the variance, but they fit into two broad categories: linearization methods and replication methods.
One linearization method is the Taylor series method.7 It approximates the sample deviation as a linear function of the numerator and denominator of the mean wage estimator. We approximate the sampling variability by looking at how the units vary inside the sample, yet also considering the sample design.
The variance estimate for the OES mean wage estimator is a sum of two components. The first variance component measures the OES sample design’s contribution to the variance. A Taylor series variance estimator is used. Yet, the interval means are constant, so the Taylor series variance estimator only captures the variability from the OES sample design. The second variance component models the interval means’ contribution to the variance, which can vary by NCS sample. First, NCS microdata are used for creating an artificial population. Next, a regression model is created that relates the interval means of this population to auxiliary data. One output of the modeling process is the contribution of each regression variable to the model variance. The second variance component is the sum of these variance contributions.
One replication method is Fay’s BRR, mentioned earlier.8 First, we create an artificial set of new estimates, called replicate estimates. The distribution of these replicate estimates is used to model the true distribution of sample estimates, from which the variance can be estimated.
Recall that the mean wage estimator for the MWE program is the mean wage estimator for the OES program, with the inclusion of the characteristic proportion. Hence, for MWE variance estimation, we could start by considering the OES variance estimator. Yet, the OES variance estimator does not account for the sampling variability of the characteristic proportions. Accounting for this variability, of course, was not necessary for the OES program since the mean wage estimator for the OES program does not have a characteristic proportion. For the MWE variance estimator, to account for this extra component of variance, one can use a new linear function for the Taylor series. This possibility was investigated but was too complex to estimate.
The Fay’s BRR variance estimator, by comparison, is much simpler, and it can still capture all three sources of sampling variability for the mean wage estimator of the MWE program. The first source of sampling variability is from the OES sample design. Recall that for OES variance estimation, a Taylor series variance estimator is used for estimating the OES sample design’s contribution to the variance. For the MWE variance estimator, however, we use the Fay’s BRR variance estimator to capture the first variance contribution and we vary the OES sampling weights by replicate. The second source of sampling variability for the mean wage estimator for the MWE program is from the interval means, which can vary by NCS sample. Recall that for OES variance estimation, this source of sampling variability was estimated as the sum of regression-model variance components. For the MWE variance estimator, however, we use the Fay’s BRR variance estimator to capture the second variance contribution and we vary the NCS sampling weights in the initial interval mean formula by replicate. The third source of sampling variability for the mean wage estimator of the MWE program is from the characteristic proportions, which can vary by NCS sample. This third source is unique to the MWE program and does not exist in the OES program. For the MWE variance estimator, we use the Fay’s BRR variance estimator to capture the third variance contribution and we vary the NCS sampling weights in the characteristic-proportion formulas by replicate.
The Fay’s BRR estimator of the variance of the mean wage estimator for the MWE program is given by
![]()
where R = number of replicates; r = replicate number; ![]() = Fay’s BRR estimator of the variance of the estimator
= Fay’s BRR estimator of the variance of the estimator ![]() ;
; ![]() = mean wage estimator for the MWE program for domain D, characteristic C, and replicate r; and
= mean wage estimator for the MWE program for domain D, characteristic C, and replicate r; and ![]() = mean wage estimator for the MWE program for domain D and characteristic C. For each D and C, the estimates computed from the estimator
= mean wage estimator for the MWE program for domain D and characteristic C. For each D and C, the estimates computed from the estimator ![]() are called replicate estimates, and the estimate computed from the estimator
are called replicate estimates, and the estimate computed from the estimator ![]() is called the full-sample estimate.
is called the full-sample estimate.
Note that the mean squared deviation is multiplied by 4. This rescaling is done because the distribution of replicate estimates will be about half as wide as the true sampling distribution.
To compute a replicate estimate of the mean hourly wage for the MWE program, we use the same formula as that used for the full-sample estimate of the mean hourly wage for the MWE program, except that some, but not all, of the terms in the full-sample estimation formula are replaced by their replicate estimates. OES and NCS weights are replaced with their replicate weights.
The mean wage estimator for the MWE program for domain D, characteristic C, and replicate r is
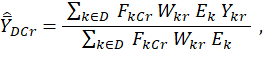
where ![]() = mean wage estimator for the MWE program for domain D, characteristic C, and replicate r; for OES interval data, k = OES estab-occ-interval and Ykr = rth replicate estimate of the NCS interval-mean wage used for k; for OES point data, k = OES individual wage record in an OES estab-occ and Ykr = OES individual wage rate for k; and for point data, this value Ykr is the same for all replicates. For the other variables, D = MWE estimation domain, which is an occupational domain in a geographic domain; C = worker characteristic; r = replicate number; FkCr = rth replicate estimate of the MWE characteristic proportion for C (used for k); Wkr = OES weight for the OES establishment containing k (adjusted for replicate r); and Ek = OES employment of k (this value is the same for all replicates).
= mean wage estimator for the MWE program for domain D, characteristic C, and replicate r; for OES interval data, k = OES estab-occ-interval and Ykr = rth replicate estimate of the NCS interval-mean wage used for k; for OES point data, k = OES individual wage record in an OES estab-occ and Ykr = OES individual wage rate for k; and for point data, this value Ykr is the same for all replicates. For the other variables, D = MWE estimation domain, which is an occupational domain in a geographic domain; C = worker characteristic; r = replicate number; FkCr = rth replicate estimate of the MWE characteristic proportion for C (used for k); Wkr = OES weight for the OES establishment containing k (adjusted for replicate r); and Ek = OES employment of k (this value is the same for all replicates).
The rth replicate estimate of the characteristic proportion is computed from NCS microdata as
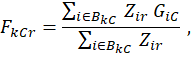
where i = individual wage record in an NCS quote; BkC = characteristic-proportion final imputation cell associated with k and C (the value BkC is the same for all replicates); Zir = NCS individual weight for i, adjusted for replicate r; and GiC = 1 if the quote containing i has worker characteristic C. Otherwise, GiC = 0 (this value is the same for all replicates).
If k is an estab-occ-interval, the rth replicate estimate Ykr of the NCS interval mean wage is computed in the following way. First, we use the same NCS input dataset as the full-sample estimate and modify the dataset the same way. Then we compute an initial interval mean as
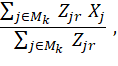
where j = individual wage record in an NCS quote; Mk = interval-mean cell, associated with k and C (this is the same for all replicates); Zjr = NCS individual weight for j, adjusted for replicate r; and Xj = NCS mean hourly wage for j (this is the same for all replicates).
This initial interval mean for replicate r is then adjusted with the same algorithm that was used for the full-sample estimate, yet with modifications. Some aspects of the algorithm can vary by OES and/or NCS sample. Thus, some of these aspects are allowed to vary by replicate, yet not all, to avoid too much complexity. For example, the ECI aging factors do not vary by replicate, even though they would vary by NCS sample.
For replicate r, if an OES establishment is sampled with certainty (probability 1), no adjustments are made to the OES establishment weight. For an OES noncertainty establishment, the OES establishment weight is either increased by 50 percent or decreased by 50 percent. For each NCS quote hit, the NCS individual weight is increased by 50 percent or decreased by 50 percent.
To define these perturbation patterns, first we partition the microdata into H variance strata (to be described later). Next, we split the sampling units in each variance stratum h into two roughly equal parts, called variance PSU 1 and variance PSU 2 (mentioned earlier). Then, for replicate r and variance stratum h, we upweight one variance PSU by 50 percent and downweight the other by 50 percent. The perturbations are not random but are chosen in a balanced fashion. Suppose we represented the perturbation choices as a matrix with R rows and H columns. For replicate r and stratum h, if PSU 1 is upweighted, let the matrix entry be 1; otherwise, let it be –1. Then the perturbation pattern is balanced whenever this matrix has orthogonal column vectors. That is, the inner product of all pairs of columns is always zero. The number R of replicates is always greater than or equal to the number H of strata, but typically R will be within a few units of H.
Ideally, the variance strata should be based on the first-stage sampling strata. But in some cases, we collapse the variance strata together; in others, we split them up. For example, we want each variance PSU in each variance stratum to have at least one sample unit. So we collapse the variance strata together until each stratum has at least two units. Sometimes, we collapse strata together simply to reduce the number H of strata. The fewer strata that exist, the fewer replicates we need, which speeds up running times because there are fewer replicate estimates to compute. Finally, in some cases, we do not have enough strata to accurately capture the sampling variability. For example, if only three strata exist, then there will be only four replicates. Yet, suppose the number of possible samples is much larger than four. Then using only four replicate estimates to approximate the true sample distribution of the mean wage estimates could underestimate the variance. Splitting up the variance strata increases the number and hence the diversity of the replicate estimates, which could counteract this bias in the variance estimate since it may be a better approximation of the true sampling distribution.
The replicate estimator for mean hourly wage for the MWE program has both NCS and OES terms and also three types of MWE domains: locality, state, and national. The NCS already uses Fay’s BRR, so for the NCS terms, we already have NCS variance strata and PSUs. Some of these NCS variance strata and PSUs are designed for NCS locality estimates, and some are designed for NCS national estimates. Hence, for each MWE domain and each NCS quote hit, we must decide if we should use the locality variance strata and PSUs or use the national variance strata and PSUs. For the OES program, Fay’s BRR was not used. Yet, the OES sampling strata were available. First, we let the OES variance strata for a MWE domain equal the OES sampling strata within the MWE domain. Many of these OES variance strata, however, are then collapsed together or spilt into pieces. Hence, the final MWE variance strata for a domain are a mixture of these three types of strata: NCS locality variance strata, NCS national variance strata, and the new OES variance strata.
For each NCS quote hit, we must decide whether to use its NCS locality variance stratum and PSU definition or its NCS national variance stratum and PSU definition. The choice we make for a quote hit is based on the scope of the MWE estimation domain, so it can vary by MWE domain. Suppose we are estimating mean wages for the MWE program for a domain that spans the nation. Then, we only use the NCS national variance strata and PSU definitions. On the other hand, suppose the MWE domain is in a single OES locality or a single state. Let A1 be the locality or the state containing the MWE domain, and let A2 be the NCS sample area that contains the given NCS quote hit. If A1 and A2 overlap, then we use the locality variance stratum and PSU definitions for that quote hit. Otherwise, we use the NCS national variance stratum and PSU definitions.
The approach just discussed for locality and state MWE domains was used primarily to solve a problem in which too few NCS sampling strata existed in the final characteristic-proportion imputation cell. Again, suppose A1 is the MWE domain and A2 is the NCS sample area containing the quote. Suppose A1 is a subset of A2, and we proceed to compute the replicate estimates for a characteristic proportion for the given quote. The initial characteristic-proportion imputation cell will be contained within this single NCS area A2. Suppose this initial imputation cell has at least three quotes; then no collapsing occurs. Unfortunately, this single area A2 has only five NCS sampling strata (and hence only five NCS national variance strata), which did not seem enough for reliably capturing the true within-cell variability. So for these cases, we elected instead to use the 44 locality variance strata that exist inside each NCS area. These 44 strata are industry poststrata and are used for computing locality variance estimates for other NCS programs (such as ECI and ECEC). This methodology also handles cases in which the characteristic-proportion cells are collapsed.
To get the OES variance strata for the MWE domain, we start with the OES sampling strata in the MWE domain, which are based on OES locality, state, industry, and panel. First, we may need to collapse some strata together, since for Fay’s BRR, we prefer at least two OES establishments per variance stratum. A within-cell nearest neighbor method is used. First, we create a collapse tree whose leaves are the OES sampling strata. If a stratum needs to be collapsed, we try to pair it with a neighboring donor stratum that shares the same parent. If no such donor can be found, we look for a neighboring donor that shares the same grandparent, and so on.
If the MWE domain is small, the domain may not have enough OES variance strata for reliably estimating the variance. So if possible, the strata are split by establishment size class and then by industry (defined by the North American Industry Classification System codes) until there are enough variance strata. Yet, the sparseness of the OES microdata and the requirement of at least two units per stratum often makes this effort impossible. Even if some splitting by size class and industry can occur, often after this process terminates, the MWE domain still has too few variance strata. If the MWE domain still has too few variance strata, we reject these final variance strata and try again. Yet, this time, we abandon the goal of splitting only by size class and industry. Rather, the establishments in the MWE domain are sorted, by size and industry, and then the first establishment is paired with the second, the third with the fourth, and so on. This pairing yields the most variance strata, although each stratum is no longer necessarily restricted to a single size class and industry. However, the MWE domain still may not have enough variance strata, simply because there are not enough OES establishments. Fortunately, many of these small MWE domains are too small to publish.
On the other hand, for many large MWE domains, far too many OES sampling strata are in the domain. If we used all of them, then the number R of replicates would be too large to allow us to compute all the replicate estimates in any reasonable time, and the storage requirements would be severe. So more collapsing of strata must occur until the total number H of strata (and hence R) is more tractable.
For locality MWE, all the collapsing just described is done first by panel, then state, and then industry. For state MWE, we also collapse by locality size class and by metropolitan or nonmetropolitan status. Yet, for state MWE, the collapse levels (industry groups, geographic objects, locality size classes, and metropolitan or nonmetropolitan status groups) are interleaved in the collapse tree, which allows us to achieve a decent balance. For example, we might first collapse by one industry level, then by one geographic level, and then by one locality size class level and so forth, and then repeat this cycle. The national MWE program, however, has three more geographic levels: states, census divisions, and census regions. To compensate, we removed some of the industry levels. Also, the order in which the levels are interleaved for national estimates is different from that for state estimates. The order matters because the higher a node is on the collapse tree, the more likely its information and, hence, its variability will be retained when we collapse from the bottom up.
Note that a new set of OES variance strata is defined for each MWE domain. This practice differs from that which is typically used in the NCS program, in which the variance strata are fixed for all NCS domains. For the NCS program, the number of sampling strata are small, so we used a fixed set. For the OES program, however, about 151,000 OES sampling strata (with OES microdata) exist. So for large MWE domains, such as two-digit SOC codes for national estimates, we could only get a manageable amount of strata by applying a huge amount of collapsing. Unfortunately, for small domains, such as a six-digit SOC code within a locality, the number of OES sampling strata (with microdata in the domain) is often very small, so we may want more strata rather than fewer strata. So making one fixed set of OES variance strata that would work for all MWE domain sizes would have been difficult. Hence, the OES variance strata were redefined for each MWE domain.
The variance estimate is a measure of mean squared deviation. However, the variance estimate is not directly comparable to the mean wage estimate because the mean wage is measured in dollars, whereas the mean squared deviation is measured in dollars squared. Hence, we often take the square root of the variance so that we have a value that is comparable to the mean wage estimate. The square root of the variance is called the standard error. The standard error often varies greatly across domains because of the size of the mean wage, not because of reliability issues. So the standard error is often represented instead as a percentage of the mean wage. This approach allows better comparisons across domains. This new value is called the percent relative standard error (%RSE). Tables 1–6 in the next section contain mean wages and %RSEs.
The standard error estimate can also be used to generate an estimated confidence interval as
![]()
where z depends on the desired confidence level. For example, for the 90-percent confidence level, z is about 1.645. To understand the estimated confidence interval, consider the following situation. Suppose the confidence level was 90 percent, and we could select all samples and compute their confidence intervals. Also, suppose these estimates were normally distributed. Then, we expect that 90 percent of these confidence intervals will contain the true population value. In reality, estimates usually are not normally distributed, but for large sample sizes, the normal distribution is a good approximation of the true distribution. The smaller the variance, the smaller the confidence interval and hence the more reliable the estimate.
A complete set of all mean wage estimates for the MWE program for May 2018 can be found at https://www.bls.gov/mwe/mwe-2018complete.xlsx. This Excel file was used to generate six custom tables for this article, tables 1–6. They can be found below. Tables 1–6 show mean hourly wages for the MWE program and their associated %RSEs, for a few domains and characteristics. Tables 1 and 2 show national estimates by occupational group (two-digit SOC code) and by worker characteristic. Tables 3 and 4 show state estimates for a single six-digit SOC code, cashiers. Tables 5 and 6 show state estimates for another six-digit SOC code, registered nurses.
| Occupational group | Union | Nonunion | Time-based pay | Incentive-based pay | Full time | Part time | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | |
| Management | — | — | 58.65 | 1.2 | 57.47 | 1.1 | 77.02 | 6.4 | 59.07 | 1.2 | — | — |
| Business and financial operations | 33.31 | 2.5 | 36.84 | 0.4 | 35.63 | 0.3 | 56.01 | 3.1 | 37.12 | 0.4 | 22.30 | 8.2 |
| Computer and mathematical | 43.90 | 4.1 | 43.89 | 0.2 | 43.79 | 0.2 | 54.15 | 9.4 | 44.27 | 0.2 | — | — |
| Architecture and engineering | 44.04 | 4.9 | 41.43 | 0.5 | 41.45 | 0.4 | — | — | 41.99 | 0.3 | 33.20 | 4.0 |
| Life, physical, and social science | 42.21 | 3.4 | 34.78 | 1.0 | 35.94 | 0.7 | — | — | 36.76 | 0.5 | 31.01 | 3.6 |
| Community and social service | 29.93 | 1.5 | 21.41 | 0.6 | 23.55 | 0.2 | — | — | 24.33 | 0.6 | 19.33 | 2.8 |
| Legal | 42.25 | 4.5 | 53.06 | 1.7 | 52.04 | 1.5 | — | — | 53.15 | 1.8 | 41.89 | 10.9 |
| Education, training, and library | — | — | 24.51 | 0.5 | — | — | — | — | — | — | — | — |
| Arts, design, entertainment, sports, and media | — | — | 27.15 | 1.0 | 28.41 | 0.8 | — | — | 31.45 | 0.8 | — | — |
| Healthcare practitioners and technical | 48.28 | 4.9 | 37.89 | 1.3 | 38.86 | 0.8 | — | — | 40.50 | 0.9 | 35.19 | 1.8 |
| Healthcare support | 19.92 | 2.6 | 14.93 | 0.8 | 15.50 | 0.6 | — | — | 16.26 | 0.8 | 13.92 | 1.7 |
| Protective service | 30.24 | 2.1 | 18.07 | 1.6 | 22.90 | 0.4 | — | — | 24.98 | 0.5 | 14.72 | 2.7 |
| Food preparation and serving related | 17.79 | 2.2 | 11.87 | 3.9 | 12.24 | 3.6 | 17.83 | 6.2 | 14.33 | 1.9 | 10.93 | 5.1 |
| Building and grounds cleaning and maintenance | 19.21 | 1.4 | 13.39 | 1.8 | 14.35 | 1.4 | 17.74 | 5.7 | 15.12 | 1.2 | 12.23 | 2.8 |
| Personal care and service | 17.69 | 2.3 | 13.17 | 2.2 | 13.34 | 2.1 | 16.48 | 4.9 | 14.52 | 1.5 | 12.55 | 3.0 |
| Sales and related | 15.23 | 2.9 | 20.29 | 0.9 | 16.68 | 1.3 | 36.41 | 1.8 | 26.26 | 0.7 | 11.19 | 3.1 |
| Office and administrative support | 22.21 | 1.0 | 18.12 | 0.5 | 18.51 | 0.4 | 19.91 | 2.4 | 19.77 | 0.3 | 13.21 | 2.2 |
| Construction and extraction | 33.41 | 0.9 | 21.66 | 0.7 | 24.56 | 0.2 | 28.57 | 10.8 | 24.88 | 0.3 | 18.84 | 6.0 |
| Installation, maintenance, and repair | 31.74 | 1.2 | 21.56 | 0.4 | 23.28 | 0.2 | 25.87 | 2.5 | 24.02 | 0.3 | 14.77 | 4.3 |
| Production | 23.30 | 1.2 | 17.99 | 0.5 | 18.82 | 0.4 | 18.51 | 6.6 | 19.35 | 0.3 | 11.97 | 2.6 |
| Transportation and material moving | 24.82 | 1.7 | 16.20 | 0.9 | 18.12 | 0.7 | 21.38 | 3.0 | 19.84 | 0.6 | 13.68 | 2.1 |
| Notes: For definitions of worker characteristics terms, see “Frequently asked questions” at https://www.bls.gov/mwe/faq.htm. Dash indicates data failed to meet publication criteria. %RSE = percent relative standard error. Source: “2018 modeled wage estimates,” National Compensation Survey (U.S. Bureau of Labor Statistics, August 2019), https://www.bls.gov/mwe/mwe-2018complete.xlsx. | ||||||||||||
| Occupational group | Value | Work level | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| Management | Mean | — | — | — | — | — | 16.15 | 23.57 | 28.11 | 35.76 | 39.52 | 53.97 | 72.01 | 81.42 |
| %RSE | — | — | — | — | — | 4.10 | 5.80 | 3.10 | 2.00 | 3.70 | 1.80 | 2.80 | 4.20 | |
| Business and financial operations | Mean | — | — | — | — | 20.78 | 21.30 | 23.78 | 28.68 | 34.75 | 44.32 | 52.81 | 66.35 | 90.13 |
| %RSE | — | — | — | — | 6.20 | 2.90 | 2.50 | 1.60 | 1.20 | 2.40 | 1.80 | 2.70 | 11.30 | |
| Computer and mathematical | Mean | — | — | — | — | 20.66 | 22.08 | 27.48 | 34.02 | 40.16 | 47.49 | 53.32 | 69.13 | 77.59 |
| %RSE | — | — | — | — | 4.50 | 1.70 | 1.80 | 2.40 | 1.30 | 2.50 | 0.90 | 1.50 | 1.90 | |
| Architecture and engineering | Mean | — | — | — | 18.84 | 22.68 | 23.90 | 29.66 | 34.22 | 37.99 | 45.51 | 51.30 | 66.49 | 81.03 |
| %RSE | — | — | — | 2.20 | 3.30 | 1.70 | 1.90 | 1.60 | 1.50 | 3.00 | 1.60 | 2.50 | 2.50 | |
| Life, physical, and social science | Mean | — | — | 14.31 | 17.29 | 19.58 | 23.73 | 24.99 | 33.95 | 36.37 | 37.11 | 48.69 | 65.17 | — |
| %RSE | — | — | 2.90 | 4.00 | 2.40 | 3.20 | 2.10 | 3.50 | 1.90 | 3.40 | 2.40 | 3.90 | — | |
| Community and social service | Mean | — | — | — | — | 14.96 | 17.52 | 21.31 | 25.42 | 30.75 | 32.72 | 36.68 | — | — |
| %RSE | — | — | — | — | 2.40 | 1.90 | 1.50 | 2.60 | 1.20 | 4.80 | 4.00 | — | — | |
| Legal | Mean | — | — | — | — | — | 21.68 | 25.41 | 35.61 | 35.49 | 45.55 | 46.59 | 59.44 | 98.21 |
| %RSE | — | — | — | — | — | 5.10 | 2.60 | 7.10 | 3.20 | 10.10 | 4.00 | 3.00 | 10.80 | |
| Education, training, and library | Mean | — | 9.89 | 12.90 | 14.36 | 15.44 | 15.75 | 21.45 | 25.82 | 31.47 | 38.83 | 46.49 | 66.47 | 95.04 |
| %RSE | — | 8.30 | 3.50 | 2.20 | 3.00 | 2.00 | 3.20 | 4.10 | 0.60 | 3.20 | 2.00 | 4.40 | 5.00 | |
| Arts, design, entertainment, sports, and media | Mean | — | — | — | 13.09 | 15.78 | 18.52 | 23.94 | 30.38 | 34.93 | 43.21 | 50.81 | — | — |
| %RSE | — | — | — | 2.00 | 2.80 | 2.30 | 2.70 | 4.00 | 1.40 | 2.50 | 3.20 | — | — | |
| Healthcare practitioners and technical | Mean | — | 12.77 | 14.59 | 15.56 | 21.29 | 23.52 | 30.00 | 32.22 | 37.53 | 45.26 | 58.25 | 98.40 | — |
| %RSE | — | 9.70 | 3.50 | 1.80 | 3.60 | 2.00 | 1.20 | 1.90 | 0.90 | 2.40 | 2.50 | 6.70 | — | |
| Healthcare support | Mean | — | 12.30 | 13.06 | 15.53 | 19.36 | 24.58 | 29.11 | — | 37.50 | — | — | — | — |
| %RSE | — | 3.30 | 1.10 | 0.80 | 2.20 | 2.10 | 1.60 | — | 2.60 | — | — | — | — | |
| Protective service | Mean | 11.93 | 12.64 | 13.57 | 15.62 | 20.76 | 27.22 | 32.18 | 37.01 | 41.54 | 46.77 | — | — | — |
| %RSE | 3.30 | 4.20 | 2.20 | 1.90 | 4.00 | 3.30 | 1.40 | 3.30 | 1.80 | 5.90 | — | — | — | |
| Food preparation and serving related | Mean | 10.14 | 10.61 | 12.16 | 14.11 | 16.65 | 21.55 | 25.19 | 31.36 | 33.67 | — | — | — | — |
| %RSE | 6.30 | 5.70 | 3.00 | 1.80 | 3.10 | 4.00 | 3.00 | 4.40 | 7.50 | — | — | — | — | |
| Building and grounds cleaning and maintenance | Mean | 10.85 | 12.39 | 14.80 | 17.01 | 21.63 | 23.12 | 24.09 | — | — | — | — | — | — |
| %RSE | 4.70 | 2.50 | 1.40 | 2.30 | 3.40 | 3.70 | 3.80 | — | — | — | — | — | — | |
| Personal care and service | Mean | 10.45 | 10.42 | 11.82 | 14.12 | 17.11 | 22.51 | 26.46 | 29.00 | 42.03 | — | — | — | — |
| %RSE | 7.90 | 6.00 | 2.70 | 2.00 | 3.00 | 3.90 | 3.70 | 10.50 | 2.80 | — | — | — | — | |
| Sales and related | Mean | 10.11 | 10.85 | 12.17 | 17.67 | 22.40 | 27.84 | 33.71 | 39.00 | 56.45 | 61.66 | 75.44 | — | — |
| %RSE | 5.60 | 3.50 | 2.40 | 2.70 | 2.10 | 3.60 | 2.30 | 4.30 | 2.60 | 5.90 | 8.40 | — | — | |
| Office and administrative support | Mean | 11.49 | 11.92 | 13.75 | 17.13 | 20.20 | 24.86 | 30.53 | 34.61 | — | — | — | — | — |
| %RSE | 3.20 | 2.50 | 1.30 | 0.70 | 0.60 | 0.80 | 1.20 | 1.70 | — | — | — | — | — | |
| Construction and extraction | Mean | 13.74 | 15.71 | 16.98 | 19.28 | 24.63 | 29.85 | 32.80 | 36.73 | 50.03 | — | — | — | — |
| %RSE | 7.50 | 2.20 | 1.50 | 1.50 | 1.10 | 1.50 | 1.80 | 4.00 | 3.90 | — | — | — | — | |
| Installation, maintenance, and repair | Mean | 11.51 | 14.19 | 14.73 | 17.11 | 20.76 | 26.30 | 30.99 | 37.37 | 40.54 | — | — | — | — |
| %RSE | 3.50 | 3.40 | 2.20 | 1.90 | 1.50 | 1.10 | 1.10 | 3.20 | 3.50 | — | — | — | — | |
| Production | Mean | 11.04 | 12.40 | 15.60 | 18.38 | 20.05 | 25.44 | 31.19 | 36.30 | 39.02 | — | — | — | — |
| %RSE | 3.50 | 1.50 | 1.10 | 0.90 | 1.00 | 1.00 | 2.30 | 2.30 | 3.70 | — | — | — | — | |
| Transportation and material moving | Mean | 11.59 | 13.82 | 16.67 | 21.76 | 24.45 | 28.00 | 33.75 | 39.74 | 62.39 | — | — | — | — |
| %RSE | 3.20 | 1.70 | 1.30 | 1.40 | 1.50 | 2.70 | 3.50 | 4.90 | 8.30 | — | — | — | — | |
| Notes: Dash indicates data failed to meet publication criteria. %RSE = percent relative standard error. Source: “2018 modeled wage estimates,” National Compensation Survey (U.S. Bureau of Labor Statistics, August 2019), https://www.bls.gov/mwe/mwe-2018complete.xlsx. | ||||||||||||||
| State | Union | Nonunion | Time-based pay | Full time | Part time | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | |
| United States | 13.19 | 2.0 | 10.90 | 3.3 | 11.15 | 3.1 | 12.16 | 2.1 | 10.77 | 3.6 |
| Alabama | — | — | 9.91 | 7.0 | 9.88 | 7.2 | 10.63 | 5.5 | 9.39 | 8.8 |
| Alaska | 16.81 | 4.0 | 12.50 | 1.0 | 13.43 | 1.4 | — | — | 13.34 | 1.6 |
| Arizona | 14.12 | 6.8 | 11.82 | 1.0 | 12.00 | 0.5 | — | — | 11.73 | 1.0 |
| Arkansas | — | — | 10.18 | 1.6 | 10.18 | 1.6 | — | — | 9.90 | 1.8 |
| California | — | — | 12.16 | 0.7 | 13.18 | 0.4 | — | — | 13.05 | 1.0 |
| Colorado | 13.89 | 4.1 | 12.30 | 0.9 | 12.42 | 0.9 | 13.56 | 1.5 | 11.90 | 1.0 |
| Connecticut | 12.38 | 3.5 | 12.08 | 1.5 | 12.15 | 0.8 | 13.31 | 5.8 | 11.85 | 1.3 |
| Delaware | 10.63 | 5.4 | 10.69 | 2.1 | 10.67 | 1.9 | 12.20 | 2.3 | 10.42 | 2.5 |
| District of Columbia | 15.73 | 2.0 | 13.80 | 1.7 | 14.27 | 1.7 | — | — | 14.14 | 1.9 |
| Florida | 11.00 | 4.4 | 10.50 | 3.1 | 10.50 | 3.2 | 12.12 | 1.8 | 9.94 | 4.0 |
| Georgia | — | — | 10.09 | 6.4 | 9.98 | 7.2 | 11.12 | 3.5 | 9.45 | 9.4 |
| Hawaii | — | — | 11.74 | 0.9 | 12.48 | 0.7 | — | — | 12.38 | 1.3 |
| Idaho | 11.76 | 7.8 | 10.61 | 4.6 | 10.69 | 4.6 | 11.84 | 4.5 | 10.26 | 5.4 |
| Illinois | 13.63 | 4.2 | 10.86 | 2.2 | 11.22 | 1.9 | 12.43 | 3.3 | 10.79 | 2.2 |
| Indiana | 11.23 | 3.6 | 10.00 | 7.1 | 10.15 | 6.5 | 11.45 | 4.5 | 9.76 | 7.4 |
| Iowa | 9.23 | 14.3 | 10.66 | 4.2 | 10.49 | 4.8 | 11.44 | 4.6 | 9.94 | 6.0 |
| Kansas | 9.04 | 13.5 | 10.58 | 6.0 | 10.37 | 6.5 | 11.17 | 4.5 | 9.95 | 8.1 |
| Kentucky | — | — | 9.82 | 8.9 | 9.79 | 9.1 | 10.66 | 6.8 | 9.23 | 11.1 |
| Louisiana | — | — | 9.51 | 9.6 | 9.50 | 9.6 | — | — | 9.24 | 10.4 |
| Maine | — | — | 11.11 | 0.9 | 11.14 | 0.4 | 12.41 | 7.1 | 10.91 | 0.8 |
| Maryland | 13.53 | 5.5 | 11.13 | 1.5 | 11.49 | 0.9 | 13.34 | 15.0 | 11.29 | 1.0 |
| Massachusetts | 12.88 | 3.2 | 12.61 | 0.7 | 12.62 | 0.3 | 14.12 | 3.5 | 12.25 | 0.8 |
| Michigan | 12.85 | 1.9 | 10.83 | 0.8 | 11.16 | 0.5 | 12.02 | 1.5 | 10.81 | 0.9 |
| Minnesota | — | — | 11.97 | 0.4 | 11.89 | 0.5 | 13.11 | 1.8 | 11.28 | 0.3 |
| Mississippi | — | — | 9.44 | 10.1 | 9.40 | 10.2 | 10.09 | 7.9 | 9.01 | 11.9 |
| Missouri | — | — | 10.77 | 3.8 | 10.60 | 4.2 | 11.67 | 4.4 | 9.98 | 5.3 |
| Montana | 11.48 | 5.1 | 10.98 | 2.4 | 11.01 | 2.4 | 12.03 | 2.9 | 10.62 | 2.8 |
| Nebraska | 10.34 | 5.5 | 11.16 | 0.9 | 11.09 | 0.8 | — | — | 10.67 | 1.0 |
| Nevada | 12.84 | 8.4 | 11.05 | 4.2 | 11.19 | 4.1 | 12.48 | 4.2 | 10.70 | 4.9 |
| New Hampshire | 11.65 | 4.1 | 10.85 | 4.1 | 10.95 | 3.6 | 12.46 | 3.9 | 10.59 | 4.1 |
| New Jersey | 11.39 | 2.7 | 11.16 | 2.3 | 11.23 | 1.9 | 13.57 | 5.8 | 10.83 | 2.1 |
| New Mexico | 10.84 | 6.6 | 10.59 | 4.5 | 10.60 | 4.5 | 11.63 | 4.5 | 10.23 | 5.2 |
| New York | 12.98 | 2.2 | 11.97 | 1.2 | 12.24 | 0.6 | 13.45 | 3.6 | 11.95 | 0.9 |
| North Carolina | 10.40 | 8.9 | 9.85 | 8.2 | 9.87 | 8.2 | 11.51 | 5.8 | 9.33 | 9.9 |
| North Dakota | 10.96 | 13.8 | 12.18 | 1.7 | 12.09 | 1.9 | 13.20 | 2.0 | 10.93 | 3.1 |
| Ohio | 11.67 | 3.1 | 10.46 | 3.9 | 10.63 | 3.5 | 12.39 | 2.7 | 10.06 | 4.3 |
| Oklahoma | — | — | 10.00 | 7.6 | 10.03 | 7.6 | 10.84 | 6.0 | 9.61 | 8.8 |
| Oregon | 16.35 | 2.0 | 11.91 | 0.6 | 12.50 | 0.7 | — | — | 12.45 | 1.2 |
| Pennsylvania | 10.43 | 6.8 | 10.12 | 6.9 | 10.12 | 6.7 | 12.10 | 6.3 | 9.78 | 7.8 |
| Rhode Island | 12.08 | 4.7 | 12.07 | 1.4 | 12.07 | 1.1 | 13.82 | 5.4 | 11.61 | 1.2 |
| South Carolina | 9.86 | 8.8 | 9.68 | 7.8 | 9.69 | 7.8 | 10.91 | 6.0 | 9.34 | 9.0 |
| South Dakota | 9.89 | 6.5 | 10.90 | 1.2 | 10.79 | 1.2 | 11.54 | 2.6 | 10.37 | 1.3 |
| Tennessee | — | — | 10.27 | 6.7 | 10.23 | 6.8 | 11.18 | 4.9 | 9.54 | 8.8 |
| Texas | — | — | 10.53 | 4.7 | 10.56 | 4.7 | — | — | 10.23 | 4.8 |
| Utah | 12.42 | 9.5 | 10.95 | 4.2 | 11.04 | 4.1 | 12.28 | 4.0 | 10.55 | 5.1 |
| Vermont | — | — | 12.07 | 1.2 | 12.17 | 1.0 | 13.33 | 7.1 | 11.76 | 1.9 |
| Virginia | 12.82 | 3.3 | 10.36 | 6.1 | 10.58 | 5.6 | 11.90 | 4.3 | 10.29 | 6.2 |
| Washington | — | — | 13.10 | 0.5 | 14.09 | 0.7 | 15.08 | 1.9 | 13.59 | 2.3 |
| West Virginia | 10.55 | 2.8 | 10.25 | 1.7 | 10.26 | 1.7 | 11.40 | 2.6 | 9.95 | 1.9 |
| Wisconsin | 11.34 | 3.5 | 10.33 | 5.8 | 10.47 | 5.2 | 11.93 | 2.8 | 9.99 | 6.4 |
| Wyoming | 11.74 | 6.4 | 11.04 | 4.3 | 11.09 | 4.3 | 12.19 | 4.4 | 10.66 | 5.0 |
| Notes: For definitions of worker characteristics terms, see “Frequently asked questions” at https://www.bls.gov/mwe/faq.htm. Dash indicates data failed to meet publication criteria. %RSE = percent relative standard error. Source: “2018 modeled wage estimates,” National Compensation Survey (U.S. Bureau of Labor Statistics, August 2019), https://www.bls.gov/mwe/mwe-2018complete.xlsx. | ||||||||||
| State | Level 1 | Level 2 | Level 3 | |||
|---|---|---|---|---|---|---|
| Mean | %RSE | Mean | %RSE | Mean | %RSE | |
| United States | 10.22 | 5.0 | 10.76 | 3.7 | 11.51 | 3.4 |
| Alabama | 9.91 | 7.6 | 9.24 | 10.2 | 9.32 | 9.2 |
| Alaska | — | — | 13.01 | 3.6 | 14.11 | 5.4 |
| Arizona | — | — | 11.53 | 1.9 | 12.29 | 2.1 |
| Arkansas | 9.67 | 2.3 | 9.86 | 2.0 | 10.36 | 1.8 |
| California | — | — | 12.74 | 1.3 | 13.42 | 3.9 |
| Colorado | 10.80 | 1.7 | 12.02 | 6.0 | 13.19 | 2.4 |
| Connecticut | 11.48 | 1.4 | 11.77 | 2.5 | 12.98 | 3.6 |
| Delaware | 9.25 | 4.8 | 10.71 | 2.7 | 10.46 | 7.4 |
| District of Columbia | 12.84 | 0.3 | 14.12 | 2.3 | 15.75 | 8.3 |
| Florida | 9.23 | 7.1 | 10.44 | 3.5 | 10.25 | 4.5 |
| Georgia | 8.60 | 14.2 | 9.74 | 9.2 | 9.59 | 8.1 |
| Hawaii | — | — | 12.06 | 3.8 | 13.21 | 5.5 |
| Idaho | 9.23 | 11.1 | 10.59 | 7.0 | 11.35 | 6.4 |
| Illinois | — | — | 10.44 | 3.1 | 12.19 | 4.5 |
| Indiana | 9.98 | 6.4 | 9.69 | 8.3 | 10.72 | 4.9 |
| Iowa | 9.85 | 7.0 | 10.02 | 6.5 | 11.45 | 11.0 |
| Kansas | 9.55 | 8.6 | 9.83 | 7.8 | 11.79 | 11.5 |
| Kentucky | 9.74 | 9.2 | 9.10 | 12.5 | 9.23 | 11.4 |
| Louisiana | 9.04 | 11.3 | 9.15 | 11.3 | 9.70 | 8.5 |
| Maine | — | — | 10.84 | 1.7 | 11.67 | 4.7 |
| Maryland | 10.58 | 2.9 | 11.25 | 2.2 | 12.78 | 12.6 |
| Massachusetts | 12.23 | 1.2 | 12.10 | 0.8 | 12.75 | 2.8 |
| Michigan | 10.42 | 0.4 | 10.79 | 1.2 | 11.65 | 10.0 |
| Minnesota | 11.08 | 1.8 | 10.98 | 1.1 | — | — |
| Mississippi | 9.54 | 9.8 | 8.92 | 13.0 | 9.00 | 11.8 |
| Missouri | 9.83 | 6.2 | 10.02 | 5.8 | 11.72 | 10.6 |
| Montana | 9.75 | 7.2 | 10.91 | 5.1 | 11.63 | 4.1 |
| Nebraska | 10.51 | 1.3 | 10.72 | 2.1 | 11.92 | 5.2 |
| Nevada | 9.34 | 11.2 | 11.01 | 8.6 | 11.95 | 6.5 |
| New Hampshire | 10.54 | 3.9 | 10.21 | 5.4 | 11.85 | 2.5 |
| New Jersey | 10.62 | 4.7 | 10.71 | 2.2 | 11.69 | 3.4 |
| New Mexico | 9.31 | 10.6 | 10.58 | 6.7 | 11.26 | 6.3 |
| New York | 11.79 | 1.7 | 11.68 | 0.8 | 12.72 | 3.6 |
| North Carolina | 8.61 | 14.6 | 9.76 | 8.4 | 9.61 | 10.2 |
| North Dakota | 10.52 | 4.0 | 11.11 | 5.5 | 13.39 | 5.4 |
| Ohio | 9.96 | 4.4 | 10.15 | 4.5 | 10.56 | 3.6 |
| Oklahoma | 9.25 | 10.0 | 9.49 | 9.7 | 10.21 | 6.7 |
| Oregon | — | — | 12.43 | 3.5 | 12.84 | 4.8 |
| Pennsylvania | 9.02 | 11.4 | 9.88 | 7.9 | 10.74 | 6.5 |
| Rhode Island | 11.68 | 2.1 | 11.43 | 1.0 | 12.26 | 4.8 |
| South Carolina | 8.65 | 13.3 | 9.66 | 7.9 | 9.52 | 9.5 |
| South Dakota | 10.33 | 2.1 | 10.47 | 2.4 | 11.50 | 7.3 |
| Tennessee | 10.07 | 7.9 | 9.40 | 10.3 | 9.54 | 9.7 |
| Texas | — | — | 10.10 | 7.1 | 10.15 | 6.8 |
| Utah | 9.24 | 11.5 | 10.93 | 8.0 | 11.73 | 6.4 |
| Vermont | 11.39 | 0.2 | 11.94 | 4.8 | 12.82 | 2.1 |
| Virginia | 9.19 | 10.7 | 10.61 | 5.8 | 10.33 | 8.3 |
| Washington | — | — | 13.96 | 1.2 | 14.75 | 2.2 |
| West Virginia | 9.50 | 2.7 | 10.18 | 2.1 | 10.16 | 3.5 |
| Wisconsin | 10.04 | 5.5 | 10.03 | 6.8 | 10.71 | 4.8 |
| Wyoming | 9.32 | 11.8 | 11.01 | 8.3 | 11.92 | 7.6 |
| Notes: Dash indicates data failed to meet publication criteria. %RSE = percent relative standard error. Source: “2018 modeled wage estimates,” National Compensation Survey (U.S. Bureau of Labor Statistics, August 2019), https://www.bls.gov/mwe/mwe-2018complete.xlsx. | ||||||
| State | Union | Nonunion | Time-based pay | Full time | Part time | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | Mean | %RSE | |
| United States | 46.88 | 1.3 | 33.87 | 0.60 | 36.11 | 0.1 | 35.41 | 0.7 | 38.24 | 1.7 |
| Alabama | — | — | 28.25 | 0.30 | 28.39 | 0.3 | 28.56 | 1.3 | 27.65 | 6.0 |
| Alaska | 44.33 | 2.3 | 41.27 | 2.40 | 42.52 | 0.4 | 41.35 | 2.6 | 45.46 | 6.4 |
| Arizona | — | — | 36.12 | 0.80 | 36.76 | 0.4 | 36.17 | 1.3 | 38.96 | 3.0 |
| Arkansas | — | — | 28.59 | 0.30 | 28.60 | 0.3 | 28.45 | 0.6 | 29.16 | 2.0 |
| California | 57.89 | 2.0 | 43.03 | 1.20 | 51.26 | 0.3 | 48.72 | 1.0 | 56.32 | 1.8 |
| Colorado | 41.48 | 6.9 | 34.82 | 1.40 | 35.46 | 0.3 | 35.59 | 1.3 | 34.82 | 6.9 |
| Connecticut | 39.15 | 1.7 | 38.67 | 1.40 | 38.87 | 0.4 | 39.75 | 1.4 | 37.05 | 2.5 |
| Delaware | 40.07 | 3.2 | 34.80 | 3.00 | 35.75 | 0.3 | 36.05 | 1.8 | 34.48 | 6.7 |
| District of Columbia | — | — | 39.95 | 1.70 | 44.19 | 0.8 | 41.95 | 1.2 | 50.28 | 1.5 |
| Florida | — | — | 31.28 | 0.50 | 31.56 | 0.5 | 31.63 | 0.6 | 31.25 | 2.4 |
| Georgia | — | — | 32.73 | 0.30 | 32.95 | 0.3 | 33.50 | 1.6 | 31.32 | 5.2 |
| Hawaii | 49.18 | 2.7 | 45.83 | 3.80 | 47.10 | 1.0 | 44.76 | 4.4 | 50.60 | 4.2 |
| Idaho | 34.51 | 7.4 | 31.81 | 1.00 | 32.03 | 0.6 | 32.31 | 0.9 | 30.60 | 3.7 |
| Illinois | 42.87 | 3.4 | 34.85 | 0.70 | 35.36 | 0.4 | 35.50 | 1.1 | 34.85 | 5.0 |
| Indiana | 38.10 | 6.3 | 30.25 | 1.70 | 31.00 | 0.2 | 30.59 | 1.1 | 32.24 | 2.5 |
| Iowa | 28.82 | 3.9 | 28.12 | 0.50 | 28.19 | 0.3 | 28.10 | 1.1 | 28.46 | 3.2 |
| Kansas | 29.72 | 4.6 | 28.96 | 0.60 | 29.04 | 0.2 | 28.91 | 1.1 | 29.41 | 3.1 |
| Kentucky | — | — | 30.03 | 0.20 | 30.13 | 0.2 | 30.12 | 1.6 | 30.23 | 7.3 |
| Louisiana | — | — | 30.37 | 1.10 | 30.49 | 1.1 | 30.62 | 0.9 | 30.08 | 4.0 |
| Maine | 33.64 | 4.6 | 31.07 | 6.80 | 32.31 | 0.5 | 33.84 | 1.6 | 30.20 | 2.4 |
| Maryland | 41.44 | 6.2 | 35.43 | 2.00 | 36.68 | 0.4 | 36.34 | 1.0 | 37.86 | 2.7 |
| Massachusetts | 51.26 | 2.2 | 41.54 | 1.30 | 44.19 | 0.3 | 43.86 | 1.5 | 44.66 | 1.9 |
| Michigan | 36.84 | 3.5 | 33.70 | 1.20 | 34.18 | 0.2 | 34.47 | 0.9 | 33.36 | 2.8 |
| Minnesota | 41.41 | 3.6 | 37.27 | 0.70 | 37.77 | 0.2 | 34.43 | 1.9 | 40.47 | 1.0 |
| Mississippi | — | — | 27.72 | 0.40 | 27.79 | 0.4 | 28.17 | 1.2 | — | — |
| Missouri | 33.15 | 5.9 | 30.84 | 0.90 | 31.03 | 0.3 | 31.20 | 0.9 | 30.78 | 2.2 |
| Montana | 33.45 | 8.0 | 32.00 | 0.80 | 32.12 | 0.4 | 32.08 | 0.8 | 32.34 | 4.0 |
| Nebraska | 31.37 | 4.1 | 30.80 | 0.70 | 30.86 | 0.4 | 30.70 | 0.7 | 31.30 | 1.8 |
| Nevada | 50.58 | 3.0 | 39.12 | 2.20 | 40.94 | 0.4 | 41.01 | 1.1 | 40.61 | 6.2 |
| New Hampshire | 37.31 | 3.0 | 34.20 | 1.30 | 34.88 | 0.4 | 35.00 | 2.7 | 34.69 | 4.1 |
| New Jersey | 41.70 | 1.7 | 38.76 | 0.70 | 39.71 | 0.3 | 39.97 | 1.0 | 39.03 | 2.6 |
| New Mexico | 36.94 | 7.3 | 33.95 | 1.00 | 34.19 | 0.6 | 34.36 | 1.1 | 33.25 | 5.5 |
| New York | 44.10 | 3.3 | 39.74 | 1.80 | 41.11 | 0.4 | 40.63 | 0.8 | 42.39 | 2.0 |
| North Carolina | — | — | 30.82 | 0.20 | 30.83 | 0.2 | 30.75 | 0.6 | 31.26 | 2.8 |
| North Dakota | 31.54 | 3.5 | 31.35 | 0.60 | 31.38 | 0.3 | 31.05 | 0.6 | 32.26 | 1.8 |
| Ohio | 37.39 | 6.5 | 31.12 | 1.90 | 31.88 | 0.2 | 31.44 | 1.1 | 32.94 | 2.1 |
| Oklahoma | — | — | 30.00 | 0.30 | 30.03 | 0.3 | 30.01 | 0.6 | 30.12 | 2.1 |
| Oregon | 44.42 | 2.1 | 43.01 | 2.30 | 43.63 | 0.3 | 42.36 | 2.2 | 46.72 | 5.2 |
| Pennsylvania | 38.09 | 1.4 | 32.61 | 2.40 | 33.80 | 0.3 | 33.78 | 0.6 | 33.41 | 2.6 |
| Rhode Island | 41.39 | 5.1 | 36.98 | 0.90 | 37.52 | 0.7 | 36.31 | 4.0 | 39.15 | 4.1 |
| South Carolina | — | — | 30.62 | 0.30 | 30.96 | 0.3 | 31.00 | 0.6 | 30.94 | 2.5 |
| South Dakota | 28.36 | 4.7 | 27.52 | 0.50 | 27.60 | 0.3 | 27.52 | 1.2 | 27.82 | 3.3 |
| Tennessee | — | — | 29.06 | 0.30 | 29.12 | 0.3 | 29.22 | 1.4 | 28.74 | 6.5 |
| Texas | — | — | 34.69 | 0.20 | 34.79 | 0.2 | 35.08 | 0.4 | 32.77 | 2.9 |
| Utah | 33.41 | 6.6 | 31.17 | 0.70 | 31.35 | 0.3 | 31.23 | 0.8 | 32.09 | 5.1 |
| Vermont | 33.53 | 4.9 | 32.48 | 5.30 | 33.02 | 0.6 | 34.35 | 2.1 | 30.90 | 2.1 |
| Virginia | — | — | 32.45 | 0.90 | 33.18 | 0.3 | 32.91 | 0.5 | 34.36 | 1.8 |
| Washington | 44.61 | 1.9 | 33.76 | 1.70 | 39.50 | 0.5 | 39.02 | 1.7 | 40.65 | 4.1 |
| West Virginia | — | — | 29.20 | 0.30 | 29.25 | 0.3 | 29.44 | 0.6 | 28.42 | 3.0 |
| Wisconsin | 38.98 | 5.8 | 33.29 | 2.30 | 34.12 | 0.2 | 33.47 | 1.1 | 35.58 | 1.8 |
| Wyoming | 34.12 | 7.9 | 31.49 | 1.10 | 31.63 | 0.9 | 31.57 | 1.2 | 32.36 | 4.5 |
| Notes: For definitions of worker characteristics terms, see “Frequently asked questions” at https://www.bls.gov/mwe/faq.htm. Dash indicates data failed to meet publication criteria. %RSE = percent relative standard error. Source: “2018 modeled wage estimates,” National Compensation Survey (U.S. Bureau of Labor Statistics, August 2019), https://www.bls.gov/mwe/mwe-2018complete.xlsx. | ||||||||||
| State | Value | Work level | ||||
|---|---|---|---|---|---|---|
| 7 | 8 | 9 | 10 | 11 | ||
| United States | Mean | 29.23 | 33.11 | 36.19 | 40.82 | 49.42 |
| %RSE | 3.30 | 2.60 | 0.80 | 3.40 | 3.60 | |
| Alabama | Mean | — | 27.10 | 27.97 | — | — |
| %RSE | — | 4.70 | 1.10 | — | — | |
| Alaska | Mean | — | 39.51 | 43.97 | — | — |
| %RSE | — | 5.80 | 1.80 | — | — | |
| Arizona | Mean | — | 37.32 | 35.57 | — | — |
| %RSE | — | 2.30 | 4.70 | — | — | |
| Arkansas | Mean | 27.26 | — | 29.29 | 33.88 | — |
| %RSE | 6.90 | — | 4.30 | 11.60 | — | |
| California | Mean | — | — | 54.06 | 43.26 | 63.53 |
| %RSE | — | — | 2.10 | 6.70 | 4.00 | |
| Colorado | Mean | — | 32.25 | 35.08 | 46.91 | 46.04 |
| %RSE | — | 5.30 | 2.30 | 4.00 | 4.20 | |
| Connecticut | Mean | — | — | 39.04 | 39.93 | 51.56 |
| %RSE | — | — | 0.80 | 5.00 | 5.70 | |
| Delaware | Mean | 28.98 | — | 38.06 | — | — |
| %RSE | 2.10 | — | 1.80 | — | — | |
| District of Columbia | Mean | — | 36.19 | 43.55 | 48.14 | 55.08 |
| %RSE | — | 3.20 | 1.70 | 1.60 | 4.40 | |
| Florida | Mean | 31.64 | — | 31.08 | — | — |
| %RSE | 5.30 | — | 1.90 | — | — | |
| Georgia | Mean | 31.40 | — | 32.97 | — | 42.69 |
| %RSE | 6.90 | — | 1.20 | — | 2.90 | |
| Hawaii | Mean | — | 43.73 | 47.51 | — | — |
| %RSE | — | 10.30 | 3.20 | — | — | |
| Idaho | Mean | — | 30.48 | 32.66 | 43.09 | 43.80 |
| %RSE | — | 4.40 | 1.70 | 3.70 | 6.70 | |
| Illinois | Mean | — | 36.92 | 35.48 | — | — |
| %RSE | — | 3.80 | 1.80 | — | — | |
| Indiana | Mean | — | 33.30 | 31.01 | — | — |
| %RSE | — | 3.60 | 1.70 | — | — | |
| Iowa | Mean | 28.49 | — | 28.44 | — | 31.52 |
| %RSE | 5.10 | — | 4.00 | — | 6.30 | |
| Kansas | Mean | 29.22 | — | 29.42 | — | 32.58 |
| %RSE | 5.60 | — | 4.60 | — | 5.20 | |
| Kentucky | Mean | — | 29.68 | 29.61 | — | — |
| %RSE | — | 5.60 | 1.50 | — | — | |
| Louisiana | Mean | 28.22 | 28.15 | 30.62 | 37.02 | — |
| %RSE | 6.60 | 4.30 | 4.20 | 11.40 | — | |
| Maine | Mean | — | — | 33.98 | — | — |
| %RSE | — | — | 2.50 | — | — | |
| Maryland | Mean | — | 34.97 | 35.56 | 44.28 | 46.82 |
| %RSE | — | 2.50 | 1.40 | 2.40 | 2.40 | |
| Massachusetts | Mean | — | — | 45.14 | — | — |
| %RSE | — | — | 0.80 | — | — | |
| Michigan | Mean | — | — | 34.33 | — | — |
| %RSE | — | — | 0.70 | — | — | |
| Minnesota | Mean | 31.66 | — | 39.56 | — | — |
| %RSE | 2.90 | — | 2.00 | — | — | |
| Mississippi | Mean | — | 27.03 | 27.93 | — | — |
| %RSE | — | 4.70 | 1.10 | — | — | |
| Missouri | Mean | 29.42 | — | 31.06 | — | 37.28 |
| %RSE | 5.40 | — | 5.30 | — | 4.80 | |
| Montana | Mean | — | 30.11 | 32.39 | 43.43 | 43.04 |
| %RSE | — | 4.20 | 1.70 | 4.30 | 8.40 | |
| Nebraska | Mean | 30.42 | 28.94 | 31.16 | — | 34.54 |
| %RSE | 4.30 | 15.40 | 4.00 | — | 3.70 | |
| Nevada | Mean | — | 37.01 | 39.66 | 50.89 | 46.45 |
| %RSE | — | 4.80 | 2.10 | 4.50 | 4.60 | |
| New Hampshire | Mean | — | — | 35.79 | — | — |
| %RSE | — | — | 0.90 | — | — | |
| New Jersey | Mean | — | — | 40.86 | 43.76 | 54.29 |
| %RSE | — | — | 1.70 | 7.90 | 3.80 | |
| New Mexico | Mean | — | 31.71 | 34.26 | 44.53 | 43.50 |
| %RSE | — | 4.90 | 2.20 | 3.80 | 4.90 | |
| New York | Mean | — | — | 41.59 | 41.36 | 52.93 |
| %RSE | — | — | 1.70 | 10.90 | 2.60 | |
| North Carolina | Mean | 32.04 | — | 30.39 | — | 41.80 |
| %RSE | 5.00 | — | 1.30 | — | 1.70 | |
| North Dakota | Mean | 31.00 | 29.55 | 31.79 | — | 34.44 |
| %RSE | 4.30 | 13.40 | 3.50 | — | 3.50 | |
| Ohio | Mean | — | — | 31.92 | — | 45.31 |
| %RSE | — | — | 0.80 | — | 8.30 | |
| Oklahoma | Mean | 28.03 | — | 30.34 | — | — |
| %RSE | 6.40 | — | 3.70 | — | — | |
| Oregon | Mean | — | 40.49 | 44.23 | — | — |
| %RSE | — | 6.40 | 1.80 | — | — | |
| Pennsylvania | Mean | — | 29.30 | 34.67 | 37.08 | — |
| %RSE | — | 3.00 | 1.10 | 9.70 | — | |
| Rhode Island | Mean | — | 32.94 | 38.17 | — | — |
| %RSE | — | 8.90 | 1.10 | — | — | |
| South Carolina | Mean | 32.07 | — | 30.20 | — | 44.19 |
| %RSE | 4.70 | — | 1.20 | — | 2.10 | |
| South Dakota | Mean | 28.11 | — | 27.81 | — | 30.86 |
| %RSE | 5.70 | — | 4.10 | — | 6.40 | |
| Tennessee | Mean | — | 27.91 | 28.95 | — | — |
| %RSE | — | 4.50 | 1.10 | — | — | |
| Texas | Mean | 28.81 | 30.09 | 33.23 | — | — |
| %RSE | 5.60 | 4.70 | 1.30 | — | — | |
| Utah | Mean | — | 29.92 | 31.87 | 43.06 | 43.25 |
| %RSE | — | 3.60 | 1.80 | 4.50 | 6.40 | |
| Vermont | Mean | — | — | 33.97 | — | — |
| %RSE | — | — | 2.60 | — | — | |
| Virginia | Mean | 32.26 | — | 32.15 | — | 44.64 |
| %RSE | 5.20 | — | 0.80 | — | 1.40 | |
| Washington | Mean | — | — | 39.14 | — | — |
| %RSE | — | — | 4.20 | — | — | |
| West Virginia | Mean | 31.26 | — | 29.07 | 37.71 | 41.06 |
| %RSE | 5.90 | — | 1.20 | 9.30 | 1.90 | |
| Wisconsin | Mean | — | — | 33.98 | — | — |
| %RSE | — | — | 0.50 | — | — | |
| Wyoming | Mean | — | 29.98 | 31.91 | 41.98 | 44.03 |
| %RSE | — | 3.90 | 1.70 | 4.00 | 7.80 | |
| Notes: Dash indicates data failed to meet publication criteria. %RSE = percent relative standard error. Source: “2018 modeled wage estimates,” National Compensation Survey (U.S. Bureau of Labor Statistics, August 2019), https://www.bls.gov/mwe/mwe-2018complete.xlsx. | ||||||
| Label | Characteristic name |
|---|---|
| 1 | Union |
| 2 | Nonunion |
| 3 | Time |
| 4 | Incentive |
| 5 | Full time |
| 6 | Part time |
| 7–21 | Full time, levels 1–15 |
| 22 | Full time, not able to be leveled |
| 23–37 | Part time, levels 1-15 |
| 38 | Part time, not able to be leveled |
| 39–53 | Levels 1–15 |
| 54 | Not able to be leveled |
| Source: U.S. Bureau of Label Statistics | |
Christopher J. Guciardo, "Estimating variances for modeled wage estimates," Monthly Labor Review, U.S. Bureau of Labor Statistics, March 2020, https://doi.org/10.21916/mlr.2020.3
1 Work levels are a ranking of the duties and responsibilities of employees within an occupation and enable comparisons of wages across occupations. Work levels are determined by the number of points given for specific aspects, or factors, of the work. For a complete description of point-factor leveling, see “National Compensation Survey: guide for evaluating your firm’s jobs and pay” (U.S. Bureau of Labor Statistics, May 2013), https://www.bls.gov/ncs/ocs/sp/ncbr0004.pdf.
2 Michael K. Lettau and Dee A. Zamora, “Wage estimates by job characteristic: NCS and OES program data,” Monthly Labor Review, August 2013, https://www.bls.gov/opub/mlr/2013/article/lettau-zamora.htm.
3 For a detailed description of the Taylor series variance estimation method, see Ralph S. Woodruff, “A simple method for approximating the variance of a complicated estimate,” Journal of the American Statistical Association, vol. 66, no. 334, June 1971, pp. 411–414, https://www.jstor.org/stable/2283947?seq=1#metadata_info_tab_contents.
4 For a detailed description of the Fay’s BRR variance estimation method, see David R. Judkins, “Fay’s method for variance estimation,” Journal of Official Statistics, vol. 6, no. 3, September 1990, pp. 223–239, https://www.scb.se/contentassets/ca21efb41fee47d293bbee5bf7be7fb3/fay39s-method-for-variance-estimation.pdf.
5 For a detailed description of the Occupational Employment Statistics procedures, see “Survey methods and reliability statement for the May 2018 Occupational Employment Statistics survey” (U.S. Bureau of Labor Statistics, March 2019), https://www.bls.gov/oes/2018/may/methods_statement.pdf.
6 For a detailed description of the National Compensation Survey procedures, see “National Compensation Survey measures: overview,” Handbook of Methods (U.S. Bureau of Labor Statistics, December 2017), https://www.bls.gov/opub/hom/ncs/home.htm.
7 Woodruff, “A simple method for approximating the variance of a complicated estimate.”
8 Judkins, “Fay’s method for variance estimation.”