An official website of the United States government
 United States Department of Labor
United States Department of Labor
This article summarizes recent research conducted by the U.S. Bureau of Labor Statistics to use alternative data sources and methods to improve price-change measurement for high-tech goods and services in the U.S. Consumer Price Index.
The U.S. Bureau of Labor Statistics (BLS) has a goal of transitioning a portion of the U.S. Consumer Price Index (CPI) market basket of goods and services from traditional data collection to nontraditional data sources and collection modes.[1] Using nontraditional data is not new to the CPI. BLS has used secondary-source data since the 1980s to develop sample frames, to serve in benchmarking analysis, and to supplement collected data to support hedonic modeling and sampling. However, outside of a few notable exceptions like postage, gasoline, used vehicles, and new vehicles, nontraditional data have not directly replaced traditional data collection for most of the CPI market basket. As nontraditional data sources improve and become more suitable for use in price index construction, BLS plans to pivot from using nontraditional data as a supplementary tool to using it as the very basis for CPI calculation, where it is deemed appropriate and cost effective to do so. As this transformation occurs, BLS must innovate the infrastructure it uses to calculate the CPI and reimagine several foundational principles, such as its current reliance on full-probability sampling as the basis of its data collection processes.
In this article, we review the background of, and issues with, calculating price indexes for televisions and wireless telephone services, particularly those issues related to quality change and quality adjustment; describe alternative data sources that we use in our research; and define our research methods.[2] Our research indexes are presented in the results section. We conclude with final observations and remarks.
In framing the motivation for pursuing nontraditional or new alternative data sources, researchers note several challenges that arise in calculating the CPI using traditional data collection methods, namely (1) the difficulty of maintaining constant quality price change for products and services in which product turnover is frequent, (2) the importance of incorporating new goods in a timely manner, and (3) the need to reduce sampling error.[3] The researchers highlight that new alternative data sources and methods provide BLS with an opportunity to address these challenges and may lead to more accurate measures of price change. Specific examples relevant to our research include (1) the use of secondary-source data to aid BLS data collectors in the selection of representative telecommunications samples and (2) the use of secondary-source data to assist in quality adjusting the prices of smartphones.
Research on the integration of nontraditional data into the CPI continues, and, in some cases, nontraditional data and new index methods have been adopted. For example, a 2020 paper by BLS economists provides a summary of innovations focused on high-tech products that experience rapid and complex quality change.[4] Specifically, the authors explored examples of smartphones and residential telecommunications services (landline telephone, internet, and cable and satellite television). For these product categories, secondary-source data were used to construct hedonic regression models that indirectly estimate quality-adjusted price changes whenever a unique item is replaced in the CPI survey. The authors also wrote about ongoing research into the use of alternative data and methods for other product categories such as wireless telephone services. The authors examined applications of hedonic methods in which indexes are calculated completely from model-estimated prices. The calculation of these hedonic indexes is more feasible with increased access to alternative data.
Recognizing the prospect of future modernization challenges, BLS commissioned the Committee on National Statistics (CNSTAT) of the National Academy of Sciences to convene a panel of price index experts. This panel provided guidance to BLS as it plans for and progresses through its transition to increased reliance on alternative data for calculating the CPI. The panel assessed new opportunities created by the availability of alternative data sources and released its findings in 2022.[5] Of particular interest for our analysis is recommendation 2.6, which encouraged BLS to research and assess the potential of alternative data sources for quality change adjustments. The panel suggested that initially this work could be part of an effort to replace price quotes from traditional data. However, the panel noted that the use of new alternative data would likely result in a need for new methods for adjusting for quality change. The panel also advised BLS to consider hedonic methods for products in which rapid quality changes are common, such as for high-tech items. Large datasets containing high-quality product specification information of high-tech items offer opportunities for improving price-change measurement, especially when used with hedonic methods.[6] The panel suggested that BLS explore creating indexes with the hedonic methods developed by Tim Erickson and Ariel Pakes in 2011.[7] These methods are novel because they can adjust for unobservable characteristics and can correct for sample selection effects. Finally, the panel advised BLS that implementation of the methodological improvements suggested in recommendation 2.6 could be consequential for high-expenditure items. In concluding its recommendation, the panel cited telecommunications goods and services as good examples of products to prioritize, an area in which BLS has already begun researching.
In 2021, a paper from a BLS researcher provided a systematic accounting of the impact of quality adjustments and other item replacement imputations on the U.S. CPI since 1999.[8] The researcher found that quality adjustments reduced the rate of CPI growth by 0.04 percent per year. The largest contributors to this trend were indexes with unambiguous, vertically differentiated product attributes.[9] However, he added that the hedonic adjustments used by BLS do not always have a clear relationship with hedonic theory.[10] In his conclusion, he stated that BLS has attempted to make improvements to address several well-known measurement issues stemming from the item replacement process. He also stated that several of the issues could be better addressed in other ways, outside the item replacement process. Specifically, he stated that the introduction of new goods need not be directly tied to the exit of another product as the current BLS method imposes. Rather, it may be more appropriate to apply methods for imputing prior-period prices for new goods or current-period prices for exiting goods outside of the traditional item replacement process.[11] Finally, he recommended that BLS explore methods for capturing changes in consumer welfare based on demand modeling. He added that the increased availability of transaction data and other nonsurvey data may aid BLS in this endeavor.
BLS has a long history of quality adjusting television prices through the traditional item replacement process. Since January 1999, hedonic regression models have been applied in the production of the CPI for televisions.[12] The impact of these adjustments was found to be rather small and the direction of the effects were mixed. The aforementioned 2021 paper found an annualized difference of −1.38 percent between the published index for televisions and a strict matched-model counterfactual index.[13] The counterfactual index fell faster than the official index, and the paper’s author stated that this difference could be due to unaccounted for quality change.[14] If the difference was caused by unaccounted for quality change, he suggests that BLS would be better off implementing a strict matched-model index for televisions rather than maintaining its current quality adjustment methods.
Compared with the index for televisions, the index for wireless telephone services has a much shorter history of being calculated with hedonic quality adjustments. Since 2017, BLS has used quality-adjusted prices at item replacement to calculate the CPI for wireless telephone services.[15] Hedonic adjustments have made large differences for item categories like telecommunication services, in which prices are stable within a product’s life cycle and quality improvements are introduced at the time of product turnover. For services like these, price changes outside of item replacements are rare.
Given the instructive comments from previous research, we evaluated how nontraditional data sources and methods could be used to improve how BLS handles quality change in televisions and wireless telephone services. Methodological advances in adjusting for quality change put forth by academia focus on demand-based modeling.[16] Demand-based modeling requires expenditure information that BLS does not currently collect in its survey data.[17] Moreover, as noted in appendix 2B of the CNSTAT report, statistical agencies do not use demand-based methods because a price index that relies on assumptions about consumer utility functions would not be reliable enough for official purposes.[18]
Another approach to measuring quality change uses hedonic regressions to predict prices. This approach interprets the hedonic coefficients as not being tied to any underlying consumer preferences and may not necessarily have an intuitive interpretation. In this approach, the primary purpose of a hedonic regression is to predict prices. As such, decisions about model specification are motivated by the predictive power of the regression.[19] The practice of using only predicted prices in the estimation of price indexes is referred to as the “full-imputation method.”[20] Recent innovations to the imputation method by Erickson and Pakes account for changes in unobserved characteristics.[21]
We believe that the hedonic imputation approach is the best option for incorporating alternative data into the calculation of the CPI, particularly for rapidly changing products. This approach allows for the introduction of new goods outside of the traditional item replacement process. We find further support for this view from other researchers, who state that for product areas with high turnover, the use of hedonic indexes is the most appropriate.[22] Prior research also show that the hedonic imputation approach is preferred over the time-dummy-hedonic approach if there is evidence of parameter instability over time. Prior to the availability of large nontraditional datasets, BLS did not have the data necessary to calculate hedonic indexes. In the next section, we will describe the data used in this article.
This section provides an overview of the data sources used in this article. We first discuss sources of product prices and characteristics data and then discuss the sources of consumer expenditure data used to derive weights.
For televisions, we use price and characteristics data collected through an API (application programming interface) of a national retailer of televisions (NRTV). Since October 2020, BLS has downloaded price and specification data from NRTV’s API three times per month.[23] On average, the NRTV televisions dataset contains approximately 400 unique television observations per month. In a typical month, about 90 percent of these observations are available to purchase either in-store or online. The remaining 10 percent of observations are listings for out-of-stock items. Our analysis indicates that NRTV employs a national pricing strategy, so geographic segmentation of the data is unnecessary.
Each month, we undertake a data-cleaning process on the televisions dataset. First, we delete observations that are not available for consumers to purchase. Next, we delete observations with certain trigger words in their description. For example, products that include the word “signage” in their item description tend to be light emitting diode (LED) signs purchased by businesses, not televisions purchased by consumers. Next, we delete observations with missing price data. Finally, for the remaining observations, we take the average price that has been collected throughout the month.[24] This final group of observations make up the dataset that is used to build our price-prediction model.[25]
We use data purchased from a market-research firm to estimate observation-level expenditure weights for the dataset described above. The vendor provides BLS with market segmentation information that is derived from surveys issued to American consumers. From October 2020 to December 2022, survey respondents reported an average of 16,400 television purchases per quarter, representing an average quarterly expenditure of $8.3 million. The vendor selects survey respondents to be demographically and geographically representative of the domestic population. Although consumers do not report specific universal product codes (UPCs) or stock-keeping unit (SKU) numbers, they do report product specifications like brand, screen size, and resolution. Survey respondents also report the outlet, location of purchase, and whether the purchase was made online or in-store. We calculated expenditure estimates with weighting data from the same period in which prices were collected.
Since surveyed consumers do not directly report model names, SKUs, or UPCs, there is no way to directly merge the expenditure data with NRTV’s pricing and specification data. Instead, expenditure weights must be estimated using an alternative process that links the expenditure data with NRTV data. To estimate expenditure weights for each observation, we use the expenditure data to segment the market by relevant specification variables. For televisions, we selected brand, resolution, and screen size because of their consistent statistical significance in regressions on price. NRTV expenditure totals are summed for each unique group of these three specification variables. For example, medium screen size, 4k resolution televisions sold by Brand Y may have accounted for $25,000 in expenditures among survey respondents during the last four quarters. These expenditure estimates are then merged into the NRTV dataset for each matched observation. We use a rolling four-quarter average to weight the data, where the most recent quarter includes the index reference month. Finally, to weight individual observations, we divide the total expenditure estimate in each brand/screen size/resolution group by the proportion of website reviews that an observation received during the past month. In a typical month, about 10 percent of observations do not receive a website review. These observations are given a weight of zero for that month.
For wireless telephone services, we use price and characteristics data purchased from a market research firm that specializes in the telecommunications industry. The vendor of these data uses both web-scraping and nonautomated methods of data collection to monitor and record service plan prices and characteristics offered to new customers by telecommunications providers. Although the vendor collects service plan data in nearly every media market in the country, we only purchase data from the markets that align with the CPI’s 75 sampling areas. The vendor collects data from nearly all telecommunications providers offering services within a designated market area (DMA). The service categories BLS purchases are landline telephone, internet access (residential and wireless), television (cable and satellite), bundled service packages of residential telephone, internet, and television, streaming video, premium channels, and wireless telephone. The focus of our article is wireless telephone services provided by mobile network operators. The service plans and their prices are available nationwide.
Each observation in the price and characteristics data is a unique service plan package.[26] The data provide relevant specification variables for each service plan. We derive an average monthly price for each service plan by factoring in promotional and standard monthly rates for the duration specified by the contract. We exclude charges for activation, and service fees and taxes are not provided. Almost every combination of provider and area in the CPI sample is also included in the alternative data source.
To derive weights for wireless telephone services, we use data purchased from a consumer research, data, and analytics firm. We receive these consumer survey data for wireless telephone services every other year. The data used in this article are aggregated responses to the household survey on wireless carriers covering the 2018 and 2019 survey periods. The vendor conducts ongoing annual studies of wireless carriers by surveying households regarding their wireless telephone ownership experiences.
We developed a process for summarizing the survey responses regarding the purchase and consumption of wireless telephone service plans into useful groupings. These groupings are based on the payment method (postpaid or prepaid), the number of lines serviced per plan, the amount of high-speed data included with the plan, and the type of service provider.[27] We then calculate plan-level shares of consumer-reported expenditure by the type of service provider. Next, we divide the total expenditure estimates in each payment group equally among the service plans that match the group's characteristics. For example, suppose postpaid plans with one serviced line and 50 gigabytes of data offered by Provider Y accounted for $20,000 in expenditures in the survey. If Provider Y offers two service plans that match those characteristics, we would allocate half of the total expenditure (i.e., $10,000) to each plan. Finally, we adjust the plan shares based on the provider’s national market share. The plan shares are used to weight individual service plans in the estimation of the hedonic regression models and in the weighting of the plan price relatives when calculating index relatives.
To construct an accurate cost of living index, statistical agencies must effectively adjust item-level indexes for quality change over time. Practitioners must look beyond traditional matched-model price indexes to capture quality change that results from product turnover. Current BLS methods for calculating television and wireless telephone service price indexes include applying hedonic price adjustments only when an item is replaced. In contrast, our research indexes are not reliant on item replacement to estimate quality change. Rather, all products are used to build a predictive regression on price, which serves as the foundation of index calculation. Thus, quality improvements introduced by new goods are immediately and fully integrated into our estimate of constant-quality price change.
In terms of relative importance, televisions account for nearly 0.14 percent of the CPI market basket while wireless telephone services represent 1.44 percent.[28] Currently, BLS calculates indexes for both items by using a traditional matched-model method with item replacement. In this method, BLS defines representative item categories, selects item samples, prices unique items over time, and when a unique item disappears, BLS replaces it with another item of similar quality. For certain item categories, BLS has used hedonic regression models for several decades to indirectly estimate quality-adjusted price changes when a unique item is replaced by an item of dissimilar quality. BLS began this practice in 1999 for televisions and for wireless telephone services in 2017. In cases where a quality-adjusted price change cannot be estimated, BLS uses class-mean imputation to impute current-period prices.[29] BLS calculates 32 elementary item-area indexes by a weighted geometric means formula and then takes a weighted arithmetic average over each area to obtain a national index for each item category.[30]
The hedonic imputation methods investigated for this article were motivated by the need to account for the effect of unobserved product characteristics in the price estimations of exiting products. Unobserved characteristics are features that improve product quality but cannot be measured (and thus cannot be included in a hedonic regression on price).[31] Failure to adjust for the effects of unobserved characteristics may lead to upward bias in an index because the quality change introduced by these features is not captured by a standard hedonic index. Erickson and Pakes propose that it is possible to predict the effect of unobserved product characteristics by using observable characteristics, thereby reducing the omitted-variable bias inherent in some hedonic regressions.[32] They propose a two-stage method. In the first stage, the natural logarithm of price (ln(price)) for both the current month (t) and previous month (t−1) is predicted by regressing observed characteristics on ln(price). In the second stage, the same set of observed characteristics, plus the month t−1 residual from the first-stage regression, is regressed on the change in first-stage residuals for continuing goods.[33] In our prediction of each observation’s month t ln(price), the observation’s predicted change in residual is added to its predicted period t ln(price). Like previous work, we extend this technique to entering goods and assume their t−1 residual is zero.[34]
This method is appropriate for many high-tech products like televisions. However, this method relies on the prices of continuing goods varying over time, and many telecommunications services have price changes primarily at the time of product turnover. Therefore, Erickson and Pakes’ two-stage approach is not recommended for wireless telephone services. Instead, a one-stage hedonic imputation index, as described by Pakes, is applied here to wireless telephone services.[35]
The general form of our log-level hedonic regression model can be specified as
![]()
where Zk is a vector of observable characteristics for product k. The function ht () is estimated with a weighted least squares regression. This hedonic equation varies over time and is estimated each period, allowing the function to detect changes in consumer valuations of goods and services. With this function, we can use hedonic imputation methods (namely, using observable characteristics to impute the missing prices for entering and exiting goods) to correct for quality change introduced by product turnover.
Because weighting data were available in the form of estimated expenditure share-weights, we used weighted regression functions. The effect of using expenditure-weighted hedonic regressions is that the items with the highest expenditure share (the most popular items) are emphasized. The weighted model more accurately maps the relationship between prices and characteristics for the mix of items purchased by consumers.
In our weighted least squares regression, prices are predicted for all goods in the current month (t) and previous month (t−1). For televisions, we apply the adjustment described in Erickson and Pakes’ 2011 paper to period t prices. Additionally, we extend the price predictions to exiting goods and entering goods. After we predict prices for time t and t−1, we calculate price relatives and then aggregate them into a national index by using a Törnqvist formula.[36] Since NRTV employs a national pricing scheme and there is no regional variation in the price of wireless telephone service plans, we calculate a single national index for each item with the following equation,
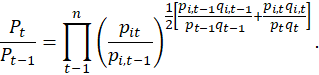
Our resulting hedonic indexes are derived completely from prices predicted by the hedonic regression models. In the literature, this process is referred to as “full imputation.” Practically, we use prices predicted by our hedonic regressions to calculate price relatives for continuing, entering, and exiting items. There are numerous advantages to full-imputation indexes.[37] We spotlight two of these advantages here. First, a change in the index is bound to the exact change in the cost of living under a weaker set of assumptions than those commonly seen in the literature.[38] Second, indexes other than full imputation are subject to a form of selection bias.[39] We integrate these insights into our choice of methods.
In this section, we present the hedonic imputation indexes calculated for televisions and wireless telephone services. These high-tech product groups are subject to periodic product changes, making them ideal for this kind of analysis. However, these groups are different in some respects, such as the presence of unobservable characteristics and the typical price change of a product during its life cycle. The differences between televisions and wireless telephone services, and the resulting differences in chosen price imputation methods, provide insight into the types of results we might see with other products with similar life-cycle effects. We also provide analysis of tests conducted to detect chain drift in our research indexes because chained, superlative index aggregation formulas, such as the Törnqvist method, are prone to this phenomenon.[40]
In chart 1 we compare multiple indexes: a one-stage, full-imputation hedonic index with the NRTV data, a two-stage, full-imputation hedonic index that incorporates an adjustment for unobserved characteristics with the NRTV data, and the official, nonseasonally adjusted CPI for televisions (rebased to 100 in January 2021). Both hedonic models use the same base model, which does not vary between periods. All three indexes reflect the same market trends.
All three indexes rose during the period when the international chip shortage increased production cost for manufacturers (January 2021–August 2021). As the chip market began to normalize, all three indexes began to decrease. This decrease was expected because rapid technological improvements provide a downward pressure on the index. The hedonic index may be more reactive to price shocks than the official CPI. Both hedonic indexes dropped in November 2021 and November 2022, when NRTV (and most similar retailers) began offering holiday sales on televisions. Both hedonic indexes also increased when holiday sales ended in January.
The official CPI for televisions was less reactive to 1-month price shocks. There are two possible reasons for this. First, the CPI component index contains prices from several retailers, while the NRTV indexes only represent a single retailer. NRTV may simply implement steeper holiday sales than the market at large. It is also possible that the NRTV indexes are more reactive because NRTV prices are collected at a much higher frequency than CPI prices. Since all televisions available to purchase were collected three times in November, it is much more likely that the NRTV data catches sales that may only last a few days. Most CPI observations are only collected every other month, giving each item much more time to go on sale and return from sale between collection dates.
Second, the two-stage hedonic index shows a more rapid price decline than the official CPI, but the one-stage hedonic index shows a slightly slower rate of price change in the long run. During the period of this study (January 2021–June 2023), the official CPI for televisions showed a 15.3-percent decrease, while the one-stage and two-stage hedonic imputation indexes showed 12.6- and 19.5-percent decreases, respectively. These results are expected and replicate the results of other research using hedonic imputation methods.[41] The one-stage hedonic index tracks quite closely to the CPI component index for televisions, while the two-stage hedonic index implies larger price declines. We find that the two-stage hedonic imputation index accounts for the falling residuals phenomenon described further in appendix A. Accounting for this phenomenon puts negative pressure on our estimation of price change. Since we have found, like Erickson and Pakes, that this phenomenon is at least partially driven by the exclusion of unobserved characteristics, we believe the two-stage method more accurately measures constant-quality price change in the market for televisions.
| Period | One-stage hedonic imputation model with Törnqvist weights | Two-stage hedonic imputation model with Törnqvist weights | Official CPI (Televisions) |
|---|---|---|---|
| January 2021 | 100.000 | 100.000 | 100.000 |
| February 2021 | 102.146 | 100.648 | 101.762 |
| March 2021 | 102.714 | 101.313 | 100.881 |
| April 2021 | 103.009 | 101.982 | 103.304 |
| May 2021 | 104.467 | 101.696 | 105.433 |
| June 2021 | 105.105 | 101.264 | 107.709 |
| July 2021 | 110.354 | 105.456 | 109.912 |
| August 2021 | 111.589 | 106.345 | 113.436 |
| September 2021 | 111.694 | 105.171 | 112.629 |
| October 2021 | 109.348 | 102.854 | 109.398 |
| November 2021 | 103.109 | 96.936 | 106.388 |
| December 2021 | 101.114 | 96.800 | 102.496 |
| January 2022 | 102.202 | 98.454 | 102.423 |
| February 2022 | 97.322 | 93.570 | 102.129 |
| March 2022 | 96.048 | 92.215 | 99.413 |
| April 2022 | 93.374 | 89.887 | 97.283 |
| May 2022 | 92.461 | 87.954 | 95.448 |
| June 2022 | 91.309 | 87.365 | 93.979 |
| July 2022 | 92.300 | 87.934 | 93.833 |
| August 2022 | 92.110 | 87.108 | 91.777 |
| September 2022 | 94.915 | 86.461 | 92.438 |
| October 2022 | 92.183 | 84.378 | 91.336 |
| November 2022 | 84.820 | 78.537 | 88.253 |
| December 2022 | 88.286 | 80.675 | 87.739 |
| January 2023 | 89.349 | 83.114 | 88.913 |
| February 2023 | 87.062 | 81.268 | 87.004 |
| March 2023 | 87.757 | 80.102 | 85.463 |
| April 2023 | 87.783 | 80.547 | 85.683 |
| May 2023 | 86.289 | 79.510 | 84.508 |
| June 2023 | 87.364 | 80.537 | 84.655 |
| Note: CPI = Consumer Price Index. Source: U.S. Bureau of Labor Statistics. | |||
In chart 2 we compare multiple indexes: a one-stage, full-imputation hedonic index calculated from alternative data, a two-stage, full-imputation hedonic index that incorporates an adjustment for unobserved characteristics calculated from alternative data, and the official, nonseasonally adjusted CPI for wireless telephone services (rebased to 100 in December 2018). We see some notable differences between these series over the analyzed period. For example, the one-stage hedonic imputation index fell 11.6 percent, the two-stage hedonic imputation index fell 3.1 percent, and the official CPI for wireless telephone services increased 4.8 percent. The differences between the official index and the research indexes were deepened by an increase in the official index in July 2020. In that month, about a third of the official CPI sample of price observations experienced item replacement and an accompanying price increase after prices were adjusted for quality changes. We attribute this index disparity to differences in sample composition and weighting and not to an inability of the hedonic indexes to correctly measure price change.
Compared with the one-stage hedonic index, the two-stage hedonic index resulted in only a modest decrease over the 4-year period. We saw the opposite result in our research with televisions. To understand this difference, we compare the two markets. In the televisions market, we observe discounted prices for older products. Quality change in this market is inherently captured in the price declines of older products that are being obsoleted by more technologically advanced entrants. Since televisions are a durable product, firms continue to sell older products at typically discounted prices until inventories are depleted. This pattern is not what we observe in the market for telecommunications services. Instead, new, higher quality products replace older, lower quality products, and both old and new products are not typically offered to new customers at the same time. The two-stage method relies on the observed price declines of obsoleted products. Without those declines, applying the adjustment leads to an index that shows little cost-of-living change. Therefore, we suggest that a one-stage hedonic imputation method is more appropriate for wireless telecommunications services.
| Period | One-stage hedonic imputation model with Törnqvist weights | Two-stage hedonic imputation model with Törnqvist weights | Official CPI (Wireless telephone services) |
|---|---|---|---|
| December 2018 | 100.000 | 100.000 | 100.000 |
| January 2019 | 100.486 | 100.239 | 99.852 |
| February 2019 | 100.853 | 100.239 | 99.710 |
| March 2019 | 101.300 | 100.684 | 99.587 |
| April 2019 | 99.903 | 99.611 | 99.770 |
| May 2019 | 98.822 | 98.413 | 99.712 |
| June 2019 | 99.204 | 98.535 | 99.837 |
| July 2019 | 99.049 | 98.456 | 99.779 |
| August 2019 | 96.774 | 98.441 | 99.643 |
| September 2019 | 96.117 | 98.058 | 99.544 |
| October 2019 | 96.645 | 98.361 | 99.495 |
| November 2019 | 95.439 | 98.336 | 99.684 |
| December 2019 | 94.241 | 98.336 | 99.738 |
| January 2020 | 94.242 | 98.336 | 99.721 |
| February 2020 | 94.029 | 98.336 | 99.501 |
| March 2020 | 94.264 | 98.510 | 99.486 |
| April 2020 | 93.078 | 98.700 | 99.583 |
| May 2020 | 92.647 | 98.591 | 99.654 |
| June 2020 | 93.318 | 99.566 | 99.544 |
| July 2020 | 91.600 | 99.219 | 103.165 |
| August 2020 | 91.640 | 98.860 | 103.954 |
| September 2020 | 89.634 | 98.342 | 104.117 |
| October 2020 | 92.744 | 98.342 | 104.068 |
| November 2020 | 91.802 | 98.132 | 103.907 |
| December 2020 | 91.323 | 98.132 | 103.808 |
| January 2021 | 91.373 | 98.132 | 103.821 |
| February 2021 | 91.572 | 98.132 | 103.819 |
| March 2021 | 88.038 | 98.132 | 103.473 |
| April 2021 | 88.029 | 98.132 | 103.389 |
| May 2021 | 88.302 | 98.132 | 103.415 |
| June 2021 | 88.384 | 98.125 | 103.471 |
| July 2021 | 88.835 | 98.125 | 103.290 |
| August 2021 | 88.195 | 95.443 | 103.103 |
| September 2021 | 89.283 | 96.258 | 103.533 |
| October 2021 | 90.507 | 97.734 | 103.529 |
| November 2021 | 90.487 | 97.712 | 103.529 |
| December 2021 | 90.011 | 97.711 | 103.449 |
| January 2022 | 90.431 | 97.711 | 103.307 |
| February 2022 | 90.784 | 97.712 | 103.402 |
| March 2022 | 90.515 | 97.712 | 102.673 |
| April 2022 | 89.299 | 96.179 | 102.706 |
| May 2022 | 88.637 | 96.179 | 102.691 |
| June 2022 | 88.504 | 96.175 | 102.557 |
| July 2022 | 88.504 | 96.175 | 102.540 |
| August 2022 | 87.084 | 96.176 | 102.491 |
| September 2022 | 87.822 | 96.176 | 102.405 |
| October 2022 | 87.818 | 96.170 | 102.115 |
| November 2022 | 87.096 | 95.508 | 104.530 |
| December 2022 | 88.372 | 96.850 | 104.762 |
| Note: CPI = Consumer Price Index. Source: U.S. Bureau of Labor Statistics. | |||
Törnqvist indexes can be subject to chain drift, which occurs when an index “indicates an overall price change, even though the prices and quantities in the current period have reverted to their levels of the base period.”[42] Chain drift often occurs in indexes built with scanner data because consumers tend to buy more of an item the month the item goes on sale.[43] This behavior will lead to a chained index that shows greater price declines than what a direct or multilateral index would show.[44] Life-cycle effects can lead to negative chain drift as well. Specifically, end-of-life runout sales are more heavily weighted in chained indexes than in multilateral indexes because multilateral indexes tend to reduce the impact of exiting goods.[45] Chain drift can also occur in the positive direction. Delayed changes in the purchasing behavior of consumers can lead to positive drift.[46]
To determine whether our chained hedonic Törnqvist indexes exhibit chain drift, we compare those indexes with Gini-Éltető-Köves-Szulc (GEKS) indexes calculated with the same predicted prices and quantities. For televisions, we use the one-stage hedonic Törnqvist index to measure drift. We compare the one-stage hedonic Törnqvist index against GEKS indexes with 25-month and 13-month windows. We run this test over a 25-month period so that the 25-month window GEKS index exhibits zero chain drift. The 13-month GEKS index employs mean splicing.[47] Our research index, the one-stage hedonic imputation Törnqvist, experienced a 25-month decrease of 16.88 percent compared with the 13-month and 25-month GEKS indexes, which fell 16.79 and 16.94 percent, respectively. Results are displayed in chart 3.
| Period | One-stage hedonic imputation model with Törnqvist weights | GEKS (13-month window) | GEKS (25-month window) |
|---|---|---|---|
| June 2021 | 100.000 | 100.000 | 100.000 |
| July 2021 | 104.993 | 105.116 | 105.091 |
| August 2021 | 106.169 | 106.531 | 106.504 |
| September 2021 | 106.269 | 106.628 | 106.537 |
| October 2021 | 104.037 | 104.389 | 104.218 |
| November 2021 | 98.101 | 98.409 | 98.132 |
| December 2021 | 96.202 | 96.434 | 96.229 |
| January 2022 | 97.238 | 97.494 | 97.443 |
| February 2022 | 92.595 | 92.880 | 92.754 |
| March 2022 | 91.383 | 91.655 | 91.538 |
| April 2022 | 88.839 | 89.219 | 88.930 |
| May 2022 | 87.970 | 88.277 | 88.094 |
| June 2022 | 86.874 | 87.243 | 87.051 |
| July 2022 | 87.816 | 88.177 | 87.990 |
| August 2022 | 87.636 | 87.924 | 87.685 |
| September 2022 | 90.305 | 90.459 | 90.351 |
| October 2022 | 87.705 | 87.959 | 87.771 |
| November 2022 | 80.700 | 80.925 | 80.682 |
| December 2022 | 83.998 | 83.881 | 83.753 |
| January 2023 | 85.009 | 84.958 | 84.809 |
| February 2023 | 82.834 | 83.013 | 82.856 |
| March 2023 | 83.495 | 83.611 | 83.450 |
| April 2023 | 83.519 | 83.551 | 83.381 |
| May 2023 | 82.098 | 82.161 | 81.923 |
| June 2023 | 83.121 | 83.214 | 83.056 |
| Note: CPI = Consumer Price Index; GEKS = Gini-Éltető-Köves-Szulc. Source: U.S. Bureau of Labor Statistics. | |||
For wireless telephone services, we also use the one-stage hedonic Törnqvist index to measure drift. We compare the one-stage hedonic Törnqvist index against GEKS indexes with 37-, 25-, and 13-month windows. Each GEKS index employs mean splicing. Results are displayed in chart 4.
| Month | One-stage hedonic imputation model with Törnqvist weights | GEKS (13-month window) | GEKS (25-month window) | GEKS (37-month window) |
|---|---|---|---|---|
| December 2018 | 100.000 | 100.000 | 100.000 | 100.000 |
| January 2019 | 100.486 | 100.481 | 100.508 | 100.544 |
| February 2019 | 100.853 | 100.824 | 100.729 | 100.640 |
| March 2019 | 101.300 | 101.271 | 101.219 | 101.197 |
| April 2019 | 99.903 | 99.830 | 99.723 | 99.711 |
| May 2019 | 98.822 | 98.754 | 98.604 | 98.518 |
| June 2019 | 99.204 | 99.138 | 99.019 | 98.974 |
| July 2019 | 99.049 | 98.990 | 98.870 | 98.812 |
| August 2019 | 96.774 | 96.719 | 96.541 | 96.476 |
| September 2019 | 96.117 | 96.066 | 95.867 | 95.768 |
| October 2019 | 96.645 | 96.596 | 96.453 | 96.433 |
| November 2019 | 95.439 | 95.246 | 95.111 | 95.039 |
| December 2019 | 94.241 | 93.983 | 93.872 | 93.796 |
| January 2020 | 94.242 | 94.004 | 93.873 | 93.797 |
| February 2020 | 94.029 | 93.755 | 93.646 | 93.598 |
| March 2020 | 94.264 | 94.038 | 93.923 | 93.894 |
| April 2020 | 93.078 | 92.733 | 92.640 | 92.693 |
| May 2020 | 92.647 | 92.239 | 92.074 | 92.041 |
| June 2020 | 93.318 | 93.077 | 92.890 | 92.760 |
| July 2020 | 91.600 | 91.346 | 91.165 | 91.057 |
| August 2020 | 91.640 | 91.214 | 91.074 | 91.228 |
| September 2020 | 89.634 | 89.412 | 89.245 | 89.328 |
| October 2020 | 92.744 | 91.961 | 91.976 | 92.127 |
| November 2020 | 91.802 | 91.240 | 91.172 | 91.324 |
| December 2020 | 91.323 | 90.749 | 90.701 | 90.841 |
| January 2021 | 91.373 | 90.797 | 90.727 | 90.886 |
| February 2021 | 91.572 | 90.979 | 90.911 | 91.071 |
| March 2021 | 88.038 | 88.035 | 88.149 | 88.177 |
| April 2021 | 88.029 | 87.972 | 88.140 | 88.168 |
| May 2021 | 88.302 | 88.176 | 88.374 | 88.403 |
| June 2021 | 88.384 | 88.210 | 88.451 | 88.485 |
| July 2021 | 88.835 | 88.661 | 88.952 | 89.001 |
| August 2021 | 88.195 | 88.220 | 88.463 | 88.525 |
| September 2021 | 89.283 | 89.330 | 89.447 | 89.515 |
| October 2021 | 90.507 | 90.617 | 90.807 | 90.843 |
| November 2021 | 90.487 | 90.586 | 90.787 | 90.821 |
| December 2021 | 90.011 | 90.115 | 90.312 | 90.324 |
| January 2022 | 90.431 | 90.513 | 90.710 | 90.768 |
| February 2022 | 90.784 | 90.831 | 91.007 | 91.056 |
| March 2022 | 90.515 | 90.588 | 90.811 | 90.866 |
| April 2022 | 89.299 | 89.446 | 89.665 | 89.701 |
| May 2022 | 88.637 | 88.870 | 89.122 | 89.120 |
| June 2022 | 88.504 | 88.729 | 89.004 | 88.995 |
| July 2022 | 88.504 | 88.717 | 88.993 | 88.997 |
| August 2022 | 87.084 | 87.412 | 87.809 | 87.854 |
| September 2022 | 87.822 | 88.060 | 88.469 | 88.484 |
| October 2022 | 87.818 | 88.052 | 88.469 | 88.481 |
| November 2022 | 87.096 | 87.296 | 87.683 | 87.683 |
| December 2022 | 88.372 | 88.590 | 88.961 | 88.977 |
| Note: CPI = Consumer Price Index; GEKS = Gini-Éltető-Köves-Szulc. Source: U.S. Bureau of Labor Statistics. | ||||
Little drift is exhibited by the chained hedonic indexes for either item. For televisions, we observe an annualized difference of only 0.03 percent between the chained Törnqvist and 25-month GEKS indexes. For wireless telephones services, we observe an annualized difference of only 0.15 percent between the chained Törnqvist and 37-month GEKS indexes. These differences are to be expected because our indexes use estimated expenditures, not actual expenditure amounts. NRTV expenditure estimates are made using third-party market data that represents the last four rolling quarters of expenditure. Wireless telephone service expenditure estimates are derived from a single, static year of survey data and revised every 2 years. These expenditure estimates do not react to sales on a month-to-month basis like scanner data do. Because we use predicted prices for all goods in all periods, we do not see a drift from end-of-cycle sales. In total, because predicted prices are less subject to transitory price volatility than actual prices are, and because our weighting scheme estimates relatively stable observation-level expenditures month-to-month, chained hedonic imputation Törnqvist and hedonic imputation GEKS indexes are similar for both televisions and wireless telephone services.[48]
The goal of this research is to practically demonstrate how BLS can harness alternative data to calculate hedonic indexes. We show that the data used in this research can support such an application. The CPI program has multiple options to implement the use of alternative data sources. The televisions data from NRTV could be incorporated with traditionally collected data from other retailers of televisions to calculate basic indexes, while the wireless telephone services data are sufficient to represent the entire item-level index.
In addition to the practical implications, we find that hedonic imputation methods combined with Törnqvist aggregation produce research series that tend to decrease faster than the official indexes for televisions and wireless telephone services. For televisions, the two-stage hedonic imputation method better captures the effects of unobserved characteristics and reacts more quickly to one-month price shocks than does the CPI component index. For wireless telephone service, using alternatively sourced data greatly increases the representativeness of the index and the one-stage hedonic imputation method results in improved measures of constant quality price change because it allows for the introduction of new goods outside of the traditional item replacement process. We demonstrate that a two-stage approach is suitable for televisions, a product in which older models are discounted as newer models appear in the market. We also show that the two-stage approach is not recommended for products like wireless telephone services where products are not typically discounted throughout their life cycle.
Given that our research indexes use a chained Törnqvist aggregation formula that can produce indexes that are subject to chain drift, we compare our research series to various GEKS indexes calculated using the same predicted prices and estimated quantities. We find little evidence of extreme drift in the chained hedonic indexes for either item and conclude that this is due to our weights and prices being relatively more stable than weights and prices observed from scanner data.
In appendix A, we consider how the life cycle of a product affects price changes of televisions. Product life-cycle effects must be considered when calculating a true cost of living index. Specifically, in the televisions market, the majority of products enter at the highest price point in their product life cycle, and as their time in the market increases, their price decreases. This phenomenon can be visualized in two ways. First, chart A-1 compares a weighted Dutot index, which simply tracks weighted average prices in the NRTV sample, to strict matched-model Törnqvist and Jevons indexes. These strict matched-model indexes use no imputation, no item replacement, nor quality adjustment; they simply match models across time. The chained Törnqvist index uses the weighting mechanism described in the "Data" section of this article to estimate product-level expenditures.
| Period | Törnqvist | Jevons | Weighted Dutot |
|---|---|---|---|
| January 2021 | 1.000 | 1.000 | 1.000 |
| February 2021 | 1.007 | 0.997 | 1.042 |
| March 2021 | 1.013 | 1.000 | 1.076 |
| April 2021 | 1.020 | 1.013 | 1.114 |
| May 2021 | 1.019 | 1.020 | 1.119 |
| June 2021 | 1.016 | 1.019 | 1.127 |
| July 2021 | 1.058 | 1.048 | 1.241 |
| August 2021 | 1.068 | 1.051 | 1.296 |
| September 2021 | 1.057 | 1.029 | 1.318 |
| October 2021 | 1.034 | 0.994 | 1.340 |
| November 2021 | 0.975 | 0.943 | 1.299 |
| December 2021 | 0.971 | 0.939 | 1.230 |
| January 2022 | 0.987 | 0.950 | 1.229 |
| February 2022 | 0.938 | 0.905 | 1.179 |
| March 2022 | 0.924 | 0.892 | 1.176 |
| April 2022 | 0.902 | 0.875 | 1.158 |
| May 2022 | 0.883 | 0.851 | 1.131 |
| June 2022 | 0.876 | 0.834 | 1.114 |
| July 2022 | 0.883 | 0.829 | 1.164 |
| August 2022 | 0.876 | 0.813 | 1.128 |
| September 2022 | 0.872 | 0.802 | 1.155 |
| October 2022 | 0.853 | 0.784 | 1.169 |
| November 2022 | 0.796 | 0.747 | 1.089 |
| December 2022 | 0.815 | 0.748 | 1.132 |
| January 2023 | 0.839 | 0.758 | 1.128 |
| February 2023 | 0.819 | 0.738 | 1.144 |
| March 2023 | 0.806 | 0.732 | 1.169 |
| Source: U.S. Bureau of Labor Statistics. | |||
While the Dutot index rose over the period, the Törnqvist and Jevons indexes fell precipitously. This difference is because average price increases in the televisions market tend to occur when a product enters the market. Previous research has found this to be true in the market for televisions.[49] Chart A-2 visualizes this phenomenon in a different way, comparing the weighted average price of all televisions with weighted average prices for each model year. Note that each model year only appears on the chart when at least 50 unique televisions are offered for sale by NRTV.
| Period | Model year 2019 | Model year 2020 | Model year 2021 | Model year 2022 | All |
|---|---|---|---|---|---|
| January 2021 | 435.08 | 621.68 | 1 | 1 | 479.33 |
| February 2021 | 357.73 | 621.28 | 1 | 1 | 499.60 |
| March 2021 | 342.20 | 640.82 | 1 | 1 | 515.70 |
| April 2021 | 325.31 | 663.94 | 1 | 1 | 534.07 |
| May 2021 | 320.24 | 642.77 | 957.94 | 1 | 536.60 |
| June 2021 | 314.32 | 620.66 | 970.40 | 1 | 540.42 |
| July 2021 | 327.46 | 662.23 | 962.83 | 1 | 595.04 |
| August 2021 | 366.60 | 653.91 | 921.54 | 1 | 621.17 |
| September 2021 | 342.90 | 645.50 | 874.67 | 1 | 631.60 |
| October 2021 | 356.96 | 631.70 | 834.67 | 1 | 642.10 |
| November 2021 | 357.67 | 626.96 | 749.06 | 1 | 622.76 |
| December 2021 | 358.66 | 507.45 | 709.95 | 1 | 589.70 |
| January 2022 | 352.93 | 570.28 | 705.68 | 1 | 589.04 |
| February 2022 | 345.21 | 493.54 | 688.49 | 1 | 565.10 |
| March 2022 | 328.40 | 464.75 | 688.15 | 1 | 563.58 |
| April 2022 | 306.09 | 438.78 | 696.57 | 1 | 555.17 |
| May 2022 | 253.86 | 409.18 | 691.90 | 1 | 542.30 |
| June 2022 | 304.98 | 377.01 | 656.54 | 1,067.58 | 533.95 |
| July 2022 | 300.93 | 383.97 | 705.86 | 813.05 | 557.76 |
| August 2022 | 310.75 | 381.86 | 617.58 | 823.37 | 540.67 |
| September 2022 | 313.64 | 424.93 | 685.73 | 704.10 | 553.78 |
| October 2022 | 320.84 | 393.78 | 636.48 | 759.90 | 560.55 |
| November 2022 | 303.51 | 382.12 | 588.84 | 668.93 | 521.86 |
| December 2022 | 313.50 | 442.18 | 575.41 | 668.32 | 542.78 |
| January 2023 | 310.84 | 440.07 | 584.85 | 652.80 | 540.73 |
| February 2023 | 320.43 | 398.68 | 596.96 | 667.54 | 548.31 |
| March 2023 | 317.10 | 392.68 | 575.39 | 718.54 | 560.39 |
| Note: 1 Not applicable. Source: U.S. Bureau of Labor Statistics. | |||||
Although prices within each model year tend to fall over time, particularly during the first 6 months after introduction, average prices remain stable as consumers shift their expenditures to higher priced, newly introduced model years. The interaction between falling prices within a model year and expenditure shifts to recently introduced, higher priced televisions keeps average prices for all televisions relatively stable.
Just like actual sales prices, predicted television prices also fall throughout their product life cycle. However, predicted prices tend to fall at a slower rate than actual prices. Additionally, residuals tend to fall for televisions during their life cycle: televisions tend to have positive residuals (higher actual prices than predicted prices) at the start of their life cycle, and negative residuals (lower actual prices than predicted prices) at the end of their life cycle. Chart A-3 shows the weighted average residual of a television at different stages of their product life cycle. Chart A-4 displays the mean residual on ln(price) segmented by model year for 5 selected months. Both charts display the falling residuals phenomenon.
| Months since entry | Weighted average residual |
|---|---|
| 1 | 0.050 |
| 6 | 0.022 |
| 12 | 0.003 |
| 18 | 0.000 |
| 22 | -0.052 |
| Source: U.S. Bureau of Labor Statistics. | |
| Model year | June 2021 | December 2022 | June 2022 | December 2022 | June 2023 |
|---|---|---|---|---|---|
| 2019 | -0.004 | 0.012 | 1 | 1 | 1 |
| 2020 | 0.032 | 0.021 | 0.003 | -0.022 | -0.053 |
| 2021 | 0.126 | 0.037 | 0.031 | -0.041 | -0.047 |
| 2022 | 1 | 1 | 0.264 | 0.063 | 0.003 |
| 2023 | 1 | 1 | 1 | 1 | 0.059 |
| Note: 1 Not applicable. Source: U.S. Bureau of Labor Statistics. | |||||
There are two possible explanations for this phenomenon. First, firms may be aware that they are marketing towards different consumer groups at the start and end of a product’s life cycle. At the beginning of the life cycle, a “price insensitive” group who desire cutting-edge features no matter the price may make up most consumers. At the end of the life cycle, a “price sensitive” group, who wait until prices fall before making a purchase, may make up the majority of consumers. Negative product-level price relatives may exist for a television throughout the duration of its product life cycle not only because it is being obsoleted by higher-tech entrants, but also because the television is marketed to a consumer group with a lower willingness to pay for cutting-edge features. This effect is known as intertemporal price discrimination and has been identified in the vehicles market in previous research.[50] Since predicted prices only fall if the value of a television’s bundle of characteristics falls, the difference between a television’s predicted and actual price may capture the markup firms put on early life-cycle televisions regardless of that television’s characteristics.
A second possible explanation is offered by Erickson and Pakes. They contend that residuals are falling for products because “unobserved characteristics” exist in the market for televisions. These unobserved characteristics improve the visual or audio quality of a television but are not able to be captured by product specifications, and thus cannot be controlled for in a hedonic regression model. Newly introduced televisions are more likely to contain unobserved characteristics that are novel to the market and increase the value of a television. As a television ages, these unobserved characteristics become more ubiquitous in the market. The television becomes obsoleted by newer model years, and the product’s residual falls.
To test whether unobservable characteristics play a role in the falling residual phenomenon, we calculated three one-stage, full-imputation Törnqvist indexes, each based on prices predicted with unique sets of regressors. The regression model that predicts prices for the first index, “S5,” contains only binary variables for three high-value brands, screen area, and screen-area squared. The "S10" index's price prediction model includes all variables from the "S5" model and adds five highly predictive technological binary variables. The price prediction model for the final index, “S17”, includes all variables from the "S10" model and adds four less predictive technological binary variables and three more binary variables for brand. In short, the “S5” and “S10” price prediction models exclude characteristics, which artificially increases the number of unobservable features. If the exclusion of unobservable characteristics biases our index upwards, then each full-imputation index calculated with more features will result in sharper price declines.
| Period | S17 | S10 | S5 |
|---|---|---|---|
| January 2021 | 100.000 | 100.000 | 100.000 |
| February 2021 | 100.794 | 100.735 | 103.123 |
| March 2021 | 101.291 | 101.259 | 107.298 |
| April 2021 | 101.698 | 101.702 | 108.439 |
| May 2021 | 101.620 | 103.082 | 107.607 |
| June 2021 | 101.866 | 104.290 | 111.397 |
| July 2021 | 107.806 | 111.386 | 120.105 |
| August 2021 | 109.172 | 113.194 | 120.849 |
| September 2021 | 109.143 | 113.597 | 125.873 |
| October 2021 | 107.202 | 111.959 | 126.436 |
| November 2021 | 101.361 | 105.984 | 120.983 |
| December 2021 | 99.964 | 104.655 | 116.142 |
| January 2022 | 101.244 | 105.808 | 115.727 |
| February 2022 | 95.884 | 100.587 | 112.202 |
| March 2022 | 94.253 | 99.413 | 110.125 |
| April 2022 | 91.298 | 96.113 | 106.101 |
| May 2022 | 90.666 | 95.778 | 105.651 |
| June 2022 | 89.264 | 94.044 | 104.940 |
| July 2022 | 90.413 | 95.272 | 106.911 |
| August 2022 | 90.291 | 95.402 | 104.646 |
| September 2022 | 93.131 | 98.624 | 108.810 |
| October 2022 | 90.538 | 95.901 | 107.527 |
| November 2022 | 83.458 | 88.229 | 99.970 |
| December 2022 | 87.026 | 91.814 | 103.475 |
| January 2023 | 88.230 | 93.064 | 101.982 |
| February 2023 | 85.975 | 91.521 | 103.145 |
| March 2023 | 86.605 | 91.776 | 107.314 |
| April 2023 | 86.500 | 92.417 | 104.227 |
| May 2023 | 85.191 | 90.420 | 103.919 |
| June 2023 | 85.521 | 90.477 | 104.016 |
| Note: S5 contains only binary variables for three high-value brands, screen area, and screen-area squared. S10 adds five highly predictive technological binary variables. S17 adds four less predictive technological binary variables and three more binary variables for brand. Source: U.S. Bureau of Labor Statistics. | |||
As chart A-5 shows, as we increase the number of relevant specifications in our price prediction model, we see greater price declines in the resulting indexes. This result shows that unobserved characteristics drive at least some of the residual-change phenomenon described in this section. In 2011, Erickson and Pakes ran a similar test and saw similar results.
As previously mentioned, Erickson and Pakes offer a solution to the impact of unobservable characteristics on the estimation of change to the cost of living. Since chart A-5 shows that the exclusion of unobserved characteristics causes an upwards bias in a one-stage hedonic index, implementing Erickson and Pakes’ second stage adjustment would help reduce this source of bias in a hedonic index for televisions.
In our methods section, we stated that Erickson and Pakes’ method is most appropriate for products undergoing rapid quality change with the entry of new goods, but we noted that this method relies on intertemporal variation in prices for continuing goods. Unlike many consumer-electronics devices, most telecommunications services do not change price during their life cycles and indexes for these items experience price movement primarily when products enter and exit the market. Therefore, we did not pursue the two-stage approach for wireless telephone services. Instead, we used a one-stage hedonic imputation index for wireless telephone services.
To provide objective evidence regarding the absence of intertemporal price change for wireless telephone services, Table A-1 compares the percent of price relatives used in the calculation of the research hedonic indexes for televisions and wireless telephone services by type of price change. Only a small percentage of wireless telephone service plans experienced price changes during their life cycle between January 2019 and December 2022. In contrast, the majority of television observations exhibit a change in price on a month-to-month basis. Altogether, 97.6 percent of wireless telephone service observations exhibit no 1-month price change, while only 34.7 percent of televisions exhibit no 1-month price change, as displayed in Table A-1.
| Type of price change | Televisions | Wireless telephone services |
|---|---|---|
| Positive | 24.3% | 0.8% |
| None | 34.7 | 97.6 |
| Negative | 41.0 | 1.6 |
| Note: Television data cover the 2021–23 period, and wireless telephone data cover the 2019–22 period. Source: U.S. Bureau of Labor Statistics. | ||
In appendix B, we provide additional information on the product groups analyzed in this study by giving a brief overview of the datasets and explanatory variables.
The price and characteristics dataset for the period of study (January 2021–June 2023) for televisions consists of 10,058 total, usable price observations. We consider an observation usable if it is not eliminated in the data-cleaning process and if it receives a nonzero expenditure estimation. In total, there are 831 eligible, unique SKUs in the dataset. The NRTV dataset is rich with characteristic variables, the most relevant of which are described in table B-1.
| Characteristic | Type of variable | Description |
|---|---|---|
| Screen area | Continuous | Screen area in square inches |
| Resolution | Categorical | Number of pixels |
| Refresh rate | Categorical | Times per second the TV displays a new image |
| OLED | Categorical | Organic light emitting diode (leads to clearer, brighter picture) |
| Brand | Categorical | Which brand the television is |
| Number of HMDI inputs | Continuous | High-Definition Multimedia Interface inputs (allow TVs to connect with external devices like laptops, gaming systems, and Blu-Ray players) |
| Number of digital optical audio inputs | Continuous | Number of inputs for external speakers |
| HDR | Categorical | High dynamic range: improved contrast and light sensitivity |
| Smart TV | Categorical | The TV has integrated internet connectivity |
| Quantum dot technology (QLED) | Categorical | Semiconductor particles that lead to more accurate colors and a larger color gamut |
| Screen depth | Continuous | How thin the television is |
| Local dimming | Categorical | The TV can backlight only bright parts of an image |
| Model year | Continuous | The year the TV was manufactured |
| Glare resistance | Categorical | Glare resistant coating for outside viewing |
| Note: NRTV = national retailer of televisions. Source: U.S. Bureau of Labor Statistics. | ||
We use data from the market research company to weight our observations. Over 150,000 surveys are returned each quarter, with an average of over 16,000 reported television purchases. Data from this firm cover 100 percent of CPI’s geographic areas.
As noted earlier, the market research company allows users to segment national expenditure by product characteristics. The full list of characteristics that are reported on the surveys include smart TV capability, refresh rate, resolution, brand, and screen area. As mentioned in our data section, we selected brand, resolution, and screen size because of their consistent statistical significance in regressions on price. Because the company also allows users to segment expenditures by geographical location and/or consumer demographics, it is possible to create unique expenditure weights at the area level.
The price and characteristics dataset for the period of study (January 2019–December 2022) for wireless telephone services consists of approximately 7,700 observations and were purchased by BLS from a market research firm. These data include service plans providing wireless talk, text, and data. Services plans can be either prepaid or postpaid accounts. We limit prepaid plans to observations with less than three phone lines per plan and we limit postpaid plans to observations with less than six phone lines per plan. Each observation is a unique combination of service plan name, provider, number of serviced lines per plan, type of customer, contract length, and reference month. Wireless service plans are sold at one price nationally so there is no need to consider geographic characteristics. We derive an average monthly price over the contract length. The following explanatory variables are available for inclusion in the regression models: plan provider, account type (prepaid or postpaid), number of serviced lines per plan, amount of included high-speed data, amount of included hot-spot data, type of video quality provided by the plan, and promotional features such as streaming-video subscriptions. The most important quality variables are the number of serviced lines and the amount of high-speed data included per plan. Some service plans do not include data, and we code these plans as basic plans. Other plans describe themselves as offering consumers unlimited data when what they offer are large, capped amounts of high-speed data. When the consumer uses their allotted amount of high-speed data, they may continue to use data, but they will be demoted to a slower network. We use the amount of the high-speed data cap in our models. Still other plans claim to offer unlimited data with no caps. These plans are often lower priced than other “unlimited” plans because the consumer is only given access to lower speed networks. We code these unlimited plans differently than plans that offer access to high-speed data.
The data used for weighting observations in the study come from surveys conducted in 2018 and 2019 by a market research firm and were purchased by BLS. The data consist of approximately 30,000 responses to each survey that have been summarized to the service provider, account type, number of serviced lines per plan, and amount of included high-speed data per plan level. The amount of included high-speed data per plan is a categorical variable with three values: no data included, greater than or equal to 1 gigabyte (GB) and less than 10 GB, and greater than or equal to 10 GB. We removed outliers before calculating the expenditure shares. We calculated the expenditure shares in two steps. The first step summarizes by provider, and the second step adjusts the provider shares by their national market share so that all the expenditure shares in the dataset sum to 100. An example row in the dataset may show that 5 percent of total monthly expenditure is on postpaid, two-line plans with 1–10 GBs of included data from wireless provider XYZ. We combine the weight data with the price and characteristics data by determining which expenditure share category each service plan maps to and then dividing the expenditure share of that category equally among all service plans mapped to that category. To illustrate this, if the expenditure share category we just described above with 5 percent of the weight has four service plans that map to it, each of those four plans will receive a final expenditure share of 1.25.
Appendix C provides a short overview of some of the estimation results of the hedonic models used in this research.
Our regression analyses were informed by machine learning feature selection techniques. We used the GLMSELECT procedure in SAS to suggest a parsimonious model for wireless telephone service. The GLMSELECT procedure uses a stepwise selection process informed by k-fold cross validation to specify a sparse model with high predictive power. In Python, we used LASSO (least absolute shrinkage and selection operator) and random forest techniques to suggest a highly predictive model for televisions. Feature selection techniques like these will be particularly useful if BLS adopts these data and methods for monthly index calculations. Automating the initial stages of the hedonic model estimation process would allow BLS to maintain a well-specified model within its monthly production schedule. Ultimately, we evaluated the models suggested by the machine learning tools for each item and adjusted the model specifications on the basis of economic knowledge and expertise of the respective markets and datasets.[51]
| Period | January 2021 | June 2023 |
|---|---|---|
| Dependent variable | ln(price) | ln(price) |
| Mean square error | 0.05417 | 0.1145 |
| R-Square | 0.9668 | 0.9355 |
| Number of observations | 288 | 394 |
| Variables | Parameter estimates | |
| Intercept | 4.81864 1 | 4.83660 1 |
| (0.12036) | (0.15378) | |
| Screen area (square inches) | 0.0051817 1 | 0.00038549 1 |
| (0.00008) | (0.00008) | |
| Screen area squared | 2.38568E-08 | 3.686463E-8 3 |
| (0.00000) | (0.00000) | |
| Depth (inches) | -0.07664 1 | -0.07522 1 |
| (0.02658) | (0.02343) | |
| Quantum dot technology | 0.39060 1 | 0.32852 1 |
| (0.03467) | (0.04035) | |
| OLED (organic light emitting diode) | 0.71663 1 | 0.65068 1 |
| (0.05369) | (0.04949) | |
| Resolution (8K) | 1.35033 1 | 1.18755 1 |
| (0.11150) | (0.14341) | |
| Resolution (4K) | 0.50554 1 | 0.48530 1 |
| (0.09759) | (0.14341) | |
| Resolution (full high definition 1080p) | 0.27660 1 | 0.28763 2 |
| (0.09281) | (0.13291) | |
| Refresh Rate (120 Hertz) | 0.42095 1 | 0.36381 1 |
| (0.03285) | (0.03730) | |
| Brand 1 | 0.59190 1 | 0.69580 1 |
| (0.03964) | (0.04965) | |
| Brand 2 | 0.22772 1 | 0.30918 1 |
| (0.03445) | (0.04965) | |
| Brand 3 | 0.21788 1 | 0.32825 1 |
| (0.04397) | (0.04860) | |
| 1 p < 0.001, 2 p < 0.005, 3 p < 0.010. Note: Standard errors in parentheses. Source: U.S. Bureau of Labor Statistics. | ||
| Period | Refresh rate (120 Hertz) | Resolution (4K) | Resolution (8K) | Resolution (full high definition 1080p) | OLED | Quantum dot technology | Brand 3 | Brand 2 | Brand 1 |
|---|---|---|---|---|---|---|---|---|---|
| January 2021 | 0.421 | 0.506 | 1.350 | 0.277 | 0.717 | 0.391 | 0.218 | 0.228 | 0.592 |
| February 2021 | 0.371 | 0.407 | 1.261 | 0.253 | 0.674 | 0.368 | 0.258 | 0.259 | 0.665 |
| March 2021 | 0.380 | 0.481 | 1.194 | 0.272 | 0.671 | 0.361 | 0.318 | 0.292 | 0.661 |
| April 2021 | 0.419 | 0.405 | 1.070 | 0.201 | 0.650 | 0.353 | 0.259 | 0.262 | 0.597 |
| May 2021 | 0.497 | 0.483 | 1.156 | 0.211 | 0.576 | 0.339 | 0.213 | 0.232 | 0.557 |
| June 2021 | 0.470 | 0.568 | 1.128 | 0.215 | 0.598 | 0.395 | 0.228 | 0.259 | 0.637 |
| July 2021 | 0.456 | 0.599 | 1.175 | 0.257 | 0.552 | 0.390 | 0.236 | 0.218 | 0.594 |
| August 2021 | 0.428 | 0.572 | 1.257 | 0.297 | 0.558 | 0.362 | 0.227 | 0.163 | 0.484 |
| September 2021 | 0.442 | 0.547 | 1.279 | 0.243 | 0.566 | 0.341 | 0.234 | 0.174 | 0.494 |
| October 2021 | 0.385 | 0.576 | 1.353 | 0.267 | 0.623 | 0.333 | 0.273 | 0.242 | 0.567 |
| November 2021 | 0.398 | 0.617 | 1.481 | 0.333 | 0.576 | 0.300 | 0.299 | 0.227 | 0.519 |
| December 2021 | 0.445 | 0.477 | 1.253 | 0.266 | 0.546 | 0.353 | 0.248 | 0.181 | 0.523 |
| January 2022 | 0.425 | 0.500 | 1.301 | 0.204 | 0.640 | 0.337 | 0.195 | 0.152 | 0.475 |
| February 2022 | 0.421 | 0.498 | 1.280 | 0.256 | 0.658 | 0.331 | 0.227 | 0.185 | 0.472 |
| March 2022 | 0.415 | 0.510 | 1.269 | 0.260 | 0.702 | 0.317 | 0.208 | 0.193 | 0.458 |
| April 2022 | 0.409 | 0.494 | 1.182 | 0.250 | 0.554 | 0.326 | 0.200 | 0.168 | 0.512 |
| May 2022 | 0.447 | 0.533 | 1.263 | 0.266 | 0.640 | 0.304 | 0.191 | 0.203 | 0.451 |
| June 2022 | 0.404 | 0.511 | 1.195 | 0.230 | 0.716 | 0.342 | 0.184 | 0.247 | 0.509 |
| July 2022 | 0.416 | 0.474 | 1.171 | 0.260 | 0.618 | 0.370 | 0.235 | 0.272 | 0.580 |
| August 2022 | 0.482 | 0.371 | 0.952 | 0.224 | 0.543 | 0.379 | 0.289 | 0.285 | 0.589 |
| September 2022 | 0.463 | 0.530 | 1.382 | 0.230 | 0.764 | 0.341 | 0.264 | 0.287 | 0.511 |
| October 2022 | 0.445 | 0.328 | 1.110 | 0.186 | 0.665 | 0.311 | 0.213 | 0.255 | 0.576 |
| November 2022 | 0.490 | 0.311 | 0.966 | 0.215 | 0.554 | 0.296 | 0.207 | 0.187 | 0.444 |
| December 2022 | 0.348 | 0.318 | 1.258 | 0.188 | 0.787 | 0.394 | 0.234 | 0.224 | 0.516 |
| January 2023 | 0.400 | 0.384 | 1.195 | 0.200 | 0.731 | 0.401 | 0.188 | 0.247 | 0.528 |
| February 2023 | 0.417 | 0.310 | 0.968 | 0.222 | 0.590 | 0.332 | 0.165 | 0.217 | 0.539 |
| March 2023 | 0.488 | 0.344 | 1.073 | 0.224 | 0.601 | 0.274 | 0.197 | 0.259 | 0.494 |
| April 2023 | 0.426 | 0.326 | 1.013 | 0.188 | 0.610 | 0.293 | 0.253 | 0.264 | 0.619 |
| May 2023 | 0.431 | 0.326 | 1.018 | 0.298 | 0.566 | 0.253 | 0.300 | 0.258 | 0.634 |
| June 2023 | 0.364 | 0.485 | 1.188 | 0.288 | 0.651 | 0.329 | 0.328 | 0.309 | 0.696 |
| Note: OLED = organic light emitting diode. Source: U.S. Bureau of Labor Statistics. | |||||||||
| Period | Screen area (square feet) | Screen area squared | Depth (inches) |
|---|---|---|---|
| January 2021 | 0.075 | 3.435E-06 | -0.077 |
| February 2021 | 0.083 | 2.242E-06 | -0.120 |
| March 2021 | 0.075 | 3.190E-06 | -0.087 |
| April 2021 | 0.094 | -3.366E-06 | -0.079 |
| May 2021 | 0.072 | 1.323E-06 | -0.070 |
| June 2021 | 0.048 | 7.128E-06 | -0.041 |
| July 2021 | 0.048 | 7.271E-06 | -0.064 |
| August 2021 | 0.053 | 5.998E-06 | -0.089 |
| September 2021 | 0.045 | 7.510E-06 | -0.072 |
| October 2021 | 0.035 | 1.086E-05 | -0.050 |
| November 2021 | 0.024 | 1.290E-05 | -0.046 |
| December 2021 | 0.053 | 5.592E-06 | -0.051 |
| January 2022 | 0.037 | 1.046E-05 | -0.063 |
| February 2022 | 0.041 | 9.328E-06 | -0.051 |
| March 2022 | 0.037 | 1.062E-05 | -0.052 |
| April 2022 | 0.051 | 6.205E-06 | -0.048 |
| May 2022 | 0.049 | 6.527E-06 | -0.058 |
| June 2022 | 0.043 | 9.035E-06 | -0.037 |
| July 2022 | 0.059 | 3.861E-06 | -0.061 |
| August 2022 | 0.079 | -1.126E-06 | -0.091 |
| September 2022 | 0.020 | 1.476E-05 | -0.046 |
| October 2022 | 0.075 | 5.019E-07 | -0.077 |
| November 2022 | 0.083 | -2.660E-06 | -0.136 |
| December 2022 | 0.047 | 7.948E-06 | -0.092 |
| January 2023 | 0.044 | 7.986E-06 | -0.086 |
| February 2023 | 0.085 | -3.375E-06 | -0.138 |
| March 2023 | 0.079 | -1.100E-06 | -0.109 |
| April 2023 | 0.083 | -1.534E-06 | -0.094 |
| May 2023 | 0.079 | -7.814E-07 | -0.143 |
| June 2023 | 0.056 | 5.309E-06 | -0.075 |
| Source: U.S. Bureau of Labor Statistics. | |||
| Period | Adjusted R squared | Mean squared error (MSE) |
|---|---|---|
| January 2021 | 0.965 | 0.054 |
| February 2021 | 0.961 | 0.048 |
| March 2021 | 0.958 | 0.061 |
| April 2021 | 0.959 | 0.045 |
| May 2021 | 0.958 | 0.050 |
| June 2021 | 0.960 | 0.049 |
| July 2021 | 0.962 | 0.047 |
| August 2021 | 0.964 | 0.045 |
| September 2021 | 0.971 | 0.039 |
| October 2021 | 0.969 | 0.043 |
| November 2021 | 0.962 | 0.050 |
| December 2021 | 0.956 | 0.054 |
| January 2022 | 0.963 | 0.049 |
| February 2022 | 0.959 | 0.045 |
| March 2022 | 0.955 | 0.038 |
| April 2022 | 0.961 | 0.041 |
| May 2022 | 0.955 | 0.054 |
| June 2022 | 0.956 | 0.059 |
| July 2022 | 0.957 | 0.050 |
| August 2022 | 0.966 | 0.041 |
| September 2022 | 0.956 | 0.058 |
| October 2022 | 0.963 | 0.053 |
| November 2022 | 0.961 | 0.072 |
| December 2022 | 0.946 | 0.071 |
| January 2023 | 0.955 | 0.069 |
| February 2023 | 0.965 | 0.054 |
| March 2023 | 0.961 | 0.067 |
| April 2023 | 0.952 | 0.069 |
| May 2023 | 0.937 | 0.094 |
| June 2023 | 0.934 | 0.115 |
| Source: U.S. Bureau of Labor Statistics. | ||
| Month | January 2019 | December 2022 |
|---|---|---|
| Dependent variable | ln(price) | ln(price) |
| Mean square error | 0.13929 | 0.159 |
| R-Square | 0.8961 | 0.8287 |
| Number of observations | 148 | 163 |
| Variables | Parameter Estimates | |
| Intercept | 3.67348 1 | 3.49332 1 |
| (0.04562) | (0.06547) | |
| Prepaid account | -0.48417 1 | -0.44788 1 |
| (0.04845) | (0.06082) | |
| Number of lines | 0.24354 1 | 0.23527 1 |
| (0.01236) | (0.01519) | |
| ln(amount of high-speed data) | 0.17946 1 | 0.19902 1 |
| (0.01335) | (0.02060) | |
| Unlimited data plan (low speed) | 0.53938 1 | 0.69523 1 |
| (0.06451) | (0.07166) | |
| Provider 2 | -0.30195 1 | -0.36265 1 |
| (0.05152) | (0.05768) | |
| 1 p < 0.001, 2 p < 0.005, 3 p < 0.010. Note: Standard errors in parentheses. Source: U.S. Bureau of Labor Statistics. | ||
| Month | Provider 2 | Prepaid account | Number of lines | ln(amount of high-speed data) | Unlimited data plan |
|---|---|---|---|---|---|
| January 2019 | -0.302 | -0.484 | 0.244 | 0.179 | 0.539 |
| February 2019 | -0.364 | -0.487 | 0.245 | 0.193 | 0.492 |
| March 2019 | -0.320 | -0.484 | 0.249 | 0.192 | 0.486 |
| April 2019 | -0.261 | -0.472 | 0.250 | 0.172 | 0.412 |
| May 2019 | -0.319 | -0.468 | 0.248 | 0.176 | 0.427 |
| June 2019 | -0.295 | -0.458 | 0.249 | 0.177 | 0.428 |
| July 2019 | -0.303 | -0.457 | 0.248 | 0.178 | 0.433 |
| August 2019 | -0.262 | -0.477 | 0.227 | 0.156 | 0.364 |
| September 2019 | -0.284 | -0.478 | 0.223 | 0.155 | 0.368 |
| October 2019 | -0.232 | -0.478 | 0.223 | 0.155 | 0.368 |
| November 2019 | -0.217 | -0.444 | 0.218 | 0.158 | 0.385 |
| December 2019 | -0.193 | -0.442 | 0.216 | 0.153 | 0.388 |
| January 2020 | -0.193 | -0.445 | 0.216 | 0.153 | 0.385 |
| February 2020 | -0.172 | -0.415 | 0.215 | 0.146 | 0.410 |
| March 2020 | -0.167 | -0.397 | 0.214 | 0.145 | 0.434 |
| April 2020 | -0.141 | -0.522 | 0.216 | 0.156 | 0.468 |
| May 2020 | -0.213 | -0.554 | 0.202 | 0.164 | 0.499 |
| June 2020 | -0.218 | -0.477 | 0.208 | 0.166 | 0.442 |
| July 2020 | -0.226 | -0.414 | 0.217 | 0.155 | 0.405 |
| August 2020 | -0.289 | -0.512 | 0.206 | 0.200 | 0.557 |
| September 2020 | -0.345 | -0.492 | 0.214 | 0.199 | 0.546 |
| October 2020 | -0.225 | -0.476 | 0.227 | 0.180 | 0.445 |
| November 2020 | -0.245 | -0.523 | 0.224 | 0.196 | 0.487 |
| December 2020 | -0.239 | -0.567 | 0.226 | 0.190 | 0.470 |
| January 2021 | -0.248 | -0.565 | 0.227 | 0.188 | 0.478 |
| February 2021 | -0.240 | -0.565 | 0.226 | 0.190 | 0.472 |
| March 2021 | -0.411 | -0.566 | 0.224 | 0.193 | 0.519 |
| April 2021 | -0.412 | -0.567 | 0.224 | 0.194 | 0.519 |
| May 2021 | -0.422 | -0.525 | 0.223 | 0.200 | 0.538 |
| June 2021 | -0.423 | -0.516 | 0.223 | 0.201 | 0.542 |
| July 2021 | -0.408 | -0.474 | 0.226 | 0.190 | 0.505 |
| August 2021 | -0.407 | -0.662 | 0.227 | 0.164 | 0.545 |
| September 2021 | -0.357 | -0.656 | 0.238 | 0.157 | 0.521 |
| October 2021 | -0.434 | -0.491 | 0.226 | 0.198 | 0.610 |
| November 2021 | -0.434 | -0.492 | 0.226 | 0.198 | 0.610 |
| December 2021 | -0.459 | -0.542 | 0.223 | 0.214 | 0.657 |
| January 2022 | -0.425 | -0.427 | 0.228 | 0.203 | 0.632 |
| February 2022 | -0.396 | -0.438 | 0.229 | 0.194 | 0.674 |
| March 2022 | -0.398 | -0.433 | 0.232 | 0.193 | 0.657 |
| April 2022 | -0.437 | -0.531 | 0.231 | 0.217 | 0.726 |
| May 2022 | -0.395 | -0.507 | 0.233 | 0.218 | 0.757 |
| June 2022 | -0.393 | -0.517 | 0.233 | 0.218 | 0.757 |
| July 2022 | -0.393 | -0.517 | 0.233 | 0.218 | 0.757 |
| August 2022 | -0.386 | -0.546 | 0.228 | 0.216 | 0.716 |
| September 2022 | -0.384 | -0.558 | 0.229 | 0.214 | 0.738 |
| October 2022 | -0.384 | -0.559 | 0.229 | 0.214 | 0.737 |
| November 2022 | -0.381 | -0.548 | 0.234 | 0.221 | 0.767 |
| December 2022 | -0.363 | -0.448 | 0.235 | 0.199 | 0.695 |
| Source: U.S. Bureau of Labor Statistics. | |||||
| Month | Adjusted R squared | Mean squared error (MSE) |
|---|---|---|
| January 2019 | 0.896 | 0.139 |
| February 2019 | 0.910 | 0.131 |
| March 2019 | 0.908 | 0.133 |
| April 2019 | 0.886 | 0.143 |
| May 2019 | 0.887 | 0.141 |
| June 2019 | 0.885 | 0.144 |
| July 2019 | 0.890 | 0.142 |
| August 2019 | 0.885 | 0.134 |
| September 2019 | 0.881 | 0.135 |
| October 2019 | 0.882 | 0.136 |
| November 2019 | 0.864 | 0.134 |
| December 2019 | 0.872 | 0.130 |
| January 2020 | 0.871 | 0.130 |
| February 2020 | 0.850 | 0.136 |
| March 2020 | 0.846 | 0.137 |
| April 2020 | 0.837 | 0.151 |
| May 2020 | 0.855 | 0.146 |
| June 2020 | 0.868 | 0.123 |
| July 2020 | 0.864 | 0.128 |
| August 2020 | 0.865 | 0.146 |
| September 2020 | 0.866 | 0.146 |
| October 2020 | 0.889 | 0.134 |
| November 2020 | 0.881 | 0.139 |
| December 2020 | 0.878 | 0.140 |
| January 2021 | 0.867 | 0.142 |
| February 2021 | 0.870 | 0.139 |
| March 2021 | 0.861 | 0.146 |
| April 2021 | 0.861 | 0.146 |
| May 2021 | 0.866 | 0.144 |
| June 2021 | 0.865 | 0.145 |
| July 2021 | 0.872 | 0.137 |
| August 2021 | 0.758 | 0.206 |
| September 2021 | 0.767 | 0.202 |
| October 2021 | 0.859 | 0.145 |
| November 2021 | 0.859 | 0.145 |
| December 2021 | 0.850 | 0.155 |
| January 2022 | 0.860 | 0.145 |
| February 2022 | 0.852 | 0.149 |
| March 2022 | 0.847 | 0.153 |
| April 2022 | 0.736 | 0.226 |
| May 2022 | 0.738 | 0.233 |
| June 2022 | 0.738 | 0.234 |
| July 2022 | 0.738 | 0.234 |
| August 2022 | 0.725 | 0.230 |
| September 2022 | 0.729 | 0.226 |
| October 2022 | 0.730 | 0.227 |
| November 2022 | 0.733 | 0.227 |
| December 2022 | 0.829 | 0.159 |
| Source: U.S. Bureau of Labor Statistics. | ||
Craig Brown, and Jeremy Smucker, "Alternative data sources for high-tech products in the CPI," Monthly Labor Review, U.S. Bureau of Labor Statistics, December 2024, https://doi.org/10.21916/mlr.2024.23
1 See U.S. Bureau of Labor Statistics Strategic Plan, FY 2020–2025, (U.S. Bureau of Labor Statistics, last modified January 6, 2020), https://www.bls.gov/bls/bls-strategic-plan-2020-25.htm; for a concise summary of traditional data collection, see Crystal G. Konny, Brendan K. Williams, and David M. Friedman, “Big data in the U.S. Consumer Price Index: experience and plans,” in Big Data for Twenty-First-Century Economic Statistics, eds. Katharine G. Abraham, Ron S. Jarmin, Brian C. Moyer, and Mathew D. Shapiro, NBER Studies in Income and Wealth, vol. 79, (Chicago: The University of Chicago Press, 2022) pp. 69–98, https://www.nber.org/books-and-chapters/big-data-twenty-first-century-economic-statistics/big-data-us-consumer-price-index-experiences-and-plans; for additional details and a description of current (i.e., traditional) data collection methods, see "Consumer Price Index: data sources,” Handbook of Methods (U.S. Bureau of Labor Statistics, last modified September 6, 2023), https://www.bls.gov/opub/hom/cpi/data.htm.
2 For more information on quality change and quality adjustment, see “Quality adjustment in the CPI,” Consumer Price Index (U.S. Bureau of Labor Statistics, last modified March 24, 2023), https://www.bls.gov/cpi/quality-adjustment/.
3 In “Big data in the U.S. Consumer Price Index,” Konny, Williams, and Friedman classify the Consumer Price Index’s (CPI) alternative data sources into three main categories: (1) corporate-supplied data from CPI survey respondents, (2) secondary-source data compiled by a third party and purchased by the U.S. Bureau of Labor Statistics (BLS), and (3) web-collected data, which are data collected by BLS using either web-scraping or application programming interfaces (APIs).
4 See Craig Brown, Steven Sawyer, and Deanna Bathgate, “A review of hedonic price adjustment techniques for products experiencing rapid and complex quality change” (U.S. Bureau of Labor Statistics, November 2020), https://www.bls.gov/advisory/tac/review-of-hedonic-price-adjustment-techniques-for-products-experiencing-rapid-and-complex-quality-change-11-20-2020.pdf.
5 See Modernizing the Consumer Prince Index for the 21st Century (Washington, D.C.: National Academies Press, 2022), https://doi.org/10.17226/26485.
6 See recommendation 2.6 in Modernizing the Consumer Prince Index for the 21st Century.
7 See Tim Erickson and Ariel Pakes, “An experimental component index for the CPI: from annual computer data to monthly data on other goods,” American Economic Review vol. 101, no. 5 (August 2011), pp. 1707–38, https://doi.org/10.1257/aer.101.5.1707; see also, recommendation 2.5 and appendix 2B in Modernizing the Consumer Prince Index for the 21st Century.
8 See Brendan K. Williams, “Twenty-one years of adjustments for quality change in the U.S. Consumer Price Index” (UNECE, The Ottawa Group on Price Indices, May 2021), https://unece.org/statistics/documents/2021/05/session-documents/twenty-one-years-adjustments-quality-change-us.
9 Vertically differentiated goods are ones such that the preference for or against each good is based on objective and measurable elements rather than differences in taste.
10 For more information on hedonic adjustment, see “Quality adjustment in the CPI,” Consumer Price Index (U.S. Bureau of Labor Statistics, March 24, 2023), https://www.bls.gov/cpi/quality-adjustment.
11 For a full description of the traditional data collection process in the CPI, see "Consumer Price Index: calculation," Handbook of Methods (U.S. Bureau of Labor Statistics, March 24, 2023), https://www.bls.gov/opub/hom/cpi/calculation.htm.
12 See Brent R. Moulton, Timothy J. LaFleur, and Karin E. Moses, “Research on improved quality adjustment in the CPI: the case of televisions” in Proceedings of the Fourth Meeting of the International Working Group on Price Indices, Washington D.C., April 22–24, 1998, ed. Walter Lane (U.S. Bureau of Labor Statistics, 1999), pp. 77–99, https://stats.unece.org/ottawagroup/download/f63.pdf.
13 In “Twenty-one years of adjustment for quality change,” Williams defines a “strict matched-model index” as one in which a product must be observed in t and t−1 periods to be included in the index. The qualifier “strict” is used because only same product-version price change is used. This contrasts with the published U.S. CPI, which compares the prices of different products at the time of item replacement.
14 The difference between the counterfactual index and the official index is shown as a price increase at item replacement (despite the best efforts of BLS to remove the bulk of quality change through the combination of current hedonic adjustment methods and analyst judgements).
15 BLS adopted a similar approach to hedonic adjustment for residential telecommunications services in January 2019. The CPI maintains separate indexes for internet, landline telephone, and television services, though bundled combinations of those services can be included in each of the three categories. Hedonic adjustments in these categories typically adjust for faster internet download speeds and the number of televisions channels included in a package.
16 See Stephen J. Redding and David E. Weinstein, “Measuring aggregate price indices with taste shocks: theory and evidence for CES preferences,” The Quarterly Journal of Economics vol. 135, no. 1 (February 2020), 503–60, https://doi.org/10.1093/qje/qjz031.
17 We do not estimate demand-based indexes for this article since alternative datasets for both items only provide observation-level price and specification data. Monthly expenditures must be estimated using lagged third-party survey data. These expenditure estimates are not reactive enough, on a real-time basis, to calculate an accurate demand-based index. Although a few datasets from alternative sources we have investigated come close to meeting the data requirements for demand-based modeling, we have yet to identify a robust, reliable source for this information.
18 See Modernizing the Consumer Prince Index for the 21st Century.
19 This is in contrast to models that seek to understand the causal relationship between variables. For more information on hedonic regressions, see Modernizing the Consumer Prince Index for the 21st Century.
20 See Ernst R. Berndt, The Practice of Econometrics: Classic and Contemporary (Addison-Wesley Publishing Company, 1991); see also Ariel Pakes “A reconsideration of hedonic price indexes with an application to PC’s” American Economic Review vol. 93, no. 5 (December 2003), 1578–96, https://doi.org/10.1257/000282803322655455.
21 See Erickson and Pakes, “An experimental component index for the CPI.”
22 This is partially because hedonic indexes include the data of unmatched new and old models. See Mick Silver and Saeed Heravi “The difference between hedonic imputation indexes and time dummy hedonic indexes,” Journal of Business & Economic Statistics vol. 25 (2007), pp. 239–46, https://doi.org/10.1198/073500106000000486
23 BLS collects item-specific datasets for televisions, computers, tablets, smartphones, video game systems, virtual reality headsets, cameras, camcorders, DVD and Blu Ray players, dishwashers, washers and dryers, refrigerators, cooktops, and microwaves. Price and characteristics data for televisions contains 96 specification variables per observation, a customer review count tally for each observation, a variable that indicates each item’s availability, a regular offer price for the item, and (if applicable) an offered sales price. Each unique observation contains its own stock-keeping unit (SKU) number.
24 To calculate this average, we take the unweighted geometric mean of every price for the item during the month.
25 Our method of calculating a single monthly price from multiple monthly prices replicates the method in Brendan Williams and Erick Sager, “A new vehicles transaction price index: offsetting the effects of price discrimination and product cycle bias with a year-over-year index,” Working Paper 514 (U.S. Bureau of Labor Statistics, May 2019), https://www.bls.gov/osmr/research-papers/2019/pdf/ec190040.pdf.
26 The variables include a plan’s price offered by a specific provider, through a particular sales channel, to a particular type of customer (new or continuing), for a specific contract term length, in a particular month. The vender also provides additional features and characteristics of each package.
27 We split providers into two groups: national operators or mobile virtual network operators (MVNOs). The large national wireless providers are sometimes referred to as mobile network operators (MNOs). These providers build and own their wireless networks. Other providers in the market are branded resellers of network capacity that they lease from MNOs. These types of providers are referred to as mobile virtual network operators.
28 Weights are for the CPI for All Urban Consumers as of December 2022 and based on U.S. city average using 2021 weights.
29 For more information on imputation, see “Imputation,” Consumer Price Index (U.S. Bureau of Labor Statistics, last modified May 15, 2024), https://www.bls.gov/opub/hom/cpi/calculation.htm#imputation.
30 See "Consumer Price Index,” Handbook of Methods.
31 Examples of unobserved characteristics for televisions include the audio quality, color accuracy, and the quality of the picture at various viewing angles
32 See Erickson and Pakes, “An experimental component index for the CPI.”
33 The change in first-stage residuals is calculated by finding the difference between month t and t−1 residuals generated by our first-stage price prediction at the observation level.
34 Entering goods are those that are available in the current period but not the previous period. This is in contrast to exiting goods, which were available in the previous period but not in the current period, and continuing goods, which are available in the previous and current periods. For more information on the technique of setting the t−1 residual to zero, see Gabriel Ehrlich, John C. Haltiwanger, Ron S. Jarmin, David Johnson, Ed Olivares, Luke W. Pardue, Mathew D. Shapiro, and Laura Zhao, “Quality adjustment at scale: hedonic versus exact demand-based prices indices,” Working Paper 31309 (National Bureau of Economic Research, June 2023), https://doi.org/10.3386/w31309.
35 See Pakes, “A reconsideration of hedonic price indexes with an application to PC’s.”
36 Estimating current-period and previous-period weights allows us to use a superlative aggregation formula like the Törnqvist.
37 See Ehrlich, Haltiwanger, Jarmin, Johnson, Olivares, Pardue, Shapiro, and Zhao, “Quality adjustment at scale.”
38 See Berndt, The Practice of Econometrics; and Pakes, “A reconsideration of hedonic price indexes with an application to PC’s.” In “Quality adjustment at scale,” Ehrlich et al. emphasize that the critical assumption is that consumers have preferences for the characteristics found in the goods, rather than preferences for the goods themselves.
39 This selection bias arises because those models treat the residuals for continuing, entering, and exiting goods in an asymmetric manner. See Berndt, The Practice of Econometrics; Pakes “A reconsideration of hedonic price indexes with an application to PC’s”; and Ehrlich et al., “Quality adjustment at scale.”
40 “Superlative” here is used in the literal sense. That is, “superlative indexes approximate to the second order the underlying cost-of-living index.” See Robert J. Hill, “Superlative index numbers: not all of them are super,” Journal of Econometrics vol. 130, no. 1 (January 2006), pp. 25-43, https://doi.org/10.1016/j.jeconom.2004.08.018.
41 See Erickson and Pakes, “An experimental component index for the CPI.”
42 Chain drift is not unique to Törnqvist indexes. All chained, superlative indexes can experience drift to some extent. For more information, see Ludwig von Auer, “The nature of chain drift: implications for scanner data price indices” (UNECE, The Ottawa Group on Price Indices, March 2019), https://stats.unece.org/ottawagroup/download/f538.pdf.
43 If consumers purchase a greater quantity of an item in the month it goes on sale, the weight given to the observation’s relative in the sale month will be greater than the weight given to the observation’s relative in the month when the item returns from the sale.
44 Jan de Haan, “Reducing drift in chained superlative price indexes for highly disaggregated data,” presented at the Economic Measurement Workshop, Centre for Applied Economic Research, University of New South Wales, https://www.researchgate.net/publication/229051374_Reducing_Drift_in_Chained_Superlative_Price_Indexes_for_Highly_Disaggregated_Data; see also Jan de Haan and Heymerik van der Grient, “Eliminating chain drift in price indexes based on scanner data,” Journal of Econometrics vol. 161, no. 1 (March 2011), 36–46, https://doi.org/10.1016/j.jeconom.2010.09.004.
45 Daniel Melser and Michael Webster, “Multilateral methods, substitution bias, and chain drift: some empirical comparisons,” Review of Income and Wealth vol. 67, no. 3 (September 2021), 759–85, https://doi.org/10.1111/roiw.12495.
46 Von Auer, “The nature of chain drift: implications for scanner data price indices.”
47 The mean-splicing method calculates an average index from all possible periods in a window.
48 For an explanation of why hedonic prices are less subject to transitory price volatility, see Ehrlich, Haltiwanger, Jarmin, Johnson, Olivares, Pardue, Shapiro, and Zhao, “Quality adjustment at scale.”
49 Jan de Haan and W. Erwin Diewert, “Quality change, hedonic regression and price index construction” (UNECE, The Ottawa Group on Price Indices, The Deutsche Bundesbank, February 13, 2017), https://www.bundesbank.de/resource/blob/635108/8c57b268050f67992fe7cc2a0388024c/mL/2017-05-10-ottawa-group-01-2-paper-data.pdf.
50 Ana Aizcorbe, Benjamin Bridgeman, and Jeremy Nalewaik, “Heterogeneous car buyers: a stylized fact,” Economic Letters vol. 109, no. 1 (October 2010), pp. 50–53, https://doi.org/10.1016/j.econlet.2010.08.003.
51 An example of our manual model adjustments is the exclusion of explanatory variables that were found to be collinear.