An official website of the United States government
 United States Department of Labor
United States Department of Labor
Each month, the International Price Program (IPP) at the Bureau of Labor Statistics (BLS) collects roughly 21,000 prices for a representative sample of goods traded by approximately 3,500 importers and exporters to and from the United States. The prices represent the market basket of imports and exports. The sample of import and export transaction prices is drawn from the complete universe of all items traded during a calendar year as measured by the Census Bureau. Sampling variability results whenever a sample is used rather than the complete universe.
As of 2019, variance publication is expanded to cover the majority of published import and export price indexes for merchandise trade sampled items. Variances are not calculated for locality of origin, locality of destination, and terms of trade price indexes covering goods, nor for services price indexes. Because services price indexes are largely composed of nonsampled alternative source data, variances for these indexes are not calculated.
The variance results by year measure the absolute median 1-, 3-, and 12-month percent changes for all published import and export indexes along with the median standard error for those estimates. In those cases where an index temporarily does not meet publication criteria, IPP will still publish variance estimates for the index provided the index was published for at least nine months during the year. Tables are broken out by classification system down to the 5-digit level of detail for the Bureau of Economic Analysis (BEA) End-Use Classification System, the 5-digit level of detail for the North American Industrial Classification System (NAICS), and the 4-digit index level of detail for the Harmonized Classification System.
The standard error, the square root of the estimated variance, is a common measure used to derive confidence intervals for percent changes in the import and export price indexes. Confidence intervals can be used to determine if an index change is significantly different from zero.
Take for example the median absolute 1-month percent change of 0.2 percent for All Commodities import prices, as seen in Table 1. The standard error for imports on a 1-month basis was 0.09. So, deriving a confidence interval plus or minus two standard errors from the point estimate, assuming a normal distribution, the true change would most likely be 0.2 percent plus or minus 0.18, or between 0.02 percent and 0.38 percent.
There are different types of errors introduced when calculating the estimates of average price changes for imports and exports published by the Bureau of Labor Statistics. There are two sources of error: sampling and nonsampling error. Sampling error, reported in the tables of this report, is the error resulting from drawing a sample of imported and exported items to and from the United States, rather than using the entire universe of trade.
Nonsampling error can take a number of different forms. One form is misspecification error, which takes place if the universe of data from which the sample is being drawn does not correctly measure the actual population. For import and export prices indexes, this type of error could result if there are mistakes in the trade dollar value statistics measured by the Census Bureau. A second type of nonsampling error is nonresponse error. Each month, a subset of the items sampled by the Bureau of Labor Statistics does not have prices reported. This type of error results if the respondents and nonrespondents do not represent a similar cross section of the total universe. Another form of nonsampling error can be introduced from misreported prices, a possibility regardless of whether deriving the indexes from a sample or from the complete universe of data.
One issue when deriving an estimate from a sample is the potential trade-off between variance and bias. Variance is a measure of how much the estimates derived from numerous samples differ from the true value of the estimate. Bias results if the expected value of the estimate is either higher or lower than the true value of what is being estimated. An estimate could have a high sampling variance and still be unbiased if the expected value of the estimate is equal to the true value. Likewise, an estimate may have small variation over numerous samples, yet be biased if the expected value of the estimate deviates from the true value.
The Bureau of Labor Statistics strives to minimize both sampling and nonsampling error as much as possible. Sampling error is reduced by maintaining as many prices as possible to support an index given resource and company burden constraints. Nonsampling error is reduced by subjecting the data to careful review using automated checks and a staff of professional economists, as well as by employing methods to estimate missing observations.
Trade into and out of the United States is highly regulated and therefore highly documented. This allows the IPP to sample from a fairly complete and detailed frame. U.S. Customs and Border Protection provides the sampling frame for import merchandise, while the export merchandise frame is created from a combination of data collected by the Canada Border Services Agency, for exports to Canada, and from the Census Bureau for exports to the rest of the world.
The import and export merchandise universes are divided into two panels each, with each product-based panel representing approximately half of the trade dollar value for its respective universe. One import and one export panel are sampled each year, resulting in a fully sampled universe every 2 years. Each panel is sampled using a 3-stage sample design. The first stage independently selects establishments within product-based sampling strata using systematic probability proportional to size, where the measure of size is the total trade dollar value for establishments within the sampling stratum. The second stage selects more highly detailed product categories, known as classification groups, within each establishment–stratum combination selected during the first stage using the technique of systematic probability proportional to size with replacement. The final stage of sampling, which results in a unique item to price, occurs in the field and is a random selection technique with the probability of selection proportionate to field-collected trade estimates.
IPP calculates its indexes using a modified Laspeyres formula. Rather than calculate indexes relative to a base period, the IPP indexes are calculated relative to the previous period and are theoretically chained to the reweight period. For this reason, IPP’s indexes can be considered chained Laspeyres indexes. Explicitly, the index formula for the modified chained Laspeyres is derived from the classic formula as follows:
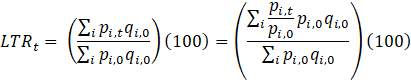
![]()
![]() ,
,
where
LTRt = the long term relative of a collection of items at time t;
pi,t = price of item i at time t;
qi,0 = quantity of item i in base period 0;
wi,0 = pi,0 qi,0, or the total revenue generated by item i in base period 0;
ri,t= pi,t / pi,0, or the long term relative of item i in period t; and
![]() , or the short term relative of a collection of items at time t.
, or the short term relative of a collection of items at time t.
Depending on the level of aggregation, the weights used during index aggregation are either trade dollar-based or probability-based. At the lowest level of aggregation, items are weighted by probability-based weights calculated monthly corresponding to detailed categories within establishments.
These weighted-item price relatives are combined across establishments and aggregated to the lowest level stratum indexes as
![]() ,
,
where
Ph,t= the price index for lowest level stratum h, at time t;
wk,t = the weight of detailed product category k, within stratum h;
wj,t = the weight of establishment j, within detailed product category k;
wi,t = the weight of item i, within establishment j and detailed product category k; and
![]() = the price relative of item i, from period t, to base period 0.
= the price relative of item i, from period t, to base period 0.
The weights used for these lowest level stratum indexes are derived from sampling frame trade dollar values, divided by the corresponding probabilities of selection determined by the sample design.
At the next level of aggregation, child strata-level indexes are aggregated to their corresponding parent stratum-level indexes. A child stratum index is simply one level of aggregation less than its parent stratum index. The weights used for this aggregation are based on Census Bureau trade dollar values for the base period.
The aggregation formula for these upper index levels is
![]() ,
,
where
PH,t = the price index at period t, for upper level index H;
wh,t = the weight at period t, for child index h; and
Ph,t = the price index at period t, for child index h.
A modified bootstrap method, applying rescaled sampling weights, is used to produce 150 replicate index set estimates from 150 simulated item set samples. Item set replicates are constructed according to IPP’s 3-stage sample design. At both of the first two stages of sampling, it is possible for a selection to be either a certainty selection (i.e. the probability of selection is greater than the iteratively calculated sampling interval) or a probability selection. The replicate resampling method takes this into consideration by first partitioning the selected items within each sampling stratum m into those items that resulted from certainty establishment selections and those items resulting from probability establishment selections. The item set resulting from establishment certainty selections is further partitioned into two item sets: sampling classification group certainty selections and sampling classification group probability selections. Thus, the set of all sampled items S is the union of these three partitions over all sampling stratum m;
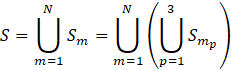 ,
,
where N is the number of sampling strata, ![]() , with p=1 for items selected from probability establishments, p=2 for items selected from probability sampling classification groups within certainty establishments, and p=3 for items selected from certainty sampling classification groups within certainty establishments.
, with p=1 for items selected from probability establishments, p=2 for items selected from probability sampling classification groups within certainty establishments, and p=3 for items selected from certainty sampling classification groups within certainty establishments.
Each bootstrap sampling, b, selects ![]() units within each partition of each sampling stratum as follows:
units within each partition of each sampling stratum as follows:
![]() ,
,
where ![]() is the number of units originally sampled in partition p of sampling stratum m.
is the number of units originally sampled in partition p of sampling stratum m.
Bootstrap item weights are then calculated as
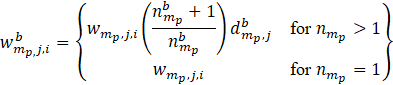 ,
,
where
= the bth replicate item weight for item i, within establishment j and sampling stratum partition mp;
![]() = the standard item weight for item i, within establishment j and sampling stratum partition mp; and
= the standard item weight for item i, within establishment j and sampling stratum partition mp; and
![]() = the number of times establishment j, within partition p of sampling stratum m, is selected in bootstrap sample b.
= the number of times establishment j, within partition p of sampling stratum m, is selected in bootstrap sample b.
In the rare instances that ![]() , a simple random sample of items within that establishment is selected. If only one item exists under this establishment singleton, that item is chosen with certainty.
, a simple random sample of items within that establishment is selected. If only one item exists under this establishment singleton, that item is chosen with certainty.
For each of the 150 bootstrap samples, chained indexes of the desired length are calculated at all levels of aggregation using these modified item weights, original probabilities of selection, trade dollar values, and collected price data. For variance estimates, the variance is calculated across replicate percent change values for all published indexes as ![]() where
where ![]() is the full sample estimate.
is the full sample estimate.
Tables 1 through 6 below present the absolute median percent change over the year for a given published index within the product and industry classifications used to publish official import and export price indexes, as well as the standard error of that estimate. Tables 1 and 2 present the BEA End-Use Classification System product categories, Tables 3 and 4 present the NAICS industry categories, and Tables 5 and 6 present the Harmonized Classification System product categories. The first column displays a text description of the category. The second column displays the code used to query the MXP Database. The subsequent columns record the absolute median percent change and standard error of the 1-month, 3-month, and 12-month price changes.
Last Modified Date: January 22, 2021