An official website of the United States government
 United States Department of Labor
United States Department of Labor
The following section explains how the Current Employment Statistics-State and Area (CES-SA) program produces employment, hours, and earnings. The CES-National (CES-N) program uses the same sample and collection methods, thus references to CES apply to both CES-N and CES-SA programs.
The Current Employment Statistics (CES) program uses a matched sample concept and weighted sample data to produce employment, hours, and earnings estimates. The methods are summarized in exhibit 1 and described in more detail below.
| Employment, hours, and earnings | Basic estimating cell (industry, 6-digit published level) | Aggregate industry level (super sector and, where stratified, industry) | Annual average data |
|---|---|---|---|
|
All employees |
All employee estimate for previous month multiplied by weighted ratio of all employees in current month to all employees in previous month, for sample establishments that reported for both months, plus net birth/death forecast. | Sum of all employee estimates for component cells. | Sum of monthly estimates divided by 12. |
|
Average weekly hours of all employees |
All employee hours divided by number of all employees. | Average, weighted by all employees, of the average weekly hours for component cells. | Annual total of aggregate hours (all employees multiplied by average weekly hours) divided by annual sum of all employees. |
|
Average hourly earnings of all employees |
All employee payroll divided by all employee hours. | Average, weighted by aggregate hours, of the average hourly earnings for component cells. | Annual total of aggregate payrolls (all employees multiplied by weekly hours and hourly earnings) divided by annual aggregate hours. |
|
Average weekly earnings of all employees |
Product of all employee average weekly hours and all employee average hourly earnings. | Product of all employee average weekly hours and all employee average hourly earnings. | Sum of monthly all employee aggregate payrolls divided by the sum of monthly all employees. |
|
Production and nonsupervisory employees |
All employee estimate for current month multiplied by weighted ratio of production and nonsupervisory employees to all employees in sample establishments for current month. | Sum of estimates of production and nonsupervisory employees for component cells. | Sum of monthly estimates divided by 12. |
|
Average weekly hours of production and nonsupervisory employees |
Production and nonsupervisory employee hours divided by number of production or nonsupervisory employees. | Average, weighted by production and nonsupervisory employment, of the average weekly hours for component cells. | Annual total of aggregate hours (production and nonsupervisory employment multiplied by average weekly hours) divided by annual sum of production and nonsupervisory employment. |
|
Average hourly earnings of production and nonsupervisory employees |
Total production and nonsupervisory employee payroll divided by total production and nonsupervisory employee hours. | Average, weighted by aggregate hours, of the average hourly earnings for component cells. | Annual total of aggregate payrolls (production and nonsupervisory employment multiplied by weekly hours and hourly earnings) divided by annual aggregate hours. |
|
Average weekly earnings of production and nonsupervisory employees |
Product of production and nonsupervisory employee average weekly hours and production and nonsupervisory employee average hourly earnings. | Product of production and nonsupervisory employee average weekly hours and production and nonsupervisory employee average hourly earnings. | Sum of monthly aggregate payrolls divided by the sum of monthly production employees. |
|
Source: U.S. Bureau of Labor Statistics. |
|||
Current Employment Statistics - State and Area (CES-SA) uses a cell stratification structure for each state and metropolitan area for which all employee (AE) estimates are provided. Cells within each geographic area are defined by ownership and North American Industry Classification System (NAICS) industry. They may range in detail from a high-level aggregate (e.g., goods-producing, private service-providing, or government) in small areas, to a more detailed 6-digit NAICS level, typically in statewide or larger metropolitan area estimates. Estimating cell structures may differ for production and nonsupervisory employees (PE), and hours and earnings for both AE and PE.
CES-SA uses a top-down estimation approach, where the sum of AE estimates, sometimes calculated at a detailed industry level, are constrained to values derived at an estimation super sector (ESS) level, usually defined at the 2-digit NAICS level. This allows for the publication of significant industry detail, while lessening the degree to which estimation error in cells with small sample sizes cumulate to total nonfarm. The list of potential basic ESS is provided in exhibit 2. In some states and areas, ESS listed in exhibit 2 may be combined to pool more sample for estimation purposes. Where the basic AE structure matches the ESS, separate ESS estimates may not be needed.
| Current Employment Statistics industry code | Major sector name | North American Industry Classification System codes included 1 |
|---|---|---|
|
10-000000 |
Mining and logging | 1133, 21 |
|
20-000000 |
Construction | 23 |
|
31-000000 |
Durable goods manufacturing | 33, 322 |
|
32-000000 |
Nondurable goods manufacturing | 31, 322 |
|
41-000000 |
Wholesale trade | 42 |
|
42-000000 |
Retail trade | 44–45 |
|
43-000000 |
Transportation, warehousing, and utilities | 22, 48–49 |
|
50-000000 |
Information | 51 |
|
55-000000 |
Financial activities | 52, 53 |
|
60-540000 |
Professional, scientific, and technical services | 54 |
|
60-550000 |
Management of companies and enterprises | 55 |
|
60-560000 |
Administrative and waste services | 56 |
|
65-610000 |
Educational services | 61 |
|
65-620000 |
Health care and social assistance | 62 |
|
70-710000 |
Arts, entertainment, and recreation | 71 |
|
70-720000 |
Accommodation and food services | 72 |
|
80-000000 |
Other services | 811, 812, 813 |
|
1 Only establishments with private ownership are used in each ESS 2 CES allocates 3-digit NAICS industries to this ESS based on industry description. Source: U.S. Bureau of Labor Statistics. |
||
State and local government is stratified into education and noneducation basic cells at the statewide level, except in the District of Columbia, Puerto Rico, and the U.S. Virgin Islands. Total federal government employment is a basic cell at the statewide level with the exception of three states, where it is stratified into more detailed basic cells. Total government is a basic cell in 43 metropolitan areas; total federal, state, and local government form basic cells in 325 areas, and 63 areas have other government basic structures (e.g., total federal, total state, local education, and local excluding education).
In addition to the basic estimation cells, CES-SA estimates some industry estimates independently; these series are not used for aggregating to the total nonfarm level, but may be combined with other independent estimates to form a summary estimate at an intermediate level.
Hours and earning series structures differ from structures for AE, generally providing less industry detail. All employees hours and earnings estimates are available at least at the goods-producing and private service-providing level in all 50 states and D.C., and at total private for Puerto Rico and all metropolitan areas. Hours and earnings of production employees in manufacturing is available for all states, D.C., Puerto Rico, the U.S. Virgin Islands, and 28 metropolitan areas. Additional hours and earnings detail varies by state and area.
A matched sample is defined to be all sample units that have reported data for the reference month and the month prior. Exhibit 3 shows all data that must be reported and matched for estimating each series type. Regardless of the data type being estimated, the respondent must provide AE for both months. The matched sample excludes any sample unit reporting that it is out-of-business and has zero employees. The section on birth–death model estimation more fully describes this aspect of the estimation methodology.
| Estimate | Reported data types |
|---|---|
|
All employees |
All employees |
|
Production and nonsupervisory employees |
All employees, production and nonsupervisory employees |
|
Average weekly hours of all employees |
All employees, total weekly hours of all employees |
|
Average hourly earnings of all employees |
All employees, total weekly hours of all employees, total weekly payroll of all employees |
|
Average weekly hours of production and nonsupervisory employees |
Production and nonsupervisory employees, total weekly hours of production and nonsupervisory employees |
|
Average hourly earnings of production and nonsupervisory employees |
Production and nonsupervisory employees, total weekly hours of production and nonsupervisory employees, total weekly payroll of production and nonsupervisory employees |
|
Source: U.S. Bureau of Labor Statistics. |
|
The robust weighted-link-relative estimator for AE series shown in equation 1 uses the relative change in the weighted matched sample of the estimating cell to move the previous month’s estimate forward to the current-month estimated level. A model-based component is applied to account for the net employment change resulting from business births and deaths not captured by the sample.
In some cases, a respondent’s microdata may be identified as an outlier and may receive a weight-reduction factor or be treated as atypical. This identification is generally performed by an automated procedure (described below). Atypical treatment allows CES-SA to use valid microdata to only represent the change in that particular establishment but not for changes in other establishments. In addition, strikes are treated as atypical, and other unique circumstances, such as damage to an individual establishment, may be treated as atypical as well.
Additional weight adjustments are used in certain cells where specific industries’ differential response rates are known to cause problems in estimates. Employment in religious organizations not subject to unemployment insurance (UI) laws is handled in a similar fashion to atypical employment.
The robust weighted link relative is used to estimate employment when adequate sample exists to directly estimate the relative over-the-month employment change in a given cell. A cell’s sample data is considered adequate for robust estimation when it passes disclosure tests and has either:
For some employment series, the sample is not adequate to use the robust weighted link relative. In these cases, a small area model is used in estimation, described in the section on special estimation methods. This model uses direct sample-based estimates of employment and variance, projections of historical (benchmarked) data, and the real-time relationship of these variables across domains to decrease volatility in estimation.
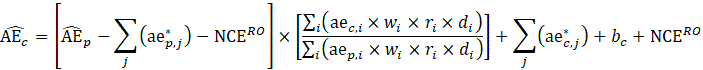
![]()
where,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The CES-SA matched sample sometimes contains a small number of reports that may have a large and adverse effect on the estimate. The influence of such reports may be because of large sample weights, a significant change in the reported employment levels, or a combination of these factors. If left untreated, influential reports may result in excessive volatility in the monthly estimates, especially at the most detailed publication levels.
The robust estimation procedure is designed to reduce the effect of the influential observations on the estimate of the relative over-the-month change. At the same time, it is recognized that the unusual and influential sample movements may represent similar behavior in the target population and a heavy intervention to the regular estimation procedure may lead to biased estimates. This is especially true if the sample is large. Therefore, the estimator is designed to reduce the volatility of the estimates that are due to extreme outlying reports while controlling the intervention to protect against the incurred bias.
The weighted link relative estimate is based on the ratio of weighted sums of 2 months of matched sample employment data. A scatterplot of the weighted employment reported in 2 consecutive months provides an insight on what units influence the estimate. Two examples are shown in figure 1: the survey weighted employment reported for the month (t) is plotted against the weighted employment reported for the previous month (t-1). The reference line represents the sample link relative, constructed in these examples so that the line has a slope of 1—markers on the line have constant employment.
An influential report would usually have a relatively large survey weight and/or a large change in its reported employment, and would show an unusual vertical residual from the reference line compared with other reports. Numerically, the influence of a report on the sample link relative estimate can be expressed in the form of weighted residuals.
![]()
where,
![]()
![]()
![]()
![]()
The influential reports are those having large positive or negative values of the weighted residuals compared with the other sample units. The extreme residuals are reduced to specific cut-off values. The cut-off values depend on the distribution of the weighted residuals in a given series and are determined independently for each month and industry series. Pushing the extreme residuals to the cut-off values is accomplished by using an appropriate weight adjustment factor.
The robust estimator addresses this problem by using a particular variation of a general method of weight reduction known as “Winsorization”.1 This process identifies influential reports at the UI level for each estimating cell.
The actual cut-off values are determined by examining the relative distances of units with extreme weighted residuals to the nearest but less extreme values in the same cell and month.
The first step consists of calculating the weighted residuals using equation 2. The weighted residuals from individual establishments are aggregated to the UI account level within each estimation cell. This is done because reports within a UI account may have similar reported change in employment. Since they are similar, it is possible that none of the individual reports will be identified as an outlying unit. At the same time, the UI level residual aggregated from all the responding establishments may be extreme and very different from other responding UI accounts in the cell.
The residuals may legitimately have very different values depending on the employment size class of the sampled UI accounts. To remove the effect of the size class, the residuals are “centered” within each size class, i.e., the average of the residuals within size classes is subtracted from each original residual.
The cut-off values are determined separately for the extreme positive and extreme negative residuals. The procedures are similar for the positive and negative residuals and are described here only for the positive residuals.
First, sort the residuals in each cell in descending order. Let ![]() denote the i-th largest centered positive residual:
denote the i-th largest centered positive residual:
![]()
Set the value F1 = d1 and F2 = 2d2 – d1.
The general formula for Fk is:
Fk = (k + 1)dk – (d1 + d2 +…+ dk ).
Proceed with the computations of the sequence of F1,…,Fk until, at some step k, Fk ≤ 0. Typically, this point is reached after only a few steps. Next, compute the cut-off value as the point between residuals dk and dk-1 as follows:
![]() ,
,
where,
![]()
The initial adjustments for units whose residuals are greater than L are
init.adji = L/di.
The cut-off values defined using the described procedure are always placed between some neighboring ordered residuals, so that all the residuals to the right of a cut-off value are greater than the cut-off value, although they may be very close to it. Based on the historical CES estimates, it has been found that the following rules for determining the final adjustments work the best.
An intervention, such as a weight adjustment, into the regular estimation procedure would reduce the variance of the estimate but it may introduce a bias. Therefore, the intervention, especially in samples of moderate to large sizes, is done with caution. For example, it is possible that there exist units in the non-sampled part of the population that are similar to the influential observations in the sample. Moderating the effect of the sample’s influential units may lead to a reduction in the representativeness of the sample. Since the nonsampled part of the population is not available, it is difficult to judge the amount and the need of intervention based only on the observed sample. One way to protect against unwarranted intervention is to verify its necessity using historical CES estimates. If the estimate falls within the historically observed bounds, then the intervention is deemed unnecessary and the weight adjustments are discarded.
At the very first step of the procedure, the sample link relative estimate is used when defining the residuals. This estimate may itself be affected by the extreme influential observations. Therefore, the whole procedure is performed a second time. The atypical units determined during the initial run are not used in calculating the adjustment factors during the second run.
The reports identified by the robust estimation techniques are treated as atypical in the link-relative technique, while all other matched sample responses are treated as typical in the link-relative technique.
The probability-based survey design, weighted link relative estimator, and net birth-death model (described below) account for the vast majority of employment change from business expansions, contractions, openings, and closings. Exceptionally large, known employment changes events are accounted for in CES-SA when they are not adequately captured in the matched sample and birth–death model.
The Bureau of Labor Statistics (BLS) works with state workforce agencies (SWA) to investigate publicly reported non-sample employment events, such as large business births, deaths, and strikes. This includes confirming the number of jobs affected and the event’s timing in relation to the CES reference period. If confirmed, estimates are adjusted by the portion of the event not captured by usual estimation procedures.
Non-response from certainty units that historically exhibit consistent, seasonal differences from the rest of the population—Quarterly Census of Employment and Wages (QCEW)—is accounted for through imputation in the matched sample. If an establishment reported CES data for the prior month (t-1) but not the current month (t), the matched sample uses the reported prior month CES data. Current month data is imputed by multiplying the reported prior month by the relative employment change in the prior year population data. If CES data was not reported in either the current or prior month, QCEW data is used to impute the level for both on the matched sample. To capture the seasonal movement of the noncovered employment portion for nonrespondents in education, prior year CES reported data is used for the imputation if available, otherwise QCEW data is also used. Since key nonrespondents are by definition different from the rest of the population, they are treated as atypical, and therefore only represent themselves in the estimates.
where,
![]()
![]()
![]()
![]()
Overall, adjustments to account for nonsample events and key nonrespondents largely offset at the statewide total nonfarm level over the course of a given year. However, these adjustments may bring estimates of monthly employment change at the detailed industry and metropolitan area level substantially closer to population values.
When a cell fails sample adequacy requirements, its direct sample-based estimates can experience high levels of relative variance. Though the cell’s robust sample-based employment estimate still approximately unbiased for the target population value, its high variance can disguise true over-the-month movements. In these cases, employment is estimated by using models that trade off some of the immediacy and geographic focus of purely probability-based estimates for improved estimate stability.
Beginning with the release of January 2022 estimates, CES-SA implemented its third-generation small area model for estimating employment in domains with insufficient sample for robust, sample-based estimation. The first generation of small area models was implemented in 2003; the second generation, based on the Fay-Herriot model, was introduced in 2009.2 The SAM Gen3 serves as a generalization of the Fay-Herriot model and loosens many of its assumptions.3
![]()
where,
![]()
![]()
![]()
![]()
![]()
![]()
Direct, sample-based estimates (![]() ) are regressed on the historical 5-year same-month employment trend (
) are regressed on the historical 5-year same-month employment trend (![]() ). A regression tree is run on the residuals from the linear regression
). A regression tree is run on the residuals from the linear regression ![]() to provide a set of groupings. These groupings, along with the
to provide a set of groupings. These groupings, along with the ![]() values, and potentially additional information, are included in the
values, and potentially additional information, are included in the ![]() matrix.
matrix.
The SAM Gen 3 co-models point estimates and their variances. The variance estimates used as a model input are derived using repeatedly grouped balanced half-samples (RGBHS) replication method on the current month matched sample. A structure similar to a generalized variance function (GVF) is used to describe the model for variances in SAM Gen3. For more information on the RGBHS and GVF, see the section on variance estimation.
The resulting model-based estimate can be presented as a weighted average of the direct ![]() estimate, state’s average estimate, and the regression-based (“synthetic”) part.
estimate, state’s average estimate, and the regression-based (“synthetic”) part.
![]()
where,
![]()
![]() ;
;
![]()
![]() = weighted state averages of
= weighted state averages of ![]() and
and ![]() ;
;
![]()
![]()
The model shrinks the estimate from the domain’s direct sample based ![]() toward respective state’s average and synthetic estimates. The amount of shrinkage depends on the variance of the direct estimate relative to variability of the other components.
toward respective state’s average and synthetic estimates. The amount of shrinkage depends on the variance of the direct estimate relative to variability of the other components.
The joint model is estimated using variational Bayes in Stan software. The estimation process includes an unsupervised clustering algorithm to detect structure in the data not defined by the groupings in the ![]() matrix and state random effects. Intercepts are derived for each domain based on their probability of being in each cluster.
matrix and state random effects. Intercepts are derived for each domain based on their probability of being in each cluster.
For all data types other than AE, CES-SA uses the robust weighted-difference-link-and-taper estimator applied to the matched sample. The difference link accounts for the over-the-month change in the sampled units, while the tapering feature keeps the estimates close to the overall sample average over time by using a composite base derived from the prior month’s estimate and matched sample average. The taper is considered a level correction because no benchmark source exists for non-AE data types. This estimator promotes continuity by heavily favoring the estimate for the previous month’s estimate (usually by 90 percent). Reported microdata may be identified as atypical, whereby the atypical microdata is subtracted before the base and matched samples, then added back to represent the individual establishment only.
CES-SA estimates a ratio of PE to AE (PER) using the weighted-difference-link-and-taper formula. The resulting ratio is then multiplied by the current month’s AE estimate to obtain a current estimate of PE.
![]()
where,
![]()
![]()
![]()
Variables used in equations 7 to 8 are defined below equation 9.
The CES-SA hours and earnings series are derived from reports of payrolls and the corresponding paid hours for all employees and for various types of production employees. Hours and earnings are for private-sector employees.
Estimates of average weekly hours (AWH), shown in equation 8, use a composite base of the prior month’s AWH estimate and sample ratio of total work hours-to-AE and apply the change in the sample average ratios to set the over-the-month change.
The estimator for average weekly hours for production and nonsupervisory employees takes the same form as average weekly hours for all employees, where AE and AWH represent estimates of PE and AWH for PE, respectively, and the matched sample totals ae and wh represent matched sample totals for production employees and weekly hours for production and nonsupervisory employees, respectively.
![]()
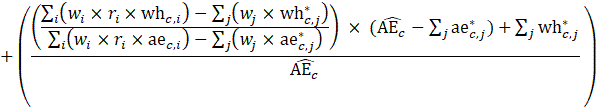
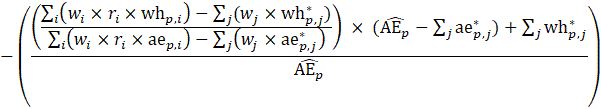
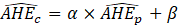
Estimates of average hourly earnings (AHE), shown in equation 9, use a composite base of the prior month’s AHE estimate and sample ratio of total weekly payroll-to-total weekly hours and apply the change in the sample average ratios to set the over-the-month change.
The estimator for average hourly earnings for production and nonsupervisory employees (PE-AHE) takes the same form as average hourly earnings for all employees (AE-AHE), where AE, AWH, and AHE represent estimates of PE and their hours and earnings, and the matched sample totals pr and wh represent matched sample totals of payroll and work hours for PE.
![]()
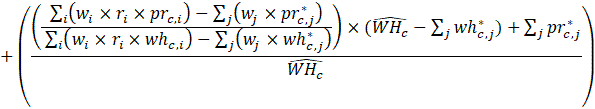
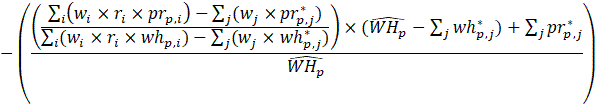
Listed below are the variable definitions for equations 7–9 where,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For all variables used in the equations above:
The process for selecting influential reports in non-AE estimates and adjusting their weights is closely related to the process for AE estimates, described in the section “Estimators for all employees,” and is used in estimating the number of production employees, as well as average weekly hours and average hourly earnings for both all employees and production employees.
The main difference between the AE and non-AE procedures lies in the measure of influence used. For AE estimates, the influence of a given respondent is considered to be the difference between prior month employment multiplied by the cell’s current sample link and current month reported employment, multiplied by the respondent’s selection weight. This approach is not appropriate for the weighted link and taper estimator used for non-AE. For non-AE, the influence is measured by recalculating the weighted link and taper estimate iteratively, removing each respondent one at a time. The difference between the estimate calculated with all respondents and the estimate calculated without a given respondent is considered to be that respondent’s influence.
![]()
where,
![]()
![]()
![]()
Beyond differences in influence functions, the non-AE weight adjustment algorithm diverges from the one used in AE in two ways. First, the adjustment factor used in selecting certainty units as atypical is 0.5 instead of 0.4. Second, the formula for calculating the cut-off point, from which adjustment factors are calculated, is closer to the second most influential positive and negative respondents: a is defined as 0.9F1/(0.9F1 – 0.1F2) instead of 0.8F1/(0.8F1 – 0.2F2). Both these modifications were chosen through empirical evaluation of simulated data.4
The CES sample alone is not sufficient for estimating the total employment level because each month new firms open for business, generating employment that cannot be captured by the sample. There is an unavoidable lag between a firm opening for business and its appearance on the CES sample frame, which is built from unemployment insurance (UI) quarterly tax records. Although these records cover nearly all U.S. employers and include business births, they only become available for updating the CES sampling frame 7 to 9 months after the reference month. After establishment births appear on the frame, additional time is required for sampling, enrolling, and collecting payroll data. In practice, CES cannot sample and begin to collect data from new firms until they are at least a year old.
There is a somewhat different issue in capturing employment loss from business deaths through monthly sample collection. Businesses that have closed are unlikely to respond to the survey, and data collectors may not be able to ascertain until after the monthly collection period that firms have in fact gone out of business. As with business births, confirmation of business deaths eventually becomes available from the lagged UI tax records.
Difficulty in capturing information from business birth and death units is not unique to the CES; virtually all current business surveys face these limitations. CES adjusts for these limitations explicitly, using a statistical modeling technique in conjunction with the sample for estimating employment for private-sector industries. Without the net birth-death model-based adjustment, the CES nonfarm payroll employment estimates would be considerably less accurate.
The CES-SA program separates the net birth-death methodology into two steps. The process applies only to nonfarm industries in the private sector.
The first step is to exclude from the sample employment losses from business deaths to offset a portion of employment gains from business births. Research and data have shown that employment increases from firm births roughly offset employment decreases from firm deaths in most months; therefore, step one accounts for most of the net employment change from business births and deaths.
To accomplish step one, CES-SA excludes reports with zero employment from the sample. Nonresponding sample units are automatically excluded from the matched sample, because they have no data for the reference month. These exclusions from the matched sample result in an over-the-month change that is based solely on employment from continuing businesses and effectively keep employment from business deaths in the estimates to represent employment from business births that occur after the sample was selected.
Step one accounts for most of the birth-death employment, but not all of it.
The second step is to model the net birth-death employment residual not accounted for in step one. The CES-SA program adjusts its sample-based estimates for the net birth-death employment missed by step one using autoregressive integrated moving average (ARIMA) modeling, an econometric technique often used to analyze and forecast time series. From the Quarterly Census of Employment and Wages (QCEW) universe employment series, each establishment is classified as a continuing, birth, or death unit. The process outlined in step one is applied to the QCEW data. Over-the-month changes are calculated from the continuing units, and deaths are used to impute for births. The differences between simulated estimates and actual employment totals measured by the QCEW each month are input into the ARIMA model to derive the net birth-death employment forecast.
The CES-SA program updates the net birth-death inputs to the ARIMA model each year for all statewide 3-digit NAICS industries as part of its annual benchmarking process. An additional 3 months of net birth-death data are appended to the input dataset as each new quarter of QCEW data becomes available.
The inputs to the ARIMA model depend on the age of the selected sample, which is selected in 1 year and rotated into production by industry sector and quarter over the following year. Quarterly sample rotation (see data sources section) results in differently aged samples by industry sector and has an inherent effect on birth-death values. To control for sample age, net birth-death forecasts are based on either 1 year out or 2 years out from selection. Exhibit 4 shows which sample is used to produce estimates for the first quarter of year t through the fourth quarter of year t. In the first quarter of year t, estimates for all industries are based on sample selected in year t-1, and all net birth-death forecasts are based on births and deaths in the first year after selection. In the second quarter of year t, sample selected in year t-1 is used for mining and logging; for trade, transportation, and utilities; and for financial activities; the net birth-death forecasts for these industries are based on input data 1 year after the sample was selected. All other industries are based on the prior sample year t-2 and require a forecast based on net birth-deaths in the second year after selection. In third quarter of year t, two additional industries—construction and leisure and hospitality—are rotated to the year t-1 sample and require a forecast for 1 year out, and the remaining industries on year t-2 samples require a forecast for 2 years out. This process repeats with more industries rotating in on the newer sample and requiring the 1-year out forecast until first quarter of year t+1 when all private-sector industries are based on year t-1 sample.
| Industry | Major industry | Second quarter, Yt | Third quarter, Yt | Fourth quarter, Yt | First quarter, Yt+1 |
|---|---|---|---|---|---|
|
Mining and logging |
10 | Year t-1 sample | Year t-1 sample | Year t-1 sample | Year t-1 sample |
|
Trade, transportation, and utilities |
40 | ||||
|
Financial activities |
55 | ||||
|
Construction |
20 | Year t-2 sample | |||
|
Leisure and hospitality |
70 | ||||
|
Information |
50 | Year t-2 sample | |||
|
Professional and business services |
60 | ||||
|
Other services |
80 | ||||
|
Manufacturing |
30 | Year t-2 sample | |||
|
Education and health services |
65 | ||||
|
Source: U.S. Bureau of Labor Statistics. |
|||||
For each statewide 3-digit NAICS industry, the most recent 6 years of employment data from the longitudinal database (LDB) is partitioned into five 25-month frames plus one half-frame. The additional half-frame is necessary in order to compile 13 months of data to derive 12 months of over-the-month changes.
| Frame | First month of span | Last month of span |
|---|---|---|
|
Frame 1 (half-frame) |
March year t-1 | March year t |
|
Frame 2 |
March year t-2 | March year t |
|
Frame 3 |
March year t-3 | March year t-1 |
|
Frame 4 |
March year t-4 | March year t-2 |
|
Frame 5 |
March year t-5 | March year t-3 |
|
Frame 6 |
March year t-6 | March year t-4 |
|
Source: U.S. Bureau of Labor Statistics. |
||
The birth-death residuals are calculated working with the frames and treating each microdata unit in the same way that the CES-SA treats microdata. Starting with the QCEW microdata for March t-6, microdata is separated into groups of continuous units, death units, and birth units for each reference month from April t-6 through March t-5 as follows:
Net birth-death value = population employment − (continuous employment + imputed employment)
The residual net birth-death values within the first and second halves of each frame are chained together to form separate time series (one comprised solely of first-half of each year of data, the other of second-half of each year of data).
Continuous samples deteriorate over time as firm deaths are not replenished by births. So, while the older samples continue to be used for some industries, the net birth-death inputs must be aged with the inputs identified in the second year after selection using the same process as the forecast for the 1-year-old sample, but aged 1 year.
Over-the-month changes of all net birth-death values are input into the forecasting model for the 1-year-old sample and the 2-year-old sample separately. The resulting forecasts are selected for use in estimation based on the age of the sample used for a given industry and quarter.
The difference between the cumulative state birth-death forecasts in a given month is raked to the forecasts derived at the national level by the CES-N program, as shown in equation 12. The difference is distributed to the state-level forecasts proportional to its employment level compared to other states.
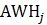
where,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Raking is done to ensure that birth-death forecasts are not a source of divergence between the sum-of-state and national employment data. In addition, national forecasts are updated each quarter with the availability of additional QCEW data, and raking is performed each quarter to make use of the updated national values.
After raking, birth-death factors are distributed to detailed industry levels and metropolitan areas proportional to their employment level. For example, if employment in NAICS 722 at the statewide level is 50,000, its raked forecast in month t is 700, and NAICS 722511 employment in a Metropolitan Statistical Areas (MSA) in the same state is 5,000, its raked forecast in month t is: ![]() .
.
For estimating cells comprising multiple industries, birth-death factors for the component industries are summed for use in estimation after the raking and distribution procedures.
CES-SA estimates are separated into five types of estimating cells: basic, summary independent, independent basic, and independent summary.
Aggregation starts at the most detailed industry-ownership level in each state and area, up to the 6-digit NAICS. All 6-digit industries that begin with the same 5 digits are aggregated to that 5-digit NAICS. All 5-digit industries that begin with the same 4 digits are then aggregated to that 4-digit industries. This process continues with all detailed industries falling into 1 of 17 major industry sectors, which are further aggregated into 10 supersectors, then goods-producing, private service-providing industries, and finally, to total private and total nonfarm. (See exhibit 5 and 6.) Total nonfarm represents the highest summary estimate for AE in all states and areas, while total private represents the highest possible summary estimate for all other data types.
| Current Employment Statistics industry code | Major sector name | North American Industry Classification System codes included and type of ownership |
|---|---|---|
|
10-000000 |
Mining and logging | 1133, 21 / Private |
|
20-000000 |
Construction | 23 / Private |
|
31-000000 |
Durable goods manufacturing | 33, 321 / Private |
|
32-000000 |
Nondurable goods manufacturing | 31, 321 / Private |
|
41-420000 |
Wholesale trade | 42 / Private |
|
42-000000 |
Retail trade | 44–45 / Private |
|
43-000000 |
Transportation and warehousing | 48–49 / Private |
|
44-220000 |
Utilities | 22 / Private |
|
50-000000 |
Information | 51 / Private |
|
55-000000 |
Financial activities | 52,53 / Private |
|
60-000000 |
Professional and business services | 54,55,56 / Private |
|
65-000000 |
Education and health services | 61,62 / Private |
|
70-000000 |
Leisure and hospitality | 71,72 / Private |
|
80-000000 |
Other services | 811,812,813 / Private |
|
90-910000 |
Federal government | All in-scope NAICS / Federal government |
|
90-920000 |
State government | All in-scope NAICS / State government |
|
90-930000 |
Local government | All in-scope NAICS / Local government |
|
1 CES allocates 3-digit NAICS industries to this major industry sector based on industry description. Source: U.S. Bureau of Labor Statistics. |
||
| Current Employment Statistics industry code | Aggregate Sector Name | Sectors included |
|---|---|---|
|
00-000000 |
Total nonfarm | 05-000000 Total private, 90-000000 Government |
|
05-000000 |
Total private | 06-000000 Goods-producing, 08-000000 Private service-providing |
|
06-000000 |
Goods-producing | 10-000000 Mining and logging, 20-000000 Construction, 30-000000 Manufacturing |
|
07-000000 |
Service-providing | 40-000000 Trade, transportation, and utilities, 50-000000 Information, 55-000000 Financial activities, 60-000000 Professional and business services, 65-000000 Education and health services, 70-000000 Leisure and hospitality, 80-000000 Other services, 90-000000 Government |
|
08-000000 |
Private service-providing | 40-000000 Trade, transportation, and utilities, 50-000000 Information, 55-000000 Financial activities, 60-000000 Professional and business services, 65-000000 Education and health services, 70-000000 Leisure and hospitality, 80-000000 Other services |
|
30-000000 |
Manufacturing | 31-000000 Durable goods, 32-000000 Nondurable goods |
|
40-000000 |
Trade, transportation, and utilities | 41-420000 Wholesale trade, 42-000000 Retail trade, 43-000000 Transportation and warehousing, 44-220000 Utilities |
|
90-000000 |
Government | 90-910000 Federal government, 90-920000 State government, 90-930000 Local government |
|
Source: U.S. Bureau of Labor Statistics. |
||
As noted in the section on stratification, CES-SA uses a top-down estimation approach where the sum of AE estimates are constrained to values derived from a parallel estimation super sector (ESS). After adjustments are made to AE data to control their summation to the ESS, AE data are re-aggregated for publication.
State and area structures may include series that represent summations of industries not found in NAICS—including total private; mining, logging, and construction; goods-producing; private service-providing; and government. These series may be basic or summary cells and are incorporated into the aggregation structure.
All employee (AE) and production and nonsupervisory employee (PE) data types use the same method for aggregation. Basic level estimates rounded to the hundreds are summed to the next higher summary-level estimate and then rounded according to the published precision. The process repeats at each level as data are aggregated to higher level summaries.
Average weekly hours are published in hours rounded to the tenths place, and rounded values are used in aggregation. Aggregate or summary levels of average weekly hours (AWH) are weighted by employment in component industries. Estimates of AWH at the basic levels are multiplied by employment estimates to calculate aggregate hours. Aggregate hours are summed for the basic industries and then divided by their summed employment. The process repeats at each level as data are aggregated to higher level summaries. The aggregation method for AWH of AE and PE is identical with the appropriate substitution of AE or PE employment and hours data in equation 13.
![]()
where,
![]()
![]()
![]()
Average hourly earnings and average weekly earnings are published in dollars rounded to the cent, and rounded values are used in aggregation. Estimates of average hourly earnings (AHE) at the basic level are multiplied by estimates of employment and by average weekly hours to calculate aggregate payroll, which is then summed to the next higher summary industry. The summed payroll data are then divided by the sum of aggregate hours (employment times average weekly hours) of all industries in the summary industry. The aggregation method of AHE for AE and PE is identical with the appropriate substitutions of AE or PE employment, hours, and earnings values in equation 14.
![]()
where,
![]()
![]()
![]()
![]()
Annually, the CES-SA benchmarks, or re-anchors, the sample-based employment estimates to the universe counts derived principally from the QCEW program. This benchmark process is done to account for statistical sampling and non-sampling errors (including response, nonresponse, and birth-death) that accumulate over the year. The QCEW counts provide a point-in-time census of payroll employment: they are not subject to sampling error and directly capture job growth from business births and deaths. However, the QCEW data are not as timely as the sample-based estimates and are subject to some forms of non-sampling error.
With each annual benchmark, the standard practice for state and area series is to revise 20 months of not seasonally adjusted data before the normal monthly estimation processes begin on the new levels. For example, with the development of the 2021 benchmark, levels were reestablished for the April 2020 through September 2021 reference months. UI tax reports are not collected on a timely enough basis to replace CES payroll estimates for the fourth quarter, October 2021 to December 2021. For this period, estimates are revised using the new September 2021 series level derived from the census employment counts. New sample-based estimates are developed from those levels that incorporate updated business birth/death factors and new or revised microdata.
A snapshot of the QCEW is the starting point for building the CES benchmark level. Employment that is covered under the CES definition, but not by state unemployment insurance (UI) tax laws is added to these levels. Approximately 97 percent of total nonfarm employment within the scope of the establishment survey is covered by UI. The remaining 3 percent, called noncovered employment (NCE), is present only in select industries, including employees such as railroad workers, insurance agents, student workers, and clergy. State workforce agencies (SWAs) are required to provide NCE counts to CES. SWAs mainly obtain NCE counts from the Railroad Retirement Board (RRB), the Surface Transportation Board (STB), and U.S. Census County Business Patterns, but some states conduct surveys and/or use other administrative data.
The total of the QCEW and noncovered employment (referred to as the population) replaces sample-based estimates for all state and metropolitan series. For benchmark year 2021, the employment levels for April 2020 through the September 2021 were replaced by these population counts. October and November 2021 re-estimates were generated as sample-based estimates linked from the new September 2021 levels. The links used for re-estimates may differ slightly from those used to derive preliminary estimates, because they include data from respondents who reported too late for inclusion in the previously published estimates, updated microdata, as well as new birth-death factors and model inputs. Figure 2 illustrates the timing of the benchmark replacement period and re-estimates for a given benchmark year y.
| Figure 2. Illustration of benchmark replacement period | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Year y-1 | |||||||||||
| Replacement period | |||||||||||
| JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| Year y | |||||||||||
| Replacement period | Re-estimates | ||||||||||
| JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| Source: U.S. Bureau of Labor Statistics. | |||||||||||
The first 6 months of each benchmark replace the last 6 months of the prior benchmark’s population counts. The next 3 months replace the prior benchmark’s re-estimates, while the remaining 9 months replace sample-based estimates linked from the last benchmark. Those first 6 months are updated with more recent versions of the QCEW and new noncovered employment counts. For the 2021 benchmark (April 2020 through September 2021), estimates are replaced once as part of the 2021 benchmark process. The April 2021 through September 2021 employment data are replaced again a year later as part of the 2022 benchmark process.
In the process of replacing the employment estimates, CES evaluates known administrative issues in the QCEW. The presence of noneconomic code changes (NECCs) is one such issue. Each year approximately one-third of all establishments in the QCEW are contacted as part of the Annual Refiling Survey (ARS). State workforce agencies contact companies and ask them to verify their North American Industry Classification System (NAICS) industry classification, location, and ownership. Ownership can be private industry; or federal, state, or local government. Based on ARS responses, updates are made to the QCEW data with first-quarter data. These administrative changes are referred to as NECCs. The effect of changes that represent less than 6 percent of the employment in a series is distributed across 12 months. This distribution is called a wedge.
![]()
where,
![]()
![]()
![]()
For a positive net NECC, employment is gradually added into the benchmark series from April through December, but subtracted in January and February, since the code change is implemented in the first quarter. The reverse is true for a negative net NECC. March reflects the full effect of the NECC.
For changes of 6 percent or more, CES staff lengthens the number of months across which the employment change is distributed. This requires editing historical data, which for benchmark year 2021 would be months prior to April 2020. In some cases, the time series is reconstructed using historical QCEW data instead of a wedge. If an establishment has a large NECC, CES staff can add its historical employment values to the series it should have been in all along, throughout the series history. This employment is then be subtracted from the series it should not have been in, again throughout series history. This in effect is a correction to historical data for an error in coding (industry, geographic area, and ownership), and makes the history more accurate.
Wedges are also used to address series breaks in the presence of other noneconomic changes in the QCEW data, for example a company improving their reporting detail from a statewide aggregate to individual worksite levels. Noneconomic changes in noncovered employment values, such as new calculation methods and changes based on noisy source data, are also wedged back in history.
Another type of adjustment is applied to most local government series which have an educational component. CES treats faculty that are not paid during the summer months as employed, which is not the case in the QCEW. Large drops in reported faculty during the summer months are added back to CES microdata values. To bring the benchmarked series in line with CES definitions of faculty employment, the monthly sample-based estimates of employment change are used to fill in benchmark employment for June through August.
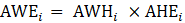
where,
![]()
![]()
![]()
Following the revision of employment estimates, estimates for production and nonsupervisory employees are recomputed using the revised all-employee estimates and the previously computed sample ratios of these workers to all employees.
Noncovered employment results from a difference in scope between the CES-SA program and the QCEW program, whose employment counts are derived from UI tax reports filed by individual firms. While most firms are required to pay UI tax for their employees, some types of employees are exempt from their states’ UI tax laws but are still within scope for the CES survey. Examples of the types of employees that may be exempt are: college students paid by their school as part of a work study program; interns of hospitals paid by the hospital for which they work; employees paid by state and local government and elected officials; independent or contract insurance agents; employees of nonprofits and religious organizations (the largest group of employees not covered); and railroad employees covered under a different system of UI administered by the RRB. This employment needs to be accounted for in order to set the benchmark level for CES employment.
State workforce agencies (SWAs) are responsible for providing monthly counts of noncovered employment to BLS as part of the annual benchmarking process. Laws on UI coverage vary from state to state, and SWAs review changes to these laws each year in order to identify industries where noncovered employment may be present. In several states, corporate officers are exempt from UI coverage, and, as a result, noncovered employment exists in most NAICS industries in those states. Noncovered values for corporate officers in Idaho, North Dakota, Oregon, and Washington, and other state-specific UI exemptions are used in benchmarking the CES national as well as state and area estimates.
No single source of noncovered data exists; therefore, SWAs use several sources to generate the employment counts, including County Business Patterns (CBP) and the Annual Survey of Public Employment and Payroll (ASPEP), both from the US Census Bureau; the RRB; state-conducted surveys, and other administrative data available to the state.
CES also develops national noncovered levels for March of the benchmark year, extrapolates these levels to each state (based on the state submitted values during the previous year), and provides the state-specific levels to the SWAs, as shown in equation 17.
![]()
where,
![]()
![]()
![]()
![]()
![]()
These values are used in benchmarking state and area employment when more accurate values are unavailable. For information on how the CES national noncovered values are derived, see calculation section of the CES-N Handbook of Methods.
The primary source used in constructing new CES-SA employment time series is the BLS longitudinal database (LDB), which consists of establishment-level microdata from the QCEW and represents all employment covered by the UI system. The LDB contains the state, county, township, ownership (private industry; or federal, state, or local government), and NAICS codes that were assigned to each establishment in a given quarter. The LDB connects businesses reporting to the UI system across time in two ways that aid in reconstructing employment time series. First, establishments that changed UI account numbers but represent the same business location are linked together with a common identifier (a unique “LDB number” for each establishment). Second, the LDB tracks more complicated predecessor–successor relationships where changes in reporting may be administrative rather than economic in nature. These kinds of relationships may exist when old and new UI reporting units share some physical assets but do not represent the exact same worksites. An example is a firm that changes from reporting all of its jobs in one report to reporting separately about individual worksites. The establishments newly reported on do not represent actual business births, so it would be reasonable to impute some of the predecessor’s employment data onto them prior to the date of the administrative change. For time-series construction, each establishment involved in a predecessor–successor transaction is given an adjustment value based on its most recent relationship. For example, if a worksite represented 10 percent of its firm’s employment when reporting was broken out in detail, then, prior to that point in time, 10 percent of its firm’s reported employment would have been imputed to that worksite.
Industry, area, and ownership code changes, which may be for either economic or noneconomic reasons, also occur in the LDB. Economic code changes represent a change in business activity that was denoted in the quarter it occurred. These changes are included in the time series. Unlike economic code changes, noneconomic code changes (NECCs) are administrative in nature and therefore are adjusted before their inclusion in a time series, in order to eliminate series breaks. With the aim of reducing the number of noneconomic breaks, the LDB is adjusted so that each establishment was given its final (i.e., most recently assigned) codes.
The sum of LDB employment—adjusted for predecessor–successor transactions—is then tallied for each industry, county, township, and ownership level. To these totals, employment data for LDB records with unclassified county or town codes is distributed on the basis of the proportion of employment in each county and town, for every NAICS and ownership code. Employment data associated with unassigned NAICS codes are distributed proportionally to other industries within a county or town. Records that lack NAICS and county or town codes are distributed to counties and towns on the basis of their proportion of total CES-assigned employment within the state and then distributed proportionally to all industries.
The CES program works with states each year to review UI laws and determine an appropriate noncovered employment (NCE) value for each industry and area, as described in the section on benchmarking. In developing new series constructions, NCE values are derived for the most recent year, and ratios of noncovered-to-covered employment are calculated and used to estimate historical NCE level.
Regular faculty members with contracts of at least 1 year at primary and secondary schools, colleges, and universities are counted as employed for the entire year in the CES survey, whether or not they receive pay year round. Many school faculty members do not get paid during summer breaks and are not counted under QCEW employment definitions, creating an additional difference in scope that requires adjustment.
Noncovered employment totals and summer faculty adjustments are added to the sum of LDB employment when new AE series are constructed.
When new series are added for non-AE data types, the available matched sample is used to construct histories. An initial sample average is calculated to provide a starting point for the series and then the sample data are processed through the robust weighted link and taper.
Time series published by CES-SA can exhibit regularly recurring seasonal movements. Seasonal adjustment eliminates the part of the series attributable to normal seasonal variation and makes it possible to observe the cyclical and other non-seasonal movements in CES-SA series. Seasonally adjusted series are published monthly for selected nonfarm payroll employment estimates.
CES-SA uses the X-13ARIMA-SEATS software, developed and maintained by the U.S. Census Bureau, to seasonally adjust CES-SA. Models are set annually, and seasonal adjustment is performed on a concurrent basis. The X-13ARIMA-SEATS software is available on the U.S. Census Bureau website at https://www.census.gov/data/software/x13as.html.
CES-SA defaults to using 10 years of data as an input to X-13ARIMA-SEATS. If a historical correction prior to the default ten years was made during the annual benchmarking process, the start year of the input universe time series will be the earliest corrected year. For newly published series, a minimum of 3 years of data is required before the series can be processed by X-13ARIMA-SEATS.
Because of the nature of the CES program, BLS controls for survey interval variations, sometimes referred to as the 4- versus 5-week effect, during seasonal adjustment. Although the CES survey is referenced to a consistent concept—the pay period including the 12th of each month—inconsistencies arise because there are sometimes 4 and sometimes 5 weeks between the weeks including the 12th in a given pair of months. In highly seasonal industries, these variations can be an important determinant of the magnitude of seasonal hires or layoffs that have occurred at the time the survey is taken, thereby complicating seasonal adjustment.
Standard seasonal adjustment methodology relies heavily on the experience of the most recent three years to determine the expected seasonal change in employment for each month of the current year. Prior to the implementation of the adjustment, the procedure did not distinguish between 4- and 5-week survey intervals, and the accuracy of the seasonal expectation depended in large measure on how well the current year's survey interval corresponded with those of the previous 3 years. All else equal, the greatest potential for distortion occurred when the current month being estimated had a 5-week interval but the 3 years preceding it were all 4-week intervals; or, conversely, when the current month had a 4-week interval but the three years preceding it were all 5-week intervals.
BLS uses REGARIMA (regression with autocorrelated errors) modeling to identify the estimated size and significance of the calendar effect for each published series. REGARIMA combines standard regression analysis, which measures the numerical relationship among two or more variables, with ARIMA modeling, which describes and predicts the behavior of data series based on its own history. For many economic time series, including nonfarm payroll employment, observations are auto-correlated over time; each month's value is significantly dependent on the observations that precede it. These series, therefore, usually can be successfully fit using ARIMA models. If autocorrelated time series are modeled through regression analysis alone, the measured relationships among other variables of interest may be distorted because of the influence of the autocorrelation. Thus, the REGARIMA technique is appropriate for measuring relationships among variables of interest in series that exhibit autocorrelation, such as nonfarm payroll employment.
In this application, the relationships of interest are those between employment levels in individual calendar months and the lengths of the survey intervals for those months. The REGARIMA models evaluate the variation in employment levels attributable to eleven separate survey interval variables, one specified for each month, except March. March is excluded because there are almost always 4 weeks between the February and March surveys. Models for individual basic series are fit with the most recent ten years of data available, the standard time span used for CES seasonal adjustment.
The REGARIMA procedure yields regression coefficients for each of the 11 months specified in the model. These coefficients provide estimates of the strength of the relationship between employment levels and the number of weeks between surveys for the 11 modeled months. The X-13ARIMA-SEATS software also produces diagnostic statistics that permit the assessment of the statistical significance of the regression coefficients, and all series are reviewed for model adequacy.
Because the 11 coefficients derived from the REGARIMA models provide an estimate of the magnitude of variation in employment levels associated with the length of the survey interval, these coefficients are used to adjust the CES data to remove the calendar effect.
CES-SA uses a two-step seasonal adjustment method to address the hybrid nature of the time series, which consist of universe data through the latest benchmark month followed by sample data up to the current month. The seasonal variations of these two data sources can differ and cause distortions in the seasonally adjusted data unless adjusted separately.
Beginning with January 1994 data, BLS implemented an alternative method that separately adjusts each part of the time series, an approach first carried out by Berger and Phillips.5 This method uses the seasonal trends found in universe-derived employment counts to adjust historical benchmark employment data while also incorporating sample-based seasonal trends to adjust sample-based employment estimates. These two series are independently adjusted then spliced together at the October re-estimate point. By accounting for the differing seasonal patterns found in historical benchmark employment data and the sample-based employment estimates, this technique yields improved seasonally adjusted series with respect to analysis of month-to-month employment change.
With the release of January 2018 data, CES-SA converted to concurrent seasonal adjustment, which uses all available estimates, including those for the current month, in developing sample-based seasonal factors. Previously, CES-SA projected sample-based seasonal factors once a year during the annual benchmark process and applied those projected seasonal factors to the not seasonally adjusted monthly estimates over the following year. More information on CES-SA’s use of concurrent seasonal adjustment is available at https://www.bls.gov/sae/seasonal-adjustment/implementation-of-concurrent-seasonal-adjustment-for-ces-state-and-area-estimates.htm.
CES-SA publishes seasonally adjusted data for nonfarm payroll employment series at the supersector and sector levels, as well as total nonfarm (TNF) for published metropolitan areas that have sufficient sample history and satisfy criteria for seasonal adjustment. Revisions of historical data for the most recent 5 years, where available, are made once a year, coincident with annual benchmark adjustments. If a historical correction is issued to the unadjusted supersector or sector series prior to the standard 5-year replacement period, seasonally adjusted data will be revised back to the earliest historically corrected year.
The aggregation method of seasonally adjusted data is based upon the availability of underlying industry data. For all 50 states, the District of Columbia, and Puerto Rico, the following series are sums of underlying industry data: total private, goods-producing, service-providing, and private service-providing. The same method is applied for the U.S. Virgin Islands with the exception of goods-producing, which is independently seasonally adjusted because of data limitations. For all 50 states, the District of Columbia, Puerto Rico, and the U.S. Virgin Islands, seasonally adjusted data for manufacturing, trade, transportation, and utilities, financial activities, education and health services, leisure and hospitality, and government are aggregates wherever exhaustive industry components are available seasonally adjusted; otherwise, these industries’ employment data are directly seasonally adjusted. In a very limited number of cases, the not seasonally adjusted data for mining; construction; manufacturing; trade, transportation, and utilities; financial activities; education and health services; leisure and hospitality; and government do not exhibit enough seasonality to be adjusted; in those cases, the not seasonally adjusted data are used to sum to higher level industries. The seasonally adjusted total nonfarm data for all MSAs and metropolitan divisions are not an aggregation but are derived directly by applying the seasonal adjustment procedure to the not seasonally adjusted total nonfarm level.
Derivative series, plus annual and quarterly averages, are data derived from sample-based estimates. All hours and earnings derivative data are calculated for both AE and PE using their respective sample-based employment, hours, and earnings estimates. The following equations describe how these data are calculated.
![]()
![]()
![]()
![]()
where,
13 = annual average. (Note: When accessing these data via the public access tool then annual averages are shown as M13.)
![]()
where,
![]()
![]()
where,
![]()
Diffusion indexes are produced at the total nonfarm level as an aggregate of the 50 states and the District of Columbia, as well as an aggregate of 389 Metropolitan Statistical Areas (MSAs), over 1-, 3-, 6-, and 12-month time spans, and are used to measure the breadth of employment growth or decline. Seasonally adjusted data are used for all CES-SA diffusion indexes.6
To derive the indexes, calculate the employment change for the 1-, 3-, 6-, or 12-month span for each component state and MSA. They are assigned a value of 0 to each employment decrease, 50 to each unchanged observation, and 100 to each employment increase over the selected time span. The diffusion index is the average (mean) of the assigned values. Diffusion indexes above 50 indicate that employment in most states and areas increased over a given timespan, while values under 50 indicate that employment declined.
The CES survey, like other sample surveys, is subject to two types of error, sampling and nonsampling error. The magnitude of sampling error, or variance, is directly related to the size of the sample and the percentage of universe coverage achieved by the sample. The CES sample of about 131,000 businesses and government agencies covers over one-third of total universe employment on average, typically yielding a small variance for the statewide total nonfarm estimates.
The sum of sampling and nonsampling error represents total survey error. Unlike most sample surveys that publish sampling error as their only measure of error, the CES derives an annual approximation of total error using lagged and independently derived universe data. While the benchmark revision is often used as a proxy measure of total error for the CES survey estimate, the QCEW is also subject to some forms of measurement error (though not sampling error), and therefore the revision reflects the net of the errors present in each program.7 Benchmark revisions are published in the annual benchmark article for each state at the total nonfarm level, and summary statistics on the distribution of revisions are published for statewide supersectors and MSAs.
The CES-SA program publishes first preliminary estimates of employment, hours, and earnings based on less than the total sample—typically on the third Friday immediately following the reference month. Revised sample-based estimates are published during with the subsequent month’s preliminary estimates to allow for receipt of additional sample. Revisions are published on the BLS website each month.
The estimation of sample variance for AE, available on the BLS website, is accomplished through use of generalized variance functions (GVFs). The generalized variance function connects the variance of an estimator to a set of variables the variance depends on, such as the size of employment, the number of respondents, and the fraction of the population represented by the sample. Variances estimated directly from the sample may be unstable—especially in smaller domains. A model-based GVF is a way to stabilize direct estimates of variances.
The parameters of the model used for GVF are estimated by fitting the model to a set of direct replication-based variances obtained from the repeatedly grouped balanced half-samples (RGBHS) procedure. RGBHS is a modification of the balanced half-samples (BHS) technique used by the CES-N program.
The estimation of sample variance for CES-N estimates is accomplished through the Fay’s method of BHS. In the Fay’s BHS method, the sample is repeatedly divided into halves using a systematic technic. For each replicate division, the original sample weights are adjusted in both halves of the sample: weights for units that belong to one half of the sample are multiplied by a factor of ![]() , whereas weights for units in the other half of the sample are multiplied by a factor of
, whereas weights for units in the other half of the sample are multiplied by a factor of ![]() . Replicate estimates based on these adjusted weights are calculated using the same estimation formula as used for the full-sample estimate. The procedure is repeated k times. The BHS variance is calculated by measuring the variability of the replicate estimates as described in equation 21.
. Replicate estimates based on these adjusted weights are calculated using the same estimation formula as used for the full-sample estimate. The procedure is repeated k times. The BHS variance is calculated by measuring the variability of the replicate estimates as described in equation 21.
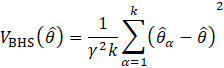
where,
![]()
![]()
![]()
![]()
RGBHS is a modification of BHS which involves the repeated calculation of BHS estimates R times. After each calculation, the sample units are randomly re-assigned to two groups in order to produce new BHS estimates. Finally, the RGBHS variance estimate is obtained by averaging the BHS variance estimates as
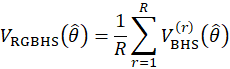
where,
R stands for rth reassignment of the random groups.
The GVF regressions is then used to smooth the RGBHS, as shown in equation 22.
![]()
where,
![]()
![]()
![]()
![]()
![]()
The GVF modeled variance estimates are then used for publication. More information on the generalized variance function can be found at https://www.bls.gov/osmr/research-papers/2013/pdf/st130050.pdf.
Variance statistics are useful for comparison purposes, but they do have some limitations. Variances reflect the error components of estimates that are due to surveying only a subset of the population, rather than conducting a complete count of the entire population; however, they do not reflect nonsampling error, such as response errors, bias due to nonresponse, and model error for modeled estimates. The variances of the over-the-month change estimates are very useful in determining when changes are significant at some level of confidence.
1 P.N. Kokic and P.A. Bell, “Optimal winsorizing cutoffs for a stratified finite population estimator,” Journal of Official Statistics, no. 10, (1994), pp. 419–35.
2 Fay, R. E., and Herriot, R. A. (1979), “Estimates of Income for Small Places: An Application of James - Stein Procedures to Census Data,” Journal of the American Statistical Association, no. 74, 269–77.
3 Julie Gershunskaya and Terrance D. Savitsky, “Bayesian nonparametric joint model for point estimates and variances,” in Office of Survey Methods Research, 2019 (U.S. Bureau of Labor Statistics, November 2019), https://www.bls.gov/osmr/research-papers/2019/st190020.htm.
4 Paige Schroeder, “How to catch an outlier: A robust method for hours and earnings estimation in the Current Employment Statistics Survey,”. in Office of Survey Methods Research, 2019 (U.S. Bureau of Labor Statistics, September 2019), https://www.bls.gov/osmr/research-papers/2019/st190070.htm.
5 Franklin D. Berger and Keith R. Phillips, “Solving the mystery of the disappearing January blip in state employment data,” Federal Reserve Bank of Dallas, 1994,https://www.dallasfed.org/~/media/documents/research/er/1994/er9402d.pdf..
6 TJ Lepoutre, “Diffusion indexes of state and metropolitan area employment changes,” Monthly Labor Review (March 2022), https://www.bls.gov/opub/mlr/2022/article/diffusion-indexes-of-state-and-metropolitan-area-employment-changes.htm.
7 Jeffrey Groen, “Sources of error in survey and administrative data: the importance of reporting procedures,” Journal of Official Statistics, no. 28, (2012), pp. 173–98.