An official website of the United States government
 United States Department of Labor
United States Department of Labor
U.S. Import and Export Price Indexes are currently calculated with a modified Laspeyres formula at each level of aggregation. However, the geometric Young formula might be more appropriate for the first two levels of aggregation, which are the weight group and the classification group. If the geometric Young formula was used to calculate inflation from 2012 to 2022, then cumulative headline inflation would have decreased from 10.0 to 5.8 percent for imports and from 14.7 to 9.5 percent for exports. Half of this change comes from using the geometric Young formula at the weight-group level, and the other half comes from the classification-group level.
The U.S. Import and Export Price Indexes (MXPIs), calculated by the U.S. Bureau of Labor Statistics (BLS), have many uses, including deflating trade values for gross domestic product estimates and assessing terms of trade. The formula used to calculate these indexes affects our understanding of the U.S. trade deficit and the estimates of other economic indicators.
In this article, we examine historical MXPIs by using the geometric Young formula at the two lowest index levels, which are the weight-group level and the classification-group level. MXPIs are currently calculated with a modified Laspeyres (Lowe) formula through multiple levels of aggregation between input prices and an output headline index.1 In the current calculation process, prices collected for a given company in a given product area are first aggregated to the weight group, which consists of combining prices in the product area within a company. Second, weight groups are aggregated to the classification group. Third, classification-group indexes are aggregated by using three different trees based on various classification systems, and each tree group’s products are put into broader product categories. This article studies modifications to the first two levels of aggregation and their affect on the Harmonized System (HS) tree, which is the classification system for tariffs that aggregates 10-digit HS codes (or classification groups) into two- and four-digit HS codes.2
BLS uses the geometric Young formula at the elementary level for the U.S. Consumer Price Index (CPI) and for a research-level Producer Price Index (PPI). Since 1999, BLS has applied the geometric Young formula in many CPI product areas to average item prices because that formula better approximates a cost-of-living index.3 In 2024, BLS began to publish research PPIs by using the geometric Young formula after extensive research into the formula’s impact.4 BLS undertook this research because the geometric Young formula has some advantages from both an economic and statistical approach to index theory. From an economic approach, the geometric Young formula can better approximate a fixed input–output price index. From a statistical approach, an appropriately weighted geometric Young formula satisfies the time reversal test.5
The target index concept for the MXPIs should be some combination of the target for the CPI and PPI because the MXPIs mixes final and intermediate goods. Therefore, it makes sense to study the geometric Young formula in the context of the MXPIs. Additionally, using the geometric Young formula in all three price programs at the lowest level would add consistency in the indexes, and the indexes would be more comparable. The CPI and PPI programs use the geometric Young formula at the elementary aggregate index level, which is comparable to the classification-group level in the MXPIs. Thus, we consider the impact of the geometric Young formula at that level in this article.6
The geometric Young index is always lower than a modified Laspeyres index with identical weights. However, the magnitude of replacing a Laspeyres index with a geometric Young index is unclear. Almost 50 percent of weight groups have only one item. In those cases, formula choice has no impact. On the other hand, about 20 percent of weight groups contain at least four items. In those cases, formula choice can have a substantial impact.
In comparing the results using the HS tree, we find that, between 2012 and 2022, cumulative headline inflation would have decreased from 10.0 percent to 5.8 percent for imports and from 14.7 percent to 9.5 percent for exports. Half of this change comes from using the geometric Young formula at the weight-group level, and the other half of this change comes at the classification-group level.
There is variation in the formula's impact on four-digit HS indexes. For example, 30.4 percent of indexes have changes between 0.0 and 0.1 percentage point per year. However, some indexes experience large changes; 22.4 percent of indexes have changes that exceed 0.5 percentage point per year.
Finally, we perform a back-of-the-envelope calculation of the real trade deficit over time when MXPIs are calculated by using the geometric Young formula. Although the price indexes for imports and exports decline by similar amounts, the impact on the dollar value of imports is larger. When the current real trade deficit is calculated with a geometric Young formula instead of a Laspeyres formula, it is about 2 percentage points greater in 2012 U.S. dollars.
In the remainder of this article, we first provide an overview of the current MXPIs methodology and the changes that we are studying. Next, we estimate the impact of switching to the geometric Young formula at the first two levels of aggregation. Finally, we provide more details about the underlying sources of the differences between the geometric Young and Laspeyres formulas.
In this section, we describe the data used for our analysis. Also, we describe the current methodology used to calculate the MXPIs and how well we can replicate the published MXPIs with our data.
To examine the practical use of the geometric Young formula for index calculation, we use price data from the MXPIs research database from 2012 through 2022. This research database provides snapshots of the MXPIs production database for use by non-BLS researchers working within a restricted-access environment.7 We use these data to replicate MXPIs with the current methodology and also to calculate indexes with alternative formulas. Throughout, we aggregate by using the U.S. harmonized tariff schedule for imports and schedule B statistical classification for exports (hereafter referred to as Harmonized System code or HS code).8 We use the HS classification tree because it is the basis for imputing missing values in the two other trees, which are the North American Industrial Classification System and the end-use classification system developed by the U.S. Bureau of Economic Analysis.
BLS calculates MXPIs by aggregating item prices into broader groups, such as weight groups, classification groups, and stratum groups that follow the HS schedule. Each of these aggregation steps uses a modified Laspeyres, which is calculated by using the current price, the previous price, and the weight of an item within its next group. The weights are derived by dollar value and probability of selection into the sample. In the sections below, we describe how we calculate indexes by following the methods in the MXPIs chapter of the BLS Handbook of Methods, with the exception that we do not preimpute for new items.9
The basic unit of observation for MXPIs is the price for an item i in a month t, which is written as pi,t. Each of these prices has an associated weight that is either a sample weight or trade-dollar weight in some base period b.10 The weight association with pi,t in a period is qi,b, in which b is the base period. The first step is to aggregate prices to the weight-group level. Let Iw be the set of items in weight-group w, then the monthly change in an index or a short-term relative (STR) is
After this step, we calculate an index for each weight group as follows:
with lw,b = 100![]() We do not consider this the elementary index because about 50 percent of weight groups have only one item; if this is the case, then the index calculated in this step simply reflects a normalized price.
We do not consider this the elementary index because about 50 percent of weight groups have only one item; if this is the case, then the index calculated in this step simply reflects a normalized price.
In the next step, the weight-group indexes are aggregated to classification-group indexes. If we let Wc be the set of weight groups in classification-group c, we calculate the classification-group STR as follows:
The result of equation (3) is converted to an index level by starting the index at 100 in January 2012 and advancing it by using pc,t. Therefore, the index level for a product category in a month is lc,t = lc,t–1 pc,t, with lc,b = 100.
Because we focus on aggregating indexes through the HS tree, we calculate them at the two- and four-digit HS levels. In each case, the classification-group indexes are aggregated by using trade weights from the base period and the index calculated in equation (3).
The official headline MXPIs are based on the U.S. Bureau of Economic Analysis end-use tree. However, our focus is on replicating the HS tree because we can replicate the official MXPIs methodology best in that tree. Thus, we calculate our own version of the headline MXPIs based on the HS tree for top-level comparisons. We do this both for the modified Laspeyres indexes and the geometric Young indexes.
Using the formulas described above, we compare our calculated results for the official MXPIs numbers with two- and four-digit HS indexes.11 We split indexes into three categories based on the following three statistics: a correlation coefficient, a mean absolute error, and a root-mean-square error of the month-to-month changes of the indexes. The correlation coefficient captures whether our index moves in the same direction as the official index. The other two statistics measure the average difference between the changes in the indexes, with the root-mean-square error penalizing outliers more.
We classify indexes into three different groups depending on the value of the aforementioned three statistics. When comparing the month-to-month changes of the calculated index with the official index, we define an extremely well replicated index as one that satisfies all three of the following criteria: a correlation coefficient above 0.85, a root-mean-square error less than 2.0, and a mean absolute error less than 1.0. Indexes that meet these criteria are visually almost identical to the official index. A well-replicated index is one that satisfies all three criteria at a lower standard: a correlation coefficient above 0.2, a root-mean-square error below 5.0, and a mean absolute error less than 2.0. An index is considered not well replicated if it does not meet these statistical criteria. The purpose of these cutoffs is to eliminate any indexes that cannot be replicated because the MXPIs research data differs from the MXPIs production data or because an index is affected by parts of the MXPIs methodology that we did not replicate, such as preimputing. Typically, when an index is not well replicated, the version we calculate has large changes that are not present in the official index. It would not be appropriate to investigate the impact of geometric Young formula on these indexes because we would mechanically find a large impact since the geometric Young formula will suppress large increases. Thus, our results on the impact of switching to the geometric Young formula would be biased toward finding a large impact.
Fortunately, we were able to replicate almost all indexes well. At the two- and four-digit levels, we find 84 indexes that were replicated extremely well and 251 indexes that were replicated well. These indexes accounted for over 96 percent of the value of imports and over 90 percent of the value of exports in 2022. We were unable to replicate only 26 indexes well. We exclude these indexes from our calculation of headline indexes. Examples of the replication are shown in charts 1 and 2.
| Month | Calculated index | Official index |
|---|---|---|
| January 2012 | 100.00 | 100.00 |
| February 2012 | 99.61 | 99.60 |
| March 2012 | 102.17 | 102.18 |
| April 2012 | 102.43 | 102.41 |
| May 2012 | 101.74 | 102.18 |
| June 2012 | 92.50 | 92.92 |
| July 2012 | 111.42 | 111.47 |
| August 2012 | 123.43 | 123.48 |
| September 2012 | 120.35 | 120.40 |
| October 2012 | 116.84 | 116.87 |
| November 2012 | 115.77 | 115.74 |
| December 2012 | 117.96 | 117.89 |
| January 2013 | 107.81 | 107.87 |
| February 2013 | 113.62 | 113.62 |
| March 2013 | 111.65 | 111.67 |
| April 2013 | 102.20 | 102.28 |
| May 2013 | 104.85 | 104.83 |
| June 2013 | 107.47 | 107.28 |
| July 2013 | 103.76 | 103.57 |
| August 2013 | 88.28 | 88.19 |
| September 2013 | 85.44 | 85.35 |
| October 2013 | 74.15 | 74.07 |
| November 2013 | 72.91 | 72.85 |
| December 2013 | 73.52 | 73.48 |
| January 2014 | 72.74 | 72.65 |
| February 2014 | 75.36 | 75.26 |
| March 2014 | 80.97 | 80.85 |
| April 2014 | 82.87 | 82.64 |
| May 2014 | 82.50 | 82.18 |
| June 2014 | 75.72 | 75.36 |
| July 2014 | 69.97 | 69.68 |
| August 2014 | 65.44 | 65.18 |
| September 2014 | 62.72 | 62.57 |
| October 2014 | 58.79 | 58.66 |
| November 2014 | 64.87 | 64.68 |
| December 2014 | 64.75 | 64.58 |
| January 2015 | 65.53 | 65.28 |
| February 2015 | 63.42 | 63.16 |
| March 2015 | 64.15 | 63.89 |
| April 2015 | 63.52 | 63.26 |
| May 2015 | 61.44 | 61.24 |
| June 2015 | 60.06 | 59.89 |
| July 2015 | 68.04 | 67.82 |
| August 2015 | 60.40 | 60.12 |
| September 2015 | 59.12 | 58.83 |
| October 2015 | 62.63 | 62.80 |
| November 2015 | 62.01 | 62.20 |
| December 2015 | 59.44 | 59.59 |
| January 2016 | 57.74 | 57.47 |
| February 2016 | 60.56 | 60.32 |
| March 2016 | 57.38 | 57.18 |
| April 2016 | 57.35 | 57.31 |
| May 2016 | 61.49 | 61.47 |
| June 2016 | 65.28 | 65.18 |
| July 2016 | 59.51 | 59.06 |
| August 2016 | 57.25 | 57.04 |
| September 2016 | 54.74 | 54.56 |
| October 2016 | 56.04 | 56.02 |
| November 2016 | 56.91 | 56.85 |
| December 2016 | 55.50 | 55.49 |
| January 2017 | 57.92 | 57.94 |
| February 2017 | 59.39 | 59.39 |
| March 2017 | 60.85 | 60.88 |
| April 2017 | 57.79 | 57.57 |
| May 2017 | 57.94 | 57.71 |
| June 2017 | 58.30 | 58.07 |
| July 2017 | 58.73 | 58.50 |
| August 2017 | 55.57 | 55.36 |
| September 2017 | 53.29 | 53.11 |
| October 2017 | 54.09 | 54.33 |
| November 2017 | 54.62 | 54.89 |
| December 2017 | 54.98 | 55.19 |
| January 2018 | 55.89 | 56.32 |
| February 2018 | 60.19 | 60.65 |
| March 2018 | 62.28 | 62.73 |
| April 2018 | 62.39 | 62.83 |
| May 2018 | 65.21 | 65.67 |
| June 2018 | 63.03 | 63.49 |
| July 2018 | 57.27 | 57.67 |
| August 2018 | 59.14 | 59.66 |
| September 2018 | 57.88 | 58.40 |
| October 2018 | 57.45 | 57.90 |
| November 2018 | 58.65 | 59.13 |
| December 2018 | 59.80 | 60.28 |
| January 2019 | 59.35 | 1 |
| February 2019 | 61.56 | 61.54 |
| March 2019 | 61.28 | 61.14 |
| April 2019 | 59.59 | 59.46 |
| May 2019 | 59.08 | 58.96 |
| June 2019 | 67.79 | 67.69 |
| July 2019 | 68.53 | 68.42 |
| August 2019 | 63.87 | 63.79 |
| September 2019 | 56.45 | 56.35 |
| October 2019 | 60.94 | 60.85 |
| November 2019 | 62.07 | 61.97 |
| December 2019 | 61.57 | 61.47 |
| January 2020 | 62.88 | 62.80 |
| February 2020 | 62.77 | 62.67 |
| March 2020 | 62.31 | 62.30 |
| April 2020 | 55.57 | 55.52 |
| May 2020 | 51.99 | 52.08 |
| June 2020 | 54.32 | 54.33 |
| July 2020 | 57.25 | 57.28 |
| August 2020 | 52.95 | 52.94 |
| September 2020 | 58.99 | 58.99 |
| October 2020 | 63.68 | 63.69 |
| November 2020 | 68.59 | 68.62 |
| December 2020 | 69.87 | 69.91 |
| January 2021 | 80.54 | 80.59 |
| February 2021 | 88.42 | 88.49 |
| March 2021 | 88.30 | 87.47 |
| April 2021 | 89.68 | 88.82 |
| May 2021 | 116.23 | 115.15 |
| June 2021 | 109.09 | 107.80 |
| July 2021 | 106.95 | 106.02 |
| August 2021 | 100.61 | 99.74 |
| September 2021 | 88.12 | 87.47 |
| October 2021 | 89.43 | 88.72 |
| November 2021 | 92.00 | 91.27 |
| December 2021 | 93.86 | 92.63 |
| January 2022 | 98.53 | 97.16 |
| February 2022 | 102.90 | 101.32 |
| March 2022 | 117.69 | 115.31 |
| April 2022 | 122.53 | 119.68 |
| May 2022 | 128.24 | 125.30 |
| June 2022 | 119.02 | 117.63 |
| July 2022 | 117.95 | 116.47 |
| August 2022 | 111.35 | 110.25 |
| September 2022 | 111.51 | 110.42 |
| October 2022 | 113.22 | 112.14 |
| November 2022 | 120.48 | 119.28 |
| December 2022 | 107.97 | 106.75 |
| 1 This index was not published in January 2019 because the data source was not available due to the government shutdown. Note: An extremely well replicated index is one that has a correlation coefficient above 0.85, a root-mean-square error less than 2.0, and a mean absolute error less than 1.0 when comparing the short-term relatives of the calculated to the official index. A well-replicated index is one that has a correlation coefficient above 0.2, a root-mean-square error below 5.0, and a mean absolute error less than 2.0. All other indexes are considered not well replicated. Source: U.S. Bureau of Labor Statistics. | ||
| Month | Calculated index | Official index |
|---|---|---|
| January 2012 | 100.00 | 100.00 |
| February 2012 | 104.68 | 102.47 |
| March 2012 | 103.84 | 107.30 |
| April 2012 | 104.56 | 110.66 |
| May 2012 | 100.34 | 104.12 |
| June 2012 | 100.80 | 93.58 |
| July 2012 | 101.52 | 94.76 |
| August 2012 | 105.59 | 100.41 |
| September 2012 | 99.59 | 106.45 |
| October 2012 | 98.18 | 106.69 |
| November 2012 | 109.43 | 98.11 |
| December 2012 | 110.71 | 97.64 |
| January 2013 | 108.99 | 98.88 |
| February 2013 | 104.81 | 103.92 |
| March 2013 | 104.63 | 103.53 |
| April 2013 | 111.68 | 98.97 |
| May 2013 | 115.92 | 95.82 |
| June 2013 | 121.44 | 96.20 |
| July 2013 | 120.44 | 98.97 |
| August 2013 | 114.20 | 102.06 |
| September 2013 | 112.96 | 103.65 |
| October 2013 | 112.43 | 97.73 |
| November 2013 | 105.16 | 99.62 |
| December 2013 | 107.33 | 105.18 |
| January 2014 | 107.55 | 104.57 |
| February 2014 | 109.53 | 106.42 |
| March 2014 | 112.07 | 108.78 |
| April 2014 | 108.11 | 99.88 |
| May 2014 | 108.69 | 100.41 |
| June 2014 | 106.51 | 98.26 |
| July 2014 | 107.88 | 99.47 |
| August 2014 | 104.89 | 96.85 |
| September 2014 | 104.20 | 96.52 |
| October 2014 | 97.40 | 90.66 |
| November 2014 | 88.96 | 83.06 |
| December 2014 | 76.46 | 72.78 |
| January 2015 | 61.22 | 58.32 |
| February 2015 | 64.57 | 62.44 |
| March 2015 | 67.46 | 65.51 |
| April 2015 | 63.22 | 61.03 |
| May 2015 | 69.58 | 67.51 |
| June 2015 | 67.30 | 67.39 |
| July 2015 | 64.75 | 65.13 |
| August 2015 | 57.09 | 58.03 |
| September 2015 | 53.98 | 54.70 |
| October 2015 | 53.39 | 54.23 |
| November 2015 | 51.73 | 52.40 |
| December 2015 | 45.66 | 46.36 |
| January 2016 | 41.15 | 41.27 |
| February 2016 | 38.72 | 38.32 |
| March 2016 | 40.42 | 39.35 |
| April 2016 | 41.40 | 41.27 |
| May 2016 | 46.97 | 46.95 |
| June 2016 | 51.26 | 52.81 |
| July 2016 | 48.93 | 50.99 |
| August 2016 | 45.55 | 47.86 |
| September 2016 | 48.74 | 51.55 |
| October 2016 | 53.00 | 55.38 |
| November 2016 | 50.74 | 53.64 |
| December 2016 | 52.93 | 55.99 |
| January 2017 | 54.35 | 57.11 |
| February 2017 | 53.80 | 55.73 |
| March 2017 | 52.54 | 54.82 |
| April 2017 | 54.09 | 56.94 |
| May 2017 | 50.54 | 52.84 |
| June 2017 | 51.13 | 53.37 |
| July 2017 | 50.49 | 52.99 |
| August 2017 | 55.31 | 58.35 |
| September 2017 | 60.58 | 63.30 |
| October 2017 | 57.66 | 59.88 |
| November 2017 | 61.67 | 63.71 |
| December 2017 | 60.81 | 62.44 |
| January 2018 | 64.28 | 66.39 |
| February 2018 | 64.46 | 66.69 |
| March 2018 | 63.04 | 64.62 |
| April 2018 | 65.80 | 67.54 |
| May 2018 | 70.24 | 71.84 |
| June 2018 | 69.42 | 71.99 |
| July 2018 | 70.49 | 73.05 |
| August 2018 | 69.92 | 72.64 |
| September 2018 | 71.14 | 73.37 |
| October 2018 | 76.28 | 78.17 |
| November 2018 | 66.60 | 70.04 |
| December 2018 | 57.51 | 60.62 |
| January 2019 | 55.39 | 58.94 |
| February 2019 | 60.29 | 62.33 |
| March 2019 | 64.59 | 66.92 |
| April 2019 | 66.79 | 69.31 |
| May 2019 | 67.13 | 69.69 |
| June 2019 | 60.64 | 63.98 |
| July 2019 | 63.32 | 66.51 |
| August 2019 | 60.49 | 64.18 |
| September 2019 | 59.96 | 63.56 |
| October 2019 | 60.71 | 64.30 |
| November 2019 | 62.57 | 64.62 |
| December 2019 | 60.09 | 63.48 |
| January 2020 | 63.29 | 66.42 |
| February 2020 | 53.47 | 58.47 |
| March 2020 | 51.75 | 55.79 |
| April 2020 | 33.54 | 35.91 |
| May 2020 | 30.06 | 34.64 |
| June 2020 | 39.23 | 42.03 |
| July 2020 | 41.28 | 44.59 |
| August 2020 | 41.39 | 44.39 |
| September 2020 | 40.97 | 44.89 |
| October 2020 | 40.25 | 43.95 |
| November 2020 | 40.43 | 43.21 |
| December 2020 | 45.67 | 48.57 |
| January 2021 | 50.74 | 53.49 |
| February 2021 | 55.20 | 58.56 |
| March 2021 | 61.36 | 65.95 |
| April 2021 | 60.12 | 65.13 |
| May 2021 | 65.11 | 69.96 |
| June 2021 | 68.16 | 72.28 |
| July 2021 | 69.52 | 73.78 |
| August 2021 | 67.46 | 73.02 |
| September 2021 | 69.13 | 74.17 |
| October 2021 | 76.56 | 81.27 |
| November 2021 | 75.48 | 82.03 |
| December 2021 | 67.61 | 73.08 |
| January 2022 | 75.76 | 82.30 |
| February 2022 | 87.60 | 94.99 |
| March 2022 | 111.24 | 117.03 |
| April 2022 | 108.98 | 114.70 |
| May 2022 | 134.86 | 134.43 |
| June 2022 | 131.89 | 140.35 |
| July 2022 | 112.38 | 122.06 |
| August 2022 | 101.20 | 105.98 |
| September 2022 | 107.79 | 105.21 |
| October 2022 | 115.86 | 116.14 |
| November 2022 | 116.26 | 113.61 |
| December 2022 | 86.04 | 89.69 |
| Note: An extremely well replicated index is one that has a correlation coefficient above 0.85, a root-mean-square error less than 2.0, and a mean absolute error less than 1.0 when comparing the short-term relatives of the calculated to the official index. A well-replicated index is one that has a correlation coefficient above 0.2, a root-mean-square error below 5.0, and a mean absolute error less than 2.0. All other indexes are considered not well replicated. Source: U.S. Bureau of Labor Statistics. | ||
In this section, we evaluate the impact of using the geometric Young formula at both the classification-group level and the weight-group level. All other aggregations are based on the modified Laspeyres method currently in use. We perform this comparison by using only the indexes that we were able to replicate well with the MXPIs research database. Replication of the original modified Laspeyres method is necessary for comparison because it avoids errors that may arise with imperfect replication of the true MXPIs series. Thus, we modify the Laspeyres method at the classification-group level and the weight-group level using equations (4) and (6) instead of equations (1) and (3). The geometric Young formula for the weight group is
Some equation manipulation is required in order to keep the weights consistent between the geometric Young calculation and the Laspeyres calculation. If we rewrite the modified Laspeyres equation as
then it is exactly equivalent to equation (1). If we express the equation
![]()
as the exponent in equation (4), then equation (4) allows for a direct comparison between the Laspeyres calculation and the geometric Young calculation using consistent weighting. This result implies that the geometric index is always less than the Laspeyres. The geometric Young calculation at the classification-group level would be based on the following equation:
where
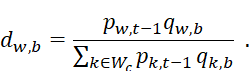
In this section, we compare indexes calculated with a modified Laspeyres method with indexes calculated with the geometric Young method. This comparison is conducted at either the classification-group and weight-group levels or only the weight-group level. We compare indexes that replicated well or extremely well.
We compare the series by studying index levels and by using the average difference between 12-month inflation rates, which is the same metric that the PPI program has used in evaluating the impact of the geometric Young formula.12 The geometric index is always less than the Laspeyres index with identical weights.13
In charts 3 and 4, we compare a Laspeyres calculation, a geometric Young calculation at just the weight-group level, and a geometric Young calculation at the weight- and classification-group levels. If the geometric Young calculation had been used, then the estimates for headline import and export inflation would have been, respectively, 4.2 and 5.2 percentage points lower between 2012 and 2022. Our estimate of headline inflation for imports was 10.0 percent and for exports was 14.7 percent over the entire study, which implies that the geometric Young formula lowers estimates of inflation by about one-fifth. On average, the 12-month inflation rates are 0.37 percentage point lower for imports and 0.46 percentage point lower for exports.
| Month | Laspeyres index | Geometric index at the weight-group level | Geometric index at the weight-group and classification-group levels |
|---|---|---|---|
| January 2012 | 100.00 | 100.00 | 100.00 |
| February 2012 | 99.96 | 99.93 | 99.88 |
| March 2012 | 100.39 | 100.35 | 100.27 |
| April 2012 | 100.47 | 100.41 | 100.30 |
| May 2012 | 100.30 | 100.23 | 100.10 |
| June 2012 | 99.93 | 99.86 | 99.71 |
| July 2012 | 99.77 | 99.67 | 99.51 |
| August 2012 | 99.52 | 99.42 | 99.24 |
| September 2012 | 99.61 | 99.49 | 99.30 |
| October 2012 | 99.99 | 99.86 | 99.65 |
| November 2012 | 99.89 | 99.74 | 99.52 |
| December 2012 | 99.79 | 99.64 | 99.40 |
| January 2013 | 99.57 | 99.38 | 99.10 |
| February 2013 | 99.63 | 99.43 | 99.13 |
| March 2013 | 99.61 | 99.39 | 99.06 |
| April 2013 | 99.52 | 99.26 | 98.90 |
| May 2013 | 98.95 | 98.67 | 98.28 |
| June 2013 | 98.57 | 98.28 | 97.88 |
| July 2013 | 98.13 | 97.83 | 97.42 |
| August 2013 | 98.09 | 97.77 | 97.35 |
| September 2013 | 98.25 | 97.92 | 97.48 |
| October 2013 | 98.41 | 98.06 | 97.61 |
| November 2013 | 98.51 | 98.16 | 97.69 |
| December 2013 | 98.29 | 97.93 | 97.46 |
| January 2014 | 98.51 | 98.11 | 97.62 |
| February 2014 | 98.45 | 98.05 | 97.54 |
| March 2014 | 98.66 | 98.25 | 97.72 |
| April 2014 | 98.80 | 98.36 | 97.81 |
| May 2014 | 98.85 | 98.41 | 97.84 |
| June 2014 | 98.89 | 98.43 | 97.86 |
| July 2014 | 98.93 | 98.45 | 97.87 |
| August 2014 | 99.00 | 98.51 | 97.90 |
| September 2014 | 98.97 | 98.47 | 97.86 |
| October 2014 | 98.78 | 98.27 | 97.64 |
| November 2014 | 98.52 | 98.01 | 97.37 |
| December 2014 | 98.30 | 97.79 | 97.13 |
| January 2015 | 97.87 | 97.32 | 96.63 |
| February 2015 | 97.67 | 97.12 | 96.42 |
| March 2015 | 97.36 | 96.80 | 96.10 |
| April 2015 | 97.05 | 96.49 | 95.78 |
| May 2015 | 96.90 | 96.32 | 95.61 |
| June 2015 | 96.76 | 96.17 | 95.45 |
| July 2015 | 96.52 | 95.93 | 95.19 |
| August 2015 | 96.13 | 95.54 | 94.80 |
| September 2015 | 95.87 | 95.27 | 94.53 |
| October 2015 | 95.72 | 95.12 | 94.33 |
| November 2015 | 95.54 | 94.92 | 94.13 |
| December 2015 | 95.22 | 94.60 | 93.80 |
| January 2016 | 95.22 | 94.52 | 93.63 |
| February 2016 | 95.24 | 94.52 | 93.59 |
| March 2016 | 95.04 | 94.31 | 93.36 |
| April 2016 | 95.08 | 94.34 | 93.38 |
| May 2016 | 95.51 | 94.76 | 93.79 |
| June 2016 | 95.47 | 94.70 | 93.72 |
| July 2016 | 95.55 | 94.77 | 93.77 |
| August 2016 | 95.61 | 94.83 | 93.81 |
| September 2016 | 95.53 | 94.74 | 93.71 |
| October 2016 | 95.55 | 94.74 | 93.70 |
| November 2016 | 95.34 | 94.52 | 93.48 |
| December 2016 | 95.17 | 94.35 | 93.30 |
| January 2017 | 95.19 | 94.33 | 93.16 |
| February 2017 | 95.94 | 95.07 | 93.82 |
| March 2017 | 96.14 | 95.22 | 93.96 |
| April 2017 | 96.63 | 95.66 | 94.29 |
| May 2017 | 96.57 | 95.59 | 94.21 |
| June 2017 | 96.60 | 95.61 | 94.22 |
| July 2017 | 96.54 | 95.53 | 94.14 |
| August 2017 | 96.81 | 95.78 | 94.38 |
| September 2017 | 96.77 | 95.73 | 94.33 |
| October 2017 | 97.28 | 96.19 | 94.71 |
| November 2017 | 97.36 | 96.26 | 94.77 |
| December 2017 | 97.39 | 96.28 | 94.80 |
| January 2018 | 97.57 | 96.44 | 94.92 |
| February 2018 | 98.13 | 96.98 | 95.40 |
| March 2018 | 98.32 | 97.17 | 95.57 |
| April 2018 | 98.66 | 97.49 | 95.87 |
| May 2018 | 98.81 | 97.64 | 96.00 |
| June 2018 | 98.71 | 97.53 | 95.89 |
| July 2018 | 98.71 | 97.51 | 95.86 |
| August 2018 | 98.99 | 97.79 | 96.13 |
| September 2018 | 98.99 | 97.79 | 96.12 |
| October 2018 | 98.91 | 97.71 | 96.04 |
| November 2018 | 98.66 | 97.46 | 95.79 |
| December 2018 | 98.91 | 97.71 | 96.04 |
| January 2019 | 98.84 | 97.63 | 95.94 |
| February 2019 | 98.80 | 97.59 | 95.90 |
| March 2019 | 98.67 | 97.45 | 95.76 |
| April 2019 | 98.49 | 97.27 | 95.57 |
| May 2019 | 98.43 | 97.20 | 95.50 |
| June 2019 | 98.38 | 97.14 | 95.43 |
| July 2019 | 98.41 | 97.17 | 95.45 |
| August 2019 | 98.49 | 97.24 | 95.51 |
| September 2019 | 98.52 | 97.27 | 95.53 |
| October 2019 | 98.20 | 96.95 | 95.22 |
| November 2019 | 98.15 | 96.90 | 95.16 |
| December 2019 | 98.12 | 96.87 | 95.13 |
| January 2020 | 98.37 | 97.08 | 95.33 |
| February 2020 | 98.83 | 97.53 | 95.76 |
| March 2020 | 98.92 | 97.60 | 95.83 |
| April 2020 | 97.99 | 96.67 | 94.90 |
| May 2020 | 97.72 | 96.41 | 94.64 |
| June 2020 | 97.75 | 96.43 | 94.66 |
| July 2020 | 98.16 | 96.82 | 95.04 |
| August 2020 | 98.49 | 97.15 | 95.36 |
| September 2020 | 98.74 | 97.39 | 95.59 |
| October 2020 | 98.73 | 97.38 | 95.57 |
| November 2020 | 98.94 | 97.57 | 95.76 |
| December 2020 | 99.29 | 97.91 | 96.09 |
| January 2021 | 100.00 | 98.60 | 96.76 |
| February 2021 | 100.43 | 99.02 | 97.16 |
| March 2021 | 101.35 | 99.92 | 98.03 |
| April 2021 | 102.19 | 100.72 | 98.79 |
| May 2021 | 103.14 | 101.63 | 99.67 |
| June 2021 | 103.51 | 101.97 | 100.00 |
| July 2021 | 104.11 | 102.53 | 100.53 |
| August 2021 | 104.78 | 103.18 | 101.16 |
| September 2021 | 105.09 | 103.47 | 101.45 |
| October 2021 | 105.73 | 104.08 | 102.03 |
| November 2021 | 106.22 | 104.55 | 102.49 |
| December 2021 | 106.44 | 104.76 | 102.70 |
| January 2022 | 109.04 | 107.30 | 105.08 |
| February 2022 | 110.05 | 108.28 | 106.04 |
| March 2022 | 111.41 | 109.63 | 107.36 |
| April 2022 | 112.52 | 110.66 | 108.36 |
| May 2022 | 111.91 | 110.04 | 107.75 |
| June 2022 | 111.28 | 109.41 | 107.12 |
| July 2022 | 111.51 | 109.58 | 107.22 |
| August 2022 | 110.78 | 108.88 | 106.56 |
| September 2022 | 109.89 | 108.00 | 105.70 |
| October 2022 | 109.83 | 107.95 | 105.66 |
| November 2022 | 109.59 | 107.69 | 105.40 |
| December 2022 | 110.04 | 108.13 | 105.84 |
| Note: The chart shows our calculation of a headline import price index using the indexes that replicate at least well. The alternative lines show the impact of using a geometric Young formula at both the weight-group and classification-group levels or at only the weight-group level. Source: U.S. Bureau of Labor Statistics. | |||
| Month | Laspeyres index | Geometric index at the weight-group level | Geometric index at the weight-group and classification-group levels |
|---|---|---|---|
| January 2012 | 100.00 | 100.00 | 100.00 |
| February 2012 | 100.45 | 100.42 | 100.41 |
| March 2012 | 100.80 | 100.76 | 100.74 |
| April 2012 | 100.86 | 100.79 | 100.75 |
| May 2012 | 100.72 | 100.64 | 100.59 |
| June 2012 | 100.09 | 99.99 | 99.92 |
| July 2012 | 99.80 | 99.68 | 99.58 |
| August 2012 | 100.00 | 99.86 | 99.75 |
| September 2012 | 100.36 | 100.20 | 100.08 |
| October 2012 | 100.90 | 100.71 | 100.57 |
| November 2012 | 100.69 | 100.48 | 100.32 |
| December 2012 | 100.64 | 100.41 | 100.25 |
| January 2013 | 100.98 | 100.72 | 100.51 |
| February 2013 | 101.39 | 101.10 | 100.87 |
| March 2013 | 101.16 | 100.84 | 100.61 |
| April 2013 | 100.88 | 100.53 | 100.28 |
| May 2013 | 100.28 | 99.92 | 99.66 |
| June 2013 | 100.06 | 99.69 | 99.42 |
| July 2013 | 99.74 | 99.35 | 99.07 |
| August 2013 | 99.44 | 99.03 | 98.73 |
| September 2013 | 99.71 | 99.28 | 98.97 |
| October 2013 | 99.46 | 99.01 | 98.70 |
| November 2013 | 99.32 | 98.87 | 98.55 |
| December 2013 | 99.13 | 98.67 | 98.34 |
| January 2014 | 99.17 | 98.66 | 98.30 |
| February 2014 | 99.39 | 98.87 | 98.49 |
| March 2014 | 99.64 | 99.10 | 98.71 |
| April 2014 | 99.80 | 99.25 | 98.84 |
| May 2014 | 99.66 | 99.09 | 98.68 |
| June 2014 | 99.52 | 98.93 | 98.50 |
| July 2014 | 99.67 | 99.06 | 98.61 |
| August 2014 | 99.63 | 99.00 | 98.54 |
| September 2014 | 99.40 | 98.76 | 98.29 |
| October 2014 | 98.74 | 98.09 | 97.61 |
| November 2014 | 98.10 | 97.44 | 96.96 |
| December 2014 | 97.99 | 97.31 | 96.80 |
| January 2015 | 97.53 | 96.78 | 96.25 |
| February 2015 | 97.42 | 96.66 | 96.11 |
| March 2015 | 97.19 | 96.40 | 95.84 |
| April 2015 | 97.03 | 96.19 | 95.62 |
| May 2015 | 96.83 | 95.98 | 95.40 |
| June 2015 | 96.80 | 95.91 | 95.32 |
| July 2015 | 96.42 | 95.54 | 94.93 |
| August 2015 | 95.67 | 94.79 | 94.17 |
| September 2015 | 95.40 | 94.50 | 93.89 |
| October 2015 | 95.16 | 94.25 | 93.63 |
| November 2015 | 94.51 | 93.60 | 92.97 |
| December 2015 | 94.11 | 93.17 | 92.55 |
| January 2016 | 93.78 | 92.81 | 92.14 |
| February 2016 | 93.67 | 92.67 | 91.99 |
| March 2016 | 93.62 | 92.62 | 91.90 |
| April 2016 | 93.75 | 92.73 | 92.00 |
| May 2016 | 94.14 | 93.09 | 92.33 |
| June 2016 | 94.09 | 93.04 | 92.24 |
| July 2016 | 94.38 | 93.29 | 92.47 |
| August 2016 | 94.14 | 93.04 | 92.20 |
| September 2016 | 94.04 | 92.93 | 92.09 |
| October 2016 | 93.97 | 92.83 | 91.97 |
| November 2016 | 94.04 | 92.88 | 92.01 |
| December 2016 | 93.87 | 92.69 | 91.81 |
| January 2017 | 93.88 | 92.61 | 91.70 |
| February 2017 | 94.20 | 92.90 | 91.98 |
| March 2017 | 94.34 | 93.01 | 92.08 |
| April 2017 | 94.64 | 93.26 | 92.31 |
| May 2017 | 94.58 | 93.18 | 92.22 |
| June 2017 | 94.59 | 93.18 | 92.21 |
| July 2017 | 94.59 | 93.18 | 92.20 |
| August 2017 | 94.90 | 93.47 | 92.48 |
| September 2017 | 95.33 | 93.87 | 92.85 |
| October 2017 | 95.62 | 94.12 | 93.08 |
| November 2017 | 95.67 | 94.15 | 93.10 |
| December 2017 | 95.83 | 94.27 | 93.21 |
| January 2018 | 95.95 | 94.30 | 93.20 |
| February 2018 | 96.40 | 94.71 | 93.59 |
| March 2018 | 96.68 | 94.97 | 93.81 |
| April 2018 | 97.05 | 95.27 | 94.08 |
| May 2018 | 97.32 | 95.51 | 94.29 |
| June 2018 | 97.35 | 95.54 | 94.30 |
| July 2018 | 97.27 | 95.46 | 94.23 |
| August 2018 | 97.15 | 95.34 | 94.11 |
| September 2018 | 97.07 | 95.25 | 94.03 |
| October 2018 | 97.06 | 95.25 | 94.02 |
| November 2018 | 96.96 | 95.14 | 93.91 |
| December 2018 | 96.75 | 94.92 | 93.70 |
| January 2019 | 97.16 | 95.30 | 94.05 |
| February 2019 | 97.71 | 95.80 | 94.54 |
| March 2019 | 97.69 | 95.77 | 94.51 |
| April 2019 | 97.96 | 96.02 | 94.74 |
| May 2019 | 97.76 | 95.81 | 94.53 |
| June 2019 | 97.66 | 95.71 | 94.43 |
| July 2019 | 97.44 | 95.50 | 94.21 |
| August 2019 | 97.27 | 95.31 | 94.04 |
| September 2019 | 97.02 | 95.07 | 93.80 |
| October 2019 | 96.89 | 94.93 | 93.65 |
| November 2019 | 97.04 | 95.07 | 93.78 |
| December 2019 | 96.98 | 95.00 | 93.70 |
| January 2020 | 97.14 | 95.19 | 93.87 |
| February 2020 | 97.35 | 95.39 | 94.07 |
| March 2020 | 97.26 | 95.31 | 93.99 |
| April 2020 | 96.94 | 94.97 | 93.65 |
| May 2020 | 96.58 | 94.59 | 93.27 |
| June 2020 | 96.62 | 94.60 | 93.28 |
| July 2020 | 96.85 | 94.82 | 93.48 |
| August 2020 | 97.28 | 95.22 | 93.83 |
| September 2020 | 97.80 | 95.71 | 94.27 |
| October 2020 | 98.55 | 96.42 | 94.95 |
| November 2020 | 98.77 | 96.63 | 95.14 |
| December 2020 | 99.53 | 97.38 | 95.83 |
| January 2021 | 101.42 | 99.13 | 97.51 |
| February 2021 | 102.61 | 100.23 | 98.50 |
| March 2021 | 105.11 | 102.56 | 100.67 |
| April 2021 | 106.99 | 104.33 | 102.30 |
| May 2021 | 108.67 | 106.00 | 103.85 |
| June 2021 | 108.71 | 106.02 | 103.86 |
| July 2021 | 108.76 | 105.98 | 103.83 |
| August 2021 | 108.74 | 105.96 | 103.86 |
| September 2021 | 108.39 | 105.54 | 103.47 |
| October 2021 | 110.17 | 107.28 | 105.20 |
| November 2021 | 110.40 | 107.52 | 105.46 |
| December 2021 | 110.41 | 107.51 | 105.47 |
| January 2022 | 111.52 | 108.61 | 106.55 |
| February 2022 | 112.50 | 109.58 | 107.54 |
| March 2022 | 115.73 | 112.74 | 110.68 |
| April 2022 | 117.89 | 114.78 | 112.66 |
| May 2022 | 117.90 | 114.76 | 112.59 |
| June 2022 | 116.86 | 113.73 | 111.62 |
| July 2022 | 116.58 | 113.43 | 111.28 |
| August 2022 | 116.93 | 113.79 | 111.68 |
| September 2022 | 115.36 | 112.18 | 110.12 |
| October 2022 | 116.06 | 112.81 | 110.67 |
| November 2022 | 115.49 | 112.26 | 110.17 |
| December 2022 | 114.69 | 111.49 | 109.46 |
| Note: The chart shows our calculation of a headline export price index using the indexes that replicate at least well. The alternative lines show the impact of using a geometric Young formula at both the weight-group and classification-group levels or at only the weight-group level. Source: U.S. Bureau of Labor Statistics. | |||
We find that the impact of the geometric Young formula varies substantially across four-digit HS indexes. Chart 5 shows that 72 of the four-digit HS indexes change less than 0.1 percentage point per year, on average, when calculated with the geometric Young method through the classification group. Another 80 indexes have average changes between 0.1 and 0.3 percentage point per year. However, 53 indexes have average changes in excess of 0.5 percentage point per year.14
| Percentage-point difference | Count |
|---|---|
| 0.0 | 5 |
| ≤ 0.1 | 67 |
| 0.2 | 45 |
| 0.3 | 35 |
| 0.4 | 20 |
| 0.5 | 12 |
| 0.6 | 11 |
| 0.7 | 7 |
| 0.8 | 8 |
| 0.9 | 5 |
| > 0.9 | 22 |
| Note: The chart shows the number of four-digit Harmonized System indexes with an average annual difference in a given percentage-point bin of 0.1. The difference is a Laspeyres formula calculation minus a geometric Young formula calculation. For example, the 0.4 bin represents indexes with an average annual difference above 0.3 percentage point but less than or equal to 0.4 percentage point. Source: U.S. Bureau of Labor Statistics. | |
We decompose the effects of using the geometric mean to calculate the indexes into the two following components: a change in the calculation of the weight group and a change in the calculation of the classification group. We do this for two reasons. First, it may make sense to use the geometric Young formula at the weight-group level and the Laspeyres formula at the classification-group level. Each weight group reflects trade of similar items within a company. Thus, the goods within a weight group will be more substitutable than goods within a classification group. Therefore, the economic case to use the geometric Young formula is strong at the weight-group level. Second, the decomposition of effects improves our understanding of the impacts at the classification-group level. Many weight groups have only one item; thereby, the choice of formula does not matter. As an extreme case, all of the impact of using a geometric mean could appear when weight groups are aggregated to classification groups. In that case, it might not be worth expending additional resources to study or change the methods used to aggregate items to the weight-group level.
In our study, we find smaller impacts for imports than exports at the weight-group level. In fact, the mean difference of 0.163 percentage point for the imports index is about two-thirds of the mean difference of 0.268 for the exports index. (See table 1).
| Index | Weight group only, mean difference | Weight group only, median difference | Classification and weight groups, mean difference | Classification and weight groups, median difference |
|---|---|---|---|---|
| Imports | 0.163 | 0.169 | 0.373 | 0.414 |
| Exports | 0.268 | 0.264 | 0.462 | 0.452 |
| Source: U.S. Bureau of Labor Statistics. | ||||
It is difficult to determine exactly why the geometric Young formula has a larger impact on the estimation of export indexes, but one possible cause is that import weight groups are more likely to contain only one item. About 53 percent of import weight groups have only one item, while about 45 percent of export weight groups have only one item. When a weight group has one item, there is no difference between an arithmetic or geometric mean. Similarly, less than 10 percent of import weight groups have more than five items, but more than 13 percent of export weight groups have more than five items. At the classification-group level, imports and exports have similar numbers of weight groups.
Over time, the number of weight groups with only one item has increased, especially for imports, while the number of weight groups with more than five items has decreased. (See charts 6 and 7.) If this decline continues, the impact of switching to the geometric Young formula will carry less significance over time. Another circumstance that may change these results are when the MXPIs begin to use administrative data in 2025 for about one-third of trade.15 (For more details about this change, see appendix.) We find that the effects of using the geometric Young formula to calculate MXPIs would not meaningfully change estimates if administrative data are used.
| Month | 1 item | 2 items | 3 items | 4 items | 5 or more items |
|---|---|---|---|---|---|
| February 2012 | 0.300 | 0.174 | 0.184 | 0.109 | 0.233 |
| March 2012 | 0.311 | 0.179 | 0.168 | 0.111 | 0.231 |
| April 2012 | 0.294 | 0.173 | 0.157 | 0.117 | 0.259 |
| May 2012 | 0.307 | 0.170 | 0.163 | 0.107 | 0.252 |
| June 2012 | 0.304 | 0.171 | 0.172 | 0.111 | 0.242 |
| July 2012 | 0.309 | 0.191 | 0.150 | 0.113 | 0.237 |
| August 2012 | 0.317 | 0.167 | 0.163 | 0.119 | 0.234 |
| September 2012 | 0.299 | 0.172 | 0.182 | 0.109 | 0.239 |
| October 2012 | 0.305 | 0.176 | 0.165 | 0.116 | 0.238 |
| November 2012 | 0.307 | 0.174 | 0.144 | 0.129 | 0.245 |
| December 2012 | 0.309 | 0.181 | 0.173 | 0.120 | 0.217 |
| January 2013 | 0.329 | 0.166 | 0.156 | 0.121 | 0.228 |
| February 2013 | 0.330 | 0.165 | 0.163 | 0.109 | 0.233 |
| March 2013 | 0.319 | 0.171 | 0.157 | 0.117 | 0.236 |
| April 2013 | 0.327 | 0.166 | 0.144 | 0.119 | 0.244 |
| May 2013 | 0.342 | 0.155 | 0.142 | 0.115 | 0.247 |
| June 2013 | 0.325 | 0.162 | 0.148 | 0.121 | 0.243 |
| July 2013 | 0.306 | 0.163 | 0.155 | 0.123 | 0.252 |
| August 2013 | 0.320 | 0.182 | 0.132 | 0.119 | 0.247 |
| September 2013 | 0.313 | 0.171 | 0.143 | 0.123 | 0.250 |
| October 2013 | 0.318 | 0.165 | 0.143 | 0.125 | 0.249 |
| November 2013 | 0.319 | 0.167 | 0.145 | 0.122 | 0.247 |
| December 2013 | 0.313 | 0.169 | 0.146 | 0.126 | 0.246 |
| January 2014 | 0.342 | 0.161 | 0.140 | 0.127 | 0.230 |
| February 2014 | 0.343 | 0.168 | 0.136 | 0.127 | 0.226 |
| March 2014 | 0.347 | 0.167 | 0.134 | 0.124 | 0.228 |
| April 2014 | 0.352 | 0.184 | 0.111 | 0.125 | 0.228 |
| May 2014 | 0.351 | 0.158 | 0.135 | 0.125 | 0.231 |
| June 2014 | 0.348 | 0.160 | 0.131 | 0.123 | 0.238 |
| July 2014 | 0.357 | 0.165 | 0.130 | 0.129 | 0.218 |
| August 2014 | 0.339 | 0.157 | 0.142 | 0.134 | 0.228 |
| September 2014 | 0.348 | 0.174 | 0.136 | 0.125 | 0.217 |
| October 2014 | 0.335 | 0.174 | 0.128 | 0.117 | 0.246 |
| November 2014 | 0.345 | 0.164 | 0.130 | 0.121 | 0.239 |
| December 2014 | 0.345 | 0.169 | 0.131 | 0.115 | 0.240 |
| January 2015 | 0.358 | 0.164 | 0.139 | 0.130 | 0.209 |
| February 2015 | 0.332 | 0.168 | 0.156 | 0.111 | 0.233 |
| March 2015 | 0.333 | 0.168 | 0.148 | 0.119 | 0.231 |
| April 2015 | 0.307 | 0.175 | 0.139 | 0.143 | 0.236 |
| May 2015 | 0.335 | 0.154 | 0.138 | 0.129 | 0.243 |
| June 2015 | 0.330 | 0.159 | 0.143 | 0.127 | 0.240 |
| July 2015 | 0.334 | 0.164 | 0.137 | 0.137 | 0.228 |
| August 2015 | 0.342 | 0.153 | 0.134 | 0.134 | 0.237 |
| September 2015 | 0.346 | 0.150 | 0.144 | 0.139 | 0.222 |
| October 2015 | 0.344 | 0.159 | 0.133 | 0.137 | 0.227 |
| November 2015 | 0.329 | 0.158 | 0.150 | 0.140 | 0.221 |
| December 2015 | 0.330 | 0.153 | 0.150 | 0.130 | 0.236 |
| January 2016 | 0.308 | 0.167 | 0.163 | 0.137 | 0.224 |
| February 2016 | 0.297 | 0.172 | 0.149 | 0.150 | 0.233 |
| March 2016 | 0.320 | 0.151 | 0.152 | 0.142 | 0.236 |
| April 2016 | 0.318 | 0.147 | 0.162 | 0.131 | 0.243 |
| May 2016 | 0.310 | 0.147 | 0.147 | 0.145 | 0.250 |
| June 2016 | 0.323 | 0.146 | 0.150 | 0.132 | 0.248 |
| July 2016 | 0.322 | 0.161 | 0.162 | 0.116 | 0.238 |
| August 2016 | 0.313 | 0.155 | 0.153 | 0.125 | 0.253 |
| September 2016 | 0.323 | 0.142 | 0.113 | 0.163 | 0.259 |
| October 2016 | 0.307 | 0.164 | 0.113 | 0.164 | 0.252 |
| November 2016 | 0.314 | 0.156 | 0.121 | 0.164 | 0.245 |
| December 2016 | 0.316 | 0.161 | 0.125 | 0.170 | 0.228 |
| January 2017 | 0.298 | 0.171 | 0.104 | 0.173 | 0.255 |
| February 2017 | 0.312 | 0.147 | 0.124 | 0.178 | 0.237 |
| March 2017 | 0.313 | 0.141 | 0.126 | 0.158 | 0.262 |
| April 2017 | 0.309 | 0.162 | 0.119 | 0.164 | 0.246 |
| May 2017 | 0.297 | 0.147 | 0.134 | 0.161 | 0.261 |
| June 2017 | 0.294 | 0.147 | 0.137 | 0.161 | 0.262 |
| July 2017 | 0.300 | 0.143 | 0.123 | 0.177 | 0.257 |
| August 2017 | 0.301 | 0.135 | 0.131 | 0.185 | 0.247 |
| September 2017 | 0.340 | 0.128 | 0.093 | 0.180 | 0.260 |
| October 2017 | 0.285 | 0.144 | 0.137 | 0.178 | 0.256 |
| November 2017 | 0.305 | 0.140 | 0.135 | 0.163 | 0.257 |
| December 2017 | 0.315 | 0.148 | 0.100 | 0.177 | 0.259 |
| January 2018 | 0.293 | 0.125 | 0.099 | 0.181 | 0.302 |
| February 2018 | 0.299 | 0.140 | 0.086 | 0.152 | 0.323 |
| March 2018 | 0.277 | 0.135 | 0.095 | 0.142 | 0.351 |
| April 2018 | 0.288 | 0.134 | 0.092 | 0.156 | 0.330 |
| May 2018 | 0.283 | 0.134 | 0.104 | 0.158 | 0.320 |
| June 2018 | 0.263 | 0.149 | 0.101 | 0.161 | 0.326 |
| July 2018 | 0.263 | 0.139 | 0.098 | 0.163 | 0.336 |
| August 2018 | 0.265 | 0.147 | 0.098 | 0.168 | 0.322 |
| September 2018 | 0.260 | 0.142 | 0.096 | 0.164 | 0.338 |
| October 2018 | 0.258 | 0.152 | 0.110 | 0.157 | 0.323 |
| November 2018 | 0.262 | 0.144 | 0.106 | 0.157 | 0.331 |
| December 2018 | 0.282 | 0.132 | 0.101 | 0.156 | 0.329 |
| January 2019 | 0.258 | 0.149 | 0.134 | 0.166 | 0.293 |
| February 2019 | 0.262 | 0.162 | 0.115 | 0.161 | 0.299 |
| March 2019 | 0.266 | 0.148 | 0.106 | 0.171 | 0.310 |
| April 2019 | 0.262 | 0.179 | 0.099 | 0.164 | 0.296 |
| May 2019 | 0.295 | 0.150 | 0.118 | 0.171 | 0.266 |
| June 2019 | 0.276 | 0.165 | 0.113 | 0.163 | 0.283 |
| July 2019 | 0.297 | 0.157 | 0.106 | 0.164 | 0.276 |
| August 2019 | 0.316 | 0.169 | 0.105 | 0.163 | 0.247 |
| September 2019 | 0.292 | 0.135 | 0.111 | 0.182 | 0.280 |
| October 2019 | 0.295 | 0.167 | 0.105 | 0.146 | 0.287 |
| November 2019 | 0.307 | 0.136 | 0.120 | 0.150 | 0.286 |
| December 2019 | 0.286 | 0.158 | 0.113 | 0.180 | 0.263 |
| January 2020 | 0.320 | 0.139 | 0.119 | 0.153 | 0.269 |
| February 2020 | 0.297 | 0.148 | 0.141 | 0.164 | 0.249 |
| March 2020 | 0.275 | 0.142 | 0.149 | 0.169 | 0.265 |
| April 2020 | 0.291 | 0.148 | 0.144 | 0.155 | 0.262 |
| May 2020 | 0.304 | 0.135 | 0.152 | 0.152 | 0.257 |
| June 2020 | 0.268 | 0.158 | 0.155 | 0.154 | 0.265 |
| July 2020 | 0.298 | 0.152 | 0.139 | 0.148 | 0.263 |
| August 2020 | 0.285 | 0.186 | 0.158 | 0.144 | 0.228 |
| September 2020 | 0.281 | 0.196 | 0.155 | 0.142 | 0.227 |
| October 2020 | 0.284 | 0.182 | 0.162 | 0.135 | 0.237 |
| November 2020 | 0.269 | 0.191 | 0.170 | 0.137 | 0.234 |
| December 2020 | 0.288 | 0.181 | 0.177 | 0.150 | 0.203 |
| January 2021 | 0.358 | 0.149 | 0.175 | 0.122 | 0.196 |
| February 2021 | 0.322 | 0.177 | 0.167 | 0.128 | 0.206 |
| March 2021 | 0.330 | 0.170 | 0.156 | 0.142 | 0.202 |
| April 2021 | 0.339 | 0.150 | 0.169 | 0.140 | 0.202 |
| May 2021 | 0.362 | 0.162 | 0.151 | 0.147 | 0.177 |
| June 2021 | 0.334 | 0.172 | 0.167 | 0.140 | 0.188 |
| July 2021 | 0.365 | 0.135 | 0.171 | 0.150 | 0.179 |
| August 2021 | 0.350 | 0.161 | 0.160 | 0.139 | 0.190 |
| September 2021 | 0.346 | 0.147 | 0.174 | 0.138 | 0.195 |
| October 2021 | 0.366 | 0.139 | 0.160 | 0.134 | 0.201 |
| November 2021 | 0.395 | 0.119 | 0.168 | 0.131 | 0.186 |
| December 2021 | 0.362 | 0.146 | 0.170 | 0.131 | 0.190 |
| January 2022 | 0.365 | 0.142 | 0.163 | 0.115 | 0.216 |
| February 2022 | 0.393 | 0.124 | 0.147 | 0.113 | 0.222 |
| March 2022 | 0.382 | 0.130 | 0.158 | 0.110 | 0.220 |
| April 2022 | 0.344 | 0.161 | 0.163 | 0.080 | 0.252 |
| May 2022 | 0.324 | 0.184 | 0.160 | 0.092 | 0.241 |
| June 2022 | 0.326 | 0.203 | 0.157 | 0.099 | 0.216 |
| July 2022 | 0.367 | 0.189 | 0.148 | 0.070 | 0.226 |
| August 2022 | 0.379 | 0.211 | 0.109 | 0.079 | 0.222 |
| September 2022 | 0.343 | 0.269 | 0.097 | 0.085 | 0.206 |
| October 2022 | 0.401 | 0.225 | 0.089 | 0.062 | 0.223 |
| November 2022 | 0.392 | 0.193 | 0.079 | 0.072 | 0.265 |
| December 2022 | 0.367 | 0.256 | 0.091 | 0.082 | 0.204 |
| Note: The chart shows the proportion of headline-export-index weight corresponding to weight groups with a given item count over time. For example, in February 2012, the headline export index had 30.0 percent of its total weight composed of weight groups with only one item. Source: U.S. Bureau of Labor Statistics. | |||||
| Month | 1 item | 2 items | 3 items | 4 items | 5 or more items |
|---|---|---|---|---|---|
| February 2012 | 0.376 | 0.199 | 0.130 | 0.101 | 0.194 |
| March 2012 | 0.384 | 0.200 | 0.131 | 0.093 | 0.197 |
| April 2012 | 0.369 | 0.189 | 0.120 | 0.097 | 0.224 |
| May 2012 | 0.397 | 0.192 | 0.130 | 0.085 | 0.202 |
| June 2012 | 0.379 | 0.185 | 0.136 | 0.090 | 0.210 |
| July 2012 | 0.384 | 0.221 | 0.120 | 0.076 | 0.199 |
| August 2012 | 0.367 | 0.204 | 0.149 | 0.080 | 0.200 |
| September 2012 | 0.395 | 0.172 | 0.145 | 0.080 | 0.215 |
| October 2012 | 0.390 | 0.166 | 0.145 | 0.087 | 0.213 |
| November 2012 | 0.388 | 0.183 | 0.155 | 0.075 | 0.199 |
| December 2012 | 0.382 | 0.164 | 0.156 | 0.092 | 0.206 |
| January 2013 | 0.370 | 0.198 | 0.118 | 0.082 | 0.229 |
| February 2013 | 0.389 | 0.190 | 0.120 | 0.097 | 0.206 |
| March 2013 | 0.390 | 0.174 | 0.131 | 0.103 | 0.202 |
| April 2013 | 0.398 | 0.171 | 0.117 | 0.137 | 0.177 |
| May 2013 | 0.409 | 0.191 | 0.115 | 0.101 | 0.184 |
| June 2013 | 0.401 | 0.184 | 0.135 | 0.100 | 0.180 |
| July 2013 | 0.404 | 0.178 | 0.110 | 0.105 | 0.208 |
| August 2013 | 0.406 | 0.179 | 0.126 | 0.119 | 0.170 |
| September 2013 | 0.393 | 0.178 | 0.135 | 0.117 | 0.176 |
| October 2013 | 0.393 | 0.195 | 0.132 | 0.106 | 0.175 |
| November 2013 | 0.390 | 0.214 | 0.128 | 0.096 | 0.172 |
| December 2013 | 0.391 | 0.202 | 0.127 | 0.118 | 0.162 |
| January 2014 | 0.389 | 0.200 | 0.108 | 0.107 | 0.196 |
| February 2014 | 0.397 | 0.198 | 0.137 | 0.091 | 0.177 |
| March 2014 | 0.400 | 0.188 | 0.150 | 0.090 | 0.172 |
| April 2014 | 0.393 | 0.215 | 0.130 | 0.104 | 0.158 |
| May 2014 | 0.395 | 0.217 | 0.141 | 0.101 | 0.146 |
| June 2014 | 0.384 | 0.216 | 0.146 | 0.108 | 0.146 |
| July 2014 | 0.378 | 0.199 | 0.159 | 0.107 | 0.157 |
| August 2014 | 0.410 | 0.190 | 0.144 | 0.099 | 0.157 |
| September 2014 | 0.417 | 0.186 | 0.139 | 0.106 | 0.152 |
| October 2014 | 0.420 | 0.183 | 0.138 | 0.107 | 0.151 |
| November 2014 | 0.409 | 0.188 | 0.144 | 0.104 | 0.156 |
| December 2014 | 0.385 | 0.219 | 0.126 | 0.117 | 0.153 |
| January 2015 | 0.384 | 0.205 | 0.139 | 0.094 | 0.178 |
| February 2015 | 0.352 | 0.216 | 0.169 | 0.087 | 0.175 |
| March 2015 | 0.356 | 0.184 | 0.157 | 0.132 | 0.170 |
| April 2015 | 0.365 | 0.208 | 0.136 | 0.122 | 0.169 |
| May 2015 | 0.355 | 0.219 | 0.137 | 0.119 | 0.170 |
| June 2015 | 0.363 | 0.203 | 0.156 | 0.118 | 0.160 |
| July 2015 | 0.353 | 0.218 | 0.132 | 0.120 | 0.178 |
| August 2015 | 0.360 | 0.230 | 0.129 | 0.108 | 0.174 |
| September 2015 | 0.363 | 0.223 | 0.127 | 0.111 | 0.176 |
| October 2015 | 0.342 | 0.190 | 0.153 | 0.109 | 0.206 |
| November 2015 | 0.356 | 0.194 | 0.145 | 0.114 | 0.191 |
| December 2015 | 0.351 | 0.195 | 0.142 | 0.129 | 0.183 |
| January 2016 | 0.356 | 0.191 | 0.142 | 0.118 | 0.193 |
| February 2016 | 0.350 | 0.218 | 0.134 | 0.127 | 0.171 |
| March 2016 | 0.383 | 0.200 | 0.138 | 0.119 | 0.167 |
| April 2016 | 0.360 | 0.228 | 0.124 | 0.114 | 0.174 |
| May 2016 | 0.363 | 0.224 | 0.159 | 0.094 | 0.160 |
| June 2016 | 0.355 | 0.198 | 0.154 | 0.123 | 0.171 |
| July 2016 | 0.346 | 0.237 | 0.123 | 0.113 | 0.181 |
| August 2016 | 0.362 | 0.227 | 0.127 | 0.108 | 0.177 |
| September 2016 | 0.335 | 0.228 | 0.125 | 0.135 | 0.177 |
| October 2016 | 0.336 | 0.233 | 0.155 | 0.091 | 0.185 |
| November 2016 | 0.345 | 0.223 | 0.127 | 0.124 | 0.180 |
| December 2016 | 0.348 | 0.205 | 0.127 | 0.134 | 0.186 |
| January 2017 | 0.418 | 0.186 | 0.120 | 0.107 | 0.169 |
| February 2017 | 0.387 | 0.179 | 0.115 | 0.117 | 0.202 |
| March 2017 | 0.346 | 0.200 | 0.115 | 0.153 | 0.186 |
| April 2017 | 0.396 | 0.191 | 0.114 | 0.124 | 0.175 |
| May 2017 | 0.389 | 0.181 | 0.118 | 0.115 | 0.196 |
| June 2017 | 0.386 | 0.173 | 0.101 | 0.155 | 0.185 |
| July 2017 | 0.370 | 0.211 | 0.108 | 0.105 | 0.205 |
| August 2017 | 0.353 | 0.220 | 0.100 | 0.082 | 0.245 |
| September 2017 | 0.373 | 0.197 | 0.126 | 0.109 | 0.194 |
| October 2017 | 0.382 | 0.210 | 0.122 | 0.088 | 0.197 |
| November 2017 | 0.360 | 0.210 | 0.150 | 0.103 | 0.177 |
| December 2017 | 0.351 | 0.205 | 0.109 | 0.102 | 0.232 |
| January 2018 | 0.362 | 0.179 | 0.138 | 0.095 | 0.225 |
| February 2018 | 0.343 | 0.174 | 0.201 | 0.077 | 0.206 |
| March 2018 | 0.324 | 0.190 | 0.188 | 0.086 | 0.211 |
| April 2018 | 0.369 | 0.180 | 0.133 | 0.094 | 0.225 |
| May 2018 | 0.381 | 0.177 | 0.133 | 0.084 | 0.225 |
| June 2018 | 0.391 | 0.184 | 0.116 | 0.087 | 0.222 |
| July 2018 | 0.384 | 0.201 | 0.099 | 0.099 | 0.217 |
| August 2018 | 0.338 | 0.190 | 0.184 | 0.087 | 0.202 |
| September 2018 | 0.397 | 0.196 | 0.097 | 0.107 | 0.203 |
| October 2018 | 0.389 | 0.187 | 0.112 | 0.108 | 0.203 |
| November 2018 | 0.392 | 0.185 | 0.117 | 0.093 | 0.213 |
| December 2018 | 0.449 | 0.172 | 0.099 | 0.096 | 0.184 |
| January 2019 | 0.383 | 0.182 | 0.125 | 0.089 | 0.221 |
| February 2019 | 0.364 | 0.176 | 0.116 | 0.102 | 0.241 |
| March 2019 | 0.357 | 0.208 | 0.112 | 0.101 | 0.221 |
| April 2019 | 0.370 | 0.202 | 0.113 | 0.106 | 0.210 |
| May 2019 | 0.383 | 0.192 | 0.114 | 0.087 | 0.224 |
| June 2019 | 0.379 | 0.189 | 0.116 | 0.105 | 0.212 |
| July 2019 | 0.372 | 0.209 | 0.114 | 0.089 | 0.215 |
| August 2019 | 0.362 | 0.197 | 0.115 | 0.091 | 0.235 |
| September 2019 | 0.366 | 0.204 | 0.121 | 0.089 | 0.220 |
| October 2019 | 0.387 | 0.202 | 0.116 | 0.081 | 0.215 |
| November 2019 | 0.385 | 0.196 | 0.114 | 0.080 | 0.225 |
| December 2019 | 0.401 | 0.187 | 0.115 | 0.084 | 0.213 |
| January 2020 | 0.413 | 0.191 | 0.129 | 0.076 | 0.191 |
| February 2020 | 0.402 | 0.193 | 0.123 | 0.080 | 0.203 |
| March 2020 | 0.432 | 0.195 | 0.107 | 0.089 | 0.177 |
| April 2020 | 0.417 | 0.219 | 0.109 | 0.090 | 0.165 |
| May 2020 | 0.405 | 0.198 | 0.110 | 0.084 | 0.203 |
| June 2020 | 0.400 | 0.196 | 0.109 | 0.108 | 0.187 |
| July 2020 | 0.433 | 0.194 | 0.097 | 0.089 | 0.186 |
| August 2020 | 0.415 | 0.187 | 0.096 | 0.102 | 0.200 |
| September 2020 | 0.433 | 0.203 | 0.084 | 0.093 | 0.187 |
| October 2020 | 0.413 | 0.205 | 0.090 | 0.104 | 0.189 |
| November 2020 | 0.417 | 0.188 | 0.097 | 0.091 | 0.207 |
| December 2020 | 0.401 | 0.211 | 0.105 | 0.098 | 0.186 |
| January 2021 | 0.487 | 0.175 | 0.097 | 0.078 | 0.164 |
| February 2021 | 0.395 | 0.201 | 0.093 | 0.089 | 0.221 |
| March 2021 | 0.399 | 0.230 | 0.086 | 0.074 | 0.211 |
| April 2021 | 0.402 | 0.211 | 0.085 | 0.081 | 0.221 |
| May 2021 | 0.397 | 0.216 | 0.085 | 0.082 | 0.220 |
| June 2021 | 0.385 | 0.234 | 0.084 | 0.086 | 0.211 |
| July 2021 | 0.431 | 0.201 | 0.080 | 0.083 | 0.206 |
| August 2021 | 0.428 | 0.217 | 0.082 | 0.077 | 0.197 |
| September 2021 | 0.446 | 0.218 | 0.089 | 0.061 | 0.187 |
| October 2021 | 0.458 | 0.218 | 0.082 | 0.066 | 0.175 |
| November 2021 | 0.484 | 0.156 | 0.108 | 0.067 | 0.185 |
| December 2021 | 0.466 | 0.204 | 0.115 | 0.035 | 0.180 |
| January 2022 | 0.555 | 0.138 | 0.118 | 0.033 | 0.156 |
| February 2022 | 0.554 | 0.149 | 0.130 | 0.019 | 0.148 |
| March 2022 | 0.600 | 0.161 | 0.110 | 0.021 | 0.109 |
| April 2022 | 0.583 | 0.175 | 0.129 | 0.022 | 0.092 |
| May 2022 | 0.595 | 0.184 | 0.102 | 0.017 | 0.101 |
| June 2022 | 0.637 | 0.143 | 0.105 | 0.029 | 0.087 |
| July 2022 | 0.639 | 0.166 | 0.075 | 0.033 | 0.088 |
| August 2022 | 0.572 | 0.172 | 0.102 | 0.043 | 0.110 |
| September 2022 | 0.597 | 0.212 | 0.071 | 0.045 | 0.076 |
| October 2022 | 0.574 | 0.223 | 0.049 | 0.047 | 0.107 |
| November 2022 | 0.580 | 0.219 | 0.059 | 0.096 | 0.045 |
| December 2022 | 0.587 | 0.201 | 0.062 | 0.096 | 0.054 |
| Note: The chart shows the proportion of headline-import-index weight corresponding to weight groups with a given item count over time. For example, in February 2012, the headline import index had 37.6 percent of its total weight composed of weight groups with only one item. Source: U.S. Bureau of Labor Statistics. | |||||
Our final exercise is to calculate a real trade deficit by using the geometric indexes that we calculated to deflate imports and exports. This exercise allows us to see how changes to import and export price indexes interact. Because the geometric indexes are lower for both imports and exports, the impact on the trade deficit is expected to be small. However, the United States imports more than it exports, so any change to deflators has a bigger impact on imports in terms of dollar value. Yet, geometric indexes for imports saw smaller declines than for exports in the study period. We calculate a back-of-the-envelope change to the trade deficit by combining our headline deflator series with total trade values. The actual deflating of indexes is first done at lower levels and then the real values are aggregated. Nevertheless, our exercise should provide a rough approximation of the impact.
We find that the trade deficit would be larger by about 2 percentage points. Table 2 shows the dollar-value difference between our calculation of headline import and export indexes deflated with either our calculation of Laspeyres or geometric indexes. The differences are smaller initially, but they settle at about 2 percentage points, which corresponds to about $20 billion (in 2012 U.S. dollars). This difference is relatively minor and has been stable for the last 5 years of our sample. Given these observations, we conclude that trade price indexes calculated with the geometric Young formula would not materially affect our understanding of the trade deficit.
| Year | Difference in billions of 2012 U.S. dollars | Difference in percentage points |
|---|---|---|
| 2012 | 0.0 | 0.0 |
| 2013 | 3.9 | 0.6 |
| 2014 | 5.6 | 0.8 |
| 2015 | 5.7 | 0.8 |
| 2016 | 8.4 | 1.1 |
| 2017 | 17.0 | 2.2 |
| 2018 | 17.0 | 2.0 |
| 2019 | 17.1 | 2.0 |
| 2020 | 18.9 | 2.1 |
| 2021 | 17.7 | 1.7 |
| 2022 | 25.2 | 2.2 |
| Source: U.S. Bureau of Labor Statistics. | ||
Using the geometric Young formula up to the elementary aggregate index level would increase the consistency of methods used to calculate price indexes produced by BLS. We find that switching to the geometric Young formula would have a moderate downward effect on both import and export price indexes (0.37 and 0.46 percentage point, respectively, per year). This downward impact is consistent with previous research on the geometric Young formula.16 The use of the geometric Young formula is expected to have an impact on calculated inflation, and this use will affect the calculation of the real growth of imports and exports. This specific analysis suggests that using the geometric Young formula in the calculation of MXPIs would shrink the overall trade deficit because the decline in export price indexes is larger than the decline in import price indexes.
In this appendix, we discuss our methods, consider additional results, and present supplemental charts and tables.
The primary data source for this project is the MXPIs research database, which differs from the production database in structure and content. The MXPIs research database has fewer access restrictions than the production database because it contains only historical data. Additionally, microdata researchers may be interested in knowing how well the research database mimics production estimates. Below, we describe the challenges in replicating production indexes. In the end, we conclude that price indexes calculated with the research database are similar to price indexes published with the production database.
The BLS Handbook of Methods and the MXPIs research database document illustrate the steps for calculating the official import and export price indexes.17 Below, we discuss why we removed items marked as unusable by analysts and created previous-price and monthly price-change variables.
BLS occasionally flags and removes items with large price changes when there are reasons to believe that those changes are due to errors, such as reporting a price in the wrong units. The outlier flag in the research database occasionally misses some items with large price changes that appear to be removed by the time indexes were published. Many of these swings were concentrated before 2012, which leads us to believe there may have been a data-transfer issue. For this reason, we started our index calculation in 2012. We identified potential outliers and removed them if this process caused the relevant four-digit HS index to more closely match the official index. Leaving these prices in the index could result in a large impact from switching formulas for the same reasons mentioned in the “Replication results” section above.
After cleaning the items that may be used for index calculation, we matched these items to item weights from a different research database. The item weight table has a weight_year variable that is updated periodically, but the weights do not become effective until 2 years after the weight_year. For this reason, we specified start months and stop months based on when the next weight becomes effective. After this step, we were able to fill in the in-between months with the weight in the start month.
The last step to this initial process was to map the items to their weight groups. The weight group consists of the classification_group variable and the rts_id variable, which is a respondent identifier, in the research database, which can be linked to the items and year through the map data table. The product of this mapping is a data table called the price_weight_group, which is the first table used to calculate elementary-level indexes.
This process was repeated to obtain weights and mapping information for classification groups and HS, aggregating to two-digit HS. After collecting price, weight, and hierarchy information, we calculated indexes by using the appropriate formulas.
The index calculation at the weight-group level was completed by using equation (1) and equation (2) with the available trade weights and prices, and this calculation allows us to make long-term relatives for each item and create a short-term relative for the weight-group index. This process was then repeated to get classification-group, stratum, and ultimately two-digit indexes.
We assessed this method by using statistical comparisons between the calculated and official indexes to determine if replication was close enough. In addition to the index comparisons shown above, we put the indexes into groups based on statistics chosen to determine how close the indexes replicated. As we have already discussed, we calculated three statistics: a correlation coefficient, a root-mean-square error, and a mean absolute error. All analyses were performed on the short-term relatives for both series. Indexes were considered extremely well replicated if all three of the following criteria were met: a correlation coefficient above 0.85, a root-mean-square error less than 2.0, and a mean absolute error less than 1.0. An index was classified as not well replicated if there was at least one failure, and a failure is defined as follows: a correlation coefficient below 0.2, a root-mean-square error above 5.0, and a mean absolute error above 2.0. All other indexes were classified as well replicated. This analysis was done for both two- and four-digit indexes. Index classification counts per group are shown in table A-1.
| Index | Extremely well replicated | Well replicated | Not well replicated |
|---|---|---|---|
| Imports | 39 | 91 | 7 |
| Exports | 34 | 73 | 7 |
| Source: U.S. Bureau of Labor Statistics. | |||
We picked the aforementioned statistical cutoffs to separate indexes into groups and compared the groups both visually and statistically. For verification purposes, the groups were selected by how well the formula replicated official MXPIs. The statistical comparison of these groups shown in table A-1 was completed by using the average yearly difference method described above. Also, when we combined both visual comparisons, such as those shown in chart 1 and chart 2, with table A-1, then this gave us confidence in the cutoffs of these groups and in being able to evaluate extremely well replicated indexes and well-replicated indexes with the geometric method.
The above process was designed to replicate the MXPIs. We wanted to keep the weights consistent in both the geometric and Laspeyres indexes when changing to a geometric index calculation, which would keep the result of the geometric index to be less than or equal to the Laspeyres index in all cases. The same aggregation process was performed by using equation (4) and equation (6). If the equations had a change in the way weights for items were calculated, the following equation would be used:
![]() .
.
If this equation is used, then the headline results for Laspeyres and geometric comparisons would change to the comparisons shown in table A-2. These results show 50 percent to 60 percent of the impact seen in the consistent-weight method. (See table 1.) The reason for such smaller results is that with this choice of weights the geometric index can be higher than the Laspeyres index in some cases. Thus, the smaller impact that this method shows is due to some indexes having higher inflation with a geometric calculation, which decreases the average difference.
| Index | Weight group only, mean difference | Weight group only, median difference | Classification and weight groups, mean difference | Classification and weight groups, median difference |
|---|---|---|---|---|
| Imports | 0.086 | 0.094 | 0.223 | 0.249 |
| Exports | 0.138 | 0.152 | 0.259 | 0.248 |
| Source: U.S. Bureau of Labor Statistics. | ||||
With the March 2025 data release, the BLS International Price Program will begin using administrative trade data to calculate classification-group indexes for about one-third of trade.18 This replacement may affect our findings for multiple reasons, including that the indexes being replaced are more or less likely to have multiple items in their weight groups. In preparing for this change, we first studied which four-digit HS and two-digit HS codes are most affected by the geometric Young formula. Most of these high impact indexes do not contain the classification groups that will be replaced. Next, we removed the classification groups set to be replaced and calculated new headline Laspeyres and geometric Young indexes. Table A-3 shows the results of this exercise. We find that excluding the indexes that will be replaced only slightly attenuates our results. The difference between a geometric Young index and a Laspeyres index drops by only 0.2 percentage point for imports and 0.07 percentage point for exports when excluding these classification groups.
| Index | CTD classification groups included, index level difference | CTD classification groups included, percent difference | CTD classification groups excluded, index level difference | CTD classification groups excluded, percent difference |
|---|---|---|---|---|
| Imports | –4.19 | –3.81 | –3.85 | –3.61 |
| Exports | –5.23 | –4.56 | –5.22 | –4.49 |
| Note: CTD = Census Trade Data. The units for the level difference are index points. Source: U.S. Bureau of Labor Statistics. | ||||
In this section of the appendix, we provide additional charts that provide more detail on some of our results and numbers.
Chart A-1 and chart A-2 show the percentage-point difference in the 12-month change of headline inflation for imports and exports when the geometric Young method is used through the classification-group level for the period from 2013 to 2022. Over this period, the yearly difference for imports ranged from 0.1 percentage point to 0.8 percentage point. For exports, the yearly difference was relatively stable at around 0.5 percentage point until 2019, when the difference declined. In 2021, exports abruptly increased to 1.2 percentage points. In 2022, exports declined to almost 0 percentage point. Exports had larger swings than imports. These charts demonstrate how formula choice can affect topline inflation differently for exports and imports.
| Month | Difference |
|---|---|
| January 2013 | 0.474 |
| February 2013 | 0.415 |
| March 2013 | 0.432 |
| April 2013 | 0.441 |
| May 2013 | 0.469 |
| June 2013 | 0.467 |
| July 2013 | 0.463 |
| August 2013 | 0.462 |
| September 2013 | 0.471 |
| October 2013 | 0.465 |
| November 2013 | 0.454 |
| December 2013 | 0.446 |
| January 2014 | 0.423 |
| February 2014 | 0.422 |
| March 2014 | 0.397 |
| April 2014 | 0.378 |
| May 2014 | 0.349 |
| June 2014 | 0.357 |
| July 2014 | 0.358 |
| August 2014 | 0.357 |
| September 2014 | 0.341 |
| October 2014 | 0.348 |
| November 2014 | 0.332 |
| December 2014 | 0.343 |
| January 2015 | 0.362 |
| February 2015 | 0.346 |
| March 2015 | 0.343 |
| April 2015 | 0.313 |
| May 2015 | 0.316 |
| June 2015 | 0.300 |
| July 2015 | 0.291 |
| August 2015 | 0.280 |
| September 2015 | 0.273 |
| October 2015 | 0.294 |
| November 2015 | 0.309 |
| December 2015 | 0.302 |
| January 2016 | 0.406 |
| February 2016 | 0.448 |
| March 2016 | 0.466 |
| April 2016 | 0.470 |
| May 2016 | 0.467 |
| June 2016 | 0.483 |
| July 2016 | 0.491 |
| August 2016 | 0.496 |
| September 2016 | 0.507 |
| October 2016 | 0.486 |
| November 2016 | 0.480 |
| December 2016 | 0.478 |
| January 2017 | 0.464 |
| February 2017 | 0.493 |
| March 2017 | 0.518 |
| April 2017 | 0.657 |
| May 2017 | 0.659 |
| June 2017 | 0.651 |
| July 2017 | 0.642 |
| August 2017 | 0.646 |
| September 2017 | 0.640 |
| October 2017 | 0.733 |
| November 2017 | 0.737 |
| December 2017 | 0.728 |
| January 2018 | 0.610 |
| February 2018 | 0.599 |
| March 2018 | 0.559 |
| April 2018 | 0.424 |
| May 2018 | 0.416 |
| June 2018 | 0.412 |
| July 2018 | 0.419 |
| August 2018 | 0.398 |
| September 2018 | 0.401 |
| October 2018 | 0.270 |
| November 2018 | 0.260 |
| December 2018 | 0.248 |
| January 2019 | 0.230 |
| February 2019 | 0.158 |
| March 2019 | 0.149 |
| April 2019 | 0.140 |
| May 2019 | 0.139 |
| June 2019 | 0.144 |
| July 2019 | 0.125 |
| August 2019 | 0.140 |
| September 2019 | 0.137 |
| October 2019 | 0.144 |
| November 2019 | 0.144 |
| December 2019 | 0.157 |
| January 2020 | 0.163 |
| February 2020 | 0.178 |
| March 2020 | 0.187 |
| April 2020 | 0.191 |
| May 2020 | 0.183 |
| June 2020 | 0.165 |
| July 2020 | 0.176 |
| August 2020 | 0.166 |
| September 2020 | 0.162 |
| October 2020 | 0.172 |
| November 2020 | 0.172 |
| December 2020 | 0.177 |
| January 2021 | 0.157 |
| February 2021 | 0.159 |
| March 2021 | 0.157 |
| April 2021 | 0.186 |
| May 2021 | 0.225 |
| June 2021 | 0.254 |
| July 2021 | 0.288 |
| August 2021 | 0.295 |
| September 2021 | 0.301 |
| October 2021 | 0.323 |
| November 2021 | 0.326 |
| December 2021 | 0.327 |
| January 2022 | 0.443 |
| February 2022 | 0.436 |
| March 2022 | 0.412 |
| April 2022 | 0.428 |
| May 2022 | 0.399 |
| June 2022 | 0.385 |
| July 2022 | 0.450 |
| August 2022 | 0.389 |
| September 2022 | 0.375 |
| October 2022 | 0.322 |
| November 2022 | 0.331 |
| December 2022 | 0.312 |
| Note: This chart shows the difference between a Laspeyres formula and a geometric Young formula in the calculation of a 12-month change of headline inflation for imports through the classification-group level. Source: U.S. Bureau of Labor Statistics. | |
| Month | Difference |
|---|---|
| January 2013 | 0.469 |
| February 2013 | 0.478 |
| March 2013 | 0.491 |
| April 2013 | 0.487 |
| May 2013 | 0.479 |
| June 2013 | 0.468 |
| July 2013 | 0.447 |
| August 2013 | 0.463 |
| September 2013 | 0.449 |
| October 2013 | 0.437 |
| November 2013 | 0.409 |
| December 2013 | 0.404 |
| January 2014 | 0.404 |
| February 2014 | 0.392 |
| March 2014 | 0.377 |
| April 2014 | 0.366 |
| May 2014 | 0.369 |
| June 2014 | 0.392 |
| July 2014 | 0.402 |
| August 2014 | 0.379 |
| September 2014 | 0.377 |
| October 2014 | 0.378 |
| November 2014 | 0.380 |
| December 2014 | 0.401 |
| January 2015 | 0.434 |
| February 2015 | 0.428 |
| March 2015 | 0.451 |
| April 2015 | 0.483 |
| May 2015 | 0.483 |
| June 2015 | 0.487 |
| July 2015 | 0.466 |
| August 2015 | 0.461 |
| September 2015 | 0.462 |
| October 2015 | 0.457 |
| November 2015 | 0.449 |
| December 2015 | 0.443 |
| January 2016 | 0.431 |
| February 2016 | 0.438 |
| March 2016 | 0.435 |
| April 2016 | 0.413 |
| May 2016 | 0.443 |
| June 2016 | 0.438 |
| July 2016 | 0.475 |
| August 2016 | 0.498 |
| September 2016 | 0.491 |
| October 2016 | 0.524 |
| November 2016 | 0.537 |
| December 2016 | 0.536 |
| January 2017 | 0.578 |
| February 2017 | 0.578 |
| March 2017 | 0.576 |
| April 2017 | 0.611 |
| May 2017 | 0.584 |
| June 2017 | 0.564 |
| July 2017 | 0.514 |
| August 2017 | 0.491 |
| September 2017 | 0.545 |
| October 2017 | 0.538 |
| November 2017 | 0.560 |
| December 2017 | 0.562 |
| January 2018 | 0.573 |
| February 2018 | 0.583 |
| March 2018 | 0.601 |
| April 2018 | 0.616 |
| May 2018 | 0.650 |
| June 2018 | 0.650 |
| July 2018 | 0.630 |
| August 2018 | 0.614 |
| September 2018 | 0.553 |
| October 2018 | 0.503 |
| November 2018 | 0.476 |
| December 2018 | 0.434 |
| January 2019 | 0.347 |
| February 2019 | 0.344 |
| March 2019 | 0.300 |
| April 2019 | 0.240 |
| May 2019 | 0.199 |
| June 2019 | 0.183 |
| July 2019 | 0.198 |
| August 2019 | 0.206 |
| September 2019 | 0.195 |
| October 2019 | 0.218 |
| November 2019 | 0.220 |
| December 2019 | 0.237 |
| January 2020 | 0.164 |
| February 2020 | 0.124 |
| March 2020 | 0.109 |
| April 2020 | 0.109 |
| May 2020 | 0.127 |
| June 2020 | 0.149 |
| July 2020 | 0.174 |
| August 2020 | 0.230 |
| September 2020 | 0.299 |
| October 2020 | 0.322 |
| November 2020 | 0.324 |
| December 2020 | 0.367 |
| January 2021 | 0.534 |
| February 2021 | 0.698 |
| March 2021 | 0.961 |
| April 2021 | 1.137 |
| May 2021 | 1.182 |
| June 2021 | 1.173 |
| July 2021 | 1.223 |
| August 2021 | 1.094 |
| September 2021 | 1.064 |
| October 2021 | 0.988 |
| November 2021 | 0.929 |
| December 2021 | 0.867 |
| January 2022 | 0.686 |
| February 2022 | 0.465 |
| March 2022 | 0.169 |
| April 2022 | 0.055 |
| May 2022 | 0.076 |
| June 2022 | 0.027 |
| July 2022 | 0.015 |
| August 2022 | 0.000 |
| September 2022 | 0.009 |
| October 2022 | 0.159 |
| November 2022 | 0.150 |
| December 2022 | 0.095 |
| Note: This chart shows the difference between a Laspeyres formula and a geometric Young formula in the calculation of a 12-month change of headline inflation for exports through the classification-group level. Source: U.S. Bureau of Labor Statistics. | |
Chart A-3 and chart A-4 break down the impact of the geometric Young formula for four-digit indexes on import and export indexes when the formula is used through the classification-group level or only up to the weight-group level. These charts show that exports tend to be affected more than imports by a switch to the geometric Young formula at both the classification- and weight-group levels. The charts also show the additive impact of switching to the geometric Young formula at both the weight-group and classification-group levels, as opposed to just the weight-group level (note the differences are larger in chart A-3 than chart A-4).
| Difference (in percentage points) | Imports (in percent) | Exports (in percent) |
|---|---|---|
| 0 | 2.308 | 1.869 |
| ≤ 0.1 | 28.462 | 28.037 |
| 0.2 | 22.308 | 14.953 |
| 0.3 | 16.154 | 13.084 |
| 0.4 | 10.769 | 5.607 |
| 0.5 | 4.615 | 5.607 |
| 0.6 | 5.385 | 3.738 |
| 0.7 | 2.308 | 3.738 |
| 0.8 | 2.308 | 4.673 |
| 0.9 | 0.769 | 3.738 |
| > 0.9 | 4.615 | 14.953 |
| Note: This chart shows the split between imports and exports in the distribution of impact of a geometric Young used through the classification-group level. The difference is a Laspeyres formula calculation minus a geometric Young formula calculation. Source: U.S. Bureau of Labor Statistics. | ||
| Difference (in percentage points) | Imports (in percent) | Exports (in percent) |
|---|---|---|
| 0 | 3.846 | 1.869 |
| ≤ 0.1 | 54.615 | 44.860 |
| 0.2 | 18.462 | 12.150 |
| 0.3 | 9.231 | 11.215 |
| 0.4 | 6.923 | 4.673 |
| 0.5 | 2.308 | 1.869 |
| 0.6 | 0.769 | 5.607 |
| 0.7 | 0.769 | 3.738 |
| 0.8 | 0.769 | 2.804 |
| 0.9 | 0.000 | 2.804 |
| > 0.9 | 2.308 | 8.411 |
| Note: This chart shows the split between imports and exports in the distribution of impact of a geometric Young used only at the weight-group level. The difference is a Laspeyres formula calculation minus a geometric Young formula calculation. Source: U.S. Bureau of Labor Statistics. | ||
Austin Enderson-Ohrt, and Dominic Smith, "The geometric Young formula for elementary aggregate import and export price indexes," Monthly Labor Review, U.S. Bureau of Labor Statistics, February 2025, https://doi.org/10.21916/mlr.2025.3
1 A modified Laspeyres formula is also known as a Lowe formula. For more information, see “International Price Program: calculation,” Handbook of Methods (U.S. Bureau of Labor Statistics, last modified August 1, 2024), https://www.bls.gov/opub/hom/ipp/calculation.htm.
2 Each code represents a number of digits corresponding to a product or a group of products. More digits indicate more specific product categories, while fewer digits indicate broader product categories.
3 “Consumer Price Index: overview,” Handbook of Methods (U.S. Bureau of Labor Statistics, last modified September 6, 2023), https://www.bls.gov/opub/hom/cpi/home.htm.
4 Robert S. Martin, Andy Sadler, Sara Stanley, William Thompson, and Jonathan Weinhagen, “The geometric Young formula for elementary aggregate producer price indexes,” Journal of Official Statistics, vol. 38, no. 1, March 2022, pp. 239–253, https://doi.org/doi:10.2478/jos-2022-0011; and Sara Stanley, "Introducing Producer Price Index research series based on a geometric-mean formula," Monthly Labor Review, May 2024, https://doi.org/10.21916/mlr.2024.8.
5 Martin et al. “The geometric Young formula for elementary aggregate producer price indexes.”
6 The Consumer Price Index (CPI) program does not use a geometric mean for all elementary aggregates. Stanley, in “Introducing Producer Price Index research series based on a geometric-mean formula,” discusses this point as follows: “In 1999, BLS introduced a geomean formula for calculating most elementary-level CPI estimates. This shift largely aimed to capture consumer substitutions toward less expensive products when product prices change at varying rates. Because substitution considerations provide the primary rationale for using geometric means in the CPI, not all elementary-level CPIs are calculated with a geomean formula. Indexes for which substitution is less common, such as those for certain utilities, government fees, or medical care services, are still calculated with a modified Laspeyres formula.” For additional information, see Kenneth V. Dalton, John S. Greenlees, and Kenneth J. Stewart, “Incorporating a geometric mean formula into the CPI,” Monthly Labor Review, October 1998, https://www.bls.gov/opub/mlr/1998/10/art1full.pdf.
7 Readers who are interested in the U.S. Import and Export Price Indexes (MXPIs) production database produced by the U.S. Bureau of Labor Statistics (BLS) should see the following webpage to apply for access to the database: “BLS restricted data access” (U.S. Bureau of Labor Statistics), https://www.bls.gov/rda/.
8 Schedule B numbers are 10-digit classification codes that differentiate between the products being traded. They are maintained by the U.S. Census Bureau.
9 “International Price Program: overview,” Handbook of Methods (U.S. Bureau of Labor Statistics, last modified August 1, 2024), https://www.bls.gov/opub/hom/ipp/home.htm.
10 The sample weights are updated when each item is initiated into MXPIs. The trade-dollar weights used in the MXPIs are lagged from 12 to 24 months and are updated in January of each year, which implies b < t.
11 We use a database provided by the MXPIs program. The database includes published and unpublished index series.
12 Martin et al., “The geometric Young formula for elementary aggregate producer price indexes.”
13 Ibid.
14 We show the distribution of changes separately for imports and exports in chart A-3 and chart A-4.
15 Administrative trade data are customs data covering the universe of trade transactions. For more information about administrative trade data, see Dominic Smith, Austin Enderson-Ohrt, Matthew Fisher, Christopher Grant, Angel Wong, and Benjamin Wullbrandt, “Enhancing import and export price indexes: a new methodology using administrative trade data,” Working Paper 578 (U.S. Bureau of Labor Statistics, December 10, 2024), https://www.bls.gov/osmr/research-papers/2024/ec240080.htm.
16 Martin et al., “The geometric Young formula for elementary aggregate producer price indexes.”
17 “International Price Program: overview;” and Mina Kim, Taylor Blackburn, and Rozi Ulics, “IPP Research Database V1.0” (U.S. Bureau of Labor Statistics, September 30, 2015). The article by Kim, Blackburn, and Ulics is a BLS internal document. Researchers with approved access to the confidential MXPIs microdata who are interested in obtaining a copy of the Kim, Blackburn, and Ulics article should contact the BLS Division of International Prices (https://www.bls.gov/mxp/contact.htm).
18 Don Fast, Susan E. Fleck, and Dominic A. Smith, “Unit value indexes for exports––new developments using administrative trade data,” Journal of Official Statistics, vol. 38, no. 1, March 2022, pp. 83–106, https://doi.org/10.2478/jos-2022-0005.