An official website of the United States government
 United States Department of Labor
United States Department of Labor
The following section explains how the Current Employment Statistics-National (CES-N) program produces employment, hours, and earnings. The CES-State and Area (CES-SA) program uses the same sample and collection methods, thus references to CES apply to both CES-N and CES-SA programs.
The CES-N program uses a matched sample concept and weighted sample data to produce employment, hours, and earnings estimates. The methods are summarized in exhibit 1 and described in more detail below.
| Employment, hours, and earnings | Basic estimating cell (industry, 6-digit published level) | Aggregate industry level (super sector and, where stratified, industry) | Annual average data |
|---|---|---|---|
|
All employees |
All employee estimate for previous month multiplied by weighted ratio of all employees in current month to all employees in previous month, for sample establishments that reported for both months, plus net birth-death forecast. | Sum of all employee estimates for component cells. | Sum of monthly estimates divided by 12. |
|
Average weekly hours of all employees |
All employee hours divided by number of all employees. | Average, weighted by all employees, of the average weekly hours for component cells. | Annual total of aggregate hours (all employees multiplied by average weekly hours) divided by annual sum of all employees. |
|
Average weekly overtime hours of all employees |
All employee overtime hours divided by number of all employees. | Average, weighted by all employees, of the average weekly overtime hours for component cells. | Annual total of aggregate overtime hours (all employees multiplied by average weekly overtime hours) divided by annual sum of all employees. |
|
Average hourly earnings of all employees |
All employee payroll divided by all employee hours. | Average, weighted by aggregate hours, of the average hourly earnings for component cells. | Annual total of aggregate payrolls (all employees multiplied by weekly hours and hourly earnings) divided by annual aggregate hours. |
|
Average weekly earnings of all employees |
Product of all employee average weekly hours and all employee average hourly earnings. | Product of all employee average weekly hours and all employee average hourly earnings. | Sum of monthly all employee aggregate payrolls divided by the sum of monthly all employees. |
|
Production and nonsupervisory employees |
All employee estimate for current month multiplied by weighted ratio of production and nonsupervisory employees to all employees in sample establishments for current month. | Sum of estimates of production and nonsupervisory employees for component cells. | Sum of monthly estimates divided by 12. |
|
Women employees |
All employee estimate for current month multiplied by weighted ratio of women employees to all employees in sample establishments for current month. | Sum of estimates of women employees for component cells. | Sum of monthly estimates divided by 12. |
|
Average weekly hours of production and nonsupervisory employees |
Production and nonsupervisory employee hours divided by number of production or nonsupervisory employees. | Average, weighted by production and nonsupervisory employment, of the average weekly hours for component cells. | Annual total of aggregate hours (production and nonsupervisory employment multiplied by average weekly hours) divided by annual sum of production and nonsupervisory employment. |
|
Average weekly overtime hours of production and nonsupervisory employees (manufacturing industries only) |
Production employee overtime hours divided by number of production employees. | Average, weighted by production employment, of the average weekly overtime hours for component cells. | Annual total of aggregate overtime hours (production and nonsupervisory employment multiplied by average weekly overtime hours) divided by annual sum of production and nonsupervisory employment. |
|
Average hourly earnings of production and nonsupervisory employees |
Total production and nonsupervisory employee payroll divided by total production and nonsupervisory employee hours. | Average, weighted by aggregate hours, of the average hourly earnings for component cells. | Annual total of aggregate payrolls (production and nonsupervisory employment multiplied by weekly hours and hourly earnings) divided by annual aggregate hours. |
|
Average weekly earnings of production and nonsupervisory employees |
Product of production and nonsupervisory employee average weekly hours and production and nonsupervisory employee average hourly earnings. | Product of production and nonsupervisory employee average weekly hours and production and nonsupervisory employee average hourly earnings. | Sum of monthly aggregate payrolls divided by the sum of monthly production employees. |
The CES-N sample is stratified into basic estimation cells for the purpose of computing all employee (AE) estimates. Estimating cell structures may differ for production and nonsupervisory employees (PE), women employees (WE), and hours and earnings for both AE and PE. Cells are defined primarily by industry. Geographic stratification is also used for some construction and government industries. Estimation cells may be defined at the 3-, 4-, 5-, or 6-digit North American Industry Classification System (NAICS) level. This level varies by industry to ensure that basic estimating cells contain adequate sample to produce reliable estimates. For numbers of estimation cells in the current year’s data, see the Industry classification section of the CES Overview webpage.
All basic estimates are used to aggregate to higher summary cell levels up to total nonfarm for both AE and WE and up to total private for all other datatypes.
In addition to the basic estimation cells, CES-N estimates a small number of series independently; these series are not used for aggregating to summary cell levels.
A matched sample is defined as all sample units that have reported data for the reference month and the month prior. Exhibit 2 shows all data that must be reported and matched for estimating each series type. Regardless of the data type being estimated, the respondent must provide AE for both months. The matched sample excludes any sample unit reporting that it is out of business and has zero employees. The section on birth–death model estimation more fully describes this aspect of the estimation methodology.
| Estimate | Reported data types |
|---|---|
|
All employees |
All employees |
|
Women employees |
All employees, women employees |
|
Production and nonsupervisory employees |
All employees, production and nonsupervisory employees |
|
Average weekly hours of all employees |
All employees, total weekly hours of all employees |
|
Average hourly earnings of all employees |
All employees, total weekly hours of all employees, total weekly payroll of all employees |
|
Average weekly overtime of all employees |
All employees, total weekly overtime hours of all employees |
|
Average weekly hours of production and nonsupervisory employees |
Production and nonsupervisory employees, total weekly hours of production and nonsupervisory employees |
|
Average hourly earnings of production and nonsupervisory employees |
Production and nonsupervisory employees, total weekly hours of production and nonsupervisory employees, total weekly payroll of production and nonsupervisory employees |
|
Average weekly overtime of production and nonsupervisory employees |
Production and nonsupervisory employees, total weekly overtime hours of production and nonsupervisory employees |
CES-N uses the weighted-link-relative formula, shown in equation 1, to estimate AE series in basic estimating cells. The formula applies the relative change in the weighted matched sample of the estimating cell to move the previous month’s estimate forward to the current reference month. A model-based component is added to account for the net employment change resulting from business births and deaths not captured by the sample.
In some cases, a respondent’s microdata may be identified as an outlier and may be treated as atypical. The atypical microdata is removed from the prior month’s estimate and from the matched sample, the estimate is calculated, and then the atypical microdata is added back for the current month. Atypical treatment allows CES-N to use valid microdata to only represent the change in that establishment, but not for changes in other establishments. A strike or damage to an individual establishment that leads to abnormal employment change, for example, would be identified as atypical.
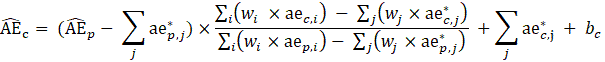
where
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For all data types other than AE, CES-N uses matched sample and the weighted-difference-link-and-taper estimator. The difference link accounts for the over-the-month change in the sampled units, while the tapering feature keeps the estimates close to the overall sample average over time by using a composite base derived from the prior month’s estimate and matched sample average. The taper is considered a level correction because no benchmark source exists for non-AE data types. This estimator promotes continuity by heavily favoring the estimate for the previous month’s estimate (usually by 90 percent). Reported microdata may be identified as atypical, whereby the atypical microdata is subtracted from the base and matched samples, then added back after calculating the current estimate to represent the individual establishment only.
Variables used in equations 2 to 4 are defined below equation 2.
CES-N estimates a ratio of PE to AE (PER) using the weighted-difference-link-and-taper formula. The resulting ratio is then multiplied by the current month’s AE estimate to obtain a current estimate of PE.
![]()
where
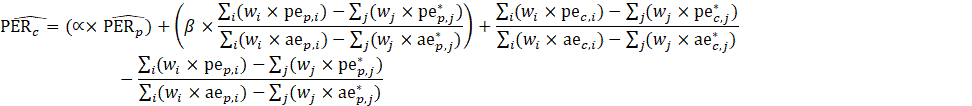
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For all variables used in the equations above:
The estimator for WE takes the same form as the estimator for PE, where PE and PER represent the estimates for WE and WE-to-AE ratio (WER), respectively, and pe represents women employees in the matched sample.
The CES-N hours and earnings series are derived from reports of payrolls and the corresponding paid hours for all employees and for various types of production employees. Hours and earnings are for private-sector employees.
The estimator for average weekly hours (AWH), shown in equation 3, uses a composite base of the prior month’s AWH estimate and sample ratio of total hours paid-to-AE (AWH), then the change in the sample average ratios (current minus previous) is added to set the over-the-month change.
The estimator for average weekly hours for production and nonsupervisory employees takes the same form as average weekly hours for all employees, where AE and AWH represent estimates of PE and AWH for PE, respectively, and ae and wh represent production employees and weekly hours for production and nonsupervisory employees in the matched sample, respectively.
The estimator for average hourly earnings (AHE), shown in equation 4, uses a composite base of the prior month’s AHE estimate and sample ratio of total weekly payroll-to-total weekly hours (ahe), then the change in the sample average ratios is added to set the over-the-month change.
The estimator for average hourly earnings for production and nonsupervisory employees (PE-AHE) takes the same form as average hourly earnings for all employees (AE-AHE), where AE, AWH, and AHE represent estimates of PE and their hours and earnings, and the matched sample pr and wh variables represent the matched sample variables of total payroll and total hours for PE.
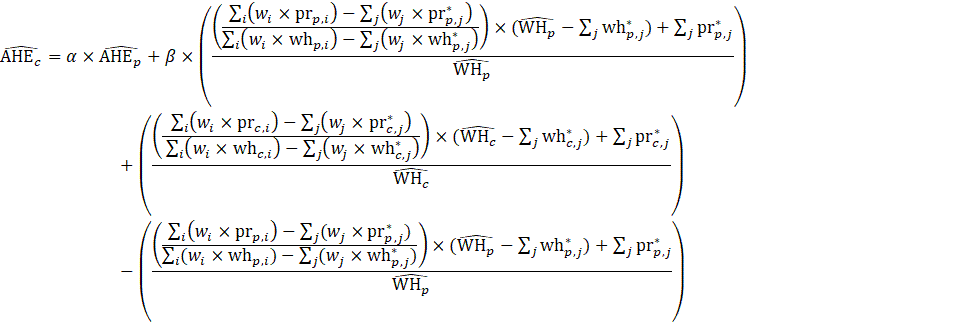
Average weekly overtime hours (AWOH) estimates use a composite base of the prior month’s AWOH estimate and sample ratio of total-weekly-overtime-hours-to-AE, then the change in the sample average ratios is added to set the over-the-month change. Overtime estimates are calculated for manufacturing industries only.
The estimators for AWOH take the same form as AWH, where AWH represents the estimates of AWOH and wh represents the matched sample for total overtime hours.
Similar substitutions also can be made to obtain estimates of AWOH of PE, where AE and AWH represent estimates of PE and AWOH of production and nonsupervisory employees, respectively, and the matched sample totals ae and wh represent matched sample totals for PE and total overtime hours for production and nonsupervisory employees, respectively.
CES-N produces all employee estimates for residential and nonresidential specialty trade contractors (NAICS 238). Independent estimates for these series are made monthly and raked proportionally to the estimates produced using the NAICS-based CES industry structure to ensure that the sum of residential specialty trade contractors and nonresidential specialty trade contractors series sums to the published total for specialty trade contractors.
Estimates are derived independently for the residential and nonresidential groups at the 4-digit NAICS level for each region. The regional estimates are rounded and summed to the 4-digit NAICS level for both the residential and nonresidential groups. Within each 4-digit NAICS series, ratios of residential-to-total employment and nonresidential-to-total employment are calculated.
At the 4-digit NAICS level, the sum of the residential and nonresidential series is subtracted from the official industry-region cell structure total to determine the amount that must be raked. This total amount is multiplied by the ratios to determine what percentages of the raked amount should be applied to the residential group and to the nonresidential group.
Once the residential and nonresidential groups receive their proportional amount of raked employment, the two groups are aggregated again to the 4-digit NAICS level. At this point they are equal to the 4-digit NAICS totals of the CES industry-region cell structure. This raking process forces additivity at the 3-digit NAICS level.
Only estimates of AE are made for the residential and nonresidential specialty trade contractor series.
Non-response from certainty units that historically exhibit consistent, seasonal differences from the rest of the population is accounted for through imputation. If one of these establishments fails to report CES data for the current month, the establishment’s historical over-the-month change data is used in the imputation to capture the specific seasonal movement of the establishment.
Relatively small sample size in some industries limits the reliability of the weighted-link-relative estimator for all employees (AE) estimates. The CES-N program produces employment estimates for a few industries, shown in exhibit 3, using the small domain model (SDM), a weighted-least-squares model with two employment inputs:
| Current Employment Statistics industry code | CES industry title |
|---|---|
|
55-533000 |
Lessors of nonfinancial intangible assets (except copyrights works) |
|
60-541213 |
Tax preparation services |
These two over-the-month change estimates are then weighted based on the variance of each of the estimates. The larger the variance of one input estimate relative to the variance of the other input, the smaller the weight applied to that input.
The resulting estimate of current month employment ![]() is defined in equation 5.
is defined in equation 5.
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For national cells, the weight is restricted to a minimum of 0.2 and a maximum of 0.8; however, the weight of the sample estimate in tax preparation services (CES industry 60-541213) is set to zero, since only the forecasts for this industry are used.
Sampling errors are not applicable to the estimates made using SDM. The measure available to judge the reliability of these modeled estimates is their performance over past time periods compared with the universe values for those time periods. These measures are useful; however, it is not certain that the past performance of the modeled estimates accurately reflects their current performance.
The CES sample alone is not sufficient for estimating the total employment level because each month new firms open for business, generating employment that cannot be captured by the sample. There is an unavoidable lag between a firm opening for business and its appearance on the CES sample frame, which is built from unemployment insurance (UI) quarterly tax records. Although, UI tax records cover nearly all U.S. employers and include business births, they only become available for updating to the CES sampling frame 7 to 9 months after the reference month. After establishment births appear on the frame, additional time is required for sampling, enrolling, and collecting payroll data. In practice, CES cannot sample and begin to collect data from new firms until they are at least a year old.
There is a somewhat different issue in capturing employment loss from business deaths through monthly sample collection. Businesses that have closed are unlikely to respond to the survey, and data collectors may not be able to ascertain until after the monthly collection period that firms have in fact gone out of business. As with business births, confirmation of business deaths eventually becomes available from the lagged UI tax records.
Difficulty in capturing information from business birth and death units is not unique to the CES program; virtually all current business surveys face these limitations. CES adjusts for these limitations explicitly, using a statistical modeling technique in conjunction with the sample for estimating employment for private-sector industries. Without the net birth–death model-based adjustment, the CES nonfarm payroll employment estimates would be considerably less accurate.
The CES-N program separates the net birth–death methodology into two steps. The process applies only to nonfarm industries in the private sector.
The first step is to exclude from the sample employment losses from business deaths to offset a portion of employment gains from business births. Research and data have shown that employment increases from firm births roughly offset employment decreases from firm deaths in most months; therefore, step one accounts for most of the net employment change from business births and deaths.
To accomplish step one, CES-N excludes reports with zero employment from the sample. Nonresponding sample units are automatically excluded from the matched sample, because they have no data for the reference month. These exclusions from the matched sample result in an over-the-month change that is based solely on employment from continuing businesses and effectively keep employment from business deaths in the estimates to represent employment from business births that occur after the sample was selected.
Step one accounts for most of the birth–death employment, but not all of it.
The second step is to model the net birth–death employment residual not accounted for in step one. The CES-N program adjusts its sample-based estimates for the net birth–death employment missed by step one using autoregressive integrated moving average (ARIMA) modeling, an econometric technique often used to analyze and forecast time series. From the Quarterly Census of Employment and Wages (QCEW) universe employment series, each establishment is classified as a continuing, birth, or death unit. The process outlined in step one is applied to the QCEW data. Over-the-month changes are calculated from the continuing units, and deaths are used to impute for births. The differences between simulated estimates and actual employment totals measured by the QCEW each month are input into the ARIMA model to derive the net birth–death employment forecast.
The inputs to the ARIMA model depend on the age of the selected sample, which is selected in 1 year and rotated into production by industry sector and quarter over the following year. Quarterly sample rotation results in differently aged samples by industry sector and has an inherent effect on death values. To control for sample age, net birth–death forecasts are based on input data either 1 year out or 2 years out from selection. Exhibit 4 shows which sample is used to produce estimates for the first quarter of year t through the fourth quarter of year t. In the first quarter of year t, estimates for all industries are based on the sample selected in year t-1, and all net birth–death forecasts are based on births and deaths in the first year after selection. In the second quarter of year t, sample selected in year t-1 is used for mining and logging; for trade, transportation, and utilities; and for financial activities; the net birth–death forecasts for these industries are based on input data 1 year after the sample was selected. All other industries are based on the prior sample year t-2 and require a forecast based on net birth–deaths in the second year after selection. In the third quarter of year t, two additional industries—construction and leisure and hospitality—are rotated to the year t-1 sample and require a forecast from inputs that are 1 year out, and the remaining industries on year t-2 samples require a forecast from inputs that are 2 years out. This process repeats with more industries rotating in on the newer sample and requiring the 1-year-out forecast until the first quarter of year t+1 when all private-sector industries are based on year t-1 sample.
| Industry | Major industry | Second quarter, Yt | Third quarter, Yt | Fourth quarter, Yt | First quarter, Yt+1 |
|---|---|---|---|---|---|
|
Mining and logging |
10 | Year t-1 sample | Year t-1 sample | Year t-1 sample | Year t-1 sample |
|
Trade, transportation, and utilities |
40 | ||||
|
Financial activities |
55 | ||||
|
Construction |
20 | Year t-2 sample | |||
|
Leisure and hospitality |
70 | ||||
|
Information |
50 | Year t-2 sample | |||
|
Professional and business services |
60 | ||||
|
Other services |
80 | ||||
|
Manufacturing |
30 | Year t-2 sample | |||
|
Private education and health services |
65 | ||||
Quarterly updates to the net birth–death model allow for the incorporation of additional QCEW data as it becomes available. In addition, during annual benchmarking, net birth–death forecasts are revised for April to December based on revised Q1 data. This additional update should minimize the post-benchmark revision of CES estimates at the total private level. (See exhibit 5.) Net birth-death forecasts since the latest benchmark update are available on the CES Net Birth–Death Model website.
| Quarter estimated | QCEW inputs |
|---|---|
|
First |
5 years |
|
Second |
5 years plus 1 quarter |
|
Third |
5 years plus 2 quarters |
|
Fourth |
5 years plus 3 quarters |
For each basic estimating cell, the most recent 6 years of employment data from the longitudinal database (LDB) are partitioned into five 25-month frames plus one half-frame. (See exhibit 6.) The additional half-frame, consisting of 13 months, is necessary to derive 12 months of over-the-month changes for the most recent year t-1 sample.
| Frame | First month of span | Last month of span |
|---|---|---|
|
Frame 1 (half-frame) |
March year t-1 | March year t |
|
Frame 2 |
March year t-2 | March year t |
|
Frame 3 |
March year t-3 | March year t-1 |
|
Frame 4 |
March year t-4 | March year t-2 |
|
Frame 5 |
March year t-5 | March year t-3 |
|
Frame 6 |
March year t-6 | March year t-4 |
The birth–death residuals are calculated working with the frames and treating each microdata unit in the same way that the CES-N treats microdata. Starting with the QCEW microdata for March t-6, microdata is separated into groups of continuous units, death units, and birth units for each reference month from April t-6 through March t-5 as follows:
![]()
The residual birth–death values within the first and second halves of each frame are chained together to form separate time series (one comprised solely of the first half of each year of data, the other of the second half of each year of data).
Continuous samples deteriorate over time as firm deaths are not replenished by births. So, while the older samples continue to be used for some industries, the net birth–death inputs must be aged with the inputs identified in the second year after selection using the same process as the forecast for the 1-year-old sample but aged 1 year.
Over-the-month changes of all net birth–death values are input into the forecasting model for the 1-year-old sample and the 2-year-old sample separately. The resulting forecasts are selected for use in estimation based on the age of the sample used for a given industry and quarter.
Net birth–death forecasts are added to the sample-based components of the estimator for AE to obtain each month’s employment estimate on a not seasonally adjusted basis. Net birth–death forecasts generally show similar seasonal patterns as the sample-based component of the estimates, as some businesses open and close with seasons.
Because of the seasonality of business births and deaths, users who wish to compare the net birth–death model's contribution to overall employment change for a given month should compare it to the not seasonally adjusted employment change for that month. Comparisons to the seasonally adjusted employment changes generally result in an overstatement of the model-based contribution of births and deaths.
CES-N estimates are separated into three types of estimating cells: basic, summary, and independent.
Aggregation starts at the most detailed level, usually the 6-digit NAICS. All 6-digit industries that begin with the same 5 digits are aggregated to that 5-digit NAICS. All 5-digit industries that begin with the same 4 digits are then aggregated to that 4-digit industry. This process continues with all detailed industries falling into 1 of 17 expanded major industry sectors (see exhibit 7), which are further aggregated into 10 supersectors, then goods-producing, private service-providing industries, and finally, to total private and total nonfarm. (See exhibit 8.) Total nonfarm represents the highest summary estimate for all employee (AE) and women employee (WE), while total private represents the highest summary estimate for all other data types.
| Current Employment Statistics industry code | Major sector name | NAICS codes included and ownership |
|---|---|---|
|
10-000000 |
Mining and logging | 1133, 21 / Private |
|
20-000000 |
Construction | 23 / Private |
|
31-000000 |
Durable goods manufacturing | 33, 321 / Private |
|
32-000000 |
Nondurable goods manufacturing | 31, 321 / Private |
|
41-420000 |
Wholesale trade | 42 / Private |
|
42-000000 |
Retail trade | 44-45 / Private |
|
43-000000 |
Transportation and warehousing | 48-49 / Private |
|
44-220000 |
Utilities | 22 / Private |
|
50-000000 |
Information | 51 / Private |
|
55-000000 |
Financial activities | 52,53 / Private |
|
60-000000 |
Professional and business services | 54,55,56 / Private |
|
65-000000 |
Private education and health services | 61,62 / Private |
|
70-000000 |
Leisure and hospitality | 71,72 / Private |
|
80-000000 |
Other services | 811,812,813 / Private |
|
90-910000 |
Federal government | All in-scope NAICS / Federal government |
|
90-920000 |
State government | All in-scope NAICS / State government |
|
90-930000 |
Local government | All in-scope NAICS / Local government |
|
1 CES allocates 3-digit NAICS industries to this major industry sector based on industry description. |
||
| Current Employment Statistics industry code | Aggregate sector name | Sectors included |
|---|---|---|
|
00-000000 |
Total nonfarm | 05-000000 Total private, 90-000000 Government |
|
05-000000 |
Total private | 06-000000 Goods-producing, 08-000000 Private service-providing |
|
06-000000 |
Goods-producing | 10-000000 Mining and logging, 20-000000 Construction, 30-000000 Manufacturing |
|
07-000000 |
Service-providing | 40-000000 Trade, transportation, and utilities, 50-000000 Information, 55-000000 Financial activities, 60-000000 Professional and business services, 65-000000 Private education and health services, 70-000000 Leisure and hospitality, 80-000000 Other services, 90-000000 Government |
|
08-000000 |
Private service-providing | 40-000000 Trade, transportation, and utilities, 50-000000 Information, 55-000000 Financial activities, 60-000000 Professional and business services, 65-000000 Private education and health services, 70-000000 Leisure and hospitality, 80-000000 Other services |
|
30-000000 |
Manufacturing | 31-000000 Durable goods, 32-000000 Nondurable goods |
|
40-000000 |
Trade, transportation, and utilities | 41-420000 Wholesale trade, 42-000000 Retail trade, 43-000000 Transportation and warehousing, 44-220000 Utilities |
|
90-000000 |
Government | 90-910000 Federal government, 90-920000 State government, 90-930000 Local government |
The CES-N industry structure includes several series—total private, motor vehicles and parts manufacturing, health care, and government—that represent summations of industries not found in NAICS. These series are summary cells and are incorporated into the CES-N aggregation structure.
Additional AE series for residential and nonresidential specialty trade contractors are produced as basic series and sum to employment for specialty trade contractors. Specialty trade contractors are also estimated by detailed industry for all data types; these series also aggregate to summary estimates for specialty trade contractors.
Average weekly hours are published in hours rounded to the tenths place. Average hourly earnings and average weekly earnings are published in dollars rounded to the cent.
All employee (AE), production and nonsupervisory employee (PE), and women employee (WE) data types use the same method for aggregation. Basic level estimates rounded to the hundreds are summed to the next higher summary-level estimate and then rounded according to the published precision. The process repeats at each level up to total nonfarm for AE and WE and up to total private for PE.
Aggregate or summary levels of average weekly hours (AWH) are weighted by employment in component industries. Estimates of AWH at the basic levels are multiplied by employment estimates to calculate aggregate hours. Aggregate hours are summed for the basic industries and then divided by their summed employment. The process repeats at each level up to total private. The aggregation method for AWH of AE and PE is identical with the appropriate substitution of AE or PE employment and hours data in equation 7.
![]()
where
![]()
![]()
![]()
Estimates of average hourly earnings (AHE) at the basic level are multiplied by estimates of employment and by average weekly hours to calculate aggregate payroll, which is then summed to the next higher summary industry. The summed payroll data are then divided by the sum of aggregate hours (employment times average weekly hours) of all industries in the summary industry. The aggregation method of AHE for AE and PE is identical with the appropriate substitutions of AE or PE employment, hours, and earnings values in equation 8.
![]()
where
![]()
![]()
![]()
![]()
For the CES-N program, annual benchmarks are constructed to realign the sample-based employment estimates for March of each year with the universe employment counts for that month. Population counts are much less timely than sample-based estimates, and they are used to provide an annual point-in-time census of employment. Only the not seasonally adjusted March estimates are replaced with population counts.
Population counts are derived primarily from administrative files of employees covered by unemployment insurance (UI). All employers covered by UI laws are required to report employment and wage information to their state’s labor market information agency (LMI) four times a year. Approximately 97 percent of employment falling within the scope of the establishment survey is covered by UI. A benchmark for the remaining 3 percent is constructed from alternate sources, primarily records from the Railroad Retirement Board (RRB) and County Business Patterns (CBP). This 3 percent is collectively referred to as noncovered employment. The full benchmark employment level developed for March of a given year replaces that March’s sample-based estimate for each basic cell. Each annual benchmark revision affects 21 months of not seasonally adjusted data from April of the prior year through the following year’s December. The CES-N program also updates seasonal adjustment models with each year’s benchmark revision, and 5 years of seasonally adjusted data are revised with the benchmark release.
Monthly estimates for the year preceding the March benchmark are readjusted using a "wedge-back" procedure. The difference between the final benchmark level and the previously published March sample-based estimate is calculated and spread back across the previous 11 months. The wedge is linear; eleven-twelfths of the March difference is added to the February estimate, ten-twelfths to the January estimate, and so on, back to the previous April estimate, which receives one-twelfth of the March difference. This procedure assumes that the total estimation error since the prior benchmark accumulated at a steady rate.
Estimates for the 7 months following the March benchmark (April through October) are also recalculated. Beginning with the March benchmark as base employment, the post-benchmark estimates are calculated by multiplying the sample-based link, or relative over the month change, for each month to the prior month’s employment estimate and then adding an updated net birth–death forecast.
Following the benchmark revision of basic employment, all estimates are reaggregated, including women employees (WE), production and nonsupervisory employee (PE), hours, and earnings. Existing sample-based ratios for WE and PE are reapplied to the revised employment at the basic level. For basic estimates, average weekly hours (AWH) and average hourly earnings (AHE) do not change. At the summary levels up to total nonfarm, the ratios, hours, and earnings are revised because of changes in employment weights.
Derivative series are recalculated using the revised estimates.
Finally, seasonal adjustment factors for the most recent 5 years are recalculated and applied to all data series.
All data revised as a result of benchmarking are published in February of each year with the first release of January estimates. Additional history may be revised if corrections or series reconstructions are necessary.
Estimates for November and December following the March benchmark are revised due to impacts of both benchmarking and additional sample receipts.
After removing the effect of changes in employment scope, the difference between the universe count of employment for March and its corresponding sample-based estimate represents the benchmark revision. Benchmark revisions from 1979 forward are available in the CES total nonfarm benchmark revisions table.
See the CES Benchmark Article for more details about the most recent benchmark.
Noncovered employment results from a difference in scope between the Current Employment Statistics-National (CES-N) program and the Quarterly Census of Employment and Wages (QCEW) program, whose employment counts are derived from unemployment insurance (UI) tax records filed by individual firms. While most firms are required to pay UI tax for their employees, some types of employees are exempt from their states’ UI tax laws but are still within scope for the CES survey. Examples of the types of employees that may be exempt are students paid by their school as part of a work study program, interns of hospitals paid by the hospital for which they work, employees paid by state and local government and elected officials, independent or contract insurance agents, employees of nonprofit and religious organizations (the largest group of employees not covered), and railroad employees covered under a different system of UI administered by the Railroad Retirement Board (RRB). This employment must be accounted for to set the benchmark level for CES employment.
No single source of noncovered data exists. Therefore, CES-N uses several sources to generate the employment counts, including County Business Patterns (CBP) and the Annual Survey of Public Employment and Payroll (ASPEP), both from the U.S. Census Bureau; the Railroad Retirement Board (RRB); and labor market information agencies (LMIs) within each state.
CES-N calculates most noncovered employment using data from CBP. CBP draws from Social Security filings and other records that include those employees not covered by UI tax laws. Publication of CBP data is lagged by approximately 2 years. (For example, CBP data for 2019 was published in 2021.) To adjust for this lag, CES assumes that the noncovered portion of employment grows or declines at the same rate as the covered portion in its respective industry and moves the CPB data forward using the QCEW trend. The current QCEW employment level is subtracted from the trended CBP figure, and the residual is the noncovered employment level.
Exhibit 9 shows industries that incorporate noncovered employment derived from the CBP as a portion of their total benchmark employment. Except for religious organizations, noncovered employment based on CBP data is calculated using equation 9.
| NAICS code | NAICS industry title |
|---|---|
|
524113 |
Direct life insurance carriers |
|
524114 |
Direct health and medical insurance carriers |
|
524126 |
Direct property and casualty insurance carriers |
|
524127 |
Direct title insurance carriers |
|
524128 |
Other direct insurance carriers, except life, health, & medical |
|
524130 |
Reinsurance carriers |
|
524210 |
Insurance agencies and brokerages |
|
531210 |
Offices of real estate agents and brokers |
|
611110 |
Elementary and secondary schools |
|
611210 |
Junior colleges |
|
611310 |
Colleges and universities |
|
611410 |
Business and secretarial schools |
|
611420 |
Computer training |
|
611430 |
Management training |
|
611511 |
Cosmetology and barber schools |
|
611512 |
Flight training |
|
611513 |
Apprenticeship training |
|
611519 |
Other technical and trade schools |
|
611610 |
Fine arts schools |
|
622110 |
General medical and surgical hospitals1 |
|
622210 |
Psychiatric and substance abuse hospitals1 |
|
622310 |
Other hospitals1 |
|
624310 |
Vocational rehabilitation services |
|
624410 |
Child day care services |
|
813110 |
Religious organizations |
|
813211 |
Grantmaking foundations |
|
813312 |
Environment and conservation organizations |
|
813410 |
Civic and social organizations |
|
813910 |
Business associations |
|
813940 |
Political organizations |
|
813990 |
Other similar organizations |
|
1 Indicates that noncovered employment is calculated for firms owned both privately and by state and local government. |
|
![]()
where
![]()
![]()
![]()
![]()
Noncovered employment for religious organizations is calculated using equation 10. Employment for religious organizations is not published on its own; instead, it is included in religious, grantmaking, civic, professional, and similar organizations (80-813000).
![]()
where
![]()
![]()
![]()
![]()
Public employment for higher education industries listed in exhibit 10 is calculated from ASPEP data using equation 11.
| NAICS code1 | NAICS industry title |
|---|---|
|
611210 |
Junior colleges |
|
611310 |
Colleges and universities |
|
1 Noncovered employment is calculated only for businesses owned by state and local government. |
|
![]()
where
![]()
![]()
![]()
*Public employment data for higher education is the sum of institutional full- and part-time employment and non-institutional full- and part-time employment.
Railroad employment estimates are developed based on data provided by the RRB, which breaks out data by railroad class rather than industry. CES-N prorates data by class to NAICS codes. (See exhibit 11.) RRB data are lagged by 1 year. CES-N carries RRB employment forward using a ratio of the over-the-year percent change in CES-N estimates of rail transportation (NAICS 482) for March of both the benchmark year and the previous year. After applying the ratio, the RRB employment data are mapped and added to the corresponding NAICS-based employment series.
| Rail class | Rail class description | NAICS code | NAICS industry title |
|---|---|---|---|
|
A |
Class 1 line-haul railroads | 482111 | Line-haul railroads |
|
B |
Non-Class 1 line-haul railroads and switching & terminal companies | 488210 | Support activities for rail transportation |
| 482112 | Short line railroads | ||
|
C |
Commuter railroads (includes Amtrak) | 482111 | Line-haul railroads |
| 485111 | Mixed mode transit systems | ||
|
D |
Car-loan railroads | 532411 | Commercial air, rail, and water transportation equipment rental and leasing |
|
E |
Labor organizations | 813930 | Labor unions and similar labor organizations |
|
F |
Miscellaneous employers | 488210 | Support activities for rail transportation |
Over time, some sources from which CES-N draws input data for benchmarking purposes have become unreliable. Where possible, CES-N has tried to find new sources of input data. For series with no reliable input data, listed in exhibit 12, noncovered employment levels are carried forward using a ratio derived from QCEW employment data using equation 12.
| NAICS code | NAICS industry title |
|---|---|
|
513110 |
Newspaper publishers |
|
513120 |
Periodical publishers |
|
513130 |
Book publishers |
|
513190 |
Directory, mailing list, and other publishers |
|
512230 |
Music publishers |
|
516200 |
Media streaming distribution services, social networks, and other media networks and content providers |
|
519290 |
Web search portals and all other information services |
|
921140 |
Executive and legislative offices1 |
|
922190 |
Other justice, public order, and safety activities1 |
|
923110 |
Administration of education programs1 |
|
924110 |
Administration of air and water resource and solid waste management programs1 |
|
925110 |
Administration of housing programs1 |
|
926110 |
Administration of general economic programs1 |
|
927110 |
Space research and technology1 |
|
928110 |
National security1 |
|
1 Noncovered employment is calculated only for worksites owned by state and local government. |
|
![]()
where
![]()
![]()
![]()
Corporate officers represent one of the largest groups of noncovered employees. In several states, noncovered employment exists in most NAICS industries. Corporate officers and other state specific employment exemptions outside of those listed above are collected annually by CES from state labor market information offices.
Periodically, CES-N reviews states’ UI laws and refines the list of industries with noncovered employment, ensuring that CES-N captures all exempted employment within the scope of the CES survey. The program also reviews methodologies and external data sources for accuracy. Additions or changes identified during review are incorporated with the release of the following March benchmark update.
Because of the small sample in religious organizations and definitional exclusions in the collection of data for private educational services, certain ratios for these industries are recalculated with each benchmark to allow for the creation of aggregate totals. (See exhibit 13.) The series are calculated based on the weighted average of the prior year's professional and technical services, education and health services, leisure and hospitality, and other services supersectors' annual averages. For both industries, the PE and WE ratios, and, for both AE and PE, AHE and AWH are held constant through the next benchmark.
| Data type used for ratio calculation | Private educational services (65-610000) | Religious organizations (80-813100)1 |
|---|---|---|
|
Nonsupervisory-employee-to-all-employee ratio (PER) |
X | X |
|
Women-employee-to-all employee ratio (WER) |
X | |
|
Average hourly earnings (AHE) for AE and PE |
X | X |
|
Average weekly hours (AWH) for AE and PE |
X | X |
|
1 Religious organizations (80-8131000) is not published on its own; instead it is included in membership associations and organizations (80-813000). |
||
The CES-N program seasonally adjusts estimates of employment, hours, and earnings using a concurrent seasonal adjustment methodology. Many CES data users are interested in the seasonally adjusted over-the-month changes as a primary measure of overall national economic trends. Therefore, accurate seasonal adjustment is important to the usefulness of these monthly data. This section describes the CES-N seasonal adjustment methodology and software used to seasonally adjust month data.
All basic data series for employment (AE, WE, and PE) and both AE and PE hours (AWH and AWOT) and earnings (AHE) are published on a seasonally adjusted basis. Series may be seasonally adjusted by applying seasonal factors directly to the not seasonally adjusted series or indirectly through the aggregation process. The lowest level seasonally adjusted series published with first preliminary estimates are used for aggregating to higher levels. The series published after the release of first preliminary estimates are seasonally adjusted directly but are not used in aggregation. These series are noted as independently seasonally adjusted, when extracted from the LABSTAT database, because they are not used in aggregation.
The CES-N program directly seasonally adjusts most AE series at the 4-, 5-, and 6-digit NAICS level. Seasonally adjusted estimates of all employees are aggregated up either from the 3-digit NAICS or, if all 4-digit NAICS series are published with first preliminary estimates, from that level. (See exhibit 14.)
| Composite series | Component series1 | |
|---|---|---|
| CES industry code | CES industry title | |
|
10-212000 |
Coal mining | 10-212100, 10-212200, 10-212300 |
|
20-2361002 |
New single-family housing construction (except for-sale builders) | 20-236115, 20-236116, 20-236117, 20-236118 |
|
20-2362002 |
Industrial building construction | 20-236210, 20-236220 |
|
20-2380002 |
Poured concrete foundation and structure contractors | 20-238110, 20-238120, 20-238130, 20-238140, 20-238150, 20-238160, 20-238170, 20-238190, 20-238210, 20-238220, 20-238290, 20-238310, 20-238320, 20-238330, 20-238340, 20-238350, 20-238390, 20-238910, 20-238990 |
|
31-334000 |
Computer and peripheral equipment manufacturing | 31-334100, 31-334200, 31-334400, 31-334500, 31-334600 |
|
42-441000 |
Automobile dealers | 42-441100, 42-441200, 42-441300 |
|
42-449000 |
Furniture and home furnishings retailers | 42-449100, 42-449200 |
|
42-455000 |
Department stores | 42-455100, 42-455200 |
|
55-522000 |
Depository credit intermediation | 55-522100, 55-522200, 55-522300 |
|
60-540000 |
Legal services | 60-541100, 60-541200, 60-541300, 60-541400, 60-541500, 60-541600, 60-541700, 60-541800, 60-541900 |
|
60-561000 |
Office administrative services | 60-561100, 60-561200, 60-561300, 60-561400, 60-561500, 60-561600, 60-561700, 60-561900 |
|
65-621000 |
Offices of physicians | 65-621100, 65-621200, 65-621300, 65-621400, 65-621500, 65-621600, 65-621900 |
|
65-623000 |
Skilled nursing care facilities | 65-623100, 65-623200, 65-623300, 65-623900 |
|
65-624000 |
Individual and family services | 65-624100, 65-624200, 65-624300, 65-624400 |
|
1 For CES industry titles of the component series, see the CES published series webpage. 2 The component series for this industry are published with the second preliminary release. |
||
For PE series and for hours and earnings series of both PE and AE, the CES-N program seasonally adjusts directly at the 3-digit NAICS level for manufacturing industries and at the major industry sector level for all other private-sector industries. (See exhibit 7). Aggregation of these series results in indirect, higher level seasonally adjusted series.
Overtime series for both PE and AE are directly seasonally adjusted for both durable goods and nondurable goods. Overtime hours series for all of manufacturing are indirectly seasonally adjusted through aggregation.
For WE series, the CES-N seasonally adjusts directly at the major industry sector level. Higher levels up to total nonfarm are indirectly seasonally adjusted through aggregation.
The CES-N program uses X-13ARIMA-SEATS software developed by the U.S. Census Bureau to seasonally adjust monthly estimates. Seasonal adjustment models are selected annually and are based on the best fit as determined by X-13ARIMA-SEATS. Models are either additive or multiplicative and may include special adjustment for timing issues. The models remain the same until the following year’s models are selected. From month to month, new seasonal factors for the current reference month and for the prior 2 months of revised data are calculated using all relevant data up to and including the current month.
All seasonally adjusted series use either an additive or a multiplicative adjustment depending on the model that best fits the individual series. The CES-N seasonal adjustment website lists each series and whether the seasonal adjustment model is additive or multiplicative.
Seasonal adjustment of CES-N data may include model adjustments for one of two calendar-related effects.
The CES-N program refines the seasonal adjustment procedures to account for survey interval variations, sometimes referred to as the 4- versus 5-week effect. The CES survey reference period is the pay period that includes the 12th of the month. Inconsistencies often arise because either 4 or 5 weeks occur between the weeks including the 12th in a consecutive pair of months. In highly seasonal industries, these variations result in differences in the magnitude of seasonal hires or layoffs that occurred at the time the survey was taken.
BLS uses REGARIMA (regression with autocorrelated errors) modeling to identify the estimated size and significance of the calendar effect for each published series. REGARIMA combines standard regression analysis, which measures correlation among two or more variables, with ARIMA modeling, which describes and predicts the behavior of a data series based on its own history. For many economic time series, including nonfarm payroll employment, observations are autocorrelated over time; each month's value is significantly dependent on the observations that precede it. These series, therefore, usually can be successfully fit using ARIMA models. If autocorrelated time series are modeled through regression analysis alone, the measured relationships among other variables of interest may be distorted because of the influence of the autocorrelation. Thus, the REGARIMA technique is appropriate for measuring relationships among variables of interest in series that exhibit autocorrelation, such as nonfarm payroll employment.
In this application, the correlations of interest are those between employment levels in individual calendar months and the number of weeks between each month’s week including the 12th. The REGARIMA models evaluate the variation in employment levels attributable to eleven separate survey interval variables, one specified for each month, except March, because there are almost always 4 weeks between the February and March surveys. Models for individual basic series are usually fit with the most recent 10 years of data available, the standard time span used for CES-N seasonal adjustment.
The REGARIMA procedure yields regression coefficients for each of the 11 months specified in the model. These coefficients provide estimates of the strength of the relationship between employment levels and the number of weeks between surveys for the 11 modeled months. The X‑13ARIMA‑SEATS software also produces diagnostic tests of the statistical significance of the regression coefficients.
The 11 coefficients derived from the REGARIMA models provide an estimate of the magnitude of variation in employment levels associated with the length of the survey interval. These coefficients are used to adjust the CES data to remove the calendar effect. These "filtered" series are then seasonally adjusted using the standard X‑13ARIMA‑SEATS software.
The CES-N program uses a special treatment to adjust construction industry series. Accurately identifying and measuring interval effects is difficult because of the strong influence of variable weather patterns on employment movements in construction. CES-N disaggregates the construction series into regional industry estimating cells and tightens outlier designation parameters, allowing a more precise identification of weather-related outliers that can mask the interval effect and distort seasonal patterns. With these outliers removed, interval effect modeling results in a seasonally adjusted series for construction that controls for two potential distortions: unusual weather events and the 4- versus 5-week effect.
The CES-N program refines the seasonal adjustment process for hours and earnings series to correct for distortions related to the method of accounting for varying lengths of pay periods (LOPP) across months. A significant correlation occurs between over-the-month changes in both the average weekly hours (AWH) and the average hourly earnings (AHE) series and the number of weekdays in a month, resulting in noneconomic fluctuations in these series. Both AWH and AHE show more growth in short months (20 or 21 weekdays) than in long months (22 or 23 weekdays). The effect is stronger for the AWH than for the AHE series.
The LOPP calendar effect is traceable to response and processing errors associated with converting sampled respondents from providing payroll and hours data in a semi-monthly or monthly pay periods to weekly equivalents. The response error comes from sample respondents reporting a fixed number of total hours for workers regardless of the length of the reference month, while the CES conversion process assumes that the hours reporting will be variable. A constant level of hours reporting most likely occurs when employees are salaried rather than paid by the hour, as employers are less likely to keep actual detailed hours records for such employees. This causes artificial peaks in the AWH series in shorter months that are reversed in longer months.
The processing error occurs when respondents with salaried workers report hours correctly (by varying them according to the length of the month), which dictates that different conversion factors be applied to payroll and hours. The CES processing system uses the same conversion factors for hours and earnings, which are based on the number of business days in the month, resulting in peaks in the AHE series in short months and reversals in long months.
The CES-N program uses REGARIMA modeling to identify, measure, and remove the length-of-pay-period effect for seasonally adjusted average weekly hours and average hourly earnings series. The length-of-pay-period proves significant for explaining most AWH and AHE movements in private service-providing industries, except utilities, in mining and logging and in some manufacturing industries. For this reason, calculations of over-the-year changes in the establishment hours and earnings series should use seasonally adjusted data.
The series to which the length-of-pay-period adjustment is applied are not subject to the 4- versus 5-week adjustment, as the modeling cannot support the number of variables that would be required in the regression equation to make both adjustments.
A special adjustment is made in November to account for variations in employment due to the presence or absence of poll workers in local government, excluding educational services. This procedure minimizes fluctuations in seasonally adjusted data in local government, excluding education employment series that occur with short-term hiring of poll workers in years with congressional and presidential elections.
The effect of poll workers on employment is not a true seasonal effect because it occurs only once every 2 years in November. The adjustment procedure is accomplished through X-13ARIMA-SEATS by removing an estimate of the number of poll workers in the series prior to seasonal adjustment in order to prevent November spikes in total nonfarm employment that result from the 1-day employment of thousands of poll workers.
Two holidays—Good Friday (Easter) and Labor Day—do not occur on the same date every year and may or may not fall during the survey reference period—the pay period including the 12th of the month. The presence or absence of one of these holidays in the survey reference period may result in significant variation in some average weekly hours and average weekly overtime hours series with fewer hours occurring when the holiday occurs during the week of the 12th. The floating holiday adjustment is accomplished through the REGARIMA option within the X-13ARIMA-SEATS procedure. A regression model estimate of the significance of the presence or absence of the holiday during the week of the 12th is made, using a dummy variable to indicate in which years the holiday is present or absent. For industry series where the dummy variable test is significant, an adjustment is made to the original series before it is input into the seasonal adjustment procedure using the estimated regression parameters. The special adjustment procedure identifies the magnitude of the effect and adjusts for it prior to seasonally adjusting the series, thereby neutralizing the effect.
The CES-N program produces and publishes employment series for residential specialty trade contractors (20-238001) and nonresidential specialty trade contractors (20-238002). These series are derived independently from the 3-digit NAICS series specialty trade contractors (20-238000). A raking procedure ensures that the sum of the seasonally adjusted residential specialty trade contractors and seasonally adjusted nonresidential specialty trade contractors series equals employment of seasonally adjusted specialty trade contractors.
The raking procedure begins by directly seasonally adjusting the residential and nonresidential series at the 3-digit NAICS level and summing them to get a total. Ratios of seasonally adjusted residential-to-total employment and seasonally adjusted nonresidential-to-total employment are calculated. These ratios are then multiplied by employment of the official 3-digit seasonally adjusted specialty trade contractors all employees estimate to obtain seasonally adjusted estimates of official residential and nonresidential specialty trade contractors.
Derivative series, plus annual and quarterly averages, are data derived from sample-based estimates. All hours and earnings derivative data are produced for all employees (AE) and production and nonsupervisory employees (PE) using their respective sample-based employment, hours, and earnings estimates. The following equations describe how derivative data are calculated.
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Annual averages of average weekly earnings are the product of the annual averages of AWH and AHE.
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
Annual averages for real earnings use annual averages for AWE, AHE, and CPIs in equation 15.
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The production and nonsupervisory employees-to-all employees ratio (PER) uses the same formula as WER, substituting in the PE estimate for WE.
Diffusion indexes are produced for total private and for manufacturing using all employee estimates at the 4-digit NAICS level. If the lowest level published is at the 3-digit level, then that 3-digit NAICS is used. Seasonally adjusted data are used for diffusion indexes over a 1-, 3-, and 6-month time span, while not seasonally adjusted data are used for 12-month spans. Lists of industries in the diffusion index calculations are available in the CES diffusion index series spreadsheet.
To derive the indexes, calculate the employment change for the 1-, 3-, 6-, or 12-month span for each component industry. Assign a value of 0 to each employment decrease, 50 to each unchanged observation, and 100 to each employment increase over the selected time span. The diffusion index is the average (mean) of the assigned values.
The CES survey—like other sample surveys—is subject to two types of error: sampling and nonsampling error. The magnitude of sampling error, or variance, is directly related to the size of the sample and the percentage of universe coverage achieved by the sample. The CES sample covers over one-third of total universe employment, yielding a very small variance for the total nonfarm estimates. Nonsampling error includes response errors, nonresponse bias, and frame imperfections, such as the inability to account for business births.
The sum of sampling and nonsampling errors represents total survey error. Unlike most sample surveys that publish sampling error as their only measure of error, CES-N derives an annual approximation of total error using lagged and independently derived universe data. While the benchmark error is often used as a proxy measure of total error for the CES survey estimate, it represents the difference between two employment estimates calculated from separate statistical processes—the CES sample process and the unemployment insurance administrative process. Therefore, it reflects the net of errors present in each program. Historically, the benchmark revision has been small for total nonfarm employment. See the earlier discussion on benchmarks for more information related to the CES annual benchmark process.
The CES sampling error, or sampling variance, for a given benchmark year applies to all private industry and total nonfarm estimates from the most recent March benchmark to the current month's estimate. The errors are calculated as average values of the observed median monthly error estimates over the latest 3 years. The CES-N program publishes first preliminary estimates of employment, hours, and earnings based on less than the total sample. Revised sample-based estimates are published during the 2 subsequent months to allow for receipt of additional sample.
Measures of sampling variability, in the form of standard and relative-standard errors, are available on the CES-N variance webpages. (See all employees (AE) and their respective hours and earnings, production and nonsupervisory employees (PE) and their respective hours and earnings, and women employees (WE).) Sampling errors for the third release of estimates are very similar to those for the second release and are available upon request. See the Revisions between over-the-month estimates, 1979-present page for more information related to revisions to monthly, sample-based estimates.
The estimation of sample variance for CES-N estimates is accomplished through Fay’s method of balanced half samples (BHS). Using Fay’s BHS method, the sample is repeatedly divided into halves systematically. For each replicate division, the original sample weights are adjusted in both halves of the sample: weights for units that belong to one half of the sample are multiplied by a factor of 1+γ, whereas weights for units in the other half of the sample are multiplied by a factor of 1−γ. Replicate estimates based on these adjusted weights are calculated using the same estimation formula as used for the full-sample estimate. The procedure is repeated k times. The sample variance is calculated by measuring the variability of the replicate estimates as shown in equation 27.
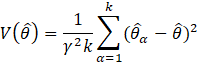
where
![]()
![]()
![]()
Variance statistics are useful for comparison purposes, but they do have some limitations. Variances reflect the error components of estimates that are due to surveying only a subset of the population, rather than conducting a complete count of the entire population; they do not reflect nonsampling error, such as response errors and bias due to nonresponse. Sampling variances (or sampling errors) of the over-the-month change in estimates are useful in determining when changes are significant at some level of confidence.
Standard error tables provide a reference for relative standard errors of all major series developed by the CES-N program. The sampling error tables are presented as relative standard errors (rse) that are derived as the standard error divided by the level estimate (Y) and expressed as a percent. Multiplying the relative standard error by its estimated level value gives the estimate of the standard error:
![]()
For example, suppose that the level of AE for an industry is estimated at 8,500,000 with the first release of estimates for a given month, and the series has an approximate relative standard error of 0.4 percent at the first release. A 90-percent confidence interval would then be the interval:
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
Standard error tables provide a reference for the standard errors of 1-, 3-, and 12-month changes in CES-N employment, hours, and earnings series. The errors are presented as standard errors of the changes. The standard and relative standard errors are appropriate for use with both seasonally adjusted and not seasonally adjusted CES data. Suppose that the over-the-month change in average hourly earnings (AHE) from one month to the next is $0.30, and the standard error for a 1-month change is $0.25. One can say that the true estimate of over-the-month change, based on a 90-percent confidence interval, is included in the following interval:
$0.30 ± (1.645 × $0.25)
= $0.30 ± $0.41
= -$0.11 to $0.71
Because the interval -$0.11 to $0.71 includes $0.00, the change in average hourly earnings is not statistically different from 0 for that month.