U.S. flag

An official website of the United States government

Department of Labor Logo United States Department of Labor
Dot gov

The .gov means it's official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Productivity
Bureau of Labor Statistics > Productivity > Publications > Articles and Research

Dispersion Statistics on Productivity

A Joint Project

BLS emblem census bureau logo

 

How does productivity vary by establishment?

On September 12, 2024, the Bureau of Labor Statistics (BLS) and the U.S. Census Bureau updated an experimental data product, Dispersion Statistics on Productivity (DiSP). The first release of DiSP was in 2019. DiSP covers all 86 4-digit North American Industry Classification System (NAICS) manufacturing industries for the years 1987 through 2021. Industry classifications conform to the NAICS 2012 structure. Detailed information on the construction of this data product is available in the working paper, "Dispersion in Dispersion: Measuring Establishment-Level Differences in Productivity," which was published in the Review of Income and Wealth.

On This Page:

A peek at the patterns underlying industry productivity

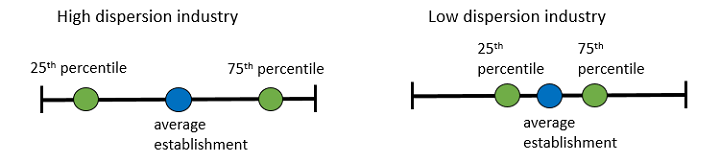
Some industries have a wider spread, or dispersion, than others between more productive establishments and less productive establishments. This has important implications for how productivity (the ratio of outputs to inputs) changes in the industry as a whole over time. The official industry productivity statistics published by BLS are, after all, the weighted average productivity of all the establishments that make up the industry.

You may have a picture in your mind of how a certain industry’s productivity distribution looks. Are some establishments rising stars of productivity, leaping far above average during times of rapid change, while others struggle to improve productivity? These dynamics lead to a widening distribution. Do most establishments tend to rise and fall together with the business cycle? This pattern might suggest a compressed or stable distribution of productivity.

comparison of a high dispersion industry and low dispersion industry on a box and whisker plot showing the 25th percentile, average establishment, and 75th percentile. The low dispersion is much closer together.

 

DiSP provides statistics on establishment-level distributions of real gross output per hour worked and total factor productivity (gross output per unit of combined inputs). The primary data sources include microdata from the Census Bureau's Annual Survey of Manufactures (ASM), Census of Manufactures (CM), and Longitudinal Business Database (LBD). We also use industry-level data from the BLS Current Population Survey (CPS). To improve our understanding of productivity distributions within industries, DiSP includes an array of summary statistics: standard deviations, interquartile ranges (comparing productivity at the 75th and 25th percentiles), and interdecile ranges (comparing productivity at the 90th and 10th percentiles) of the within-industry distributions of establishment-level productivity levels. DiSP also presents comparisons between the 10th and 1st percentiles and between the 90th and 99th percentiles of within-industry distributions of establishment-level productivity levels. All sample data are frequency weighted. Furthermore, the data set includes activity-weighted versions of these dispersion measures where the weights are based upon the denominator of the relevant productivity measure. As an example, for output per hour worked, the activity weights are defined by hours shares.

BLS and the Census Bureau welcome feedback. In addition, restricted-use microdata are available for qualified researchers on approved projects in the Federal Statistical Research Data Centers (FSRDC).

Note: for measures of spatial variation in productivity, please see BLS measures of state productivity.

Back to Index Back to Index

What are productivity dispersion statistics?

DiSP differs in substantial ways from other BLS series of labor productivity in 4-digit NAICS manufacturing industries. These diagrams summarize the basic differences in source data, methodology, and the end products.

Dispersion Statistics on Productivity

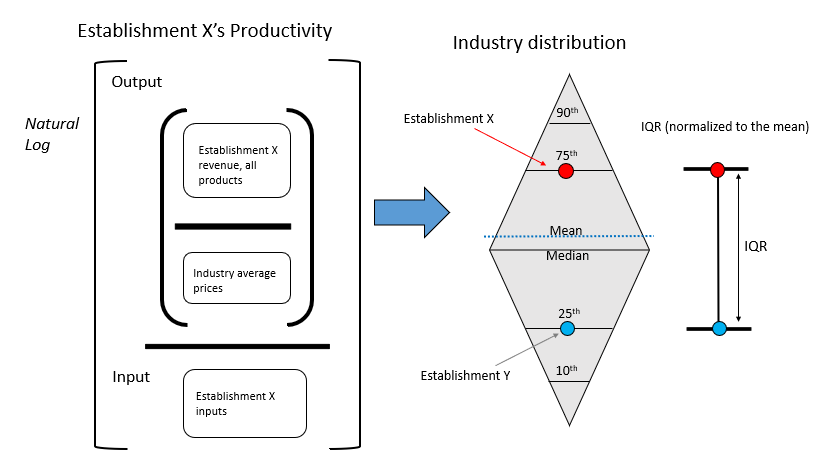
For dispersion statistics, we first calculate an establishment’s productivity as revenues (adjusted for price change) per unit of input. The input unit could be hours worked (for gross output productivity measures) or all factor input costs (for our total factor productivity measures). We then take natural logarithms of establishment productivity and subtract the average productivity in its 4-digit industry to get a roughly zero-centered normal distribution around the industry's average productivity.

In the simplified illustration below, we rank the productivity levels of all establishments in an industry in a given year and determine that Establishment X is at the 75th percentile of the productivity distribution. Another establishment Y happens to fall at the 25th percentile of this industry's productivity distribution. The distance between establishments X and Y — i.e., the difference of the log-productivity levels, after normalizing to the industry mean — is the interquartile range (IQR). Since ln(x)-ln(y) is equivalent to ln(x/y), another way to view the IQR is as the approximate interquartile ratio. Taking the exponential of our published log-form IQR statistics, exp(ln(x/y)) is the same as x/y, after accounting for rounding error.

(Note: the weighted mean productivity level of the industry could be higher or lower than that of the median establishment.)

Graphic of Establishment X's Productivity feeding industry distribution

 

Official BLS Productivity Statistics for Detailed Manufacturing Industries

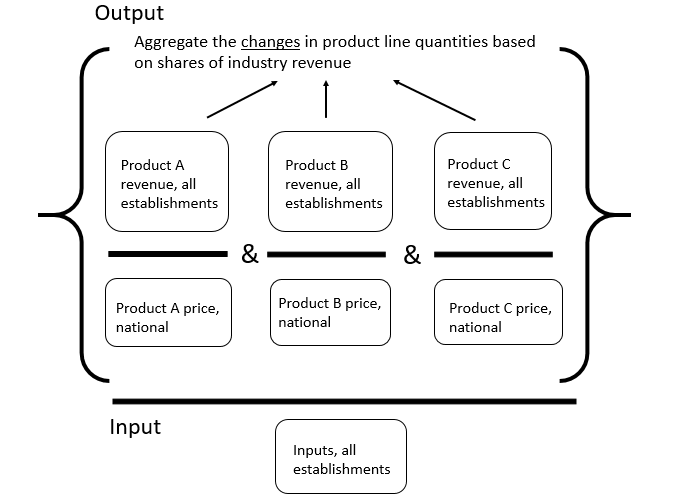
Rather than aggregating up from the microdata, BLS's official industry productivity statistics use revenues from the published data sets of the CM and ASM which have already been aggregated. Hours worked are calculated from BLS sources, not the ASM. Capital services and intermediate inputs data, used in total factor productivity measures, are derived from published data tables provided mainly by the Bureau of Economic Analysis and the Census Bureau.

Graphic showing Output over Input. Output aggregates the changes in product line quantities based on shares of industry revenue for all establishments. Input is the inputs of all establishments.

 

Back to Index Back to Index

Summary Charts of Manufacturing Industries

Labor Productivity, 1987–2021

Gross output per hour worked is the productivity dispersion measure closest to the official BLS measure of industry labor productivity, which is sectoral output per hour worked. (See how these measures differ from other BLS productivity statistics.)

While productivity levels of establishments vary within a NAICS-defined industry (within-industry dispersion), this measure of variance differs from industry to industry (between-industry “dispersion in dispersion”). Let’s look at productivity dispersion at the level of the manufacturing sector (NAICS 31-33), which comprises 86 4-digit NAICS industries. We consider the full 1987–2021 period in our data sets.

Line chart of labor productivity dispersion by industry (unweighted IQRs)
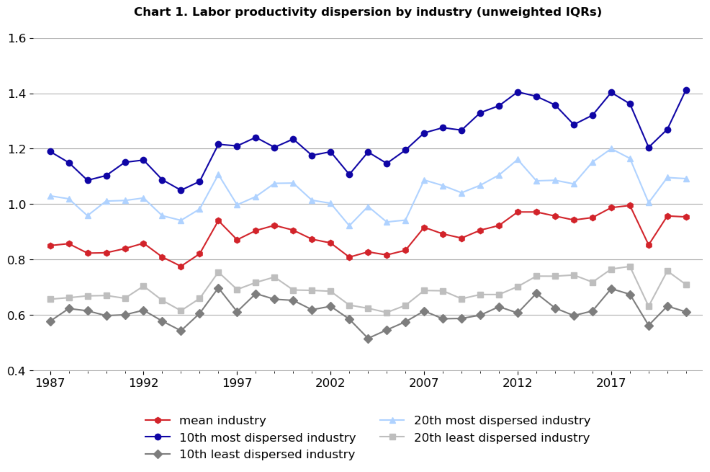
Chart 1 data. Labor productivity dispersion by industry (unweighted IQRs)

 

Chart 1 shows the distribution, at the manufacturing sector-level, of the industry dispersions of gross output per hour worked. Within-industry dispersion is defined here as the interquartile range (IQR) of establishments’ log-productivity levels. The line for “mean” represents the average within-industry dispersion for all 86 manufacturing industries. In 2021, the mean IQR was about 0.95, which means that in the average industry, establishments at the 75th percentile of the average industry's productivity distribution were about e 0.95 ~ 2.6 times as productive as establishments at the 25th percentile. The industries that rank as 10th most (or least) dispersed are not necessarily the same industries from one year to the next. Rather, they are the industries that have the 10th highest (or lowest) IQR out of the 86 industries for each particular year. The same is true for the 20th most/least dispersed industries.

Be careful about reading too much into the dips and rises of these trend lines over short periods. Because establishments rotate in and out of the ASM sample panels, it is possible that some of this volatility comes from changes in composition. Since establishments are not weighted by hours shares (a.k.a. relative size) in this chart, much of the variance may be explained by the smaller establishments.

Line chart of labor productivity dispersion by indsutry (weighted IQRs) 1987-2021
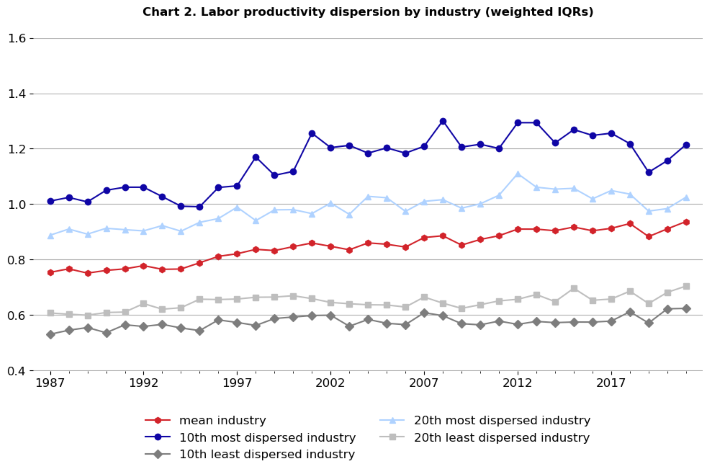
Chart 2 data. Labor productivity dispersion by industry (weighted IQRs)

 

For chart 2, establishments are weighted by their shares of their industry’s total hours worked. This reduces the volatility and compresses the upper part of the distribution. Also, it is easier to see now that the mean IQR of all industries rose over time, driven mainly by an increase in the IQR of the industries with greater dispersion.

Total Factor Productivity, 1987–2021

Charts 3 and 4 display distributions of industries by total factor productivity (TFP) dispersion, using the same rankings as reference points for between-industry dispersion. For chart 4, establishments are weighted by their composite input shares. The measure of within-industry dispersion in both charts is, again, the IQR.

Line chart of TFP dispersion by industry (unweighted IQRs) 1987-2021
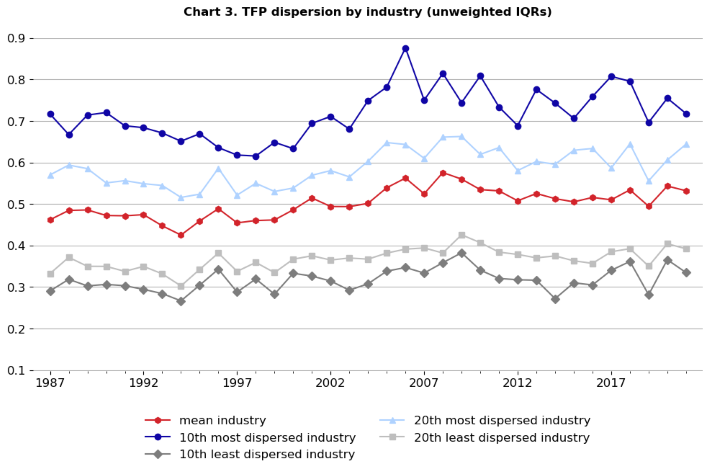
Chart 3 data. TFP dispersion by industry (unweighted IQRs)

 

For both charts 3 (unweighted) and 4 (weighted), note the contraction in the vertical axis scale; there is less within-industry dispersion in TFP than in gross output per hour worked. One similarity between the TFP dispersion charts and the labor productivity dispersion charts is that the mean IQR rose between 1987 and 2021.

Line chart of TFP productivity dispersion by industry (weighted IQRs) 1987-2021
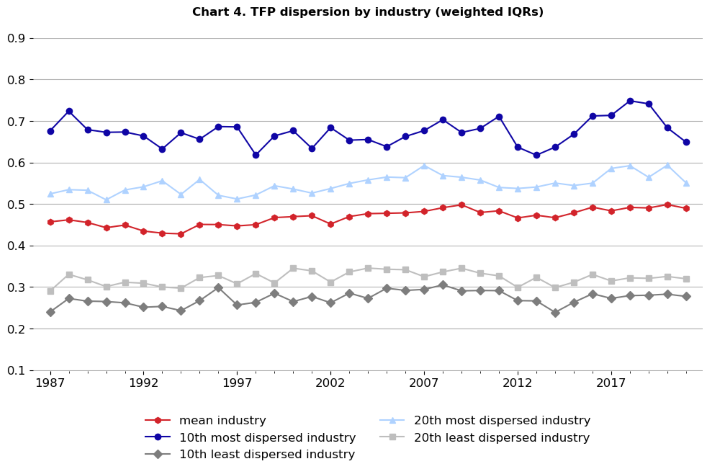
Chart 4 data. TFP dispersion by industry (weighted IQRs)

 

Comparing chart 4 to chart 3 reveals that (like the first two charts) there is less between-industry dispersion of IQRs when the establishments are weighted by combined input shares.

Comparison of High and Low Dispersion Industries

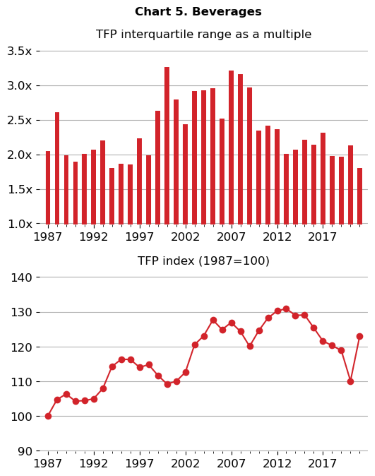
One goal of the DiSP project is to better understand the relationship between productivity dispersion within an industry and the industry’s overall productivity trend. Here are a pair of examples (charts 5 and 6) from the TFP dispersion statistics (unweighted establishment distributions) that compare the interquartile range to the BLS TFP index for the whole industry. NAICS 3121, beverages manufacturing (chart 5), had one of the highest IQRs on average over the 1987-2021 period. This industry comprises establishments producing soft drinks, bottled water, ice, beer, wine, and spirits. NAICS 3362, motor vehicle body and trailer manufacturing (chart 6), had one of the lowest IQRs on average. This industry produces motor vehicle bodies, truck trailers, motor homes, and travel trailers and campers.

Bar chart of total factor productivity interquartile range as a multiple for the beverages industry, 1987-2021 on top of a line chart of the total factor productivity index of the same time period with base year of 1987 Bar chart of TFP interquartile range as a multiple for motor vehicle bodies and trailers industry from 1987 to 2021, on top of a line chart of the same years or the TFP index, base year 1987
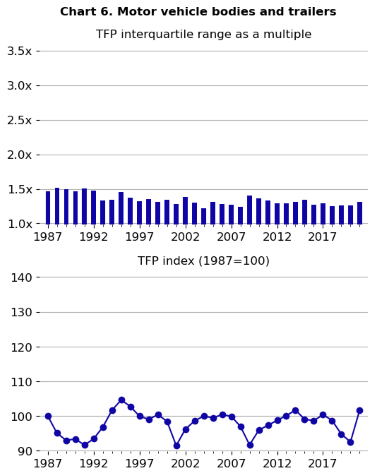
Charts 5 and 6 data. Comparison of high and low dispersion industries

 

For the upper panels of charts 5 and 6, we present the interquartile ranges as approximate ratios of productivity levels, allowing for a more tangible illustration of how productive the 75th percentile establishments are relative to the 25th percentile establishments. The lower panels display overall TFP indexes from the official BLS industry productivity series.

Charts 5 and 6 show that the beverages industry has larger and more volatile IQR values from 1987 to 2021 compared to motor vehicle bodies and trailers. Additionally, TFP for beverages grows from 1987 to 2021, whereas TFP stays relatively steady for motor vehicle bodies and trailers.

Publications using DiSP data

The following studies are examples of how DiSP data are being used for research. The studies below include published articles, working papers, and reports. This list is not comprehensive. If you have authored a study using DiSP data and would like to include it in this list, please contact the BLS Productivity Program.

Key questions and answers

Why are BLS and the Census Bureau publishing these measures?

Understanding more about variation in productivity within industries can better help us understand variation in productivity levels and change between industries. Better knowledge of industry productivity, in turn, can help us better understand productivity in the higher-level aggregates, like the manufacturing or nonfarm business sectors.

Productivity growth and employee compensation are related at the establishment level: highly productive establishments tend to be high-wage establishments. Therefore, differences in productivity dispersion could be related to the distributions of wages and income.

Back to Index Back to Index

How are these measures different from other BLS productivity statistics?

Dispersion statistics are a new way of looking at productivity in official U.S. economic statistics. While the BLS Office of Productivity and Technology publishes official measures of productivity for major sectors and detailed industries, this joint BLS-Census product differs in some fundamental ways:

  • A focus on variation within industries rather than industry aggregate averages. The degree to which individual establishments differ from the average is more relevant, to DiSP, than the average itself. Therefore, industry productivity averages are normalized to make it easier to compare distributions.
  • More attention to productivity levels than time series. Again, the purpose here is not to compare which industries show the highest levels of productivity, but to study the within-industry distributions. Nonetheless, there are observable time series trends in the DiSP data, such as that dispersion generally rose during the Great Recession but fell during the recession that followed the dot-com bust.
  • For the dispersion statistics on gross output per hour worked and total factor productivity, the output series are based on a gross output concept. The official BLS industry productivity statistics use a sectoral output concept. The ASM does not track who products are sold to, or which industries they came from, so it is not possible to remove intrasectoral shipments from DiSP output calculations. (A Monthly Labor Review article explains the importance of intrasectoral measurements in industry productivity series.)
  • DiSP data on output and hours worked, aggregated from ASM establishment data up to the industry level, correlate well with BLS official industry-level measures. (This is despite BLS using BLS sources, rather than the ASM, for the hours worked data.)

Please see the BLS Handbook of Methods for an overview of data sources and methodology in the official industry productivity statistics.

Back to Index Back to Index

What interesting patterns have researchers found so far?

  • There are large differences in productivity across establishments within industries. On average, over the period, an establishment at the 75th percentile of the labor productivity distribution is more than twice as productive as an establishment at the 25th percentile of the distribution.
  • Dispersion is significant in the tails of the productivity distributions. That is, establishments’ productivity levels vary, relative to each other, when we look at groups of the most productive or least productive establishments in an industry.
  • Dispersion in productivity has increased between 1997 and 2021.
  • Most of the within-industry dispersion in productivity is not accounted for by standard establishment characteristics like business size, age, or location.

Back to Index Back to Index

Why do the productivity dispersion data for manufacturing industries cover fewer years than the total factor productivity data?

The Census Bureau's Longitudinal Business Database (LBD) provides establishment level data used to calculate dispersion statistics. The LBD becomes available approximately nine months after the Annual Survey of Manufactures (ASM), which is the primary source for total factor productivity data at the industry level. For this reason, the dispersion statistics are published with a one-year lag after the total factor productivity series.

Back to Index Back to Index

How will BLS and the Census Bureau expand and improve this data product?

BLS and the Census Bureau are exploring ways to expand the coverage to the retail trade sector.

Back to Index Back to Index

Last Modified Date: September 12, 2024